分数阶BAM神经网络的全局渐进稳定性
李 倩,李 东,王 娴
(重庆大学 数学与统计学院,重庆 401331)
分数阶BAM神经网络的全局渐进稳定性
李 倩,李 东,王 娴
(重庆大学 数学与统计学院,重庆 401331)
研究了分数阶BAM神经网络平衡点的唯一存在性和全局渐近稳定性,利用压缩映像原理得到了系统平衡点唯一存在的充分条件;通过构造Lyapunov函数,运用Lyapunov函数理论、矩阵不等式法和Laplace积分变换法,得到了所研究模型平衡点的全局渐进稳定的充分条件,以矩阵不等式的形式给出了更为严格和更易验证的条件,并通过数值仿真验证了结论的正确性。
分数阶;BAM神经网络;压缩映像原理;矩阵不等式;Laplace积分变换
双层双向联想记忆(Bidirectional Associative Memory,BAM)神经网络[1]是单层Hopfield型神经网络的延拓,其特有的双向交互传递机制使得神经网络具有自学习和双向联想储存功能,因此在模式识别、图像处理和优化问题等方面广泛应用。BAM神经网络的稳定性是研究神经网络系统的前提,文献[2-4]利用压缩映像原理和Lyapunov稳定理论得到了具有离散定常时滞的BAM神经网络平衡点唯一存在和全局指数稳定的充分条件;文献[5]运用同胚映射和Lyapunov方法研究了相同课题;文献[6]用微分不等式和矩阵理论对一类具有变时滞脉冲BAM神经网络解的存在性和唯一性进行了研究,得到了平衡点处的全局指数稳定性;文献[7]使用Lyapunov稳定理论和延迟分区法来研究具有Markovian跳跃参数的BAM神经网络的稳定性;基于矩阵不等式法和固定点定理;文献[8]得到了一类具有时滞的Cohen-Grossberg BAM神经网络的全局指数稳定的充分条件。但以上研究都是基于经典的整数阶数学模型,容易陷入局部稳定,使得实验结果无法精确地反映实际模型全局的状态。
为克服整数阶模型的缺点,分数阶微积分被引入到神经网络的研究之中[9-11]。分数阶神经网络的优势是可学习和自适应未知或不确定系统,能够并行分布处理大量的运算,利用较少历史数据可以充分地逼近任意复杂非线性系统,其研究更具实际意义[12-14]。
基于整数阶BAM神经网络和分数阶微积分的成熟的理论研究,通过构造分数阶BAM神经网络模型,利用压缩映像原理对系统平衡点的唯一存在性进行了分析,接着构造适合的Lyapunov函数,结合Caputo导数的性质、Lyapunov函数理论矩阵不等式法和Laplace积分变换法得到该系统稳定点的全局渐进稳定的充分条件。证明过程削弱了整数阶系统稳定的限制条件,并给出全局渐进稳定的矩阵不等式条件,推广并改进了相关文献的证明,最后通过数值仿真验证了结论的有效性。
1 模型和预备知识
考虑如下形式的分数阶BAM神经网络模型:
(1)
其中,xi(t),yj(t)(i=1,2…n,j=1,2,…m)表示BAM神经网络神经元的两层状态变量,ai>0,cj>0表示两层神经元的自反馈系数,bij,dij表示两层神经元之间的互联系数,Ii,Jj表示外部恒定输入,fj(·),gi(·)表示两层神经元之间的激励函数。这里假设fj(·),gi(·)满足全局Lipschitz条件,且fj(0)=0,gi(0)=0,即存在Lipschitz常数lj≥0,mi≥0,使得
(2)
系统(1)的初值条件为
(3)
定义1 (Caputo型分数阶导数)如果f(t)∈C1(0,+∞),那么称
(4)
为函数f(t)的α阶Caputo型分数阶导数。其中Γ(·)为Gamma函数。
Caputo型分数阶导数的Laplace变换为
(5)
其中,F(s)=L{f(t)},当m=1时,则有L{CDαf(t)}==sαF(s)-sα-1f(0)。
定义2 Mittag-Leffler函数的单参数和双参数定义分别为
(6)
当β=1时,Eα(z)=Eα,1(z)。
Mittag-Leffler函数Laplace变换为
(7)

引理1[15]Caputo导数CDα具有如下性质:
(8)
式(8)中,a,b,c为常数。
引理2[16]可微向量x(t)∈Rn,则对任意时间t≥t0,都有
∀α∈(0,1)
(9)
引理3 (压缩映像原理)设(Χ,d)是一个完备度量空间,Τ是Χ上的一个压缩映射,则Τ有唯一的不动点。
2 主要结果
首先分析分数阶BAM神经网络平衡点的存在性和唯一性。

假设系统(1)的平衡点存在,则平衡点满足方程组:
(10)
令μi(t)=aixi(t),νj(t)=cjyj(t),代入(10)整理得到
(11)
定义映射φ:Rn+m→Rn+m,其中φ=(φ1,…φn,φn+1,…,φn+m)T,

(12)
由于系统(1)的激励函数满足全局Lipschitz条件,则对映射φ有
(13)

由定理1和系统(1)的参数条件可得:0 基于定理1,证明系统(1)在平衡点处的全局渐进稳定性。先对系统(1)进行向量形式变换: (14) F(y(t))=(f1(y1(t)),…,fm(ym(t))))T, G(x(t))=(g1(x1(t)),…,gn(xn(t)))T, I=(I1,…In)T,J=(J1,…Jm)T。 (15) (16) 初值条件的向量表示形式为 (17) 因此,研究分数阶BAM神经网络模型(14)在平衡点(x*,y*)T处的全局渐进稳定性,只需要研究平移系统(16)在平衡点(0,0)T的全局渐进稳定性即可。 (18) 将系统(16)代入式(11)中,得到 (19) (20) 令δ=-2λ>0,则CDαV(t)≤-δV(t),则存在非负函数K(t),使得 CDαV(t)+K(t)=-δV(t) (21) 对式(21)两端进行Laplace变换得到 sαΜ(s)-sα-1V(0)+Ν(s)=-δΜ(s) (22) 其中,M(s)=L{V(t)},Ν(s)=L{K(t)},式(22)整理得到 (23) 对式(23)两端作Laplace逆变换,则 V(t)=V(0)Eα(-δtα)-K(t)*[tα-1Eα,α(-δtα)] (24) V(t)≤V(0)Eα(-δtα) (25) 这里, (26) 下面具体分析有4个神经元的分数阶BAM神经网络在平衡点处的稳定性。 例 考虑X层和Y层各有2个神经元的分数阶BAM神经网络模型。 在平衡点处作平移变换,得到系统(16)的各参数矩阵为 给定初值条件(8,9,10,8)T,MATLAB编程得到该模型的4个神经元在平衡点处的稳定过程(如图1—4所示)。 从图1—4可看出,在给定初值条件下,4个神经元能在短时间内就能实现稳定,且数值模拟最终得到的4个神经元的平衡点和理论计算出的平衡点基本完全重合,因此,可说明得出的结论是有效的。 图1 x1收敛曲线Fig.1 x1 convergence curve 图2 x2收敛曲线Fig.2 x2 convergence curve 图3 y1收敛曲线Fig.3 y1 convergence curve 图4 y2收敛曲线Fig.4 y2 convergence curve 在激励函数满足全局Lipschitz条件下,利用压缩映像原理得到了一类常系数分数阶BAM神经网络模型平衡点唯一存在的充分条件,运用定理1的结论可以更高效地判断系统(1)的平衡点是否存在。定理2以矩阵不等式的形式给出了模型在平衡点处的全局渐进稳定的条件,证明减弱了相关对模型参数的限制,其结论更易验证。但考虑构造Lyapunov函数的困难,未来可结合整数阶BAM神经网络分数阶微积分的其他研究成果,对具有定常时滞、时变时滞和脉冲的分数阶BAM神经网络的稳定性进行分析和控制。 [1] KOSKO B.Bidirectional Associative Memories[J].IEEE Transaction on Systems Man Cybernetics,SMC-18,1988,18:49-60[2] CAO J D.Global Asymptotic Stability of Delayed Bidirectional Associative Memory Neural Networks[J].Applied Mathematics & Computation,2003,142(2-3):333-339 [3] LI Y K.Global Exponential Stability of BAM Neural Networks with Delays and Impulses [J].Chaos Solitons & Fractals,2005,24(1):279-285 [4] HUANG Z K,XIA Y H.Global Exponential Stability of BAM Neural Networks with Transmission Delays and Nonlinear Impulses[J].Chaos Solitons & Fractals,2008,38(2):489-498 [5] YANG D G,LIAO X F,HU C Y,et al.New Delay-dependent Exponential Stability Criteria of BAM Neural Networks with Time Delays[J].Mathematics & Computers in Simulation,2009,79(5):1679-1697 [6] LI K L.Delay-dependent Stability Analysis for Impulsive BAM Neural Networks with Time-varying Delays[J].Computers & Mathematics with Applications,2008,56(8):2088-2099 [7] LIU H Y,OU Y,HUA J,et al.Delay-dependent Stability Analysis for Continuous-time BAM Neural Networks with Markovian Jumping Parameters[J].Neural Networks the Official Journal of the International Neural Network Society,2010,23(23):315-321 [8] XIANG H J,WANG J H,CAO J D.Almost Periodic Solution to Cohen-Grossberg-type BAM Networks with Distributed Delays[J].Neurocomputing,2009,72(16-18):3751-3759 [9] YANG X J,LI C D,SONG Q K,et al.Mittag-Leffler Stability Analysis on Variable-time Impulsive Fractional-order Neural Networks[J].Neurocomputing,2016,207:276-286 [10] CHEN L P,WU RC,CAO J D,et al.Stability and Synchronization of Memristor-based Fractional-order Delayed Neural Networks[J].Neural Networks,2015,71(C):37-44 [11] Rakkiyappan R,Velmurugan G,CAO J D.Stability Analysis of Fractional-order Complex-valued Neural Networks with Time Delays [J].Chaos Solitons & Fractals,2015,78(1):297-316 [12] 张小红,俞梁华.分数阶细胞神经网络自适应同步控制设计及电路仿真[J].控制理论与应用,2016,33(6) ZHANG X H,YU L H.Fractional-order Cellular Neural Networks Adaptive Synchronization Control Circuit Design and Simulation[J].Control Theory and Applications,2016,33(6) [13] 李昕,邢丽坤.基于最优阶次分数阶神经网络的交通流预测[J].计算机工程与应用,2012,48(18):226-230 LI X,XING L K.Traffic Flow Forecast Based on Optimal Order Fractional Neural Networks[J].Computer Engineering and Application,2012,48(18):226-230 [14] 付华,王福娇,陈子春.基于分数阶神经网络的瓦斯涌出量预测[J].传感器与微系统,2013,32(5):31-34 FU H,WANG F J,CHEN Z C.Prediction of Gas Emission Quantity Based on Fractional Order Neural Network[J].Transducer and Microsystem Technologies,2013,32(5):31-34 [15] PODLUBNYI.Fractional Differential Equtions:an Introduction to Fractional Derivatives,Fractional Diffrerential Equations,to Methods of Their Solution and Some of Their Application[M].New York:Academic Press,1998 [16] AGUILA-CAMACHO N,DUARTE-MERMOUD M A,GALLEGOS J A.Lyapunov Functions for Fractional Order Systems[J].Communications in Nonlinear Science & Numerical Simulation,2014,19(9):2951-2957 责任编辑:罗姗姗 Global Asymptotic Stability of Fractional-order BAM Neural Networks LI Qian, LI Dong, WANG Xian (School of Mathematics and Statistics, Chongqing University, Chongqing 401331, China) This paper studies the unique existence and global asymptotic stability of the equilibrium point of fractional-order BAM neural networks, obtains the sufficient condition for the unique existence of the systematic equilibrium point by using contraction mapping principle, receives the sufficient condition of the global asymptotic stability of the equilibrium point of the studied model by constructing Lyapunov function and by using Lyapunov function theory, matrix inequality method and Laplace integral transform method, gives more strict and easier verification condition by the form of matrix inequalities and verifies the correctness of the conclusion by numerical simulation. fractional-order; BAM neural network; contraction mapping principle; matrix inequality; Laplace integral transform 10.16055/j.issn.1672-058X.2017.0001.005 2016-09-04; 2016-10-10. 李倩(1991-),女,重庆合川人,硕士研究生,从事动力系统、神经网络稳定性研究. 0175.1 A 1672-058X(2017)01-0021-06


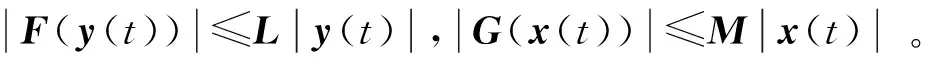



3 数值模拟









4 结语和展望

