思维拔节：实现数学价值与学力生长融合的纽带

【摘要】数学学科的核心价值在于发展学生的思维能力，而思维能力是学力的核心成分。思维能力的培养是发掘数学学科价值和发展学生学力融合的纽带。选择挑战性的学习材料、设计参考性的教学问题和组织主体性的探究活动，引领学生的思维拔节，可以让学生感悟数学学科价值，发展综合学力，实现生命成长。

【关键词】思维；数学价值；学力；学习材料

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2016）44-0035-02

【作者简介】沈军，南京市中华中学附属小学（南京，210000），一级教师，南京市建邺区数学学科带头人。

在当今社会中，学习能力是学生适应社会发展与实现个体可持续发展的核心素养。其中，思维能力是学生学习能力的核心。从这个角度说，聚焦思维能力培养，实现思维的拔节和学力的提升，自然就成为融合发掘数学学科价值和发展学生学力的纽带。下面笔者以自主开发的数学综合实践课《对称与等分》的教学为例，谈一谈思维拔节的有效举措。

一、精心选择挑战性的学习材料——实现思维拔节的前提

学习材料是学生解决数学问题、获得数学知识、提高数学能力的基本载体，也是学生体验数学价值，形成正确数学观的重要资源。学习材料主要包括教材中的课程资源与教材外拓展的课程资源。如果学习材料脱离学生的已有知识经验，高于普遍学力，学生“跳起来摘不到果子”，缺少成功的体验，就没有思维的欲望和思维拔节的可能。因为只有学习材料具有一定的挑战性，学生的思维才会被激活。这就要求教师在选择学习材料时，要把它落在学生的“最近发展区”，同时铺设台阶引领学生拾级而上，这样才能实现思维的拔节。本节课学习材料设计分为三个层次。

层次一：研究单个基本图形的对称与等分。先从圆开始，然后到正方形和长方形，再到平行四边形。

层次二：研究两个基本图形组成的组合图形的对称与等分。先出示一个圆和一个正方形组成的轴对称图形（如图1）。随着圆不停地滚动，圆的位置发生了变化，组合图形也从最初的轴对称图形过渡到非轴对称图形。最后出示一个圆和一个平行四边形组成的非轴对称图形。

层次三：多个基本图形组成的组合图形的对称与等分。材料中先提供了五个圆组成的轴对称图形，然后变化圆的位置，过渡到非轴对称图形（如图2）。

与第一、二层次的材料相比，第三层次的材料更具挑战性，也更具吸引力。教师没有继续安排三个图形的组合，而是安排了五个图形的组合。为了使学生“跳一跳能摘到果子”，材料仍然先出现轴对称组合图形，再到非轴对称组合图形。这样处理既不高于学生的思维水平，让学生感觉无从下手，也没有让学生的认知停留在低水平上，束缚学生思维的发展。特别是非軸对称组合图形，给学生留有一个自由的、广阔的空间，使学生打破原有的思维方式和习惯，从多角度、多层次来思考问题，拓展了学生思维的广度与深度。

整节课学习材料的安排遵循从具体到抽象、从简单到复杂、从低级到高级的儿童认知发展规律。学习材料之间存在一定的内在层次性和关联性，有助于促进学生对数学知识和数学规律的理解。学生在学习过程中始终有“柳暗花明又一村”的新鲜感，不但学习兴趣浓厚，而且思路得到拓宽，思维定势被打破，实现了从现有发展水平到潜在发展水平的提升。同时，学生不仅实现了思维拔节，还掌握了学习数学的方法。由此可见，学习材料的开发和利用已经成为发展学生思维的先决条件。在需要提供学习材料的课型上，教师选择材料时应关注这样几点：（1）把握学生的原有认知水平，只有贴近学生的学习起点，才能激发学生的学习兴趣。（2）选择有思维含量的学习材料，一节缺乏智力挑战的数学课，即使课堂气氛再活跃，也算不上一节好课。只有准确定位学习材料的思维含量，才能激发学生的探究欲望。（3）提供适量的学习材料，不能太多也不能太少，过多会分散学生对关键知识点的注意，过少则缺少探究价值。

二、巧妙设计参考性的教学问题——搭建思维拔节的支架

问题是数学的心脏，也是数学思维发展的起点。数学思维的过程就是不断提出问题和解决问题的过程。一般来说，课堂问题可分为是非性问题、展示性问题和参考性问题，它们的性质各不相同。三类问题对于学生的思维要求逐步提升，而课堂上学生的思维往往就在提出参考性问题之后得到拔节。好的参考性问题是学生从数学活动奔向教学目标之间的思维阶梯，是思维拔节的脚手架。因此，教学中我们要深层地思考问题的性质，精心设计问题，为学生搭建导向性支架，引导学生按正确的、有价值的方向拔节。本节课在问题设计上提供了三次支架。

支架一：引导学生从图形的对称性想到非对称性；支架二：引导学生从找出将轴对称图形分成面积相等的两部分的直线，到找出将非轴对称图形分成面积相等的两部分的直线；支架三：引导学生从经过一个中心点把图形分成面积相等的两部分，到经过两个中心点把组合图形分成面积相等的两部分。

当然问题源自学习材料，一个好的学习材料再配以深度的问题，学生的潜在能力将得以发掘。整节课中，参考性问题为学生奔向教学目标提供了必要的指引。在问题的引领下，学生开展了有结构、有序的活动。在学生的思维陷入困境时，教师的问题可谓一盏明灯，为更深入地开展数学思维活动提供方向和动力，适时地引领学生实现思维拔节。

三、合理组织主体性的探究活动——催生思维拔节的力量

在当下的课堂中，学生的思维常常被教师束缚，跟着教师跑，没有时间进行主动思维，思路被牢牢地捆绑在教师的讲授上。在此过程中，学生体会不到成功的快乐，长此以往，对教师提出的问题也就不愿意思考了。因此，要让学生有足够的时间和空间经历观察、实验、猜测、验证、推理与交流等数学活动过程。学生只有通过亲身验证，卷入到学习过程中去，才能产生由内而外的学习动力。本节课中层次清晰的数学活动，为学生思维拔节提供了条件。

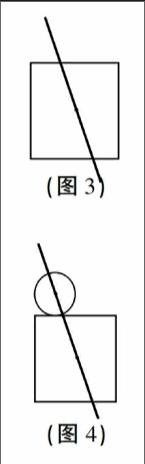
层次一：在研究单个基本图形时，学生提出猜想：经过正方形的中心点画出的直线可以将它分成面积相等的两部分（如图3）。

层次二：在研究一个圆和一个正方形组成的非轴对称图形活动时，学生要验证经过圆和正方形的中心点画出的直线能否将组合图形分成面积相等的两部分（如图4）。

层次三：在找出一条直线把五个圆组成的组合图形分成面积相等的两部分的活动中，学生把它想象成两个基本图形后再画直线。

儿童的思维是从动作开始的，切断动作与思维的联系，思维就不能得到发展（皮亚杰语）。综观上述一系列的实践操作，使学生在不知不觉中经历了“猜想—验证—归纳—应用”的过程，有助于积累学生的思维活动经验。同时，课堂中通过富有挑战性的活动，有效激发了学生的主动思考，使学生深度参与认知活动，增强了思辨能力，实现了学力提升。

面对充满无限可能的学生，教师要努力在数学课堂上深入挖掘学科自身的价值，将这种价值转化为教学行为，最大限度地唤起学生学习的理解力、建构力、思辨力、想象力与创造力。只有把握学科价值和学力生长之间的联系，找到最佳的生长点，按照学生的思维特点推进教学，才能将学生的学力发掘出来、激励出来、开发出来。