考题回归找寻规律

☉江苏盐城市明达中学 朱学慧

考题回归找寻规律

☉江苏盐城市明达中学 朱学慧

纵观江苏十三大市近几年的中考题，有许多可圈可点的地方，而江苏南京2014年的最后一题却给我留下了深刻的印记，细细品味，仍然回味无穷.当然，一道如此精彩的好题追根究底，必然能“回归”为某一知识点，由复杂回归简单，由陌生回归熟悉，从而体现所蕴含的思想.本文就以此题为例与读者交流其中的“回归”.

一、原题呈现

【提出】

学习了三角形全等的判定方法和直角三角形全等的判定方法后，可以继续对“两个三角形满足两边和其中一条边的对角分别相等”的情形进行研究.

【思考】

在△ABC和△DEF中，AC=DF，CB=FE，∠B=∠E.随后，可以对∠B进行分类，分为“直角、钝角、锐角”三种情况进行探究.

【探究】

情况1：当∠B为直角时，△ABC≌△DEF.

（1）如图1，在△ABC和△DEF中，AC=DF，CB=FE，∠B=∠E=90°，根据_____，可知Rt△ABC≌Rt△DEF.

图1

情况2：当∠B是钝角时，△ABC≌△DEF.

（2）如图2，在△ABC和△DEF中，AC=DF，CB=FE，∠B=∠E，且∠B、∠E都是钝角.求证：△ABC≌△DEF.

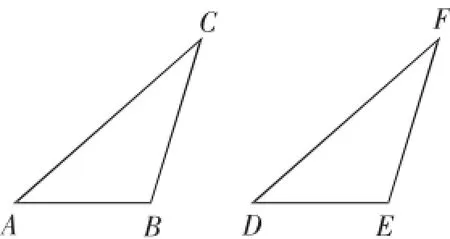
图2

情况3：当∠B是锐角时，△ABC和△DEF不一定全等.

（3）在△ABC和△DEF中，AC=DF，CB=FE，∠B=∠E，且∠B、∠E都是锐角.请你用直尺与圆规在图3中作出△DEF，使△DEF和△ABC不全等.（不写作法，保留作图痕迹）

图3

（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接填写结论：

在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若_______，则△ABC≌△DEF.

分析：本题是学生在八年级学习第一章时，探索三角形全等的条件过程中遇到的疑惑的再研究，即“边边角”能否证明两个三角形全等，是弥补课堂上师生“意犹未尽”的遗憾的体现.此题从考查形式上看，填空、证明、作图、探究均有，可谓让不同的学生都能有得分的机会；从考查内容上看，考查三角形全等的相关知识，是对数学活动经验的一种检验；从考查意义上看，要求教师在课堂上留给学生足够的空间和时间研究问题，符合新课程的理念.本题第（1）问是最特殊的情形，从直角三角形引入，让每一个学生都能入手；第（2）问是常规全等的证明，分别过点C、F作边AB、DE的高，将钝角三角形转化成直角三角形，便可通过两次全等证明将问题解决；第（3）问画锐角三角形的反例图，以合情推理为要求，有一定的思维价值；第（4）问以分析问题、解决问题为核心，综合考查学生的思维能力及应用意识，给人耳目一新的感觉.本题解法多样、层次分明，研究价值高，探索味道浓，有较好的区分度和推广价值，而且答案开放性高，兼顾不同层次的学生，是一道不可多得的好题.

二、题目“回归”

可以说，这道压轴题的产生并非偶然，学生在课堂上曾经探索过三角形全等的条件，但教师在讲解“两边一角”证明三角形全等时，往往只注重对“SAS”的讲解，常忽视对“SSA”的深入研究，故学生只片面知道“SSA”不能证明全等，却不了解在某些条件下“SSA”也能成立，上述压轴题的产生就是课堂上需要深入探究但恰恰未探究的地方，即课堂上意犹未尽的问题.

笔者曾以“SSA”为载体，在中考一轮复习的时候，让学生研究过下述问题，此题与2014年南京中考压轴题有异曲同工之处：已知∠BAC=45°，AB=4，要使△ABC唯一确定，那么BC的长度需满足的条件是_______.

观察题目后易发现，点A、B的位置是相对固定的，而点C的位置不确定，此题又要求在△ABC唯一确定时求BC的长度，故仔细分析后可转化为另外两种问法：

问法1：以点B为圆心，BC长为半径作⊙B，当⊙B与射线AC有唯一公共点C时（点C与点A不重合），求BC的长度.

问法2：在射线AC上存在一动点C（点C与点A不重合），连接BC，使得BC为某一长度时不会存在两个不全等的△ABC，求BC的长度.

图4

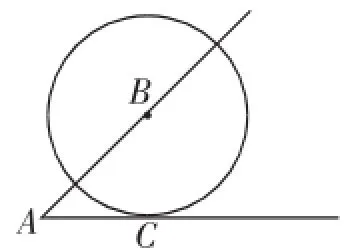
图5

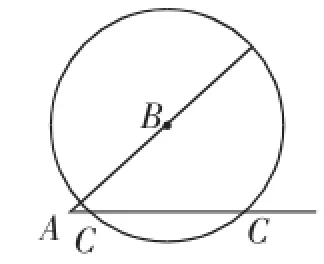
图6

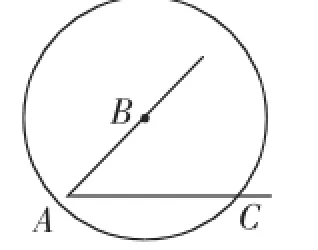
图7

评析：本题虽然为填空题，但读懂题目却并非易事，题目有一定难度，学生不能理解“唯一确定”这四个字的正确含义，若能攻克此问题，题目便能迎刃而解.事实上，该题可以理解成圆与射线只有一个交点的问题（如图4～图7），圆与射线只有一个交点便为图5的相切或图7的情形，图6有2个交点，意味着△ABC不能唯一确定，即满足“SSA”的两个三角形不一定全等，但随着角度的变化，答案也会随之发生改变.

三、推广研究

事实上，“回归”题中的条件就是三角形的两边及一对角，通过研究学生已经可以感受到“SSA”有可能存在成立的情形，如果能将题目再深入往下研究，就形成了2014年的中考题，便可将三角形全等的条件彻底掌握，从而题目也趋于完整.课堂上还可以研究这样的问题：在△ABC中，∠ABC=30°，AB边长为4，AC边的长度可以在1、2、3、4、5中取值，满足这些条件的互不全等的三角形的个数是_______.

题目还可以进一步推广：

推广1：两边及其中一边的对角分别相等的两个锐角三角形一定全等吗？如果成立，请给出证明；若不成立，请说明理由.

推广2：两边及其中一边的对角对应相等的两个钝角三角形一定全等吗？如果成立，请给出证明；若不成立，请说明理由.

推广3：两个四边形全等需要几个条件？试举例说明.

四、总结反思

中考，有反思教学和甄别人才的功能.现行教学过程中，存在着重技巧轻通性通法、重知识轻能力、重结果轻过程的现象.这些不良的教学现象严重遏制了学生能力的发展，让学生缺乏自主探究的意识，所以教师要在教学前自己先多深入研究，寻找适合学生学习的资源，教学后再多反思，与学生共同挖掘题目背后的规律和本质，让学生知道，如何去思考和解决此类数学问题，这样才能真正帮助学生，走一条行之有效的教学道路.所以笔者提倡在中考复习前，一定要善用中考题，因为中考题是专家们的心血之作，也代表了一个地区命题的风格，多对中考题及变式进行训练，对学生短期的提升很有帮助.

1.回归课本，探寻本质.

细细研究近几年的中考题，不难发现，许多题目源于课堂、源于课本、源于生活.故笔者建议教师在教学的过程中要重视课本的教学，以课本为载体，给学生足够的时间和空间去弄懂概念，剖析概念的本质，弄清概念的外延和内涵，同时在学习的过程中，让学生体会研究数学问题的步骤、思路和方法.中考前的复习，可以选择合适的中考题作为上课的重点，贯彻一道题就是一节课的理念，深入研究，真正研究透彻.

2.类比研究，探寻规律.

波利亚对于解题有着自己独到的见解，他曾说过：“类比是一个伟大的引路人.”上述例子，从中考题到回归题，再到推广问题，强化了学生对某知识的掌握情况，题组层层相扣，由易到难，让学生对此类问题研究得更深刻、理解得更全面，达到启发思维，做一题、会一类、通一片的效果，实现学习经验的迁移，让学生的思维能力有所提升，从而实现高效课堂，学生在中考中也能胜人一筹.