发现关联递进解题
☉江苏东台市实验中学教育集团 崔恒刘
发现关联递进解题
☉江苏东台市实验中学教育集团 崔恒刘
牛顿从苹果砸头的情景中发现万有引力,瓦特从开水壶嘴喷气的情景中发明蒸汽机……任何发现、发明离不开必要的情景,因此新课程标准提倡探究性学习,要求在新知识的学习过程中,先创设必要的情景,再引导学生观察、猜想,不断尝试,以期从中发现规律并应用规律解决问题.体现在近几年的中考压轴题中,出现了“分析试题提供的信息和内部的结构特点,发现并利用其隐含的关联效应解题”的新趋势.本文以2016年淮安市中考试题第28题为例说明这类考题的应对策略.
一、中考真题
问题背景:
如图1,在四边形ADBC中,∠ACB=∠ADB=90°,AD= BD,探究线段AC、BC、CD之间的数量关系.

图1
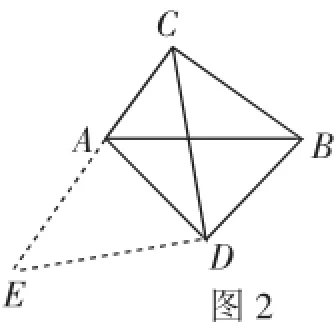
图2
小吴同学探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图2),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以从而得出结论:AC+ B
简单应用:
(2)如图3,AB是⊙O的直径,点C、D在⊙O上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
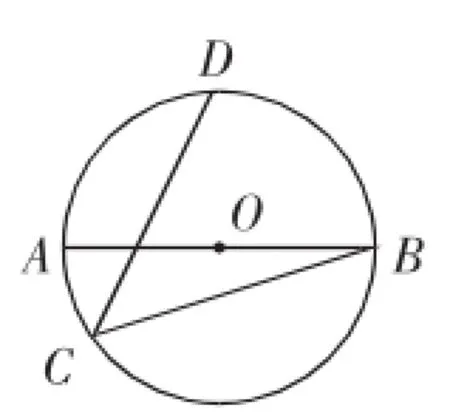
图3
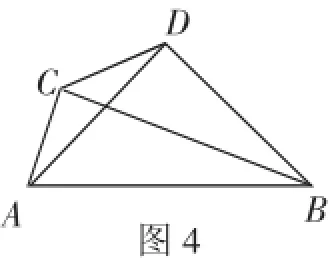
图4
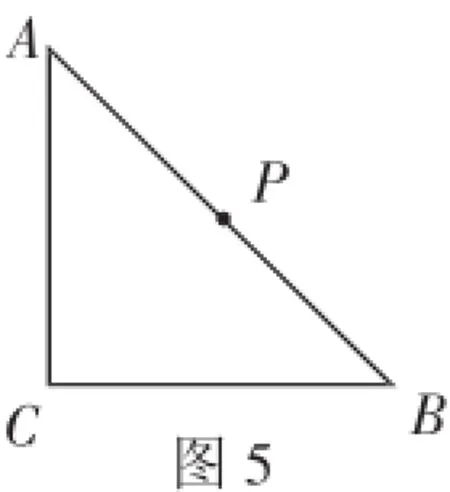
图5
拓展规律:
(3)如图4,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m、n的代数式表示).
(4)如图5,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=C,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是________.
二、思路探究
首先要读懂问题背景提供的模型:四边形由有公共斜边的两个直角三角形组成(公共斜边的两侧),其中一个是等腰直角三角形,则另一个直角三角形的两直角边之和等于四边形两个直角顶点之间距离的
第(1)问是热身,它把背景问题数量化,只要将给出的AC与BC的长度值代入问题背景提供的结论AC+BC=,即可得出CD的长度,属于送分题.
解答(2),勿忘(1),第(2)问改变了问题的情景,将直线型的图形放置在圆中,由于已知AB为⊙O的直径,且弧AD=弧BD,则必然会想到圆的相关性质:直径所对圆周角为直角,同圆中等弧所对弦相等,由此提示我们连接AC、BD、AD,便有了问题背景提供的模型“有公共斜边的两个直角三角形组成(公共斜边的两侧)的四边形,其中一个是等腰直角三角形”,利用问题背景所给出的证明思路即可求出CD的长度;牢记问题背景提供的模型真的好解题.
第(3)问与问题背景不同的是:由在斜边两侧的两个直角三角形变为了在同侧的两个直角三角形,怎么办?转化,构造背景提供的模型,然后利用问题背景提供的模型求解.第(2)问中多了个圆,试试作以AB为直径的⊙O,如图6,圆是轴对称图形,因此把△ABD沿直线AB翻折,又有了问题背景提供的模型,由此可求CD1,D1D是直径,所以利用勾股定理即可求出CD的长度.
第(4)问,题图简单,问题是图没画全,要我们自己画图,肯定有文章,原来点E的位置有两种,一是点E在直线AC的右侧,二是点E在直线AC的左侧.分别画出图7、8,下面的事就是尝试构造问题背景中的模型.等腰、中点,连接CQ、CP后,问题背景中的模型便有了.
三、试题解答
(1)由问题背景提供的信息,可知:AC+BC=■:2CD.
将AC与BC的长度值代入:

(2)连接AC、BD、AD.
在⊙O中,由AB是⊙O的直径,得∠ADB=∠ACB= 90°.又AB=13,BC=12,则AC=5.
由弧AD=弧BD,得AD=BD.
由于∠ACB=∠ADB=90°,所以OA=OB=OC=OD,所以A、C、D、B四点都在⊙O上.连接DO并延长交⊙O于点D1,连接D1A、D1B、D1C,则∠AD1B=90°.由AD=BD,得AD1= BD1,如图6.
由D1D是⊙O的直径,得∠DCD1=90°.
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=m2+n2.
在Rt△DCD1中,由勾股定理,得DD12=CD12+CD2.

图6

图7
(4)当点E在直线AC的左侧时,如图7,连接CQ、PC.
由AC=BC,∠ACB=90°,点P是AB的中点,得AP=CP,∠APC=90°.
由CA=CE,点Q是AE的中点,得∠CQA=90°.
当点E在直线AC的右侧时,如图8,连接CQ、CP.
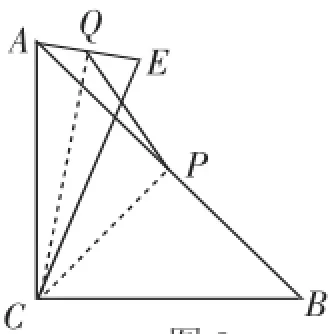
图8
同理可知:∠AQC=∠APC=90°.
设AC=a.
四、教学反思
布鲁纳说:“学习不但应该把我们带往某处,而且还应该让我们日后的继续前进更容易.”波利亚指出的:“在解题的每一阶段……我们都要用已经得到的知识去得出更多知识.我们要靠逐省逐省的占领去最后征服一个王国.在每个阶段,我们利用已被征服的省份作为行动基地去征服下一个省份.”本题提供问题背景,让学生在阅读理解的过程中,掌握一个基本模型,再在简单应用环节中,用问题(1)让学生直接套用基本模型以进一步熟悉模型,设计问题(2)让学生应用所学知识构建基本模型解决问题,以加深理解基本模型;问题(2)比问题(1)进了一步;在拓展规律环节中,对基本模型进行变化,将两个直角三角形在公共斜边的两侧变为同侧设计问题(3),引导学生深入研究问题,要想顺利解答问题(3),必须回到基本模型中,深入理解基本模型的研究思路,寻找变化后的问题与基本模型之间的关系,有效地化归问题;问题(4)则体现了基本模型的应用价值,题中画图留白,提醒学生注意分类研究.四个问题,每一问都紧扣着前一问,运用规律、层层递进、创新探究,体验数学的建模思想和应用价值,对学生的创新思维进行考查,有利于开展研究性学习,实现数学的人文教育功能.
递进式的综合探究题,编制上往往有一个特点,就是问题设计层层深入,后一个问题的解答或者直接应用上一个问题的结论,或者类比上一个问题的研究思路方法.表现在能力层次上的要求为:模仿→构建→运用.解题的应对策略是:首先,要理解题目提供的问题背景,即基本模型,只有在理解了基本模型的基础上才能运用基本模型;其次,探寻问题与基本模型之间的关系,将要解决的问题转化为基本问题.化归思想在数学中几乎无处不在,它是数学教学中最基本的思想方法,在递进式的综合探究题中显得特别抢眼.
数学解题是一个不断地将未知转化为已知,由不熟悉转化为熟悉的过程,命题者在命题时会铺设台阶,一步一步提升难度.在解题时,我们要将题中的条件与问题联系起来观察、比较、联想,从而发现题目内部的关联、递进关系,洞察命题者发出的暗语:层层诱导,先通过特殊情形认识问题,再进一步解决特殊化的数学问题,最后利用上述形成的结论或方法,来解决后面的数学问题,最终顺利解决问题.近年来,中考数学压轴题特别重视突出数学思想和方法的考查.因此,在平时的教学中,要注意体会、归纳教材、题目中的数学思想方法.尤其在中考复习时,教师更应有意识、有目的、适时地渗透数学思想方法,从解题过程中获取解题经验,感受解题过程中的思维体验,培养学生有效利用数学思想方法解决相关问题的能力.
1.波利亚:数学的发现[M],呼和浩特:内蒙古人民出版社,1982.

