数学实验:赋予儿童几何学习以生长的力量
【摘要】“图形与几何”是小学数学教学中重要的领域,它承载着极其丰富的数学实验内容。科学有效的数学实验不仅能帮助学生理解几何形体的特征,体验几何原理的生长过程,也是学生建立和发展空间观念、提升数学学力、培育数学情感的重要途径。
【关键词】“图形与几何”;数学实验;几何学习;空间观念;范式建构
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2017)09-0031-03
【作者简介】毛新薇,江苏省江阴市徐霞客实验小学(江苏江阴,214406)副校长,高级教师,无锡市数学学科带头人。
在“图形与几何”内容领域开展数学实验是指学生在学习几何知识时,能够借助一定的工具,开展平移、折叠、拼合等积极的实践活动,在“数学化”的过程中理解知识、积累经验、发展空间观念与空间想象力。在教学“图形与几何”领域的内容时开展科学有效的数学实验,不仅能帮助学生正确理解几何形体的特征,体验几何原理的生长过程,也有助于学生建立和发展空间观念、提升数学学力、培育数学情感。
一、寻绎:教材文本中的实验基因
在蘇教版小学数学教材中,“图形与几何”领域包括图形的认识、测量、运动与位置这四大内容。依据实验的目的,笔者将这四大内容中的数学实验分为理解型、探究型和验证型三类。理解型实验有:圆锥的认识;做圆柱与圆锥,求底面周长与底面积;量圆锥实物,理解高与底面;理解平面图绘制中各部分的占地形状;等等。探究型实验有:圆柱的认识;选择合适规格的铁皮做长方体;等等。验证型实验有:摆正方体,从不同方向观察其形状;折正方体并展开,验证其展开图;等等。
二、建构:“图形与几何”领域中数学实验的操作范式
笔者重点提炼了“图形的认识”“图形的测量”“图形的运动”这三个范畴中数学实验的范式。在具体实施时,教师应根据具体情况灵活调整,形成适合教学实际的“变式”,以更好地提高实验教学的有效性。
1.“图形的认识”的实验范式。
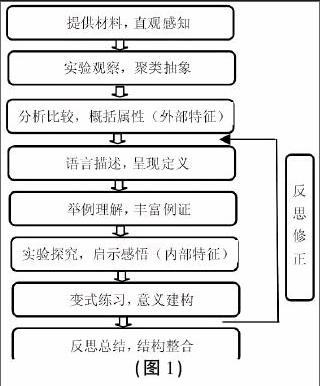
“图形的认识”是空间形式的本质属性在人脑中的反映,它是“图形与几何”领域的重要内容,其大部分内容均与概念教学有关,属于“形概念”教学。“图形的认识”的实验范式如图1所示:
2.“图形的测量”的实验范式。
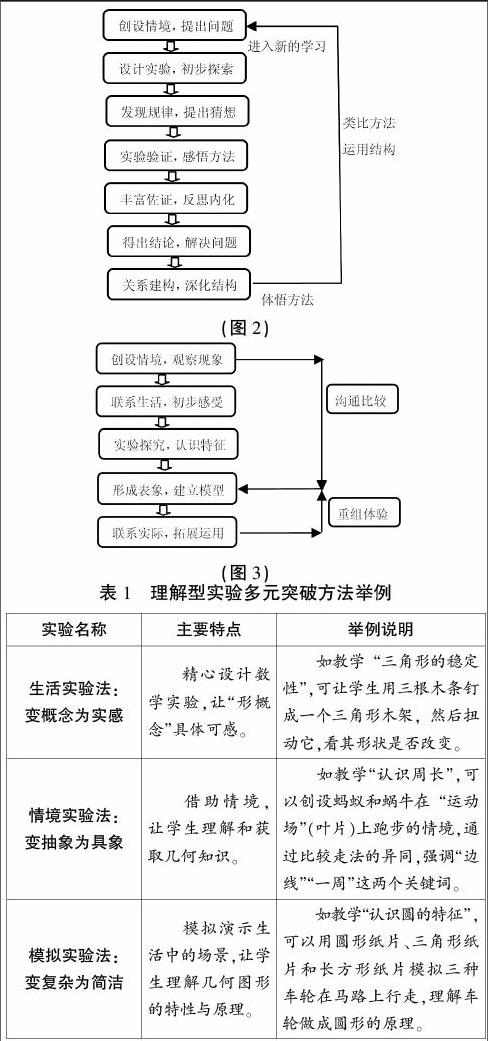
“图形的测量”是学生三维空间观念逐步建构和完善的过程,主要包括长度、面积、体积的度量和图形周长、面积、体积的计算公式推导两大部分。笔者以计算公式的推导为例,说明“图形的测量”的实验范式(如图2)。
3.“图形的运动”的实验范式。
“图形的运动”领域的学习可以帮助学生从平移、旋转、轴对称变换等运动变化的角度认识图形,了解图形之间的联系以及数学与现实世界的联系,感受、欣赏图形的美,激发学生的创造潜能,其实施范式如图3所示:
三、深耕:“图形与几何”领域实验教学的智性实践
1.理解型实验:“高观点”下洞悉“图形与几何”知识的数学本质。
理解型实验是为了让学生形成“形概念”,理解图形的特征,体验图形的多方面性质(如度量性质、组合性质、稳定性质等),体悟定理、公式产生的原理而进行的实验。教师应站在“制高点”上审视理解型实验的价值,根据学生对几何知识的认知规律设计实验,让学生真正洞悉几何知识的本质属性。
(1)多元突破:丰盈学生的感知力
根据学生认知结构的特点,教师可以采取多种途径与方法来帮助学生感知几何知识。表1中列举了几种实验方法。
(2)举象会意:丰满学生的表象力
教师要通过数学实验给予学生丰富的表象,让学生通过表象来领会几何知识的意义,从而使他们更好地进行抽象的“思”。例如:苏教版三上《轴对称图形》的实验教学,一是从生活实例中抽象出轴对称图形,让学生通过观察直观建立“前表象”概念;二是通过折一折、比一比等操作活动概括轴对称图形的本质属性,寻求其背后的物质表象,建立“准表象”概念;三是借助长方形、正方形纸片等工具,设计、创造一个轴对称图形,以此丰富学生的元认知表象,实现内化与跃迁。
(3)逐层推进:丰厚学生的理解力
教师在设计数学实验时,要按照知识的逻辑程序和学生的认知程序进行梯度式实验,分层推进,逐步建构。例如:教学苏教版五下《圆的认识》,教师先呈现圆形的实物图形,让学生感受圆的基本特征,这对应学生对感官型概念理解的心理水平;其次,让学生用圆规或自主设计画圆工具来画圆,概括圆的本质属性,这对应学生对工具型概念理解的心理水平;最后,让学生用圆形图片模拟车轮沿桌面边缘滚动,猜想车轴的运动轨迹并解释将车轴装在圆心的原理,这对应学生对关系型概念理解的心理水平。三层实验和三度思考,有助于学生深入地理解圆的概念。
2.探究型实验:让学生深入进行几何学习。
探究型实验是指学生事先不知道结论,通过开展有针对性的探究实验活动获取结果。在教学几何图形的定理、公式时,教师可以借助数学实验,让学生深入进行探究活动,亲历数学知识的形成过程,体验探究成功的乐趣。
(1)“姿态”大气:从控权到放权
教师要做到“姿态大气”:在理念上,要从只关注知识技能培养走向关注人的发展;在方式上,要从离身学习走向具身学习;在材料上,要从封闭单一走向开放多元;在过程上,要从小步子推进走向大空间探究。当然,“放权”不是放任自流,当学生实验受阻或偏离方向时、实验方法不科学或数据失真时、探究结论遇到困难时,都需要教师的指点、帮助和引领。
(2)过程完整:从操作到内化
郑毓信教授曾指出:“数学实验要实现对操作层面的必要超越。”数学实验活动的外化与数学思维品质的内化是相互统一的,数学实验不能停留于实验操作的层面,而应引导学生在头脑中实现必要的重构,在活动过程中理解几何对象的内在属性,提升几何思维水平。
(3)视野完好:从现象到本质
在实验时,学生往往只会关注那些表面的、外在的、直观的现象,而很难深入知识的深层内核,挖掘知识的本质,这就需要教师加以引导,帮助学生体悟现象背后的本质属性。例如:苏教版五上《平行四边形的面积》实验教学结束时,教师可以引导学生发现实验背后的本质,感受平行四边形可转化为长方形,从而对图形的特征及其内在关系建立起基本的数学感觉。
3.验证型实验:开掘学生几何学习的潜能。
验证型实验是指学生已经知道或者大概知道结论,通过实验操作和观察、记录、分析等手段,尝试运用所学知识和方法對已有的数学猜想给出证明或“再发现”“再创造”的实验。这类实验对学生推理能力、实践能力和理性精神的培养有着不可替代的作用。
(1)猜想:验证的起点
教师要引导学生经过推导大胆地提出自己的合理猜想,同时要追问学生猜想的依据是什么,帮助学生调整思路、筛选结果,不断提高学生的猜想水平。如教学苏教版六下《长方体的体积》练习课时,有这样一道题目:把一张长5cm、宽4cm的长方形纸分别绕它的长和宽旋转一周,形成的物体是什么形状?它的体积最大是多少?教师可以引导学生进行深度猜想:一是利用已有生活经验来猜想;二是融入动态表象,让学生进行动态操作想象,使长方形在他们头脑中“动”起来,建立起一个连续、渐变的圆柱表象。
(2)实验:验证的基点
教师通过设计多维互证的方式,让学生采用多种方法来进行实验。例如:教学苏教版六下《圆锥的体积》时,在学生猜测后,教师可以提供多种实验材料,让学生分组验证。面对富有挑战性的实验材料,学生可能会想出多种验证方案:用橡皮泥捏等底等高的圆柱与圆锥寻求体积关系;削圆锥形萝卜后称重量比较;通过注水法探求体积关系;等等。然后引导学生在动手操作的过程中印证圆锥体积公式的合理性。
(3)有本有源地思辨:验证的落脚点
为了使学生避开操作误差的干扰,教师可以带领学生进行思想实验,引导学生通过进行理性的思辨寻求结论背后的理论支撑,以增强结论的可信度。例如:教学《圆锥的体积》一课,在学生通过动手操作获得结论后,教师可以以“你知道吗”的形式补充圆锥体积的推导过程:用平行于圆锥底面的平面把它切成一些近似的小圆柱,将这些小圆柱的体积求和就近似于原来圆锥的体积,切成小圆柱的份数越多,结果就越精确。这样的理性推导,直抵圆锥公式的本源,既与操作的结论相印证,又能拓展学生的知识视界,培养学生的分析、推理能力,让学生的验证真正落到知识本源处。
总之,从本质上看,学习是一种基于经验的自然生长。生长需要土壤、水分和阳光,而数学实验因其独特的内在价值,能够成为学生空间观念培养与数学素养提升的加速器,能够赋予学生的几何学习以生长的力量。<\\Ysc02\d\邱\江苏教育\小学版\2017\02\KT1.TIF>
【参考文献】
[1]张景中,王鹏远.少年数学实验[M].北京:中国少年儿童出版社,2012.
[2]董林伟.初中数学实验教学的理论与实践[M].南京:江苏科学技术出版社,2013.
注:本文获2016年江苏省“教海探航”征文竞赛一等奖,有删改。

