异步电机的磁链观测和转速辨识研究

贺虎成，行俊锋，张玉峰，祁玄玄

(1.西安科技大学，西安 710054；2.合肥工业大学，宣城 242000)

异步电机的磁链观测和转速辨识研究

贺虎成1，行俊锋1，张玉峰1，祁玄玄2

(1.西安科技大学，西安 710054；2.合肥工业大学，宣城 242000)

准确的辨识电机转速，可进一步提高异步电机无速度传感器矢量控制系统的性能。通过分析电压模型和电流模型获得了磁链的混合观测模型，利用该模型估算出转子磁链和磁场定向角，并进一步辨识电机转速。搭建了以TMS320F28335为控制核心的硬件平台，对磁链观测和转速辨识进行了实验验证，表明该辨识算法可行。

异步电机；转子磁链观测模型；转速辨识；无速度传感器；矢量控制

0 引 言

目前，电机速度反馈量普遍采用传感器进行测量。因此，必须在电机轴上安装位置传感元件或者光电数字脉冲编码器等仪器。但这会带来许多问题，比如系统维护困难、鲁棒性降低、不适用于恶劣场所等等。因此近些年来无速度传感器的高性能异步电机交流调速系统越来越受到人们的普遍关注。

磁链观测和转速辨识直接决定无速度传感器矢量控制系统的性能。常见的磁链观测模型有电压模型和电流模型。电流模型易受电机参数和转速的影响，在高速时估算不准；而电压模型涉及纯积分环节，所以存在累计误差和漂移问题，在低速时估算不准。转速辨识的控制方式主要有定子电流转矩分量误差补偿法、感应电动势计算法、模型参考自适应MRAS法和转子磁链角速度计算法[1-3]。本文采用电压模型和电流模型混合的转子磁链观测模型，选取合适的PI参数，充分发挥了电压模型和电流模型的优点，利用转子磁链观测模型的输出，作为速度辨识的输入，辨识电机转速，并在转速辨识实验平台进行了验证。

1 转子磁链观测模型分析

转子磁链观测模型是实现转矩和励磁解耦的重要模型, 它所计算出的磁场定向角和转子磁链是实现解耦和转速辨识的重要参数。通过电压模型和电流模型可推导出混合磁链观测模型，这样就可以使磁链观测模型根据不同的转速应用不同的模型，在全速范围内都有一个较准确的估算值[4]。转子磁链的电流模型方程如下:

电流模型法:

(1)

(2)

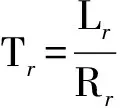
在两相静止坐标系中，由电流模型中转子磁链方程可得定子磁链的方程：

(3)

(4)

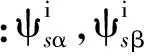
(5)

(6)

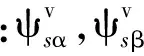
(7)

(8)

式中：Kp为比例增益，Ki为积分增益。根据式(5)、式(6)得到的定子磁链，再通过对式(3)、式(4)进行整理，可得基于电压模型下的转子磁链方程式：

(9)

(10)

由此，便可以求得转子磁链幅值和磁场定向角的计算公式分别：

(11)

(12)

根据以上算法可得转子磁链估算模型框图如图1所示。

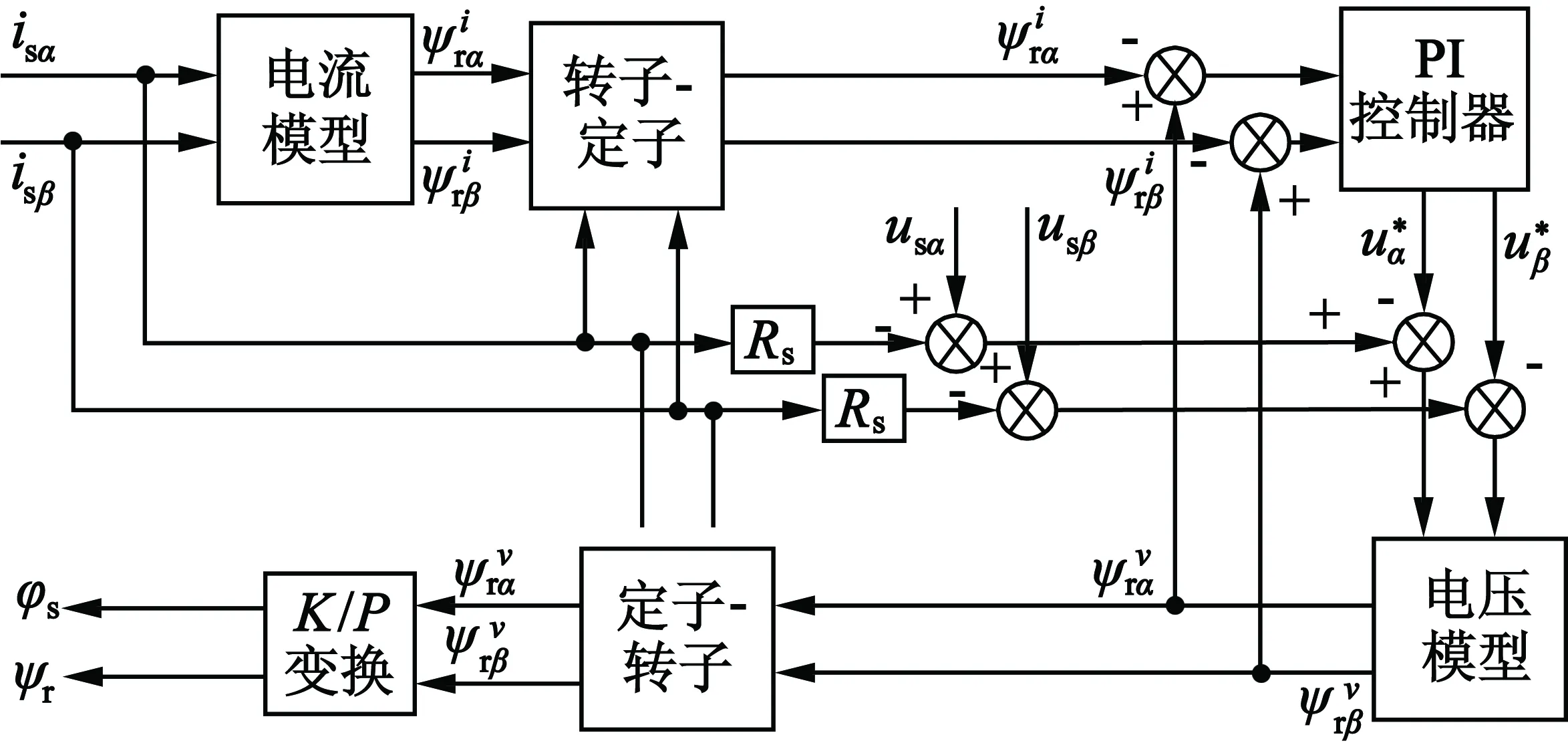
图1 磁链估算系统框图

2 转速辨识方法

无速度传感器就是去掉电机上原本装有的速度传感器，不经过传感器反馈转子转速，而是通过间接法获得电机运行的实际转速[5]。无速度传感器应用的前提是必须要能准确地辨识转子实际转速，本文采用的速度估算方法是基于反电动势的速度估算法，即利用基于反电动势的转子磁链估算模型中算出的磁场定向角 ，进一步算出同步角速度 ，然后减去转差角速度 ，最终得到转子实际角速度[6]。这种算法结构简单，受电机参数影响较小。

通过对磁场定向角方程式(12)求导，可以得出转子磁链角速度(同步角速度)：

(13)

将式(9)、式(10)整理后带入式(13)有：

(14)

转子角速度ωr能被表示：

(15)

为了防止计算数值较大，对式(15)进行单位化，两边同时除以基本的电角速度ωb=2πfb，fb为基本频率，可得：

(16)

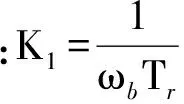
(17)

式(17)中某些数据过高或过低会影响模型的稳定性，而离散化可以减弱极端值的影响，因此，对式(17)离散化，整理得：

(18)

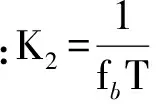
(19)

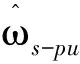
(20)

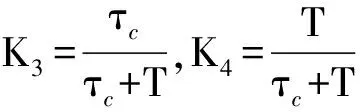
(21)

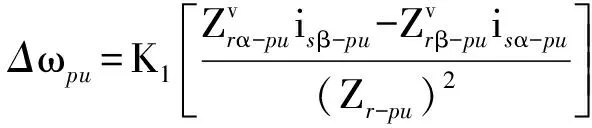
(22)

式中：ωr表示电机的实际角速度。

3 实验研究

3.1 实验装置

无速度传感器矢量控制系统硬件框图如图2所示。主回路采用电压源型交-直-交变频电路，由三相二极管整流和三相桥式逆变两部分组成；控制电路是以TMS320F28335为核心的控制板，主要负责算法实现，母线电压检测电路提供欠压、过压保护等，光耦驱动电路将强电信号和弱电信号隔离开，起到保护电路的作用；电流检测电路将逆变器输出的三相电流经霍尔传感器采集后，调理成适合微处理器采集的电压信号，上位机和面板能实现人机交互和远程通信功能。

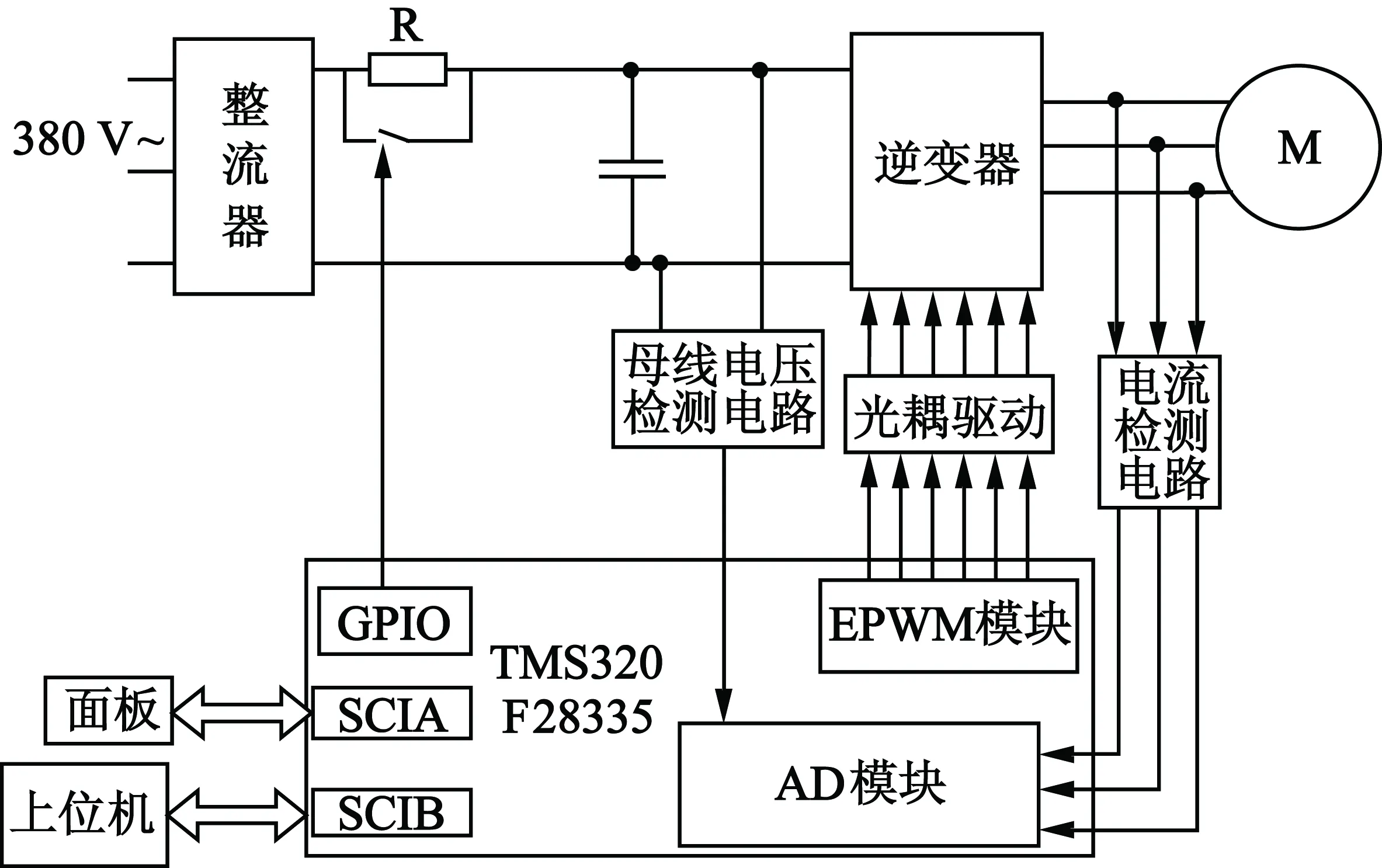
图2 矢量控制系统硬件框图

电机的额定参数为：Pn=11kW，Un=380V，In=24.5A，fn=50Hz，Nn=905r/min，p=6，Rs=0.476Ω，Rr=0.587Ω，Ls=70.98mH，Lr=123.68mH。

3.2 实验结果分析

利用所搭建的矢量变频控制硬件平台，采用上述磁链观测和转速辨识方法进行实验验证。

如图3所示为给定转速为300r/min，在电机运行阶段改变电机转向，从图中可以看出，辨识转速能很好的跟踪实测转速，可准确辨识电机转速。图4为转子磁链波形，从图中可以看出磁链幅值波动较小。图5为磁场定向角的波形。图6为励磁电流和转矩电流波形，在电机运行阶段突加16N·m的负载，带负载运行一段时间后卸掉负载，由图可知，突加负载时转矩电流增大，而励磁电流不变；卸掉负载后，转矩电流立即减小，返回空载时刻的电流值，而励磁电流波形仍然保持恒定，该波形证明，无速度传感器矢量控制系统实现了励磁和转矩的完全解耦。

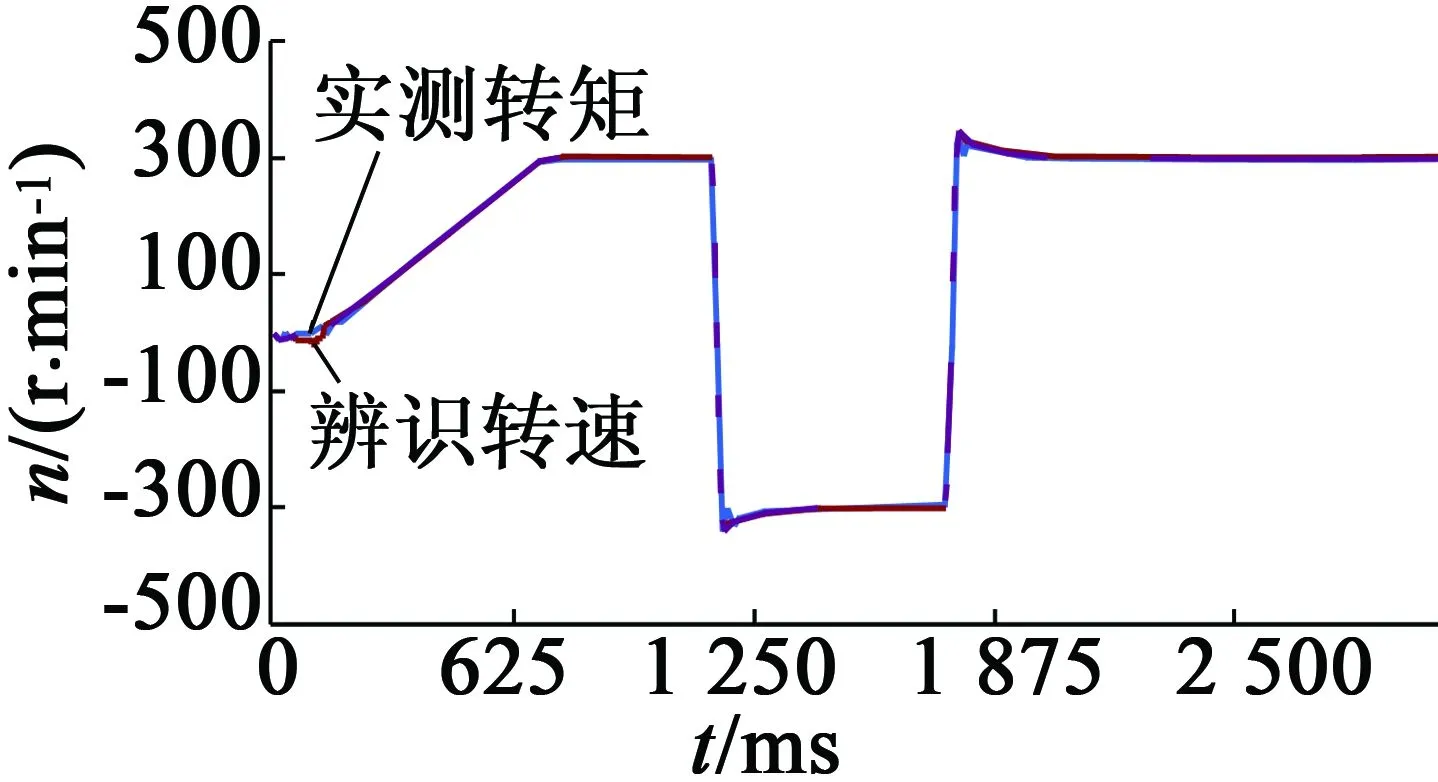
图3 转速波形

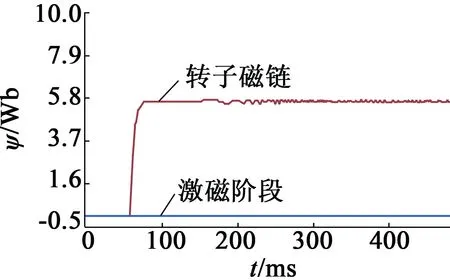
图4 转子磁链波形

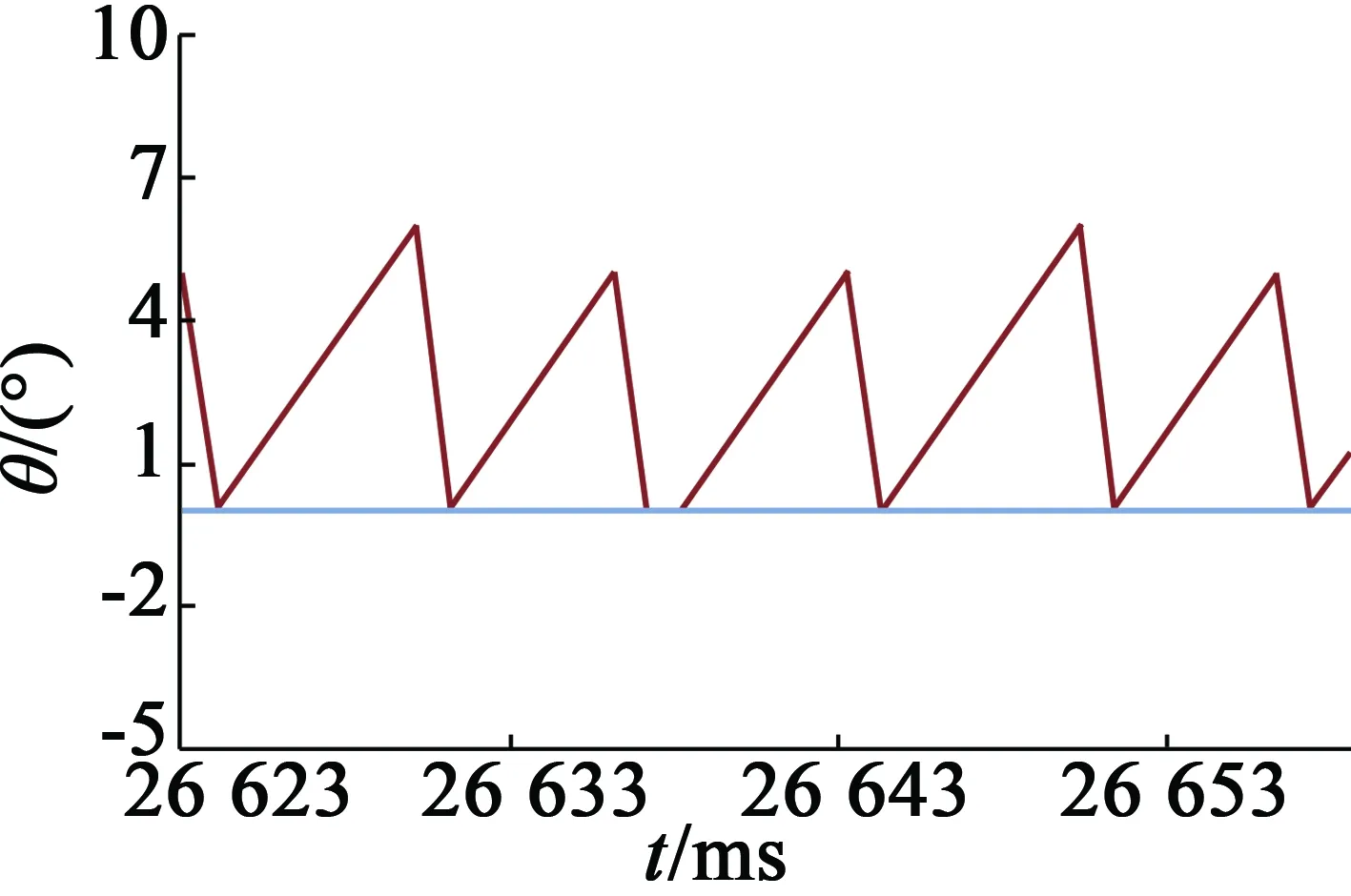
图5 磁场定向角

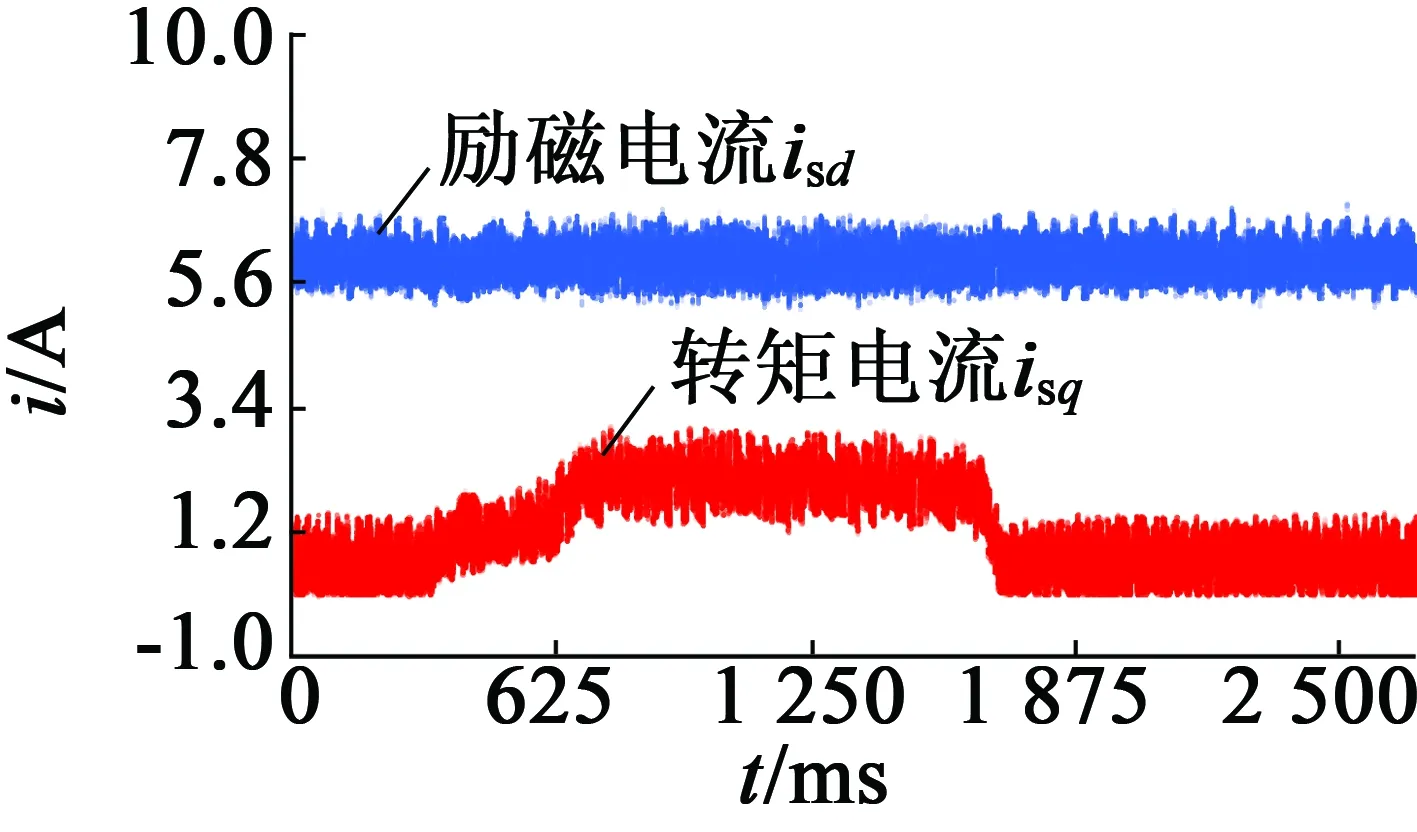
图6 励磁电流和转矩电流波形

4 结 语

本文通过异步电机的磁链电压模型和电流模型，获得了混合磁链观测模型，并利用模型输出准确辨识了电机转速。实验结果表明，该方法具有较好的准确性和实用性，可以应用于无速度传感器矢量控制系统，实现转矩和励磁的完全解耦。

[1] 李华德，白晶，李志民,等.交流调速控制系统[M].北京：电子工业出版社，2003.

[2] 李旭春,张鹏,赵非.改进EKF的异步电机无速度传感器矢量控制[J].电机与控制学报，2013，17(9):24-29.

[3] 李崇坚.交流电机变频调速控制系统的探讨.电力电子,2004(1):20-23.

[4] 杨德刚.三相异步电动机无速度传感器矢量控制系统的研究[D].广州：华南理工大学，2014.

[5] 周亚丽，李永东，郑泽东.基于MRAS的感应电机无速度传感器矢量控制[J].电气传动，2009，39(4):3-8.

[6]TRZYNADLOWSKIAM.Thefieldorientationprincipleincon-trolofinductionmotors[M].Berlin:Spring,2009.

ResearchonFluxObservationandSpeedIdentificationofAsynchronousMotor

HE Hu-cheng1，XING Jun-feng1，ZHANG Yu-feng1，QI Xuan-xuan2

(1.Xi’anUniversityofScienceandTechnology，Xi'an710054，China;2.HefeiUniversityofTechnology,Xuancheng242000,China)

Theperformanceofspeedsensorlessvectorcontrolsystemofasynchronousmotorcanbefurtherimprovedbyaccuratespeedidentificationofmotorspeed.Byanalyzingthevoltagemodelandcurrentmodel,themixedobservationmodeloffluxlinkagewasobtained.Therotorfluxandmagneticfieldorientationangleareestimatedbythemodel,whichfurtheridentifiesmotorspeed.TheexperimentiscarriedouttoverifythefluxobservationandspeedidentificationonthehardwareplatformbasedonTMS320F28335,whichshowsthattheidentificationalgorithmisfeasible.

asynchronousmotor;rotorfluxobservationmodel;speedidentification;speed-sensorless;vectorcontrol

2016-06-27

国家自然科学基金项目(51307137)；陕西省教育厅科研计划项目(15JK1459)

TM

A

1004-7018(2017)01-0070-03

贺虎成(1979-)，男，博士，副教授，研究方向为电力电子技术、智能自动化装置和运动控制技术等。