基于PSO的自适应反推永磁同步电动机DTC控制方法研究

徐艳平，张保程，周 钦，马灵芝

(西安理工大学，西安 710048)

基于PSO的自适应反推永磁同步电动机DTC控制方法研究

徐艳平，张保程，周 钦，马灵芝

(西安理工大学，西安 710048)

针对传统直接转矩控制(DTC)中的磁链转矩脉动大、逆变器开关频率不恒定的缺点，提出了基于微粒群优化(PSO)的自适应反推直接转矩控制方法，该方法中根据永磁同步电动机(PMSM)直接转矩控制原理设计了磁链转矩自适应反推控制器，并针对控制器中参数较多、不易调节的问题，引入微粒群优化算法优化自适应反推控制器中的参数。仿真结果证明了自适应反推控制器参数可通过微粒群优化方法得到，与传统直接转矩控制方法相比，基于PSO的自适应反推直接转矩控制方法可明显减小磁链和转矩脉动，使逆变器具有恒定的开关频率。

永磁同步电动机；自适应反推控制；微粒群优化算法；直接转矩控制

0 引 言

直接转矩控制(DTC)由于系统结构简单、转矩响应迅速等优点，目前已经用于永磁同步电动机(PMSM)中[1-2]。但直接转矩控制方法中磁链和转矩均采用滞环控制，并且只有有限个电压矢量可供选择，使得直接转矩控制具有磁链转矩脉动大、逆变器开关频率不恒定的缺点。由于永磁同步电动机本质上是一个高阶、多变量和强耦合的非线性系统，传统的线性控制方法不能解决输入和输出的独立控制等问题，不能满足高性能调速系统的控制要求。针对上述问题，国内外的学者将非线性理论应用到永磁同步电动机控制系统中。

目前应用到永磁同步电动机中的非线性控制方法主要有反馈线性化方法[3]、逆系统方法[4]、反推控制方法[5]、无源控制方法[6]、自抗扰控制方法[7]、变结构控制方法[8]等。其中，反推控制方法[9-11]适用于可状态线性化或具有严参数反馈的不确定非线性系统，在设计不确定系统(特别是当干扰或不确定不满足匹配条件时)鲁棒控制或自适应控制器方面具有优势。同时在实际电机系统运行时定子电阻和粘滞摩擦系数都会随着定子的温升而改变，并且负载扰动会影响系统的控制精度，因此为改善传统直接转矩控制系统性能，减小电机参数变化对系统性能的影响，本文针对永磁同步电动机，提出了一种自适应反推DTC方法，由于该方法中的自适应反推控制器存在较多参数，不易调节，同时参数的选取对于系统的性能具有关键作用，因此本文引入微粒群优化算法以实现对自适应反推控制器参数的优化，从而使得控制系统具有较小的磁链和转矩脉动，系统具有较好的动静态性能。

1 永磁同步电动机自适应反推直接转矩控制原理

永磁同步电动机在α-β两相静止坐标系中的电压方程：

(1)

式中：uα是定子电压在α轴上的分量；uβ是定子电压在β轴上的分量；Rs是定子电阻；iα是定子电流在α轴上的分量；iβ是定子电流在β轴上的分量；ωr是转子角速度；Ld是电感d轴分量；Lq是电感q轴分量；p是微分算子；θr是转子角度；ψf是转子永磁磁链；E为电机的反电动势。

根据式(1)可得到电流和磁链模型：

(2)

(3)

式中：ψα是定子磁链α轴分量；ψβ是定子磁链β是定子磁链β轴分量。

永磁同步电动机的电磁转矩方程、磁链方程、机械运动方程分别：

(4)

(5)

(6)

式中：Te是电磁转矩；ψs是定子磁链的平方；p是极对数；J是转动惯量；TL是负载转矩；Bm是粘滞摩擦系数。

在永磁同步电动机的直接转矩控制方法中，控制的目标是转速、转矩和磁链。定义转速跟踪误差：

(7)

选择eω为状态变量，转速误差导数根据式(6)可写作：

(8)

为了使速度跟踪误差趋于0，构造李雅普诺夫函数：

(9)

对Vl求导可得：

(10)

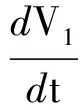
(11)

式中：ψsref为参考磁链的平方，则 ：

(12)

当kω>0时，通过李雅普诺夫稳定性分析可知，速度渐进跟踪，逐渐平稳。

在实际电机控制系统中，负载转矩TL是未知的，而且随着工作环境的变化定子电阻Rs和粘滞摩擦系数Bm也会变化，从而影响系统性能。因此将自适应控制和反推控制相结合，以达到改善这一状况的目的。

定义定子电阻误差ΔRs，粘滞摩擦系数误差ΔRm和负载转矩的估计误差ΔTL分别：

(13)

直接转矩控制中的核心控制量是电磁转矩和定子磁链，需要控制电磁转矩和定子磁链准确跟踪给定值，定义转矩误差eT和定子磁链eψ误差分别：

(14)

(15)

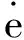
(16)

对于新的子系统，重新构造李雅普诺夫函数：

(18)

式中：γ1为定子电阻自适应增益；γ2为粘滞摩擦系数自适应增益；γ3为负载转矩自适应增益，且均为大于零的常数。

对式(18)求导，可得：

(19)

将式(15)、式(16)和式(17)代入式(19)中，并考虑到将自适应控制与反推控制相结合，取实际控制如下：

(20)

(21)

式中：kT，kψ分别为转矩和磁链调节系数，且均为大于0的常数。

将式(20)和式(21)代入式(19)，化简可得：

设计定子电阻，粘滞摩擦系数和负载转矩的自适应律：

(23)

把控制式(20)、式(21)和自适应律式(23)代入式(22)中，可得：

(24)

由于kω，kT，kψ均为大于0的常数，可使式(24)恒小于0，根据李雅普诺夫稳定性定律，则系统可以渐进稳定。

根据式(20)、式(21)和式(23)不仅可以使永磁同步电动机系统达到对转速、转矩和磁链的准确控制，还可以抑制定子电阻Rs、粘滞摩擦系数Bm和负载转矩TL的变化对系统性能的影响，从而保证系统具有较强的鲁棒性。

2 微粒子群算法优化自适应反推控制器参数

在自适应反推控制器中共有转速调节系数、转矩调节系数、磁链调节系数、定子电阻自适应增益、粘滞摩擦自适应增益和负载转矩自适应增益共6个可调参数，参数取值直接影响系统的性能。在这6个参数中磁链调节系数对系统性能影响较小，所以本文采用微粒群算法对自适应反推控制器的5个参数进行优化，即优化转矩调节系数kT、转速调节系数kω、定子电阻自适应增益γ1、粘滞摩擦自适应增益γ2和负载转矩自适应增益γ3。

微粒群优化算法是把个体看做N维搜索空间中的某一个微粒，这个微粒以一定的运行速度进行飞行。微粒与群体的速度会进行实时地调整，标准微粒群的速度更新方程：

(25)

式中：vj(t)是微粒j位于第t代的速度；w是惯性因子；c1是认知系数；r1是范围在(0，1)间的随机数；pj(t) 是微粒j的历史最优位置；xj(t) 是微粒j位于第t代的位置；c2是社会系数；r2是范围在(0，1)间的随机数；pg(t) 是群体历史最优位置。

由于pj(t)是微粒j的历史最优位置，对于目标为最小化为的控制系统而言，目标函数值越小，其对应适应值就越好，那么pj(t)更新规则：

(26)

而群体历史最优位置则定义：

(27)

式中：n为种群所包含的微粒个数。为了保证微粒群算法的稳定性，定义vmax为速度最大值，目的是以限制微粒j移动速度的快慢，即：

(28)

微粒j的进化方程：

(29)

根据式(25)设定微粒群优化中微粒的运行速度，由于w是一个非负数，对算法的性能影响很大，为避免出现局部最优值，本文采用逐渐递减公式：

(30)

式中：j为迭代第几次，nmax _length为最大迭代次数。这是因为随着迭代的进行，所取值逐渐接近最优值，同时微粒速度应随之减少。

认知系数c1和社会系数c2为一般正数或零，通常令c1=c2=2，r1和r2均为(0，1)分布的随机数，本文中微粒数n=30，微粒迭代次数N=40。

目标函数采用

(31)

如果出现超调则采用惩罚函数

(32)

式中：eω(t)为转速误差，tu为转速波形的上升时间，w1=103为权重系数。

基于微粒群优化的PMSM自适应反推DTC原理框图如图1所示。

图1 基于微粒群优化的PMSM自适应反推DTC原理框图

3 仿真结果分析

为了证明基于微粒群算法的自适应反推直接转矩控制方法的可行性和有效性，针对一台永磁同步电动机进行了仿真研究，同时也进行了传统直接转矩控制系统的仿真研究。仿真中的永磁同步电动机参数为：定子电阻0.2Ω；永磁体磁链0.24Wb；d轴电感8.5mH；q轴电感8.5mH；极对数为4；转子惯量1.23×10-3kg·m2。所得到的仿真结果如图2～图5所示。

图2是微粒群优化过程中kω和kT迭代选出最优值的走势调节图，星点表示每次迭代得到的历史最优值。从图2可以看出，两个参数取值在逐渐变化，在达到最大迭代次数之前，参数取值出现重叠，同时目标函数值达到最小，此时的参数即为kω和kT的最优值。图3是微粒群优化过程中γ1,γ2和γ3的取值走势图，星点表示每次迭代得到的参数历史最优值。从图3中可以看出，随着迭代次数的增加，参数取值逐渐改变，达到最大迭代次数时参数出现重合点，即参数取得最优值。最终通过PSO算法得出自适应反推控制器的调节参数：kω=955，kT=41399，kψ=1200。自适应增益：γ1=0.000009536，γ2=0.000 000 334，γ3=0.000 059 51。

图2 微粒群算法优化过程中kω和kT的取值走势

图3 微粒群算法优化过程中γ1，γ2和γ3取值走势

将微粒群优化算法得到的参数代入自适应反推控制系统中，当给定转速为1 000r/min空载起动稳定运行后，0.15s时负载转矩从0突增至2N·m情况下，传统直接转矩控制的仿真波形如图4所示，基于微粒群参数优化的自适应反推直接转矩控制系统的仿真波形如图5所示。从图4和图5可以看出，当转速给定为1 000r/min时，传统DTC和基于PSO的自适应反推DTC均可以达到给定转速，二者的起动时间相差无几。当电机稳定运行于1 000r/min，在0.15s时将负载转矩从0突增至2N·m时，转速始终稳定运行于1 000r/min，这说明基于微粒群优化算法的自适应反推DTC具有与传统DTC相同的动态响应性能。从传统DTC和基于PSO的自适应反推DTC的转矩和磁链波形可以看出，传统DTC存在着明显的转矩和磁链脉动，转矩脉动范围大约在±1N·m，而基于PSO的自适应反推DTC系统转矩和磁链脉动不明显。这是由于传统DTC磁链和转矩采用滞环控制，同时只在6个有效电压矢量和2个零矢量中选择最终电压矢量，所以存在明显的转矩和磁链脉动，而基于PSO的自适应反推DTC由于采用了空间矢量脉宽调制技术，可选电压矢量范围为任意大小和任意方向的电压矢量，所以转矩和磁链脉动明显减小。

(a)传统DTC转速波形(b)传统DTC转矩波形

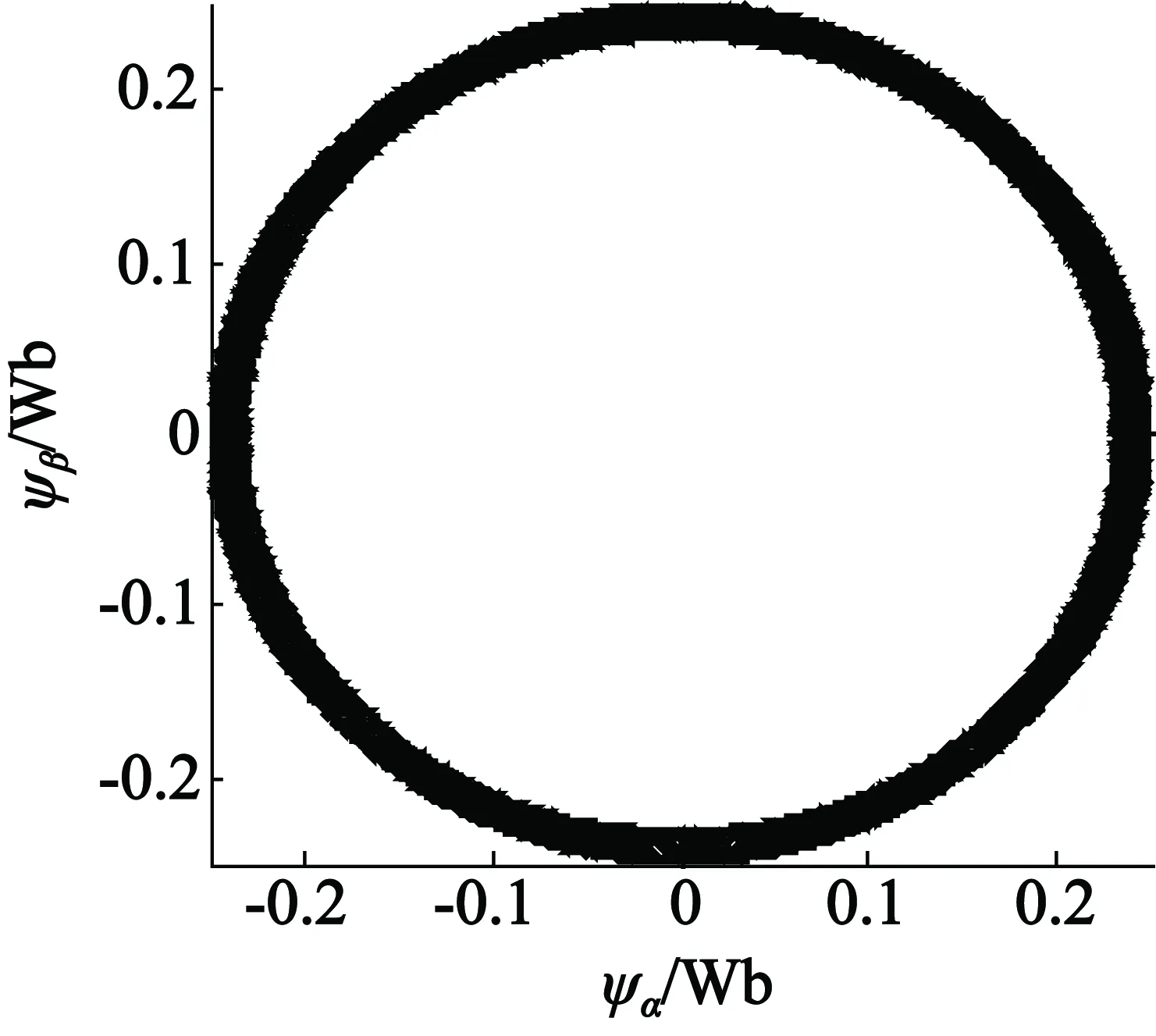
(c) 传统DTC转磁链波形

(a)基于PSO的自适应反推DTC转速波形(b)基于PSO的自适应反推DTC转矩波形

(c) 基于PSO的自适应反推DTC磁链波形

由上述仿真波形可以看出，采用微粒群算法可以优化出自适应反推控制器的参数，将优化出的参数代入到自适应反推DTC控制系统中，可以明显减小传统DTC系统中的转矩和磁链脉动，同时由于采用了空间矢量脉宽调制技术，也可使逆变器具有恒定的开关频率，由于自适应反推控制器存在多个可调参数，利用微粒群算法优化参数大大节省了调节参数的时间，对系统的实现具有重要意义。

4 结 语

本文针对永磁同步电动机传统直接转矩控制，提出了一种基于微粒群优化的自适应反推DTC方法，仿真结果证明了采用微粒群算法可以优化自适应反推控制器中的参数，与传统DTC方法相比，基于PSO的自适应反推DTC方法明显减小了磁链和转矩脉动，同时具有和传统DTC相同快速的动态响应，并使逆变器具有恒定的开关频率。由于自适应反推控制器方法中参数较多，难以调节，采用微粒群算法可以直接优化出参数，大大节省了系统调试时间，这对永磁同步电动机自适应反推直接转矩控制系统的实现具有重要意义。

[1]ZHONGL,RAHMANMF,HUWY,etal.Analysisofdirecttorquecontrolinpermanentmagnetsynchronousmotordrive[J].IEEETransactionsonPowerElectronics,1997,12(3):528-536.

[2]ZHONGL,RAHMANMF,HUWY,etal.Adirecttorquecontrollerforpermanentmagnetsynchronousmotordrives[J].IEEETransactionsonEnergyConversion,1999,14(3):637-642.

[3] 毛洁,周扬忠.永磁同步电动机反馈线性化控制系统设计研究[J].电力电子技术，2013,47(3):96-98.

[4] 孙晓东，朱熀秋．基于逆系统理论的永磁同步电动机解耦控制[J]．微电机，2009，42(4)：17-20.

[5] 刘栋良,郑谢辉,崔丽丽.无速度传感器永磁同步电机反推控制[J].电工技术学报，2011，26(9):67-72.

[6]MOCANUR,ONEAA.PassivitybasedtorquecontrolofPMSMusedinelectricalvehicles[C]//2015 19thInternationalConferenceonSystemTheory,ControlandComputing(ICSTCC),2015:803-810.

[7]ZHANGJinliang,KANGLongyun.Asensorlessvectorcontrolsystemofpermanentmagnetsynchronousmotorbasedonlineactivedisturbancerejectioncontroller[C]//InternationalConferenceonElectricalMachinesandSystem.IEEE,2015:1140-1144.

[8]NIUZhiwei,WANJianru,GEAng,etal.ResearchonslidingmodevariablestructurerotationalspeedobserverusedinPMSM-DTC[C]//2011 4thInternationalConferenceonPowerElectronicsSystemandApplication(PESA).IEEE,2011:1-5

[9] 杨俊华，吴捷，胡跃明.反步方法原理及在非线性鲁棒控制中的应用[J].控制与决策，2002，17(S1):641-647.

[10]REBOUHS,KADDOURIA,ABDESSEMEDR,etal.Adaptivebacksteppingspeedcontrolforapermanentmagnetsynchronousmotor[C]//2011InternationalConferenceonManagementandServiceScience.IEEE,2011:1-4

[11]RUDRAS,BARAIRK,MAITRAM,etal.Robustadaptiveintegralbacksteppingcontrolanditsimplementationonpermanentmagnetsynchronousmotor[C]//IEEEIndiaConference.IEEE,2012:1072-1077.

ResearchonAdaptiveBacksteppingDTCofPermanentMagnetSynchronousMotorBasedonParticleSwarmOptimization

XU Yan-ping,ZHANG Bao-cheng,ZHOU Qin,MA Ling-zhi

Becausetraditionaldirecttorquecontrol(DTC)methodhasdisadvantagesoflargefluxlinkageandtorqueripplesandhasinconstantswitchingfrequency,anadaptivebacksteppingDTCmethodbasedonparticleswarmoptimization(PSO)algorithmwasproposed.InthismethodanadaptivebacksteppingcontrollerforfluxlinkageandtorquewasdesignedaccordingtoDTCprinciplesofpermanentmagnetsynchronousmotor(PMSM)andthePSOalgorithmwasusedtooptimizeadaptivebacksteppingcontrollerparametersinordertoadjustthecontrollerparameters.SimulationresultsshowthatcontrollerparameterscouldbeoptimizedthroughthePSO,andcomparedtothetraditionalDTC,theproposedmethodcoulddecreasefluxlinkageandtorquerippleslargelyandmaketheinverterhaveconstantswitchingfrequency.

permanentmagnetsynchronousmotor;adaptivebacksteppingcontrol;particleswarmoptimization(PSO);directtorquecontrol

周慧(1987-)，男，硕士研究生，研究方向为电机控制。

2015-12-10

国家自然科学基金项目(51107098)

TM341;TM

A

1004-7018(2017)01-0062-05

(Xi’anUniversityofTechnology,Xi’an710048,China)