航路飞行航空器冲突风险建模与灵敏度分析

李冰冰

(中国民航大学 空中交通管理学院，天津 300300)

● 基础科学与技术 Basic Science & Technology

航路飞行航空器冲突风险建模与灵敏度分析

李冰冰

(中国民航大学 空中交通管理学院，天津 300300)

航空器间冲突风险建模与分析是飞行冲突识别和评估的关键技术。以同航路不同高度层飞行的航空器为研究对象，考虑分别应用纵向/侧向/垂直间隔标准以及水平/垂直间隔标准两种情况，基于概率分析方法分别建立不同高度层飞行航空器间的冲突概率模型，并分别进行相对标称位移、间隔标准以及位置误差标准差对冲突概率影响的灵敏度分析；以航空器间相对标称位移变化趋势为基础，通过引入航空器间冲突风险严重度指数，进一步给出航空器间冲突风险模型。数值仿真算例验证了冲突风险建模与分析方法的可行性，以及灵敏度分析结论的准确性。

安全评估；航路飞行；冲突概率；冲突风险；灵敏度分析

近年来，我国民航业发展势头迅猛，对于空域的需求不断增加。对于空域的各种优化调整，必须通过方案的安全评估才可应用于实际。因此，当今迫切需要开展新技术条件下空域规划方案的安全性评估方法研究，才能有针对性地逐步优化现有空域资源配置，提高空域运行管理水平。

从国外空域规划方案安全性评估分析方法历史来看，1966年，Reich模型奠定了飞行间隔安全评估基础[1]；2011年，Luís Campos等人利用广义概率分布模型评估同航路或平行航路的冲突风险概率，更加准确地评估了冲突概率[2]；FedjaNetjasov发表的3篇系列论文研究了空域重组和扇区划设新方案下，巡航空域安全评估的总冲突风险模型建构；李冰冰通过冲突风险模型，建立以及管制员工作负荷的预测进行扇区规划的安全评估[3-4]。

国内方面：1991年，张林昌等研究了雷达监视下程序管制的最小航路宽度和雷达引导时的飞机侧向安全间隔问题[5]；徐肖豪等研究了空管二次雷达的最小间隔的分析与比较[6]；李冬宾等针对不同的航路结构，构建了各种碰撞风险计算模型[8-10]。其他领域对于碰撞概率也有较深入的研究，值得借鉴。2008年，白显宗等人基于压缩空间和坐标旋转的碰撞概率计算方法，探讨了空间目标碰撞概率的计算[11]；2013年，张健等人提出了基于误差分析的潜艇碰撞概率的计算模型，揭示交会过程中潜艇碰撞概率与各个交会参量之间的关系[12]。

本文在前人研究的基础上，利用随机过程的相关知识，根据建立的坐标系，建立同航路不同高度层下的冲突概率计算模型，并进行两机相对标称位移、位置误差标准差以及不同垂直水平间隔标准对于冲突概率影响的灵敏度分析。首次引入冲突严重度的概念，根据冲突严重度以及冲突概率，确定任一相对距离下两机冲突风险，建立基于风险的安全评估体系，通过算例验证该模型的实用合理性。

1 航空器间冲突概率建模

1.1 模型假设

(1)航空器标称航迹沿航路中心线；

(2)相对于航空器标称位置存在纵向、侧向和垂直3个方向的位置误差分量，相互独立且服从零均值正态分布；

(3)不同航空器的位置误差分量之间相互独立；

(4)任意时刻，航空器的实际位置可表示为标称位置向量与位置误差向量之和；

(5)航空器沿航路和指定高度层自主独立地飞行，无人为干预。

1.2 相对位置分量

空域(扇区)内存在不同方位的多条航路，为了清晰描述航路方位和航空器的具体位置，建立扇区整体参考坐标系(OXYZ)I和航路坐标系(OXYZ)R(如图1所示)。

图1 相关坐标系

某时刻，在航路坐标系中，位于同航路不同高度层的两架航空器i和j的位置坐标可分别描述为

式中：e为位置误差分量，下标x，y，z分别为纵向、侧向和垂直3个方向。

两航空器之间的相对位置向量为

由于上述相对位置向量的各分量均为正态分布随机变量的线性组合，根据正态分布有关性质可知，各个分量也是彼此相互独立的正态分布随机变量，即

上述关系式中，当ΔZij=0时，表示两航空器在同一高度层飞行。

1.3 纵向/侧向/垂直间隔标准情况

对于同航路飞行的两航空器，在分别应用纵向、侧向和垂直间隔标准时，只有当两航空器同时在纵向、侧向和垂直等3个方向不满足对应的间隔标准Sx，Sy和Sz时，两航空器才发生冲突，即冲突条件可表述为

|ΔXij|≤Sz，|ΔYij|≤Sz，且|ΔZij|≤Sz

考虑到航空器相对位置分量间的独立性，两航空器间冲突概率可表示为

Pij=P{(|ΔXij|≤Sx)∩(|ΔYij|≤Sy)∩(|ΔZij|≤

Sz)}=P{|ΔXij+Δexij|≤Sx}·P{|Δeyij|≤

(1)

式中：

分别为航空器间纵向冲突概率、侧向冲突概率和垂直方向冲突概率；而函数Φ(·)为标准正态分布函数。

1.4 水平/垂直间隔标准情况

对于同航路飞行的两航空器，在分别应用水平和垂直间隔标准时，需要将水平方向的相对位置分量综合起来加以考虑，将[ΔXijΔYij]T视为相互独立的二维正态随机变量，其概率密度函数为

同样，定义只有当两航空器同时在水平、垂直两个方向不满足对应的间隔标准Sxy和Sz时，两航空器才发生冲突，即冲突条件可表述为

(2)

式中：

分别为两航空器间水平和垂直方向的冲突概率。

1.5 航空器间冲突风险建模

两机冲突风险严重度指数是建立在辨识两机冲突可能造成的后果类型及其阈值的基础上的，可反映任一时刻下两机冲突的风险水平。在任一时刻下，用一个参数来表示两机冲突的风险水平，即风险严重度指数。

2013年，中国民航局发布的《民用航空器事故症候》[13]中，对于航空器小于规定间隔事件的危险指数评价方法做出了规定。当发生小于规定间隔事件时，危险指数通过累加的方法进行计算，即危险指数为垂直间隔、水平间隔、接近率、航迹夹角与人员状态的危险指数之和。当危险指数≥90时，为运输航空严重事故症候，当危险指数在75(含75)到89(含89)之间时，为运输航空一般事故症候。

本文主要研究两机冲突风险随两机纵向相对标称位移的变化趋势，其他因素暂不考虑。根据相关理论数据以及国内外经验，本文认为，相遇后的风险指数应小于相遇前同等标称距离下的风险指数，并且随着离开相遇点的距离越远，风险指数的减小速度越快。参考《民用航空器事故症候》对于水平间隔危险指数的规定，本文定义两机在相遇前和相遇后的冲突风险严重度指数(S)见表1。

表1 基于纵向相对标称距离的两机冲突风险严重度指数(S)

按照安全风险管理的思想，风险应该等于危险发生概率与其严重度的乘积。本文1.4节已经得到两机冲突概率的表达式，1.5节定义了风险严重度指数随纵向相对标称位移的变化趋势(见表1)，则同航路不同高度层下两机冲突风险等于两机冲突概率与两机冲突风险严重度的乘积，即两机冲突风险Rij为

Rij=Pij×Sij

2 冲突概率灵敏度分析

航空器间冲突概率大小和变化趋势不仅依赖于其相对标称位移分量，而且依赖于不同方向的间隔标准和航空器随机位置标准差等参数。为此，定义航空器间冲突概率相对这些分量或参数的单位变化率为对应的冲突概率灵敏度。

2.1 相对标称位移的影响分析

沿航路方向航空器间冲突概率Pxij对于相对标称位移Δxij的灵敏度为

当Δxij=0时灵敏度等于零；当Δxij>0时灵敏度小于零，说明随着Δxij的增大冲突概率在减小，同时注意到Pxij关于Δxij的对称性。可知：当纵向相对标称距离|Δxij|的值增加时，冲突概率将变小，呈现出负相关关系，也就是说，两航空器间距离越大，冲突概率将越小。类似的结论对垂直方向冲突概率也同样成立。

2.2 间隔标准的影响分析

沿航路方向航空器间冲突概率Pxij对于纵向间隔标准Sx的灵敏度为

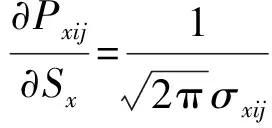
由上式可知，纵向间隔标准的增加会增加两航空器间沿航路方向的冲突概率，两者呈正相关关系，类似的结论对另外两个方向的冲突概率也同样成立。

2.3 位置误差标准差的影响分析

沿航路方向航空器间冲突概率Pxij对于位置误差分量的标准差σxij的灵敏度为

(3)

为判定上述灵敏度函数的正负，给定一组参数，上述关于标准差σxij的灵敏度函数随Δxij的典型变化曲线如图2所示。

图2 标准差的灵敏度函数随相对标称位移的典型变化曲线

令灵敏度函数式(3)等于零，并令Δxij=Sx+δx，得

(4)

利用数值方法求解得到使式(2)成立的δx。由图2可知：当0≤xij≤Sx+δx时(可称为标称冲突范围)，式(1)一定小于零，说明此时随着标准差的σxij增加，冲突概率会减小，呈负相关关系；但当xij>Sx+δx时，式(3)又大于零，说明随着标准差σxij的增大，冲突概率也会增大，呈正相关关系。

侧向冲突概率对于标准差σyij的灵敏度为

3 算例分析

3.1 算例描述

假设管制区内某航路长度L=200 km，如图3所示为沿该航路相邻高度层反向飞行的两航空器i和j，两机地速均为vi=vj=800 km/h；假设初始时刻t=0，两架航空器同时进入航路。

假设两机相对标称位置的随机误差标准差、纵向/侧向/垂直间隔标准以及水平间隔标准分别为

σxi=3 km，σyi=2 km，σzi=60 m；

σxj=3 km，σyj=2 km，σzj=60 m；

Sx=10 km，Sy=10 km，Sz=300 m；Sxy=10 km

图3 两机i，j飞行示意

上述输入参数可以作为基础值，用于参数变化后的冲突概率灵敏度分析比较和验证。

3.2 冲突概率灵敏度分析

首先，分析两航空器冲突概率随纵向相对标称距离|ΔXij的变化。通过计算得到两航空器冲突概率随相对标称位移变化曲线如图4所示。

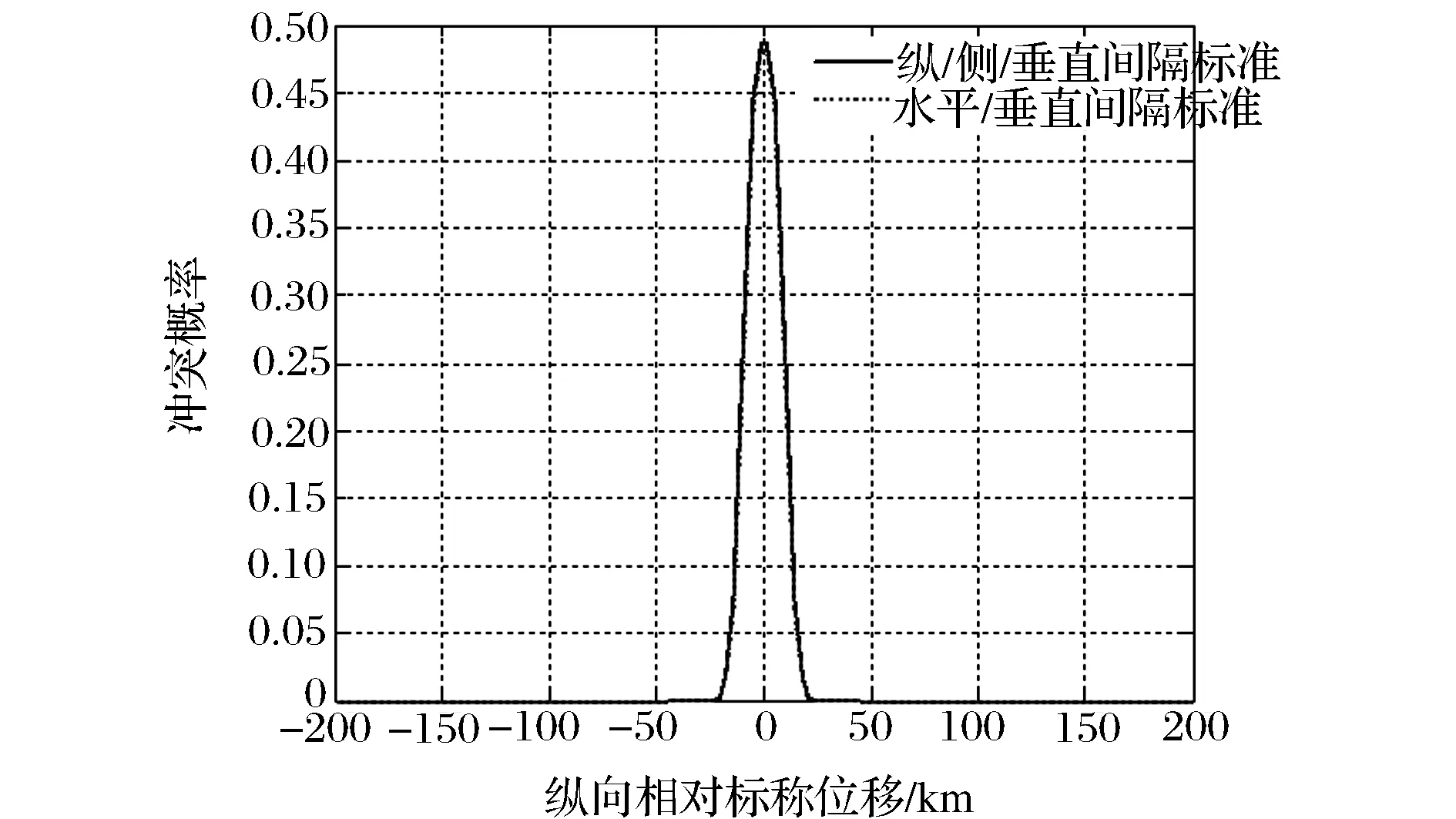
图4 两机冲突概率随纵向相对标称位移变化曲线

由图4可知：当两机刚进入航路时，随着纵向相对位移的减小，冲突概率逐渐增大，当两机相对位移为0时，两机冲突概率最大，接近0.5，达到最接近的相遇状态；经过相遇点之后，两机相对距离又逐渐拉大，两机冲突概率也随之减少。说明两机冲突概率随纵向相对标称距离|ΔXij|的增大而减小，呈现负相关关系。此外可以看出，采用冲突概率模型(1)和(2)得到的结果非常接近，两条曲线几乎重合。其次，分析冲突概率随间隔标准的变化趋势。为此，保持算例其余参数不变，设定另一组新的增大的间隔标准：

Sx=20 km，Sy=20 km，Sz=300 m；Sxy=20 km

分别针对两组参数情况，得到不同间隔标准情况下冲突概率时间历程比较曲线如图5所示。

图5 不同间隔标准情况下两机冲突概率时间历程比较曲线

由图5可看出，在同一时刻，采用较大间隔标准的冲突概率明显大于较小间隔标准的冲突概率。同时，还可发现采用较大间隔标准时，两机处于高概率冲突阶段的持续时间也较长。算例结果表明，间隔标准与两机冲突概率呈正相关关系。 最后，分析冲突概率对于位置标准差的变化趋势。为此，保持算例其余参数不变，设定另一组新的增大的位置标准差：

σxi=5 km，σyi=4 km，σzi=60 m；

σxj=5 km，σyj=4 km，σzj=60 m。

分别计算两组参数情况下的冲突概率，得到不同标准差情况下的时间历程比较曲线如图6所示。图6中，“△”标识的曲线表示采用较小的标准差情况的冲突概率变化曲线，无标识的表示采用较大标准差情况。由图6可知：在t=7.5 min(相遇时刻)附近，大标准差情况的冲突概率明显小于较小标准差情况的冲突概率，标准差出现负相关的关系；而在该范围以外，大标准差情况的冲突概率又大于较小标准差情况的冲突概率，呈现正相关的关系。

图6 不同标准差情况下两机冲突概率时间历程比较曲线

由图4～图6中还可发现，采用纵向/侧向/垂直间隔标准(实现所表示的线型)与采用水平/垂直间隔标准(虚线所表示的线型)计算出的冲突概率非常接近，两条曲线基本重合，说明两种冲突概率模型计算结果一致。

3.3 冲突风险分析

针对3.1节算例，基于冲突概率模型和定义的冲突严重度指数，采用1．5节建立的冲突风险模型，得到两航空器在相遇时刻t=7.5 min附近的冲突风险如图7所示。

图7 冲突风险随纵向相对位移的变化曲线

由图7可知，冲突风险在两机到达相遇点前后的变化是不对称的。在同样的相对标称距离下，相遇前的冲突风险要比相遇后要大，说明两机在相遇之前具有较大的冲突严重度指数，而在相遇之后具有较小的冲突严重度。在相遇范围内，两机冲突风险达到最大，最大的冲突风险值在相遇点附近持续一段时间。

4 结 论

(1)分别建立的采用纵向/侧向/垂直间隔标准和采用水平/垂直间隔标准下航空器间冲突概率模型，两者的计算结果高度一致。

(2)冲突概率的灵敏度分析结果表明，两机冲突概率与间隔标准呈正相关关系，与相对标称距离呈负相关关系；当两机处于标称冲突范围内，冲突概率与位置标准差呈负相关关系；但当两机在标称冲突范围以外时，呈正相关的关系。

(3)基于冲突概率模型，并引入与两机接近趋势相关的基于纵向相对位移的冲突风险严重度指数，建立了冲突风险模型。所建立的航空器间冲突概率和冲突风险模型可以用于航空器冲突评估，也可延展应用于整个扇区的冲突风险评估。

[1] REICH P G. Analysis of long range air traffic systems : separation standards III[J]. Journal of the Institute of Navigation ,1966 ,19 (1) :88-98 .

[2] LUíS Campos. Collision Probabilities, Aircraft Separation and Airways Safety[J].Aeronautics and Astronautics, 2011(12):571-588.

[3] FedjaNetjasov.Framework for airspace planning and design based on conflictrisk assessment Part 1: Conflict risk assessment model for airspace strategic planning[J]. Transportation Research Part C,2012 (24):190-212.

[4] FedjaNetjasov.Framework for airspace planning and design based on conflictrisk assessment Part 3: Conflict risk assessment model for airspace operational and currentday planning[J]. Transportation Research Part C ,2013 (32):31-47.

[5] 张林昌,王守兴. 我国航路监视下横向间隔标准的确定方法[D].北京:北京航空航天大学,1991.

[6] 徐肖豪,马子兴,聂润兔.空管二次雷达最小间隔的分析与比较研究[J].交通运输工程与信息学报,2004(1):87-92.

[7] 李冬宾,徐肖豪,李雄.基于不同航路构型的空中碰撞风险模型研究[C]//中国自动化学会控制理论专业委员会.第二十七届中国控制会议论文集.北京:中国自动化学会控制理论专业委员会,2008:4.

[8] 孟祥伟,张平,王瑛. 交叉航路航空器碰撞风险评估[J].北京航空航天大学学报, 2010(9): 1021 -1025.

[9] 韩松臣,曲玉玲. 航路交叉点处碰撞风险模型[J].西南交通大学学报, 2013(2): 383-389.

[10] 黄卫芳. 浅谈我国空域仿真评估[J].中国民用航空,2008(9):25-26.

[11] 白显宗,陈磊.空间目标碰撞预警中的碰撞概率问题研究[D].长沙:国防科学技术大学,2008.

[12] 张健,万正权,尹群.潜艇碰撞概率计算方法研究[J].中国造船,2012,53(4):137-145.

[13] 中国民用航空局. 2001—2013民用航空器事故症候:MH/T[S].中国: 中国民用航空局,2013.

(编辑：史海英)

Aircraft Conflict Risk Modeling and Sensitivity Analysis of En-route

LI Bingbing

(Air Traffic Management College, Civil Aviation University of China, Tianjin 300300, China)

Modeling of conflict risk between aircrafts is the key technology of flight conflict identification and evaluation. Considering the two status of longitudinal/lateral/vertical separation minima and horizontal/vertical separation minimum, the paper establishes conflict probability models of aircrafts in different flight level with probability analysis method respectively, and analyzes the sensitivity of impact of relative displacement, separation minima and position error on conflict probability. It also presents conflict risk model between aircrafts by introducing conflict risk severity index based on changing trend of relative displacement between aircrafts. The numerical simulation case verifies the feasibility of conflict risk modeling and analysis method and the accuracy of sensitivity analysis result.

security evaluation; en-route flight; conflict probability; conflict risk; sensitivity analysis

2016-08-23；

2016-11-18．

李冰冰(1990—)，女，硕士研究生.

10.16807/j.cnki.12-1372/e.2017.02.022

V328.1

A

1674-2192(2017)02- 0090- 06