钢质管道弯曲破坏时材料曲线的确定试验

杨 培，李 昕，高 杰，周 晶

(大连理工大学建设工程学部，辽宁 大连 116024)

钢质管道弯曲破坏时材料曲线的确定试验

杨 培，李 昕，高 杰，周 晶

(大连理工大学建设工程学部，辽宁 大连 116024)

依据ASTM-A370-13规范，对API 5L X52无缝管道钢进行了单轴拉伸试验。得到了不同取样形式下拉伸试样的应力-应变关系曲线，据此分析拉伸试样取样形式对材料特性的影响规律。利用数值仿真软件ABAQUS，以得到的材料应力-应变关系曲线作为有限元计算输入曲线，对复杂荷载作用下X52管道全尺寸弯曲破坏试验进行数值模拟并与试验结果进行对比。结果表明：采用轴向圆棒试样对应的材料曲线得到的数值计算结果与试验结果吻合最好，该取样形式下的材料曲线可以更加准确地表达钢质管道弯曲破坏时的材料特性。

拉伸试验； 应力-应变曲线； 管道钢； 取样形式； 弯曲破坏试验

1 引 言

海底管道处于恶劣的海洋环境中，常常受到内压、外压、轴向力、剪力、弯矩，扭矩等荷载联合作用。国内外学者[1-6]通过理论分析、模型试验和数值模拟对海底管道在联合荷载作用下的失效机理和极限承载力进行了研究。在研究中，管材本构关系是影响管道极限承载力的关键因素，如何通过材料单轴拉伸试验得到准确的材料本构关系对研究工作的成功至关重要。

国内外学者在金属材料拉伸试验影响因素方面进行了一些研究。Kyriakides和Corona[7]研究了钢材材料强度与加载应变率之间的关系。张方举等[8]通过试验测定了V-5Cr-5Ti合金在不同应变率下的拉伸性能。李国强等[9]通过Q345钢的恒温加载和恒载升温单轴拉伸试验，得到了高温钢材料模型。胡文军等[10]研究了温度对V-5Cr-5Ti合金拉伸性能及组织结构的影响。马鹏程、王迎等[11-12]则研究了加工工艺对铝镁合金力学性能的影响。以上作者给出了拉伸试样的外部环境对金属材料力学性能的影响规律。在管道钢拉伸试样取样形式方面，国内外现有拉伸试验标准[13-15]等都规定了多种取样形式。如全尺寸轴向试样、轴向矩形试样、轴向弧形试样、轴向圆棒试样、环向矩形试样和环向圆棒试样等。但在如何选取拉伸试样取样形式方面各标准并没有给出指导性意见。因此，本文从拉伸试样取样形式的角度对管道弯曲破坏时材料曲线的确定进行了试验研究。

首先通过材料单轴拉伸试验得到了不同取样形式拉伸试样的材料曲线，给出了取样形式对材料特性的影响规律。然后进行了复杂荷载作用下管道的全尺寸弯曲破坏试验，利用数值仿真软件ABAQUS对破坏试验进行数值模拟进而确定管道钢材料拉伸试验时最

合理的取样形式，这对管道钢材料的单轴拉伸试验具有一定的借鉴意义。

2 材料单轴拉伸试验

拉伸试样母材为API 5L X52[16]无缝钢质管道，共计6根，分别用 X52#1—X52#6标识。管道标称外径356mm，标称壁厚9mm，长3000mm。拉伸试样采用“X52#X-Y”标识，其中X为管道编号，如上所述，Y为取样形式编号，取S1、S2、S3、S4，分别表示轴向矩形试样、轴向弧形试样、轴向圆棒试样和环向圆棒试样，如图1所示。从#1和#6管道上切取S1、S2、S3型拉伸试样，从#2和#5管道上切取S1、S3型拉伸试样，从#3和#4管道上切取S1、S3、S4型拉伸试样，各类型拉伸试样均为2根。表1给出了拉伸试样的实际几何尺寸。

图1 拉伸试样示意图Fig.1 Shapes of tensile specimens

ItemLDBCGRW(d)tS125690751850131259S22628907518502512510S31850805010356875875S4853522616544

由于轴向弧形试样具有初始曲率，而试验机夹具为扁平夹头，为防止试样从夹头滑落，在进行拉伸试验前对试样两端部进行了冷压平处理。拉伸试验在CSS电子万能试验机上进行，采用引伸计和静态电阻应变仪来测量变形和应变。试验加载方式采用位移控制，十字头的自由运行速率为2mm/min。

材料单轴拉伸试验结果如表2所示。表中偏差为其他取样形式试样试验结果相对于轴向矩形试样的偏离程度。从表中可以看出弹性模量E的分布随机性较大。随着取样形式的变化，材料的屈服强度sy和工程极值强度st的变化规律基本一致，即环向圆棒试样所得结果最大，轴向圆棒试样次之，轴向矩形和弧形试样所得结果基本一致且最小。虽然各取样形式下拉伸试样的试验结果存在偏差，但偏差程度均不是很大。由此可见，拉伸试样取样形式对材料特性的影响程度有限。

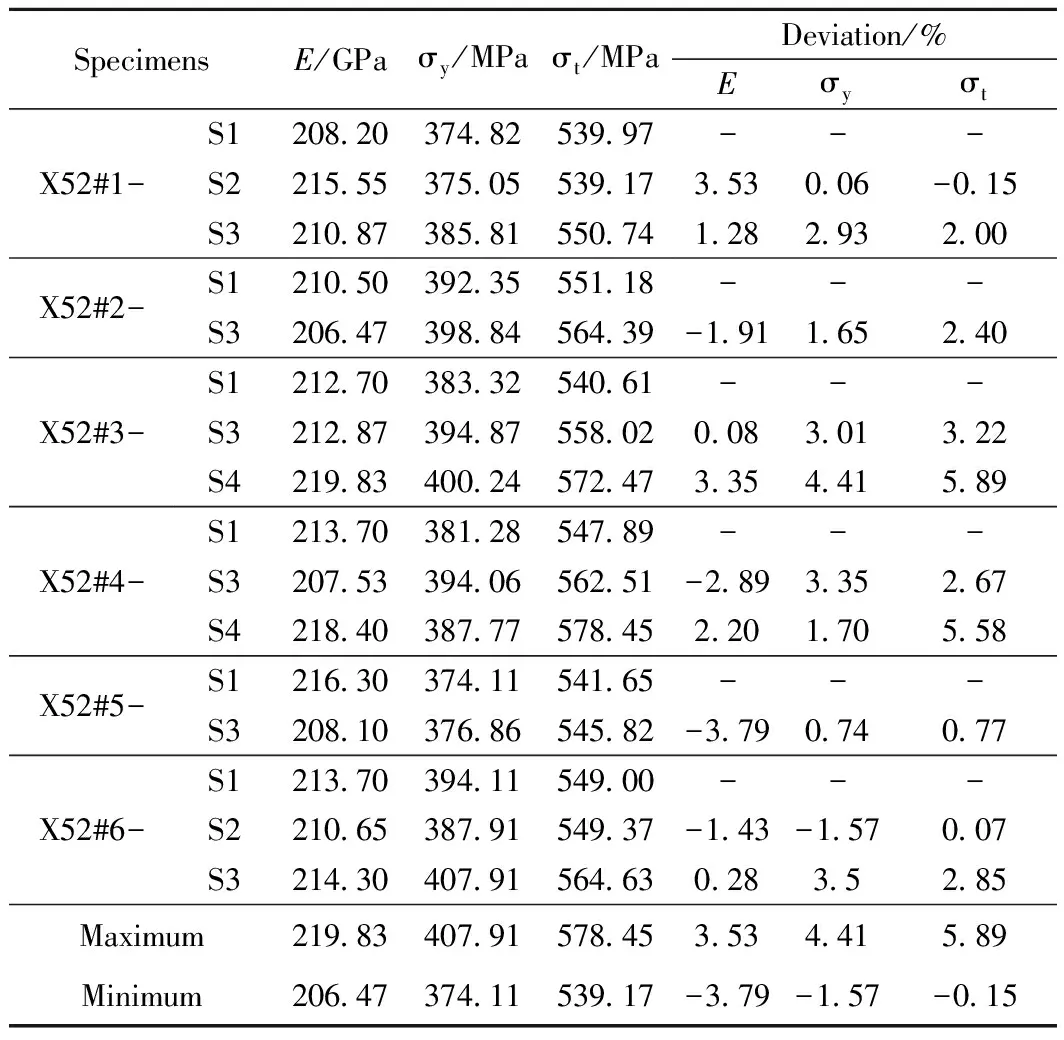
表2 X52管道钢拉伸试验结果(平均值)

注：通过试验发现取样形式对材料泊松比几乎无影响，这里统一取ν=0.28

拉伸试验已得到材料的工程应力-应变曲线，根据式(1)和式(2)可得到X52#6管道钢的真实应力-应变曲线，如图2所示，该曲线将作为下文数值计算用的材料本构关系输入数据。可以看出，轴向圆棒试样应力-应变曲线在屈服和强化阶段要略高于轴向矩形和轴向弧形试样。

(1)

(2)

式中：σtrue为真实应力；εnom为真实应变；σnom为工程应力；εnom为工程应变。

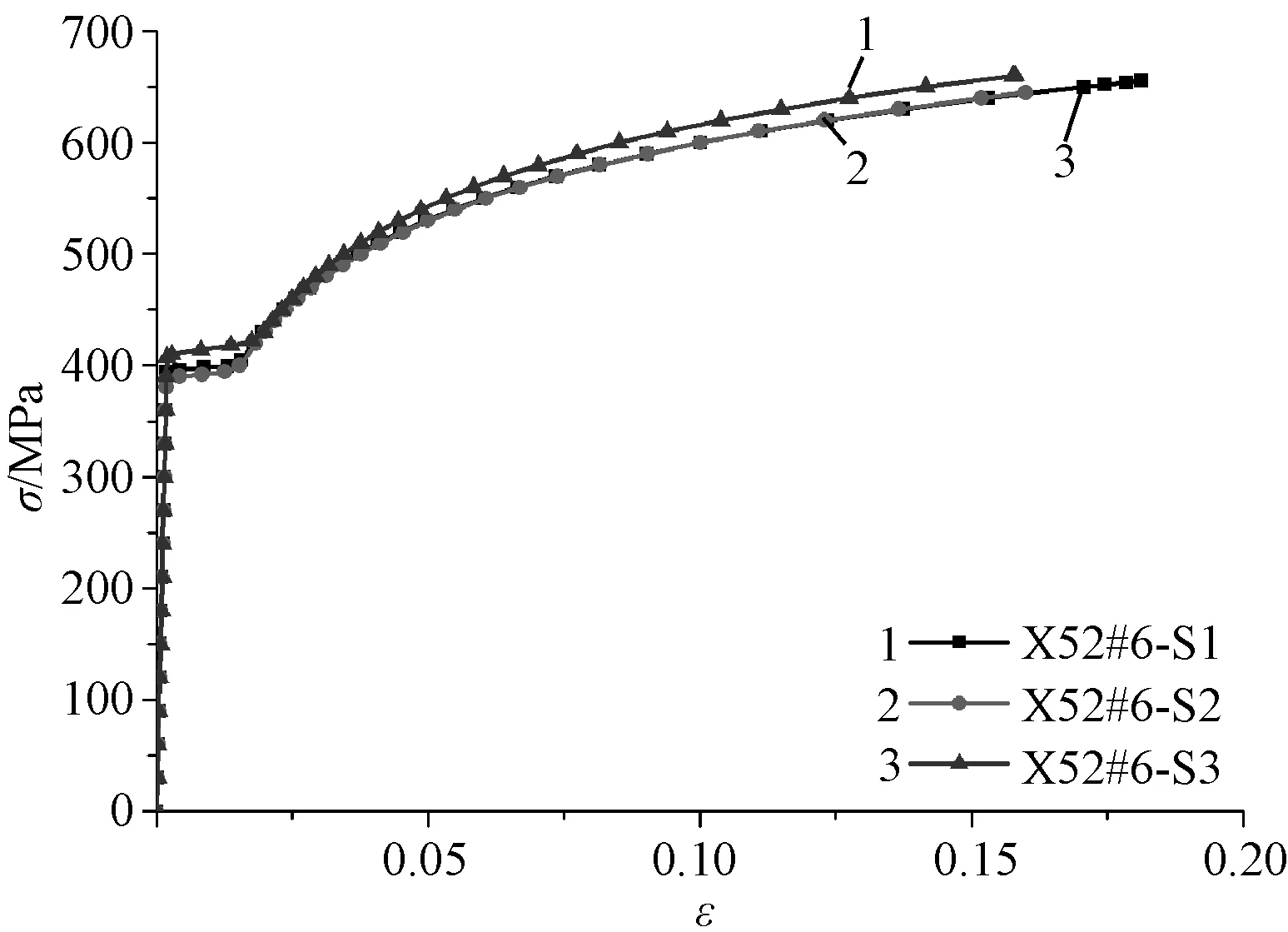
图2 X52#6管道钢真实应力应变曲线(平均值)Fig.2 X5 2#6 steel true stress-strain curves (averaged)

3 管道全尺寸弯曲破坏试验

以X52#6管道为试验管道，长2620mm，该长度大于管道直径的3倍，可以保证局部屈曲的发展且不受边界条件的影响[1]。在试验管道两端部110mm范围内采用加强钢板将端部与法兰盖焊接，以避免局部屈曲发生在端部区域。

由于海底管道与周围土体的摩擦作用，管道常常受到由管道内外温差引起的轴力Pα和泊松效应引起的轴力Pν作用。此外，试验管道两端与法兰盖焊接成封闭系统，内压作用在封闭端对管道产生轴向拉力，该拉力在实际两端开口的管道中并不存在，因此需要在管道端部施加轴向压力PP以抵消该拉力的影响,各轴向力计算公式如下所示。

(3)

(4)

(5)

式中，“+”表示拉力，“-”表示压力，A为管道横截面面积，E为材料弹性模量，α为材料热膨胀系数，ΔT为管道内外温差，ν为泊松比，σh为环向应力，ri为管道内半径，p为内压。

破坏试验研究在45℃温差下无内压管道的极限弯矩承载力。已知α=11.7E-06/℃，弹性模量E通常取207GPa，则施加在管道上的总轴力为：

P=Pα+Pν+Pp=-1092+0+0=-1092kN

(6)

管道全尺寸弯曲破坏试验在复杂荷载动静试验机[17]上进行。该试验机可以对管道施加内压、轴力和弯矩的任意组合荷载，模拟油气输送管道真实的受力环境，并能够自动采集试验过程中的载荷、位移、变形等数据。试验时，首先对管道施加轴向压力1092kN，然后采用轴力不变加载方式对管道进行弯矩加载，直至管道破坏。在该加载方式下，管道所受轴力在整个弯矩加载过程中始终保持不变。弯矩加载是通过位于弯曲梁之间的弯曲油缸施加的反向轴力对管道端部产生力矩的形式实现的。试验过程中管道始终在由弯曲梁及管道中心轴线所在的平面内变形。

4 数值分析

4.1 有限元模型

考虑到直径、壁厚等初始几何缺陷对复杂荷载作用下管道的极限弯矩承载力影响相对较大[18]，故使用管道几何尺寸测量机[19]测量了管道直径和壁厚数据，其分布情况如图3、4所示。从图中可以看出试验管道的直径离散程度较小，壁厚离散程度较大，其中环向165°方向壁厚较小，将其作为管道弯曲破坏试验的中心受压侧。

图3 管道直径分布Fig.3 Distribution of diameters

图4 管道壁厚分布Fig.4 Distribution of wall thickness

采用ABAQUS建立全尺寸有限元分析模型，如图5所示。该模型包括两部分：(1)试验管道，含初始几何缺陷，采用8结点六面体线性减缩积分单元C3D8R；(2)弯曲梁及法兰盖，采用4结点四面体线性单元C3D4。试验时弯曲梁与法兰盖采用螺丝紧固，建模时可将两者视为整体。模型两端设置参考点RP-1和RP-2，参考点与弯曲梁的转轴采用Coupling约束，管道端部与法兰盖采用tie约束。试验管道会产生较大的塑性变形，其网格密度对数值收敛有很大影响，经过初步的网格密度收敛性分析确定管道网格密度为2层(径向)×96份(环向)×176份(轴向)。弯曲梁和法兰盖的刚度较大，只需进行适当的网格划分即可保证足够的计算精度。

图5 有限元模型Fig.5 Finite element model

4.2 材料模型

X52#6管道钢材料模型为各向同性的弹塑性模型，采用Von Mises 屈服准则及对应的塑性流动法则，并遵循等向强化规律。对于管道两端部110mm长的加强区，认为其材料参数与原管道钢一致，考虑为线弹性模型，这样就可以保证端部不发生塑性变形，从而避免端部位置局部屈曲的产生[1]。弯曲梁及法兰盖采用线弹性模型，其材料的弹性模量E=209GPa，泊松比ν=0.27。

4.3 边界条件及荷载

试验过程中管道在轴向(Z)自由伸缩，在弯曲平面内(XOZ)变形。因此，施加在参考点RP-1、RP-2的边界条件为：RP-1，U1=U2=U3=UR1=UR3=0；RP-2，U1=U2=UR1=UR3=0。其中U1、U2、U3分别为沿X、Y、Z轴的平动自由度，UR1、UR2、UR3分别为绕X、Y、Z轴的转动自由度。荷载分两个加载步加载：轴力加载步，在RP-2点加载轴向压力F1=1092kN；弯曲力加载步，在弯曲力作用点加载反向弯曲力F2，并在RP-2点加载相同大小的F2，以抵消弯曲力对管道轴力的影响。

4.4 结果分析

采用Full Newton法对轴力加载步进行非线性分析，采用改进的Riks法对弯曲力加载步进行非线性分析，分析试验加载工况下管道的反应。非线性分析考虑了管道的大位移、大变形、几何非线性及材料非线性。

图6为管道平均端部弯矩-整体曲率关系的数值结果与试验结果的对比。最初管道的弯矩承载力与整体曲率之间为线性关系，随着弯曲变形的增加，管道逐步进入屈服，并出现应变硬化和椭圆化现象。材料的应变硬化促使管道弯矩承载力进一步增加至最大值。随着弯曲变形的进一步增加，椭圆化变形开始占主导地位，致使管道的弯矩承载力缓慢下降。最后，管道达到临界屈曲状态，超过临界状态后管道的弯矩承载力急剧下降，管道屈曲破坏。可以看出，平均端部弯矩—整体曲率曲线的有限元值与试验值在弹性段吻合很好，在塑性段各曲线开始出现不同程度的分离。其中，采用轴向矩形和轴向弧形试样对应的材料曲线得到的有限元结果相近，但均与试验结果存在较大的偏差。采用轴向圆棒试样对应的材料曲线得到的有限元结果与试验结果吻合很好，说明轴向圆棒试样对应的材料曲线相对而言能够很好地反映X52#6管道钢在弯曲破坏时的材料特性。表3列出了不同材料曲线下数值计算结果与试验结果的偏差。从中可知采用X52#6-S3材料曲线得到的各数值计算结果与试验结果的最大偏差仅为-4.15%。

图6 数值结果与试验结果比较Fig.6 Comparison between numerical resultsand test results

PositionMaterialcurvesUltimatemomentpointCriticalbucklingpointMoment/kN·mDeviation/%Globalcurvature/rad·m-1Deviation/%Moment/kN·mDeviation/%Globalcurvature/rad·m-1Deviation/%Testresults43724-00265-39298-00720-X52#6⁃S140286-78600241-90637453-46900773736X52#6⁃S239502-96600230-132137178-53900759542X52#6⁃S342195-35000254-41538712-14900736222

5 结 论

通过材料单轴拉伸试验得到了不同取样形式拉伸试样的材料曲线。利用得到的材料曲线对管道的全尺寸弯曲破坏试验进行数值模拟并与试验结果对比得出以下结论：

1. 拉伸试样取样形式对材料屈服强度及工程极限强度的影响具有规律性，而对弹性模量的影响显示出较大的随机性。

2.轴向圆棒试样对应的材料曲线能够更加准确地表达钢质管道弯曲破坏时的材料特性。因此建议采用轴向圆棒拉伸试样来获得管道钢材料的本构关系。

出于经济因素，本文所进行的单轴拉伸试验的试样数量有限，但还是能够在利用拉伸试验确定管道钢的材料曲线方面给出一个客观的试验结果，这对管道钢材料单轴拉伸试验具有一定的借鉴意义。

[1] Mohareb M, Kulak G L, Elwi A, Murray D W. Testing and analysis of steel pipe segments [J]. Journal of Transportation Engineering, 2001, 127(5): 408～417.

[2] Ozkan I F, Mohareb M. Moment resistance of steel pipes subjected to combined loads[J]. International Journal of Pressure Vessels and Piping, 2009, 86: 252～264.

[3] Ozkan I F, Mohareb M. Testing and Analysis of Steel Pipes under Bending, Tension, and Internal Pressure[J]. Journal of Structural Engineering, 2009, 135(2): 187～197.

[4] Sфren R H, Bai Y. Bending Moment Capacity of Pipes[J]. Journal of Offshore Mechanics and Arctic Engineering, 2000, 122: 243～252.

[5] Mohareb M. Plastic Interaction Relations for Pipe Sections[J]. Journal of Engineering Mechanics, 2002, 128(1): 112～120.

[6] 党学博,龚顺风,金伟良,等. 深水海底管道极限承载能力分析[J]. 浙江大学学报 (工学版),2010, 44(4): 778～782.

[7] Kyriakides S, Corona E. Mechanics of Offshore Pipelines Volume 1: Bucking and Collapse[M]. First edition ed. Slovenia: Elsevier BV, 2007, 361～363.

[8] 张方举,胡文军,谢若泽,等. 应变率对V-5Cr-5Ti合金拉伸性能的影响[J]. 材料科学与工程学报,2010, 28(4): 536～539.

[9] 李国强,陈凯,蒋首超,殷颖智. 高温下Q345钢的材料性能试验研究[J]. 建筑结构, 2001, 31(1): 53～55.

[10] 胡文军,潘晓霞,陈勇梅,牛伟,王彤伟. 温度对V-5Cr-5Ti合金拉伸性能及组织结构的影响[J]. 材料科学与工程学报,2011, 29(4): 564～568.

[11] 马鹏程,张迪,庄林忠,张济山. 冷轧工艺及退火温度对AL-Mg合金组织和性能的影响[J]. 材料科学与工程学报, 2014, 32(6): 792～797.

[12] 王迎,潘清林,彭虹,李晨,陈琴,尹志民. 退火温度对铝镁钪合金力学和腐蚀性能的影响[J]. 材料科学与工程学报, 2012, 30(6): 913～918.

[13] 金属材料拉伸试验第1部分:室温试验方法[S]. GB/T 228.1-2010.

[14] Standard Test Methods and Definitions for Mechanical Testing of Steel Products[S]. ASTM-A370-13.

[15] Standard Test Methods for Tension Testing of Metallic Materials[S]. ASTM-E8/E8M-13a.

[16] Specification for Line Pipe[S]. API SPECIFICATION 5L.

[17] 李昕,周晶,朱彤,苏晨亮,高杰. 一种复杂荷载试验机[P]. 中国. ZL 201320629244.7. 2014-04-09.

[18] 王慧平,李昕,周晶. 初始几何缺陷对管道极限承载力影响研究[J]. 海洋工程, 2014, 32(5): 50～56.

[19] 李昕,高杰,周晶. 一种管道几何尺寸的测量机[P]. 中国. ZL 201320559041.5. 2014-02-12.

Experimental Research on Determination of Material Curve of Steel Pipe during Bending Failure

YANG Pei， LI Xin， GAO Jie， ZHOU Jing

(Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China)

Uniaxial tensile tests of API 5L X52 seamless pipeline steel were carried out according to ASTM-A370-13 standard. The stress-strain curves of the tensile specimens of different shapes were obtained, and the influence of the specimen shape on the material properties was analyzed. Using the stress-strain curves obtained above, the full scale bending failure test of the X52 pipeline under complex loads was simulated by ABAQUS. The numerical results were compared with the experimental results. It shows that the numerical results obtained by using the stress-strain curve of longitudinal round specimen are in good agreement with the experimental results. It can be concluded that the stress-strain curve of the longitudinal round specimen is more accurate to represent the true material properties of steel pipe during bending failure.

tensile tests； stress-strain curve； pipeline steel； shapes of specimens； bending failure test

1673-2812(2017)01-0134-05

2015-10-26；

2015-12-30

国家重点基础研究发展计划(973计划)资助项目(2011CB013702)

杨 培(1989-)，男，硕士研究生，研究方向:钢结构。E-mail：1051871269@qq.com。

周 晶，教授，E-mail：zhouj@dlut.edu.cn。

TE973

A

10.14136/j.cnki.issn 1673-2812.2017.01.027