基于主成分分析和神经网络相结合的制冷剂充注量故障诊断

袁玥，陈焕新，石书彪，郭亚宾，黄耀

（1-华中科技大学中欧清洁与可再生新能源学院，湖北武汉 430074；2-华中科技大学能源与动力工程学院，湖北武汉 430074）

0 引言

在能源资源日渐枯竭的今天，如何提高能源效率、降低能耗成为了一个具有重要意义的研究课题。目前，制冷空调系统占建筑系统总能耗的比例高达30%～45%[1]，有效地降低空调能耗、提高制冷空调的工作效率便可以降低能耗，提升能源利用率。

制冷空调系统的故障检测和诊断（Fault Detection and Diagnosis，FDD）是在综合考虑系统测量数据、控制执行信号、运行模式等参数的基础上，构建数学或者物理模型，判断和识别系统所处工作状态的一种方法和技术[2]。故障诊断的初级目标是判断系统整体或局部是处于正常状态抑或是故障状态；进一步的目标是在判定系统处于故障状态之后，识别系统故障发生的源头、找出其故障发生的原因[3]；最终目标是提前预测故障发展走势，实现故障预警，甚至避免故障的发生，保证制冷空调系统平稳高效运行。

制冷剂充注量是影响制冷系统性能的重要参数之一，若发生故障没有及时排除，会导致系统能耗增加、设备寿命缩短、人员体感不适甚至影响正常的工作[4]。为了更好地减低能耗，减小不必要的资源浪费，提高室内环境舒适度[5]，如何对制冷剂充注量进行准确高效的故障诊断就成为了一个亟待解决的问题。

目前，故障诊断的方法大致可分为以下3种[6]：基于知识的故障诊断方法，基于解析模型的故障诊断方法，基于数据驱动的故障诊断方法。在基于知识的方法中，张杰等[7]对专家系统和神经网络在故障诊断中的应用做出了详细的介绍。基于模型的方法中，包括状态估计法、参数估计法等等。其方法对于线性系统的研究比较透彻，而对于非线性系统则相对较弱。基于数据驱动处理的方法中，回避了建立准确数学模型的难点，对于线性和非线性系统都具适用性[8]。WANG等[9]首先提出主元分析法应用于制冷空调行业的故障诊断领域中；王志毅等[10]利用小波变换的方法成功对空调热负荷增大这一故障进行了分析。王江宇等[11]利用主成分分析-决策树（Principal Component Analysis and Decision Tree，PCA-DT）的方法对多联机制冷剂充注量进行了故障检测与诊断，该方法对于多联机（Variable Refrigerant Flow，VRF）的制冷剂充注量故障有良好的检测与诊断效果。GUO等[12]提出一种卷积-主元分析的方法，与传统的主成分分析方法相比，这种方法可以显著地提高多联机系统故障检测及诊断的精度。LIU等[13]利用PCA-DT方法对VRF系统进行了在线故障检测及诊断，结果表明，PCA-DT方法比仅使用决策树的算法有更优的诊断结果，并且具有良好的鲁棒性。

从大量数据中挖掘有效信息，发现规律的数据挖掘算法是如今应用较为广泛的故障诊断方法。其中，多层前馈（Back Propagation，BP）神经网络是目前使用颇为成熟的数据挖掘算法之一，其推理过程实质是模拟大脑思维结构进行数值计算过程，避免了专家系统诊断过程中出现的“匹配冲突”、“无穷递归”等问题[14]。但是直接利用BP神经网络进行故障诊断具有网络权值难以理解、容易陷入局部极小值、网络稳定性差且收敛速度较慢、泛化能力也会较弱[15]等等缺陷，所以须与其他方法结合使用。

将PCA与BP神经网络相结合，既可以除去原始信息中的冗余部分，降低输入数据维数，又可以发挥BP神经网络非线性建模的能力，提高模型的泛化能力和学习稳定性[16]。

本文利用收集到的多联机冷水机组实测制冷剂充注量数据，提出一种基于PCA-BP神经网络制冷剂充注量故障检测与诊断的方法，选择进行MATLAB建模，进行制冷剂充注量工作状态的研究，结果证明该算法有良好的检测与诊断结果。

1 PCA-BP故障诊断模型

1.1 主元分析法

主元分析法[17]（PCA）又被称作是主成分分析法。它是一种利用矩阵分析降维处理数据，将多个特征转化为少数几个指示性更强的特征的多元统计方法[18]。提取出来的变量与初始数据集的关系如图2所示。将数量较多而且相关关系不明确的若干个变量变为数量较少而且互不相关的主成分变量。

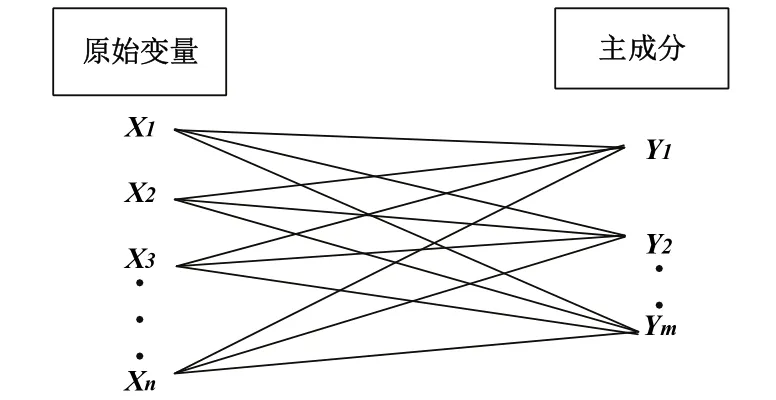
图1 原始变量与主成分之间的关系

PCA的实现过程可以描述为[19]：原始采样数据集经过标准化归一化之后变成标准矩阵X，X∈Rm×n，其中，每一列代表一个特征，每一行代表一个观测样本。将X的协方差矩阵R作为主元分析的对象。

对协方差矩阵R进行特征值分解，分别得到了对应的特征值和特征向量。每个特征向量称之为一个主元。将特征值按从大到小的顺序依次排列，所对应的特征向量也依次排列组成特征值矩阵U。

定义第k个主元的贡献率（Contribution of Variation）为该主元对应的特征值比上总特征值之和[20]。

定义第k个主元的累计贡献率（Cumulative Contribution of Variation）为前k个主元的特征值之和除以总特征值之和。

当累计贡献率大于等于85%[17]时，此时的前k个主元可以组成新的矩阵作为统计分析的判据。

1.2 BP神经网络

BP神经，又称为多层前馈神经网络，是一种近年来应用广泛且发展迅速的一种人工神经网络。其拓扑结构包括：输入层、若干隐含层和输出层。其中，隐含层作为实现映射的主要功能单元。在该网络中，只有上下层级关系的神经元之间存在映射，而同层的神经元之间没有耦合。因此，BP神经网络的传递具有单向性[21]。

BP神经网络的算法分为两部分：第一步：正向传播，输入信号从输入层通过隐含层逐层计算输出值，如果输出层没有得到想要的输出结果，则继续进行第二步；第二步：反向传播，输出误差逐层向前算出隐含层单元的误差，由这个误差勘正前面层级的权值[22]。BP神经网络是前馈式神经网络最核心最精华的部分[23]。

在BP神经网络中，隐含层数及其节点数的确定还没有一个标准的方法。如果选取节点数过少，不足以产生足够数目的连接权组合数来使神经网络对样本进行学习，易造成神经网络性能不佳甚至不能训练的状况；如果选取节点数过量，则可能由于训练时间过长而导致陷入局部极小点而达不到最优点[24]。

关于隐含层节点数的确定，有若干经验公式[25]，本文选用的如公式(4)所示。

其中，n为输入节点数，m为输出层节点数。

早在1989年，HECHT-NIELSEN[26]已经证明了三层结构的神经网络模型可以逼近仿真任何非线性问题。故在本文中，也采用三层神经网络结构。

1.3 PCA-BP神经网络模型构建

虽然BP神经网络具有泛化能力强、精度高等等优点，但是网络训练精度与训练时长受到样本间相关性、样本容量以及网络结构的制约。把PCA与BP神经网络相结合，除去过于冗余的变量，BP神经网络处理信息的能力将会变得更加优秀。

首先通过PCA对数据进行降维分析，得出主要影响成分作为神经网络新的学习样本空间。然后将新的学习样本作为BP神经网络的输入层，并进一步构造神经网络的预测模型。这样以来，不仅简化了神经网络的结构，而且节约了计算空间，使之兼具有神经网络的学习能力和鲁棒性，既满足了精度要求，又降低了神经网络输入层的复杂程度，很好地提高了学习速率。

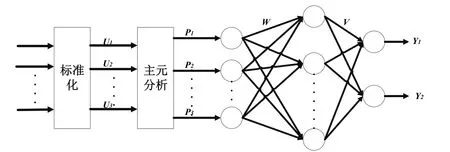
图2 PCA-BP模型结构

2 实验数据来源

2.1 实验数据采集

实验数据来源于某多联机制冷充注量实验，多联机的结构图如图3所示，该机组由5台室内机和1台室外机组成[27]。

如表1所示，共有9种不同的制冷剂充注量水平，在制冷剂充注量为65%～80%时，判定为制冷剂充注量不足；在制冷剂充注量为85%～110%时，判定为制冷剂充注量正常；在制冷剂充注量为120%～130%时，为制冷剂充注量过量。

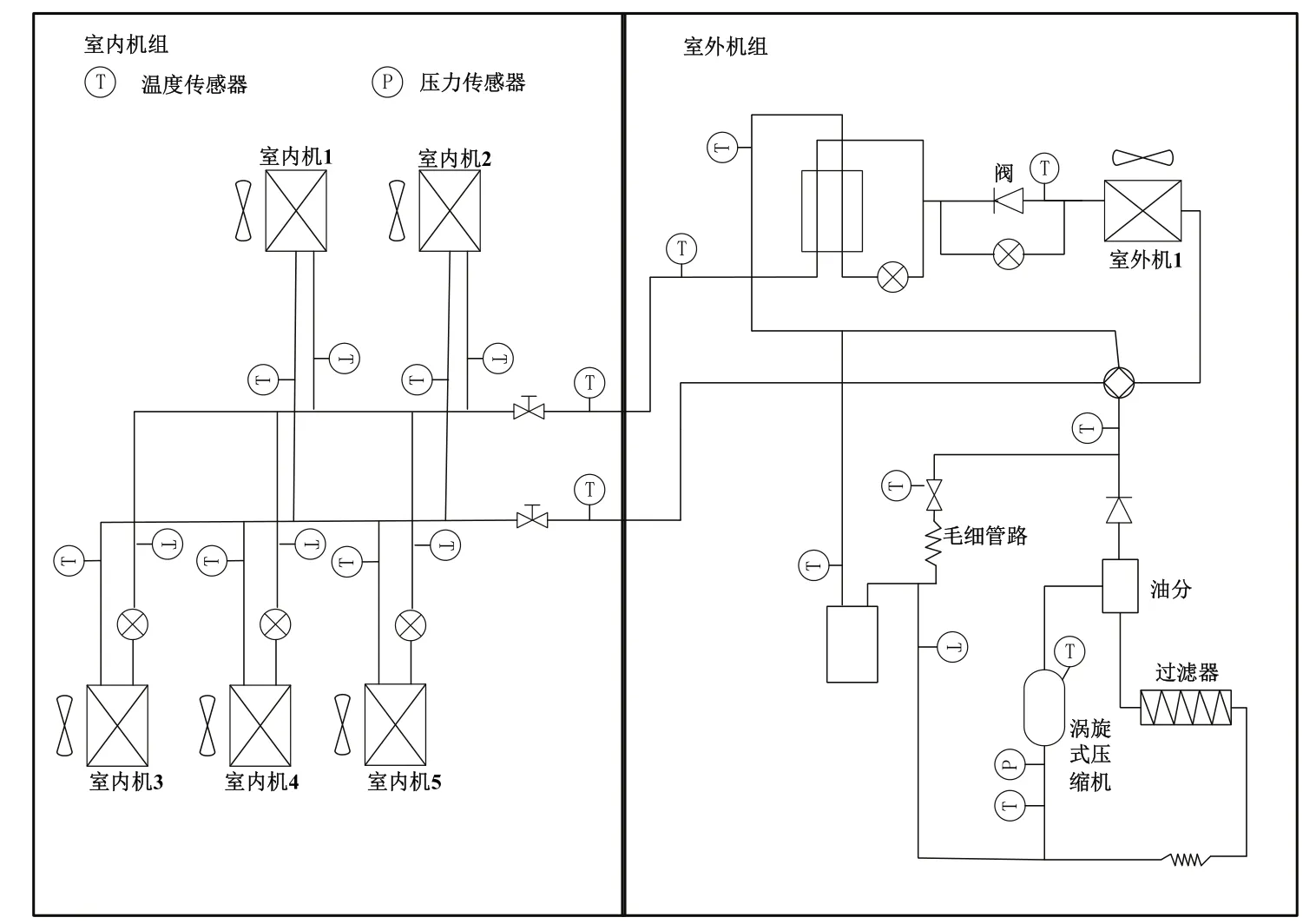
图3 多联机制冷充注量实验示意图

表1 制冷剂充注量水平

2.2 实验数据预处理

在对多联机进行实际数据采样的过程中，由于其采样间隔短、时间长、测量点较多、数据量较大等因素影响，数据集中存在一些缺失值、不变值，会导致后期算法运行时间周期长、效率低下。为保证数据质量，避免这些现象的发生，故对原始数据进行数据预处理。其过程包括：剔除数据中数值保持不变的死值变量以及温度、压力等变量中超出正常范围的测量值。最终选取表2中22个特征变量进行后续工作并且将添加制冷剂充注量充注情况作为其标签列。

3 故障检测与诊断结果分析

3.1 模型构建

PCA-BP方法的基本思路，如图4所示。先利用PCA对原有的制冷剂充注量实验数据进行降维处理，得到降维之后的数据，再利用BP神经网络进行训练，对降维后的网络数据进行故障检测与诊断。

表2 特征变量

该数据共有18,065个样本，根据主元分析法得到了23个主元的贡献率及累计贡献率如表3所示，因此，选取前8个累计贡献率为89.85%（大于85%）的主元作为主成分，进行故障检测工作。同时从表中可得知，前7个主元与前8个主元的累计贡献率差别很小。

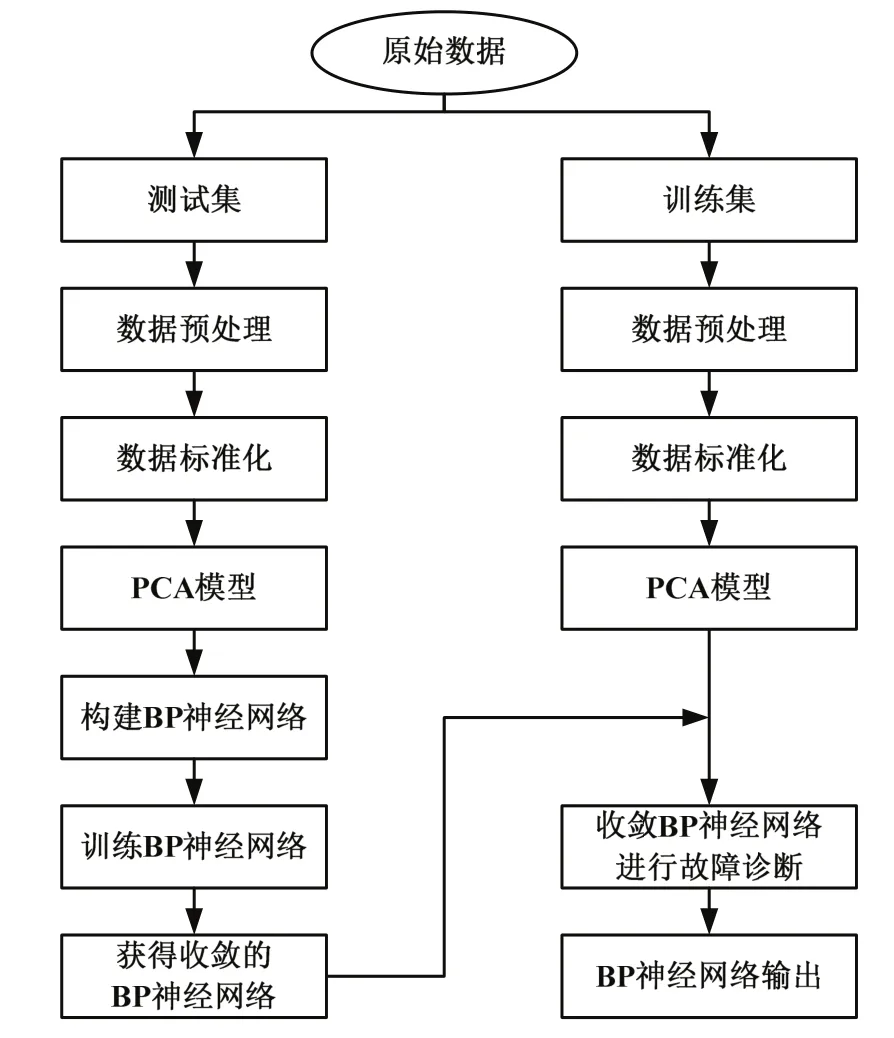
图4 基于PCA-BP神经网络的诊断流程

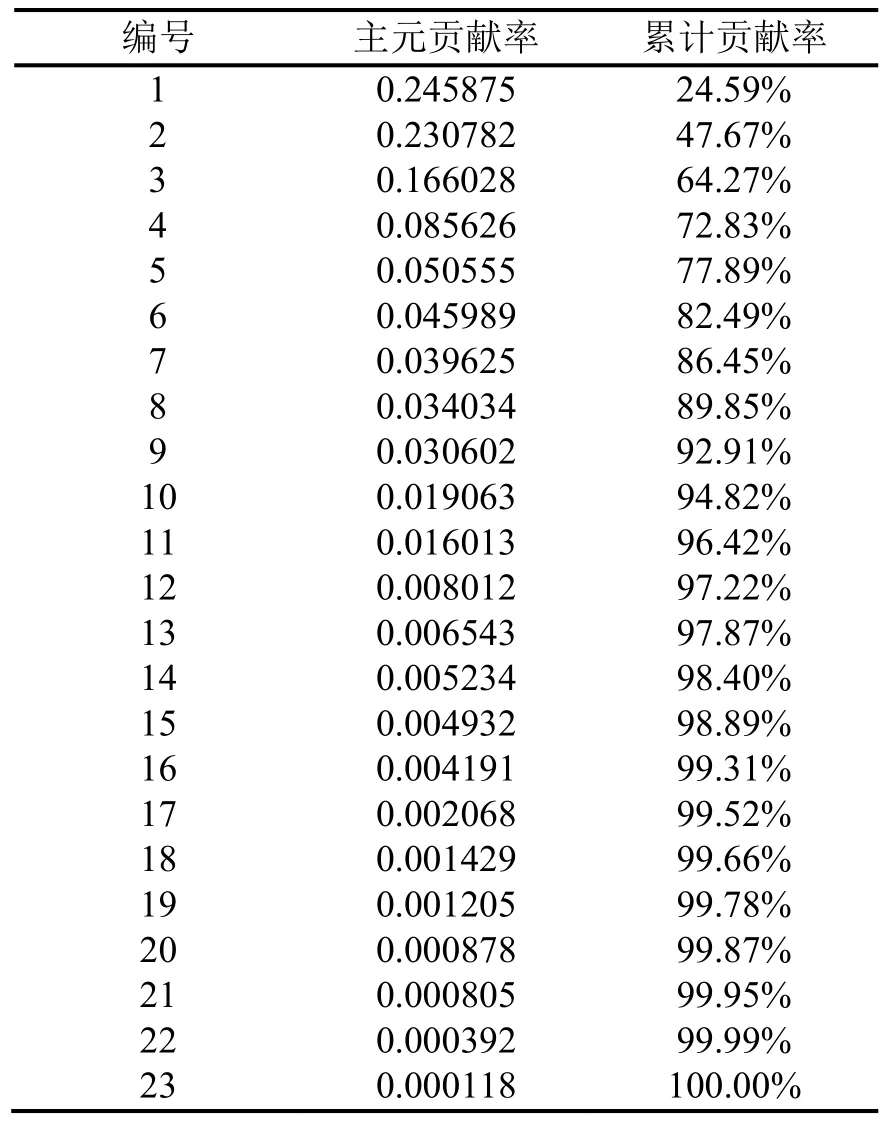
表3 主元贡献率及累计贡献率

根据PCA主元分析的结果选取了前8个特征向量作为输入层，经仿真结果验证，当隐含层节点数为17，确定为一个8-17-3的三层神经网络时，取得最佳预测效果。

输出层采用制冷剂充注不足、制冷剂充注正常、制冷剂充注过量3个变量作为输出神经元，分别对应编号A1，A2，A3，神经网络输出分别为（1 0 0）、（0 1 0）、（0 0 1）。即共有3类标签，输出层有3个节点数（见表4）。

输入层与隐含层传递函数为tansig，隐含层到输出层之间的传递函数为logsig。由于问题的复杂性不太大，为了保证系统的稳定性，故选取学习速率为0.01；最大训练次数设为1,000次，训练样本最小均方误差设为0.00004，其他参数均选用默认值，运用MATLAB R2015b对样本进行训练和预测。

当迭代到第541次时，训练样本满足最小均方误差要求，网络达到稳定的状态。

表4 3个特性向量指示编号

3.2 仿真结果

由表5可知，由PCA-BP神经网络方法得到的制冷剂充注量预测结果与实际情况相比，诊断的正确率在97%以上，结果较为理想，收敛速度也很快。

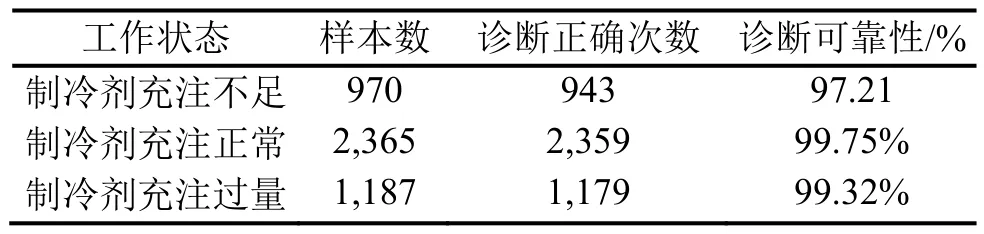
表5 PCA-BP制冷剂充注量测试结果

为了进一步说明PCA-BP神经网络与传统BP神经网络方法相比具有独特的优越性，用传统BP神经网络进行训练，与PCA-BP神经网络的结果进行对比。在各个参数均不变的情况下，分别对比在样本个数为181、362、1,807、3,016和18,064的情况下，测试的时间长度以及充注量诊断的正确率的对比结果如表6所示。

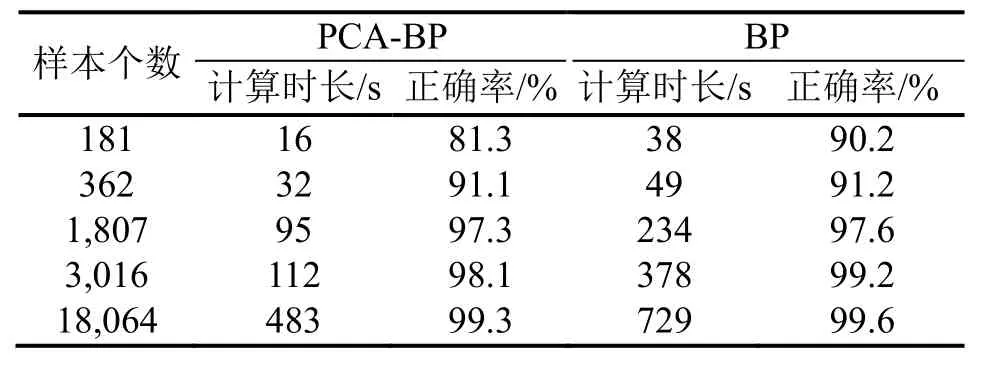
表6 制冷剂充注量的诊断时长与正确率比较

从表格可以看出，当样本个数到达一定数量之后，相较于传统BP神经网络且PCA-BP神经网络在与之正确率相差不大的情况下，在节约训练时间长度以及平均迭代次数上优势明显，具有更好的泛化能力。

4 结论

BP神经网络具有并行计算能力和非线性处理能力，对于故障检测及诊断问题有良好的适用性，但其也具有较容易陷入局部极小和收敛速度较慢等缺陷。如果将采集得到的数据进预处理后，先采用PCA减少输入向量的维数对BP神经网络加以改进，则能够使神经网络的输入层很好地完成线性组合，极大地简化网络并缩短训练时间。该方法对于制冷剂充注量故障有良好的诊断精度，同时也具有一定的泛化能力，可以推广到多联机其他故障的诊断中。

引入PCA对样本进行降维处理，消除了特征之间的相关性，大大加快了神经网络的收敛速度，同时也较为明显地提高了故障诊断精度。

对于输入维数较多的原始数据，可以考虑采用该种PCA-BP算法，将会极大地缩短训练和测试的时间，同时也保留了BP神经网络对于制冷剂充注量故障诊断良好的准确性。但是也需注意由BP神经网络的参数设置具有多样性所带来的问题，应该成为后续研究学习的一个重点方向。

[1]劳文慧. 空调节能技术分析[J]. 制冷, 2002, 21(1):79-80.

[2]倪健斌, 余晓明, 陈丽娜. 某商场中央空调系统现场测试及故障分析[J]. 制冷技术, 2006, 26(4): 33-36.

[3]陈焕新, 孙劭波, 刘江岩, 等. 数据挖掘技术在制冷空调行业的应用[J]. 暖通空调, 2016, 46(3): 20-26.

[4]王少雄. 制冷故障排除经验谈[J]. 制冷技术, 1994,14(3): 18.

[5]陈玲, 杜志敏, 晋欣桥, 等. 压缩机性能试验台的测控可靠性研究[J]. 制冷技术, 2016, 36(3): 24-32.

[6]陈焕新, 刘江岩, 胡云鹏, 等. 大数据在空调领域的应用[J]. 制冷学报, 2015, 36(4): 16-22.

[7]张杰, 高宪军, 姚劲勃, 等. 基于神经网络与专家系统的故障诊断技术[J]. 吉林大学学报信息科学版, 2009,27(3): 319-323.

[8]任能. 制冷系统故障检测、诊断及预测研究[D]. 上海:上海交通大学, 2008.

[9]WANG S, XIAO F. AHU sensor fault diagnosis using principal component analysis method[J]. Energy and Buildings, 2004, 36(2): 147-160.

[10]王志毅, 谷波, 黎远光. 小波变换应用于空调制冷机组故障先兆预测[J]. 暖通空调, 2004, 34(10): 117-120.

[11]王江宇, 陈焕新, 刘江岩, 等. 基于PCA-DT的多联机制冷剂充注量故障诊断[J]. 华中科技大学学报(自然科学版), 2016, 44(7): 1-4.

[12]GUO Y, LI G, CHEN H, et al. An enhanced PCA method with Savitzky-Golay method for VRF system sensor fault detection and diagnosis[J]. Energy and Buildings, 2017,142: 167-178.

[13]LIU J, LI G, CHEN H, et al. A robust online refrigerant charge fault diagnosis strategy for VRF systems based on virtual sensor technique and PCA-EWMA method[J].Applied Thermal Engineering, 2017, 119: 233-243.

[14]HABERL J. S, CLARIDGE D. E. An expert system for building energy consumption analysis: prototype results[J]. ASHRAE Transactions, 1987, 93: 979-998.

[15]SHANG C, CHEN X, QIAN J. A soft-sensing model built for acetic acid distillation columns based on the PCA-BP neural network[J]. Industrial Instrumentation and Automation, 2003(4): 33-36.

[16]刘增明, 陈运非, 蒋海青. 基于PCA-BP神经网络方法的供应商选择[J]. 工业工程与管理, 2014, 19(1): 53-57.

[17]LEIGH S. A User's Guide to Principal Components[J].Journal of the Operational Research Society, 1992, 43(6):641-641.

[18]WANG S, XIAO F. AHU sensor fault diagnosis using principal component analysis method[J]. Energy and Buildings, 2004, 36(2): 147-160.

[19]胡云鹏. 基于主元分析的冷水机组传感器故障检测效率研究[D]. 武汉: 华中科技大学, 2013.

[20]WANG S, FU X. Detection and diagnosis of AHU sensor faults using principal component analysis method[J]. Energy Conversion and Management, 2004, 45(17): 2667-2686.

[21]张义宏. 基于PCA的BP神经网络优化的研究与应用[D]. 沈阳: 东北大学, 2014.

[22]石书彪, 陈焕新, 李冠男, 等. 基于改进BP网络的冷水机组故障诊断[J]. 制冷学报, 2015, 36(6): 34-39.

[23]王战魁. 基于PCA与BP神经网络的危险化学品车辆识别[D]. 北京: 首都经济贸易大学, 2006.

[24]王灿进, 孙涛, 石宁宁, 等. 基于双隐含层BP算法的激光主动成像识别系统[J]. 光学精密工程, 2014, 22(6):1639-1647.

[25]沈花玉, 王兆霞, 高成耀, 等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报, 2008, 24(5): 13-15.

[26]HECHT-NIELSEN R. Theory of the backpropagation neural network[C]// International Joint Conference on Neural Networks. IEEE, 1989: 593-605.

[27]SHI S, LI G, CHEN H, et al. Refrigerant charge fault diagnosis in the VRF system using Bayesian artificial neural network combined with ReliefF filter[J]. Applied Thermal Engineering, 2016, 112: 698-706.