差分数据处理技术在形变监测中的应用
王东东,黄智刚,秦红磊,梁 宵
(北京航空航天大学 电子信息工程学院,北京 100191)
差分数据处理技术在形变监测中的应用
王东东,黄智刚,秦红磊,梁 宵
(北京航空航天大学 电子信息工程学院,北京 100191)
针对GNSS差分技术在实际应用中存在数据结果跳变、稳定度低、定位精度差的问题,采用野值检验与修正、正态分布检验和高稳定度数据分析的方法,研究实现差分数据的高精度、高稳定度处理。实验结果能够证明方法的可行性和有效性,可为GNSS高精度差分定位应用的推广提供借鉴。
数据处理;形变监测;全球卫星导航定位;高稳定度;高精度
0 引言
全球卫星导航系统(global navigation satellite system,GNSS)高精度差分定位技术已广泛应用于坝体形变监测、山体滑坡和地面沉降等领域[1]。但在实际应用中,测试数据中会存在较大的数据跳变值,直接对数据稳定性和精度的确定造成影响,不利于对形变监测、山体滑坡和地面沉降分析预测的判断[2]。针对实际数据精度差、稳定度低的问题,本文采用莱依达准则对跳变数据进行修正,并进行正态分布检验,在满足正态分布检验的条件下利用均值和方差的稳定度处理方法,实现高稳定度和高精度的数据处理方法。
1 系统组成
系统组成主要分为2部分:测站和控制中心。系统组成示意图如图1所示。
1.1 测站
测站主要包括监测站和基准站。系统采用多个监测站来监测大坝同节点的形变状况。监测站的主要组成部分是高级精简指令集机器(advanced RISC machines,ARM)。ARM主要由核心板模块、系统扩展底板、接收机板卡及天线组成。具体组成如图2所示。此外,监测站包括网桥,用来完成观测数据到控制中心的传输。
监测系统使用的天线为HX-BS781A天线,支持全球定位系统(global positioning system,GPS) L1/L2频点、北斗卫星导航系统(BeiDou navigation satellite system,BDS) B1/B2/B3和格洛纳斯卫星导航系统(global navigation satellite system,GLONASS) L1/L2频点,低噪放增益为40 dB。接收机板卡为NovAtel公司推出的BDM610 GNSS板卡,支持GPS L1/L2和BDS B1/B2频点,有功耗低、尺寸小的优点。BDM610板卡单点L1水平定位精度为1.5 m,其中GPS L1的码测量精度为10 cm,载波测量精度为0.6 mm,数据的更新频率为1 Hz。
ARM平台搭载Wince 6.0操作系统,通过通信软件,控制核心板模块从底板逻辑门电路(transistor-transistor logic,TTL)接口读取接收机板卡的观测数据,通过网口将数据传输到网桥,进而传输到指定网络协议(internet protocol,IP)的控制中心服务器端。
基准站和监测站的硬件部分一致,不同的是在接收机配置上,基准站需标定准确的位置信息,并配置到接收机板卡中。
1.2 控制中心
控制中心设置在大坝附近,主要由网桥和电脑组成。
电脑通过网桥连接基准站和各个监测点,接收来自各站点的原始观测数据,并将数据通过IP来区分,利用电脑中的实时动态差分(real time kinematic,RTK)软件进行基线求解,并将差分定位的结果输出,作为判断大坝形变的依据。
大坝安全监测系统RTK软件部分主要通过串口读取网口传输的二进制数据流,并根据接收机输出的数据格式将原始的二进制数据保存成数据帧,然后根据数据帧对不同数据段的定义解码得到原始观测数据值,再利用观测值信息做基线解算[3]。高精度差分定位软件流程如图3所示。
模块初始化过程中,根据配置文件来选择GPS、BDS或双系统组合定位。软件读取所要解码的二进制数据,数据来源可以选择实时观测数据,也可以选择历史数据文件读取。读取完成后,根据指令格式定义对数据帧进行解码得到相应观测值,如定位结果、载波相位值、码伪距值等。根据解码出的数据,利用双差数学模型[4]求解出每个历元的整周模糊度浮点解,将浮点解应用最小二乘模糊度去相关平差[5-6](least squares ambiguity decorrelation adjustment method,LAMBDA)算法,求得整周模糊度的固定解,由整周模糊度固定解[7-8]即可求出基准站至流动站的基线矢量。最后,结果输出模块输出星历数据和基线矢量在北向、东向和天向的分量,并由分量判断大坝的偏移状况。
2 高稳定度数据处理方法
2.1 莱依达(PauTa)准则——野值修正方法
在实际监测数据中,一组观测值若混有粗差值而没被剔除,将影响最后预测结果。但是,通常一组正确的观测值是分散的,它客观反映了系统在某种特定条件下的随机波动性。为了得到精度更高的结果,人为丢掉一些误差大的观测值,由此得到高精度数据是不科学的,因此需要正确地取舍观测值。

对观测数据序列{x1,x2,…,xN},描述该序列数据的变化特征为
dj=(xj-xj-1)-(xj+1-xj)
(j=2,3,…,N-1)。
(1)

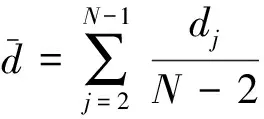
(2)
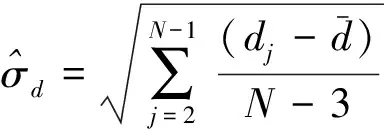
(3)
根据dj偏差的绝对值与均方差的比值为
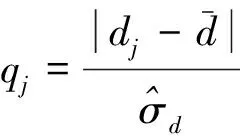
(4)
当qj>3时,则认为xj是奇异值,应予以舍弃。为保持数据序列的连续性,对舍弃的奇异值,用一个与前一点数值相等的数据补上。野值修正的流程如图4所示。
2.2W检验——正态分布检验法
关于总体正态性的检验有一些专门方法,其中常用的有偏度峰度联合检验法、正态概率纸检验法和W检验法。由于偏度峰度联合检验法要求样本容量大,正态概率纸检验法虽然直观且计算较简单,但精度不高;因此主要采用有Shapior和Wilk于提出的W检验法,它灵敏度高、计算简单、需要样本容量小的优点[10]。
W检验法是由样本X1,X2,…,XN的顺序统计量X(1),X(2),…,X(n)构成检验统计量为

(5)

(6)
ak由查表可得。可以证明,对任何分布的样本值(x1,x2,…,xn),W的观测值都满足0≤W<1,而且分布越接近正太分布,W的值越接近1。
W的检验法则为:
若W≤Wα,则拒绝正态性假设,即认为总体不服从正态分布;
若Wα 其中Wα可从查表得到,α为显著性水平,可根据不同情况取α=0.10、α=0.05和α=0.01。 2.3 稳定度确定方法 高精度差分定位结果中需要判断该时间序列中的一段数据是否稳定可用。稳定度较高的数据均值和方差波动较小,稳定度低的数据均值和方差波动较大[11]。因此,本文从均值和方差的角度计算出序列的稳定度。 2.3.1 均值变化法 设差分定位的采样时间间隔为t,将差分定位结果x方向时间序列(x1,x2,x3,…)按长度为k(k个观测历元)的搜索窗口将其实时分段成{(x1,…,xk),(xk+1,…,x2k),(x2k+1,…,x3k),…},按式(7)求出各段的均值并组成均值序列(avg1,avg2,avg3,…)。并可认为,当x坐标处于非平稳状态时,其均值序列相邻均值大小变化较大;处于平稳状态时,相邻均值变化较小。均值为 (7) 为了具体说明,定义阈值d,当满足稳定条件,即式(8)时,可以认为该相邻均值所对应的x坐标段已达到平稳,其收敛点认为是这2个均值所对应的x坐标段中观测历元最小的点,稳定条件为 (8) (9) 均值变化法的流程如图5所示。 2.3.2 方差变化法 方差变化法和均值变化法类似,只不过是从方差变化情况来判断时间序列是否平稳;与均值变化法不同的地方如下: 方差为var=E[∑(x-avg)2]; (10) (11) 实际测试地点位于福建省泉州山美水库,基准站设置在控制中心楼顶,通过长时间测绘得到基准站的准确坐标:25.162 707 11°N,118.414 165 5°E,128.809 617 6m(H方向),配置到基准站接收机中。实际测试场景如图6所示。 在山美水库大坝,实际测得长基线(约260 m)数据,测试时间大约277 min,其中利用GPS L1频点测得的基线矢量以及北向、东向和高程方向的分量结果如图7所示。 由图7可得出,基线长度在260.255 m上下波动,北向分量在-118.645 m上下波动,东向分量在-230.400 m上下波动,而高程分量在-23.885 m上下波动。 3.1 野值修正 图7中除了正常的波动情况外,在第131、134和第476 s左右,基线有较大的波动值;在同样的历元条件下,北向、东向和天向分量也分别有一个变化较大的值。这个值的产生,可能是多径或其他外在因素造成的,也可能是换星过程中产生的,这些值称为奇异值(或野值)。 利用莱依达准则,对原始数据进行野值的修正。考虑到数据的连续性,将检验出的野值修正为上一组数据的均值。将16 677 s原始数据的标准差作为经验值σ,如表1所示。经野值修正后,得到的各方向分布结果如图8所示。 由图8可知,在野值修正前后,图中数据偏差较大的野值点已不存在。这有利于后期对实测数据的稳定性及精度分析,避免了野值对系统稳定性和精度的影响,同时减少了系统的误警率。表1为野值修正前后标准差对比。 表1 野值修正前后标准差对比 m 从表中可以看出:去野值前,基线存在较大的野值点,因此统计的基线和各分量的标准差较大;野值修正后,基线的标准差变约为原来的1/4,北向和天向分量约为原始数据的1/2,而东向分量为原来的1/10。说明野值修正后,数据分布更加集中。 3.2 正态分布检验 利用W检验法对基线矢量的分布进行检验。为了严格检验数据的正态分布特性,显著性水平取较小值,即α=0.01,查表得Wα=0.930。在数据源中,随机选取其中的50组数据,经W检验,得到基线的检验值WBaseline=0.981 4,而Wα=0.930 0,故Wα 表2 各方向分量W检验结果 北向、东向和天向的频率和概率密度分布如图9所示。由正频率分布和概率密度分布曲线可知,东向分量的分布正态性最强,其W检验的结果值也最接近与1,远大于Wα,服从正态分布。同理,天向分量的分布结果正态性较差,且其检验结果较接近于Wα,偏离1较多,但其检验值仍大于Wα;故天向分量也服从正态分布。综上,北向、东向和天向的分布均服从正态分布。 3.3 稳定度确定方法 在数据稳定度确定过程中,结合大坝应用的实际精度需求:北向、东向精度为5mm,垂直精度8mm;因此将北、东、天3个方向分量的阈值分别设置为5、5和8mm。 大坝监测过程中,每5min输出一次结果。为了更详尽地分析数据的稳定性及可用性,在此实验中,选取1min作为时间单元来输出解算结果,即采样时间间隔t=60 s。 3.3.1 均值变化法 图10为均值变化对结果的分析处理。 图10中的虚线代表大坝监测所需达到的精度(北向、东向分量5mm,天向分量8mm),实线代表实测数据的均值精度。经统计得到,利用均值变化法,北向精度达到要求的比例为99.28 %,东向为100 %,天向为96.03 %。其中,东向分量的满足精度要求的比例最高,北向分量次之,天向分量最低。结果如表3所示。 表3 均值变化法稳定度结果 (%) 3.3.2 方差变化法 方差变化法的稳定度检验分布如图11所示。图11中虚线代表大坝各方向分量所需达到的精度,实线代表实测的各方向分量的标准差精度。具体满足精度的结果如表4所示。 表4 方差变化法稳定度分析 (%) 从图11和表4中可知:北向和东向分量的标准差小于0.005 m,天向分量的标准差小于0.008 m;而且,北向和天向分量达到精度要求的比例均为100 %,天向分量达到精度要求的比例为96.03 %。 基准站和监测站之间的基线矢量是东西方向的,因而在东向上消除的误差最多;故其精度最高。高程方向满足精度要求的比例最低,一方面因为用来解算的卫星仰角都较高,位于天线上方,因此高程方向本身定位精度误差较大;另一方面,矢量在高程方向的分量仅为23 m左右,明显小于北向(118 m)和东向(230 m)分量,故差分在天向消除的误差最小。综上所述,北向、东向和天向分量精度均满足大坝形变监测要求,且北向和东向分量稳定度高于99 %,天向分量高于96 %。 本文将GNSS高精度差分定位应用于大坝形变监测中,重点针对大坝监测高精度和高稳定度的需求,对数据进行了野值剔除、正态分布检验和稳定性检验,通过实际数据验证了系统监测结果符合大坝要求。 文中提出的野值检验及修正方法,可以针对实际测试过程中出现的跳变野值进行过滤,减少野值对大坝监测精度造成的影响。利用W检验法对大坝实测数据进行检验,验证了基线矢量的北向、东向和天向分量均服从正态分布,并利用均值变化法和方差变化法对各方向的分量进行了稳定度确定,同时计算出其均值精度和方差精度,北向和东向分量的精度达标率均高于99 %,天向分量高于96 %,满足大坝形变监测的需求,证明了高稳定度数据处理方法的可行性和有效性,可为GNSS高精度差分定位应用的推广提供参考。 [1] KAPLAN E D.GPS原理与应用[M].寇艳红,译.2版.北京:电子工业出版社,2012:476-494. [2] 伊晓东,李保平.变形监测技术及应用[M].郑州:黄河水利出版社,2007:4-5. [3] 陈万通,金天.一种基于GPS的单频单历元姿态解算算法[J].航空科学技术,2010,27(1):25-29. [4] YANG C C.GPS phase double difference method for single axis attitude determination[D].Taipei:National Taiwan University,1994. [5] VERHAGEN S,TEUNISSEN P J G.New global navigation satellite system ambiguity resolution method compared to existing approaches[J].Guidance,Control & Dynamics,2006,41(3):89-103. [6] TEUNISSEN P J G.The LAMBDA method for the GNSS compass[J].Artificial Satellites,2006,41(3):89-103. [7] BUIST P J.The baseline constrained LAMBDA method for single epoch,single frequency attitude determination applications[C]//The Institute of Navigation.Proceedings of the 21st International Technical Meeting of The Satellite Division of the Institute of Navigation(ION GNSS 2008).Fort Worth,TX:The Institute of Navigation,Inc.2008:2962-2973. [8] MISRA P,ENGE P.Global positioning system:signals,measurements,and performance[M].2nd ed.Lincoln MA:Ganga-Jamuna Press,2006. [9] 黄声亨,尹军,蒋征,等.变形监测数据处理 [M].2版.武汉:武汉大学出版社,2010:69-70. [10]胡细宝,孙洪祥,王丽霞.概率论、数理统计与随机过程[M].北京:北京邮电大学出版社,2011:301-303. [11]周承松,彭月,张小红,等.精密单点定位收敛时间的确定方法研究[J].导航定位学报,2016,4(1):80-87. Application of differential data processing technology in deformation monitoring WANGDongdong,HUANGZhigang,QINHonglei,LIANGXiao (School of Electronic and Information Engineering,Beihang University,Beijing 100191,China) Aiming at the problem that there is data jump,low stability and low precision of positioning in the practical application of GNSS high-precise differential technology,the paper proposed a processing method of differential data with high-precision and high-stability by using means of outliers inspection and correction,normal distribution test and high-stability data analysis.Result proved the feasibility of the proposed method,which could provide a reference for the application of GNSS high-precise differential positioning. data processing;deformation monitoring;GNSS;high-stability;high-precision 2016-06-21 王东东(1992—),男,河北保定人,硕士生,研究方向为卫星导航和高精度差分定位。 王东东,黄智刚,秦红磊,等.差分数据处理技术在形变监测中的应用[J].导航定位学报,2017,5(1):108-114.(WANG Dongdong,HUANG Zhigang,QIN Honglei,et al.Application of differential data processing technology in deformation monitoring[J].Journal of Navigation and Positioning,2017,5(1):108-114.) 10.16547/j.cnki.10-1096.20170123. P228 A 2095-4999(2017)01-0108-07
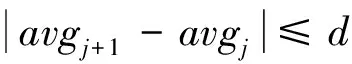

3 实验与结果分析




4 结束语

