棒棒糖图的奇优美性和奇强协调性
童细心,林育青
(汕头职业技术学院自然科学系,广东汕头515041)
棒棒糖图的奇优美性和奇强协调性
童细心,林育青
(汕头职业技术学院自然科学系,广东汕头515041)
研究了棒棒糖图Cn+Pl的奇优美性和奇强协调性,得到了棒棒糖图Cn+Pl在n=4k,4k+2时是奇优美图,在n=4k时是奇强协调图等结论.
棒棒糖图;奇优美标号;奇优美图;奇强协调标号;奇强协调图.
0 引言
优美图是图论中一个十分有趣且重要的内容,对优美图的研究始于1967年,由于其标号问题的应用十分广泛,一直是人们研究的热点.1991年,Gnanajoethi提出一个猜想:“每棵树都是奇优美的”[1];1982年,Fank Hsu D[2]引入了图的强协调标号,从而使图的标号研究更加丰富,目前已取得了很多研究成果[1-11].由于缺乏一个系统和有力的工具,迄今只能对一些特殊图类探索其奇优美性和奇强协调性.
定义1[1]:对于简单图G=(V,E),若∀v∈V,存在单射(f(v)称为顶点v的标号),且导出的边标号满足g是E到的一个一一对应,则称图G是奇优美图,称f为图G的奇优美标号.
定义2[2]:对于简单图G=(V,E),若∀v∈V,存在单射,且导出的边标号g(e)=g(uv)=f(u)+f(v)满足g是E到的一个一一对应,则称图G是奇强协调图,称f为图G的奇强协调标号.
定义3[12]:从圈Cn上的一个顶点ui悬挂一条长为l的路Pl所得到的图类,称为棒棒糖图,记为Cn+Pl.如图1所示,我们记圈Cn的顶点为ui,i=1,2,…,n.路Pl的顶点为vi,i=1,2,…,l.

图1 棒棒糖图Cn+Pl
本文研究了棒棒糖图Cn+Pl的奇优美性及其奇强协调性,得到了如下结果:
定理1:当n=4k时,棒棒糖图Cn+Pl是奇优美图.
定理2:当n=4k+2时,棒棒糖图Cn+Pl是奇优美图.
定理3:当n=4k时,棒棒糖图Cn+Pl是奇强协调图.
本文中所讨论的图均为无向简单图,v表示顶点v,uv表示以u,v为顶点的边,f(v)表示点v的标号,简记为v=f(v);同理,f(uv)表示边uv的标号,也简记为uv=f(uv).其他未加说明的定义和符号均来自文[13].
1 定理1的证明
我们分n=4k,l=2t-1和n=4k,l=2t两种情况证明棒棒糖图是奇优美图.
1.1 情形1
当n=4k,l=2t-1时,棒棒糖图Cn+Pl是奇优美图.
当n=4k,l=2t-1时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t-1,边数为n+l=4k+2t-1,此时.给出棒棒糖图Cn+Pl的各顶点的标号递推算法A如下:
(1)v2i-1=2i-2,i=1,2,…,t;
(2)v2i=8k+4t-2i-1,i=1,2,…,t-1;
(3)u2i-1=8k+2t-2i+1,i=1,2,…,2k;
(4)u2i=2t+2i-2,i=1,2,…,k;u2i=2t+2i,i=k+1,k+2,…,2k.
按照算法A可得以下结果:
引理1:当n=4k,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t-3}构成单射.
证明:当n=4k,l=2t-1时,记M是棒棒糖图Cn+Pl的所有顶点标号集合,由算法A的(1)-(4)易知:

由此易验证,Mi∩Mj=φ,i≠j且i,j=1,2,3,4.即当n=4k,l=2t-1时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合M=M1∪M2∪M3∪M4中最小数是0(在M1中),最大数是8k+4t-3(在M2中),即当n=4k,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t-3}构成单射.
引理2:当n=4k,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t-3}构成一一对应.
证明:由算法A知,各顶点的标号最小为零,最大为8k+4t-3,故边的标号均不超过8k+4t-3.我们把边的标号分为两大类来考虑.
(一)由算法A的(1)(2)(3)可知路v1v2…vlu1中边的标号有以下几种情况:

(二)由算A法的(3)(4)可知圈u1u2…u4ku1中边的标号有以下几种情况:
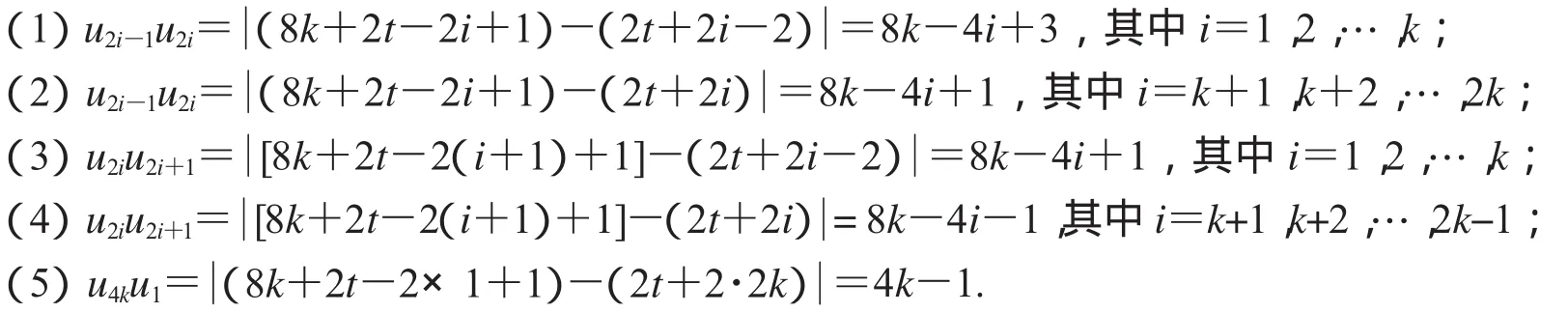
首先,由(一)易知,在路v1v2…vlu1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)8k+5≤v2i-1v2i≤8k+4t-3,其中i=1,2,…,t-1;
(2)8k+3≤v2iv2i+1≤8k+4t-5,其中i=1,2,…,t-1;
(3)v2t-1u1=8k+1.
由边的标号范围及等差数列的性质知,在路v1v2…vlu1中各边的标号不相等.
其次,由(二)易知,在圈u1u2…u4ku1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)4k+3≤u2i-1u2i≤8k-1,其中i=1,2,…,k;
(2)1≤u2i-1u2i≤4k-3,其中i=k+1,k+2,…,2k;
(3)4k+1≤u2iu2i+1≤8k-3,其中i=1,2,…,k;
(4)3≤u2iu2i+1≤4k-5,其中i=k+1,k+2,…,2k-1;
(5)u4ku1=4k-1.
由边的标号范围及等差数列的性质知,在圈u1u2…u4ku1中各边的标号不相等.
最后,由上易知,两类边的标号范围互不重叠,故也互不相等.
综上所述,当n=4k,l=2t-1时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t-3}构成一一对应.
由引理1、引理2及定义1知,情形1成立,即当n=4k,l=2t-1时,棒棒糖图Cn+Pl是奇优美图.
1.2 情形2
当n=4k,l=2t时,棒棒糖图Cn+Pl是奇优美图.
当n=4k,l=2t时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t,边数为n+l=4k+2t,此时.给出棒棒糖图Cn+Pl的各顶点的标号递推算法B如下:
(1)v2i-1=2i-2,i=1,2,…,t;
(2)v2i=8k+4t-2i+1,i=1,2,…,t;
(3)u2i-1=2t+2i-2,i=1,2,…,2k;
(4)u2i=8k+2t-2i+1,i=1,2,…,k;u2i=8k+2t-2i-1,i=k+1,k+2,…,2k.
按照算法B可得以下结果:
引理3:当n=4k,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t-1}构成单射.
证明:当n=4k,l=2t时,记N是棒棒糖图Cn+Pl的所有顶点标号集合,由算法B的(1)-(4)易知:

由此易验证,Ni∩Nj=φ,i≠j且i,j=1,2,3,4.即当n=4k,l=2t时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合N=N1∪N2∪N3∪N4中最小数是0(在N1中),最大数是8k+4t-1(在N2中).即当n=4k,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t-1}构成单射.
引理4:当n=4k,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t}构成一一对应.
证明:由算法B知,各顶点的标号最小为零,最大为8k+4t-1,故边的标号均不超过8k+4t-1.我们把边的标号分为两大类来考虑.
(一)由算法B的(1)(2)(3)可知路v1v2…vlu1中边的标号有以下几种情况:

(二)由算法B的(3)(4)可知圈u1u2…u4ku1中边的标号有以下几种情况:

首先,由(一)易知,在路v1v2…vlu1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)8k+3≤v2i-1v2i≤8k+4t-1,其中i=1,2,…,t;
(2)8k+5≤v2iv2i+1≤8k+4t-3,其中i=1,2,…,t-1;
(3)v2tu1=8k+1.
由边的标号范围及等差数列的性质知,在路v1v2…vlu1中各边的标号不相等.
其次,由(二)易知,在圈u1u2…u4ku1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)4k+3≤u2i-1u2i≤8k-1,其中i=1,2,…,k;
(2)1≤u2i-1u2i≤4k-3,其中i=k+1,k+2,…,2k;
(3)4k+1≤u2iu2i+1≤8k-3,其中i=1,2,…,k;
(4)3≤u2iu2i+1≤4k-5,其中i=k+1,k+2,…,2k-1;
(5)u4ku1=4k-1.
由边的标号范围及等差数列的性质知,在圈u1u2…u4ku1中各边的标号不相等.
最后,由上易知,两类边的标号范围互不重叠,故也互不相等.
综上所述,当n=4k,l=2t时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t-1}构成一一对应.
由引理3、引理4及定义1知,情形2成立,即当n=4k,l=2t时,棒棒糖图Cn+Pl是奇优美图.
定理1:当n=4k时,棒棒糖图Cn+Pl是奇优美图.
证明:由情形1、情形2可知,定理1成立.
2 定理2的证明
同样分n=4k+2,l=2t-1和n=4k+2,l=2t两种情况证明棒棒糖图是奇优美图.
2.1 情形3
当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl是奇优美图.
当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t+1,边数为n+l=4k+2t+1,此时.给出棒棒糖图Cn+Pl的各顶点的标号递推算法C如下:
(1)v2i-1=2i-2,i=1,2,…,t;
(2)v2i=8k+4t-2i+3,i=1,2,…,t-1;
(3)u2i-1=8k+2t-2i+5,i=1,2,…,k+1;u2i-1=8k+2t-2i+3,i=k+2,k+3,…,2k+1;
(4)u2i=2t+2i-2,i=1,2,…,2k;u4k+2=4k+2t+2.
按照算法C可得以下结果:
引理5:当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t+1}构成单射.
证明当n=4k+2,l=2t-1时,记P是棒棒糖图Cn+Pl的所有顶点标号集合,由算法C的(1)-(4)易知:

由此易验证,Pi∩Pj=φ,i≠j且i,j=1,2,3,4.即当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合P=P1∪P2∪P3∪P4中最小数是0(在P1中),最大数是8k+4t+1(在P2中),即当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t+1}构成单射.
引理6:当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t+1}构成一一对应.
证明:由算法C知,各顶点的标号最小为零,最大为8k+4t+1,故边的标号均不超过8k+4t+1.我们可把边的标号分为两大类来考虑.
(一)由算法C的(1)(2)(3)可知路v1v2…vlu1中边的标号有以下几种情况:

(二)由算法C的(3)(4)可知圈u1u2…u4k+2u1中边的标号有以下几种情况:

首先,由(一)易知,在路v1v2…vlu1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)8k+9≤v2i-1v2i≤8k+4t+1,其中i=1,2,…,t-1;
(2)8k+7≤v2iv2i+1≤8k+4t-1,其中i=1,2,…,t-1;
(3)v2t-1u1=8k+5.
由边的标号范围及等差数列的性质知,在路v1v2…vlu1中各边的标号不相等.
其次,由(二)易知,在圈u1u2…u4k+2u1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)4k+3≤u2i-1u2i≤8k+3,其中i=1,2,…,k+1;
(2)5≤u2i-1u2i≤4k-3,其中i=k+2,k+3,…,2k;
(3)u4k+1u4k+2=1;
(4)4k+5≤u2iu2i+1≤8k+1,其中i=1,2,…,k;
(5)3≤u2iu2i+1≤4k-1,其中i=k+1,k+2,…,2k;
(6)u4k+2u1=4k+1.
由边的标号范围及等差数列的性质知,在圈u1u2…u4k+2u1中各边的标号不相等.
最后,由上易知,两类边的标号范围互不重叠,故也互不相等.
综上所述,当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t+1}构成一一对应.
由引理5、引理6及定义1知,情形3成立,即当n=4k+2,l=2t-1时,棒棒糖图Cn+Pl是奇优美图.
2.2 情形4
当n=4k+2,l=2t时,棒棒糖图Cn+Pl是奇优美图.
当n=4k+2,l=2t时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t+2,边数为n+l=4k+2t+2,此时.此时给出棒棒糖图Cn+Pl的各顶点的标号递推算法D如下:
(1)v2i-1=2i-2,i=1,2,…,t;
(2)v2i=8k+4t-2i+5,i=1,2,…,t;
(3)u2i-1=2t+2i-2,i=1,2,…,k+1;u2i-1=2t+2i,i=k+2,k+3,…,2k+1;
(4)u2i=8k+2t-2i+5,i=1,2,…,2k;u4k+2=4k+2t+1.
按照算法D可得以下结果:
引理7:当n=4k+2,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t+3}构成单射.
证明:当n=4k+2,l=2t时,记Q是棒棒糖图Cn+Pl的所有顶点标号集合,由算法D的(1)-(4)易知:

易验证,Qi∩Qj=φ,i≠j且i,j=1,2,3,4.即当n=4k+2,l=2t时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合Q=Q1∪Q2∪Q3∪Q4中最小数是0(在Q1中),最大数是8k+4t+3(在Q2中),即当n=4k+2,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+4t+3}构成单射.
引理8:当n=4k+2,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t+3}构成一一对应.
证明:由算法D知,各顶点的标号最小为零,最大为8k+4t+3,故边的标号均不超过8k+4t+3.我们可把边的标号分为两大类来考虑.
(一)由算法D的(1)(2)(3)可知路v1v2…vlu1中边的标号有以下几种情况:

(二)由算法C的(3)(4)可知圈u1u2…u4k+2u1中边的标号有以下几种情况:


首先,由(一)易知,在路v1v2…vlu1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)8k+7≤v2i-1v2i≤8k+4t+3,其中i=1,2,…,t;
(2)8k+9≤v2iv2i+1≤8k+4t+1,其中i=1,2,…,t-1;
(3)v2tu1=8k+5.
由边的标号范围及等差数列的性质知,在路v1v2…vlu1中各边的标号不相等.
其次,由(二)易知,在圈u1u2…u4k+2u1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)4k+3≤u2i-1u2i≤8k+3,其中i=1,2,…,k+1;
(2)5≤u2i-1u2i≤4k-3,其中i=k+2,k+3,…,2k;
(3)u4k+1u4k+2=1;
(4)4k+5≤u2iu2i+1≤8k+1,其中i=1,2,…,k;
(5)3≤u2iu2i+1≤4k-1,其中i=k+1,k+2,…,2k;
(6)u4k+2u1=4k+1.
由边的标号范围及等差数列的性质知,在圈u1u2…u4k+2u1中各边的标号不相等.
最后,由上易知,两类边的标号范围互不重叠,故也互不相等.
综上所述,当n=4k+2,l=2t时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k+2,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+4t+3}构成一一对应.
由引理7、引理8及定义1知,情形4成立,即当n=4k+2,l=2t时,棒棒糖图Cn+Pl是奇优美图.
定理2:当n=4k+2时,棒棒糖图Cn+Pl是奇优美图.
证明:由情形3、情形4可知,定理2成立.
3 定理3的证明
当n=4k时,棒棒糖图Cn+Pl的顶点数为n+l=4k+l,边数为n+l=4k+l,此时.给出棒棒糖图Cn+Pl的各顶点的标号递推算法E如下:
(1)vi=i-1,i=1,2,…,l;
(2)u2i-1=l+2i-2,i=1,2,…,2k;
(3)u2i=l+2i-1,i=1,2,…,k;u2i=l+2i+1,i=k+1,k+2,…,2k.
按照算法E可得以下结果:
引理9:当n=4k时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+2l-1}构成单射.
证明:当n=4k时,记R是棒棒糖图Cn+Pl的顶点标号集合,由算法E的(1)-(3)易知:


易验证,Ri∩Rj=φ,i≠j且i,j=1,2,3.即当n=4k时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合R=R1∪R2∪R3中最小数是0(在R1中),最大数是l+4k+1(在R3中,且显然小于8k+2l-1).所以,当n=4k时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,8k+2l-1}构成单射.
引理10:当n=4k时,棒棒糖图Cn+Pl的边集与集合{1,3,5,…,8k+2l-1}构成一一对应.
证明:由算法E知,我们把边的标号分为两大类来考虑.
(一)由算法E的(1)(2)可知路v1v2…vlu1中边的标号有以下几种情况:
(1)vivi+1=(i+l)+[(i+1)-1]=2i-1,其中i=1,2,…,l-1;
(2)vlu1=(l-1)+(l+2×1-2)=2l-1.
(二)由算法E的(2)(3)可知圈u1u2…u4ku1中边的标号有以下几种情况:
(1)u2i-1u2i=(l+2i-2)+(l+2i-1)=2l+4i-3,其中i=1,2,…,k;
(2)u2i-1u2i=(l+2i-2)+(l+2i+1)=2l+4i-1,其中i=k+1,k+2,…,2k;
(3)u2iu2i+1=(l+2i-1)+[l+2(i+1)-2]=2l+4i-1,其中i=1,2,…,k;
(4)u2iu2i+1=(l+2i+1)+[l+2(i+1)-2]=2l+4i+1,其中i=k+1,k+2,…,2k-1;
(5)u4ku1=(l+2·2k+1)+(l+2×1-2)=2l+4k+1.
首先,由(一)易知,在路v1v2…vlu1中,各边的标号均为奇数,且范围为:
其次,由(二)易知,圈u1u2…u4ku1中,各边的标号均为奇数,都是以4为公差的等差数列,且范围为:
(1)2l+1≤u2i-1u2i≤2l+4k-3,其中i=1,2,…,k;
(2)2l+4k+3≤u2i-1u2i≤2l+8k-1,其中i=k+1,k+2,…,2k;
(3)2l+3≤u2iu2i+1≤2l+4k-1,其中i=1,2,…,k;
(4)2l+4k+5≤u2iu2i+1≤2l+8k-3,其中i=k+1,k+2,…,2k-1;
(5)u4ku1=2l+4k+1.
由边的标号范围及等差数列的性质知,在圈u1u2…u4ku1中,各边的标号不相等.
最后,由上易知,两类边的标号范围互不重叠,故也互不相等.
综上所述,当n=4k时,棒棒糖图Cn+Pl各边的标号均不相同,且全为奇数.即当n=4k时,棒棒糖图Cn+Pl边集与集合{1,3,5,…,8k+2l-1}构成一一对应.
定理3:当n=4k时,棒棒糖图Cn+Pl是奇强协调图.
证明:由引理9、引理10及定义2知,定理3成立.
[1]GNANAJOETHI R B.Topics is graph theory[D].India:Madurai Kamaraj University,1991.
[2]HSU D F.Harmonious labelings of windmill graphs and related graphs[J].Journal of Graph Theory.1982,6(1):85-87.
[3]RINGEL G.Problem 25,theory of graphs and its application[J].Proc Symposium Smolenice,1963:162-167.
[4]GALLIAN J A.A dynamic survey of graph labeling[J].The Electronic Journal of Combinatorics,2009,16(6):1-219.
[5]林育青,钟发胜,童细心,等.图P3n的奇优美标号算法[J].数学理论与应用,2013,33(4):29-34.
[6]林育青,张玲瑛,钟发胜,等.关于奇优美图及奇强协调图的一点注记[J].贵州师范大学学报(自然科学版),2014,32(2):43-46.
[7]童细心,林育青,钟发胜.圈Cn的奇优美性和奇强协调性[J].西南师范大学学报(自然科学版),2014,39(8):10-13.
[8]童细心.一类哑铃图的优美性和奇强协调性[J].汕头大学学报(自然科学版),2015,30(2):38-43.
[9]童细心.哑铃图2Cn+Pl的奇优美性和奇强协调性[J].海南师范大学学报(自然科学版),2015,28(1):15-19.
[10]童细心.一类哑铃图的奇优美性和奇强协调性[J].贵州师范大学学报(自然科学版),2015,33(3):54-58.
[11]林育青,童细心,张玲瑛.太阳图的奇优美性和奇强协调性[J].数学的实践与认识,2015,45(18):271-280.
[12]陈暑波,夏方礼,龙韬,等.棒棒糖图的Merrifield-Simmons和Hosoya指数[J].湖南城市学院学报(自然科学版),2008,17(3):39-41.
[13]BANDY J A,MURTY U S R.Graph theory with application[M].NewYork:American Elsevier Publishing Co Inc,1976.
Odd Gracefulness and Odd Strong Harmoniousness of Lollipop Graphs
TONG Xixin,LIN Yuqing
(Department of Natural Sciences,Shantou Polytechnic,Shantou 515041,Guangdong,China)
Odd gracefulness and odd strong harmoniousness of lollipop graphs Cn+Plhave been studied.It is shown that lollipop graphs Cn+Plare odd graceful graph when n=4k,4k+2,and that lollipop graphs Cn+Plare odd strongly harmonious graph when n=4k.
lollipop graphs;odd graceful labeling;odd graceful graph;odd strongly harmonious labeling;odd strongly harmonious graph.
O157.5
A
1001-4217(2017)02-0043-10
2016-01-05
童细心(1979—),男(汉族),湖南岳阳人,讲师.研究方向:图论.邮箱:txx2486@126.com.
汕头职业技术学院2014年院级科研课题(SZK2014Y24).

