修正LIU估计下数据删除模型的强影响分析

朱宁，刘庆华

（桂林电子科技大学数学与计算科学学院，广西桂林541004）

修正LIU估计下数据删除模型的强影响分析

朱宁，刘庆华

（桂林电子科技大学数学与计算科学学院，广西桂林541004）

在修正LIU估计下对单个数据删除模型进行研究，讨论数据删除模型估计量的性质，得到修正LIU估计MLE（i）与LIU估计LE间的关系，以及预测估计i可由MLE与yi线性表出等性质；同时，本文在前人的基础上推导得到CRi统计量和Cook统计量新的表达形式，并在实例中用Cook距离来识别强影响点，验证其合理性.

修正LIU估计；数据删除模型；Cook统计量；强影响点

0 引言

考虑一般的线性模型：

其中y为n×1阶观测，X为n×p阶列满秩设计阵，β为p×1阶未知参数向量，ε为n×1随机误差向量，I为n阶单位矩阵.在线性模型的参数估计理论和方法中，最小二乘法有很重要的位置.但随着研究的深入，统计学家发现当设计矩阵X'X出现多重共线性或近似的多重共线性时，最小二乘估计（LSE）不再是良好的估计[1].为了解决这一问题，学者提出了一系列有偏估计来改进最小二乘估计.常用的有偏估计包括岭估计[1-4]和主成分估计[1，5]，除了这两种估计之外，另外一类常用的有偏估计是Liu[6]基于Stein提出的Stein估计和岭估计上提出的LIU估计.目前很多学者对LIU估计的性质进行研究，例如文献[7]提出了新的加权混合LIU估计，并在均方误差矩阵准则下研究该估计的优良性，文献[8]对线性约束下的线性回归模型进行约束LIU型估计，并证明该估计在均方误差下比最小二乘估计好等.基于前人基础上，Swindel[9]提出了一种修正的岭估计MRE（k，b0）=（X'X＋kI）-1（X'y＋kb0），Yalian Li和Hu Yang[10]考虑先验信息，通过类似的思想将LIU估计进行修正，得到一种修正的LIU估计.

本文在Yalian Li和Hu Yang[10]所提出的一种修正LIU估计的基础上，结合数据删除模型的特点，对修正LIU估计下的数据删除模型的强影响问题进行研究，推广至有偏估计的数据删除模型的强影响分析，证明修正LIU估计的相关性质，并在前人的基础上提出CRi统计量和Cook统计量新的表达形式，并用该统计量来判断强影响点.

1 修正LIU估计的相关性质

Liu[6]基于Stein提出的Stein估计和岭估计上提出了LIU估计，记为

Yalian Li和Hu Yang[10]在模型（1）下提出了未知参数β的修正LIU估计（MLE），即在LIU估计的基础上对其进行修正，记为：

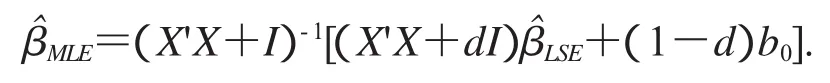
我们将在下文中讨论数据删除模型与修正LIU估计统计量之间的关系.

其中y（i）为（n－1）×1阶观测，X（i）为（n－1）×p阶列满秩设计阵，β（i）为p×1阶未知参数向量，ε（i）为（n－1）×1随机误差向量，I为（n－1）阶单位矩阵.

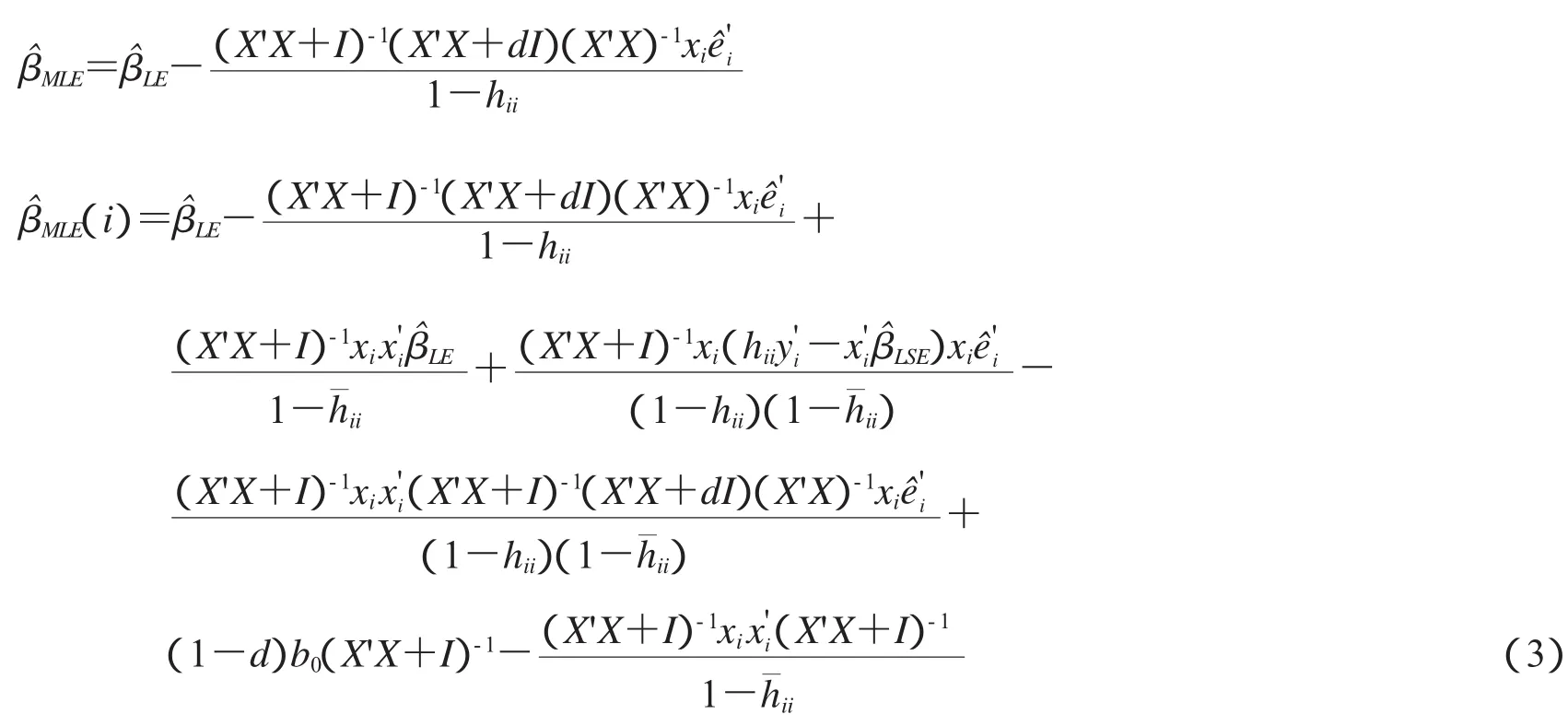
证明：模型（1）中修正LIU估计为

可得到模型（2）中的修正LIU估计：

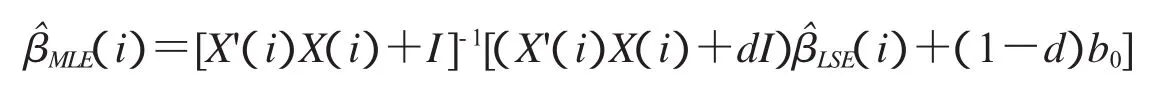
[13]知，模型（2）的LIU估计有如下关系：

再根据和式求逆公式知

结合（4）（5）（6）式可得如下关系

证毕.

证明：

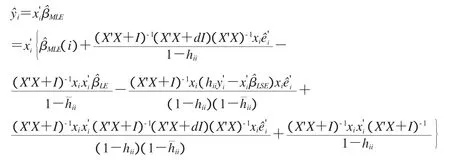
下面引入诊断统计量对强影响点的影响大小进行刻画，并利用统计量识别强影响点.

2 诊断统计量

2.1 协方差比统计量

引理1[1]设A为m×n阵，X为n×1随机向量，Y=AX，则

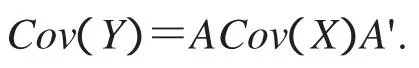
定理2在修正的LIU估计下，协方差比统计量：

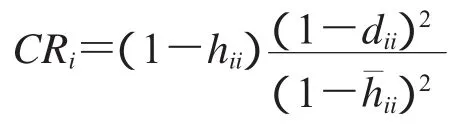
因为

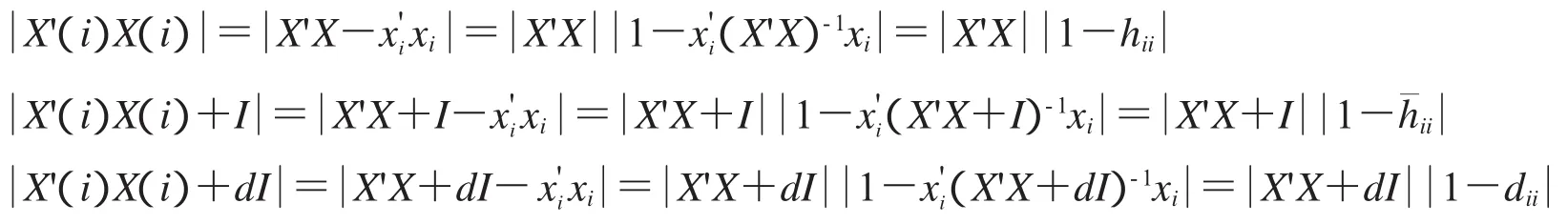
结合引理1，可得到

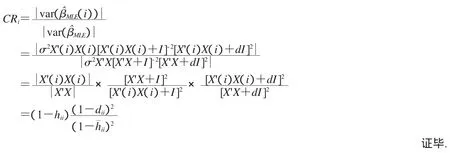
证明：根据文献[12]中模型y（i）=X（i）β（i）＋ε（i）中β和σ2的最小二乘估计与模型（1）中的相对应的和2有如下关系：

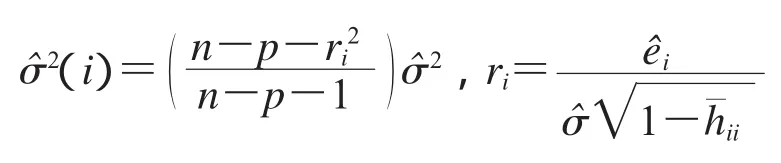
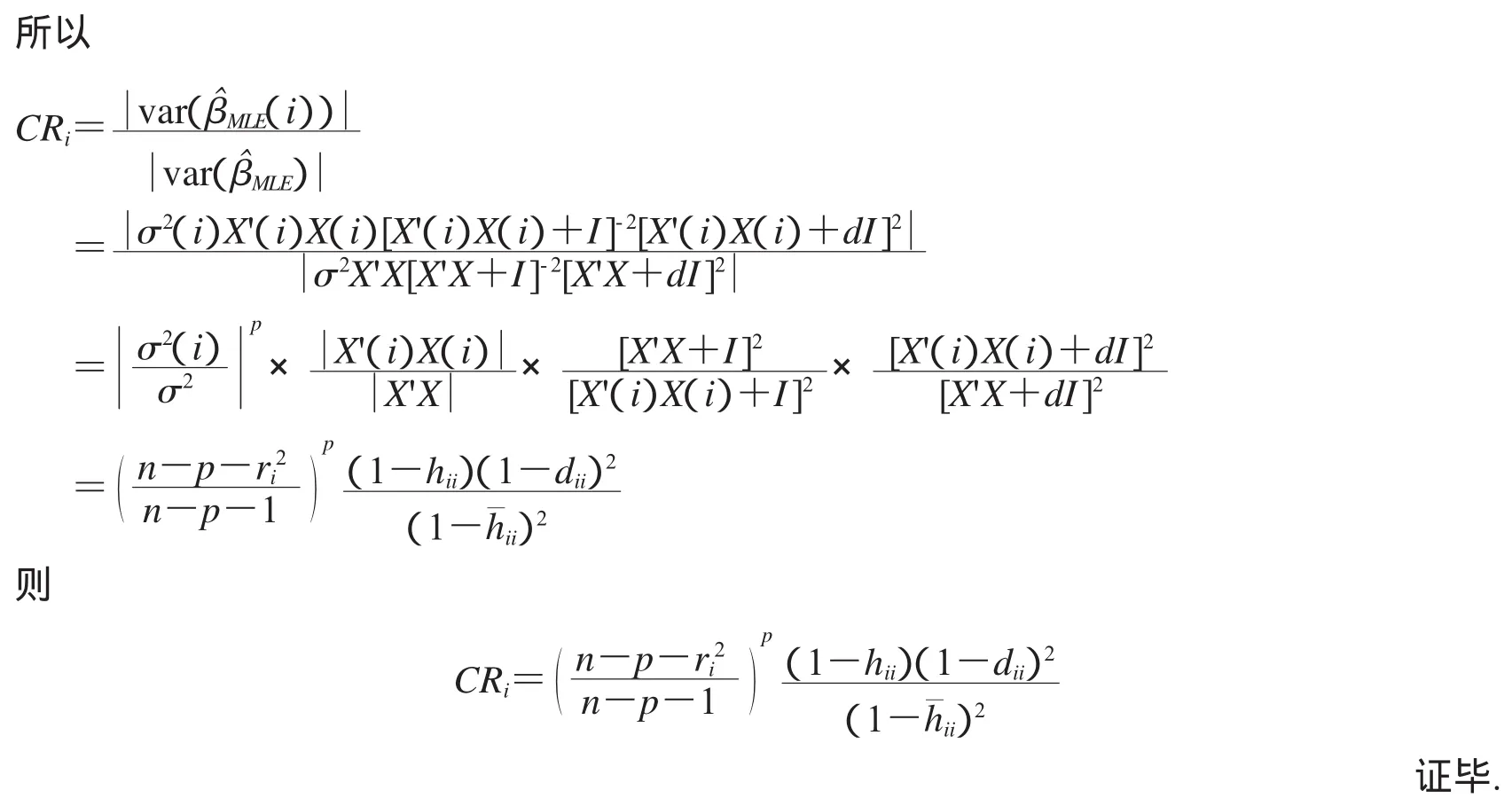
2.2 Cook统计量

定理3在修正LIU估计下，令M=（X'X＋I），c=σ2，Cook统计量可表示成：

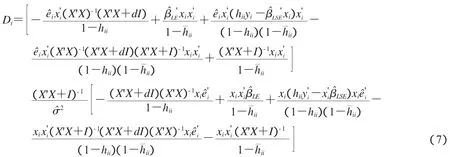
证明：文献[12]中为了度量不同模型对LIU估计的影响程度，定义Cook统计量为：

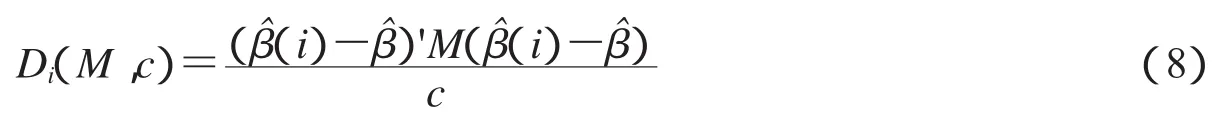
利用（9）式代入（8）式并取M=（X'X＋I），c=σ2，通过整理可推导出（7）式.

证毕.

3 实证分析

案例数据来自文献[1]中例4.2.1煤净化问题，这组数据存在较为严重的共线性.为此我们通过修正LIU估计统计量来估计未知参数是必要的.在此，我们主要研究数据删除模型拟合的好坏程度，并找出强影响点.通过计算得到的影响度量统计量结果见图1和表1.

根据文献[10]本文取b0=0.95LSE，下面分别取不同的d值计算Cook距离，并通过Cook距离来找出强影响点.

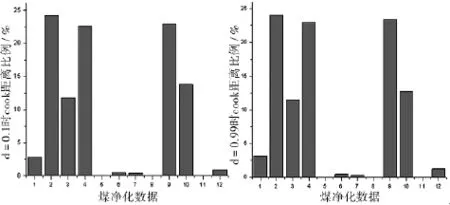
图1 d=0.1or0.99时煤净化数据的Cook距离比例图

表1 d=0.05or0.01当时煤净化数据的Cook距离

当Cook距离Di越大，则说明数据的影响越大.从图1与表1中可以看出，不论取第d=0.05，d=0.01，d=0.1，d=0.99，第2，4，9号数据的Di较大，因此可认为第2，4，9号数据点是强影响点.我们还可以从上表及图中各影响点对整体影响程度进行分析，第2，4，9号数据点Di所占的比例均为23%左右，可见这三个影响点对整体数据影响相当.

4 小结

在修正LIU估计下，数据删除模型下与LIU估计下线性模型参数估计量间的关系，并得到两者间的关系式.并利用修正LIU估计下得到的诊断统计量的表达式来判别强影响点.通过上面讨论，通过Di统计量得到第2，4，9号数据点是强影响点，与文献[1]中的结论相比，文献[1]只识别了第9号数据点作为强影响点，而本文通过加入先验信息，在修正的LIU估计下，利用更强的信息，不仅找出了第9号强影响点，还得到了其他两个强影响点.因此，Cook统计量对诊断强影响点具有统计意义.

参考文献

[1]王松桂，陈敏，陈立萍.线性统计模型线性回归与方差分析[M].北京：高等教育出版社，1999.

[2]林路.协方差阵扰动模型岭估计的影响分析[J].工程数学学报，1995，12（3）：83-88.

[3]叶仁玉，曾建军.广义岭估计优于最小二乘估计的两个充分条件[J].大学数学，2006，22（6）：66-69.

[4]刘栋富，田保光.广义岭估计的方差最优性质[J].科学技术与工程，2008（20）：5642-5643.

[5]王松桂.主成分的最优性与广义主成分估计类[J].应用概率统计，1985（1）：23-30.

[6]LIU K.A new class of biased estimate in linear-regression[J].Communications in Statistics Theory& Methods，1993，22（2）：393-402.

[7]殷艺芸.线性模型中LIU估计及两参数估计的进一步研究[D].重庆：重庆大学，2012.

[8]黄文焕，戚佳金，黄南天.带线性约束的回归模型参数的LIU估计[J].系统科学与数学，2009，29（7）：937-946.

[9]SWINDEL B F.Good ridge estimators based on prior information[J].Commun Stat Theory Methods，1976，A5（11）：1065-1075.

[10]LIYL，YANGH.AnewLiu-typeestimatorinlinearregressionmodel[J].StatPap，2012，53（2）：427-437.

[11]汪国平.线性模型中两参数估计及Jacknifed岭估计的进一步研究[D].重庆：重庆大学，2014.

[12]韦博成，鲁国斌，史建清.统计推断引论[M].南京：东南大学出版社，1991.

[13]张莉莉，张尚立.线性回归模型LIU估计的影响分析[J].科学技术与工程，2010，10（9）：2049-2051.

[14]张尧庭，方开泰.多元统计分析引论[M].北京：科学出版社，1982.

Strong Impact Analysis of Data Delete Model Based on Modified LIU Estimator

ZHU Ning,LIU Qinghua
（School of Mathematics and ComputingScience,Guilin Universityof Electronic Technology,Guilin 541004,Guangxi,China）

Strong impact analysis of multiple data delete model based on modified Liu estimator is studied.The property of estimators is discussed for the data deletion model.Furthermore,the relation between modified Liu estimator and Liu estimator is obtained.The prediction can also be estimated byMLEand yi,and so on.Besides,the new expressions of CRi,Cook estimator is given on the basis of the former.Finally,the Cook estimator is used to identify the strong impact point in one case,and verify its rationality.

modified Liu estimator;data deletion model;Cook estimator;strong impact point

O212.1

A

1001-4217（2017）01-0030-08

2016-03-03

朱宁（1957—），男，湖南宁乡人，教授，研究方向：线性统计模型。刘庆华（1990—），女，广西平乐人，硕士研究生，研究方向：应用统计。E-mail：lqh_1220@163.com