一种具有鲁棒性的子空间盲信道估计算法
刘 洋
(91550部队 大连 116023)
一种具有鲁棒性的子空间盲信道估计算法
刘 洋
(91550部队 大连 116023)
针对确定性盲信道估计算法在信道阶数未知条件下性能恶化问题,该文提出了一种对于信道阶数过估计具有鲁棒性的子空间盲信道估计方法。在信道阶数过估计条件下,基于传统子空间算法的理想解具有一定稀疏特性,该文通过增加加权约束条件并利用FOCUSS算法重构恢复其稀疏解。同时,为了避免算法中病态性问题的出现,引入增广拉格朗日函数法来改善算法稳健性。理论分析和仿真表明,选择适当的加权因子可使论文算法在较大阶数过估计(过估计3阶以上)情况下保证信道估计性能稳健,算法性能具有较强的阶数过估计鲁棒性且优于现有其他算法。
子空间算法; FOCUSS算法; 增广拉格朗日函数; 阶数鲁棒性
Class Number TN911
1 引言
无线信道盲辨识方法无需发射机周期性的发送训练序列即可获得信道信息的估计,相比传统基于训练的方案可以明显提高信道的传输容量,同时减小相应传输带宽的需求。以子空间算法(Subspace algorithm,SS)[1]为代表的基于二阶统计量(Second-Order Statistics,SOS)确定性盲辨识算法由于其无需信源统计分布先验知识、具有显著有限样本收敛等特性,因此引起了信号处理领域学者的广泛关注。但确定性盲辨识算法需要精确的信道阶数信息,一旦阶数错误估计,信道估计性能退化严重[2]。
经典的信道阶数估计方法包括信息论准则算法[3]和基于接收信号空间分解的Liavas算法[4];随后,一系列具有更好阶数估计性能的算法相应提出[5~7]。但这些算法普遍存在的问题在于运算复杂度较高,大多以运算复杂度的提升来换取阶数估计性能的改善。在实际的通信环境中,由于信道状态的动态变化,信道阶数精确估计通常难以实现实时跟踪,但信道阶数的上界信息可以从延等参数中较易获取[6];最近,文献[8]提出了一种对信道阶数过估计具有鲁棒性的MCR(Modified Cross Relation)算法,其无需精确的信道阶数估计而仅需要获取上界信息即可实现信道的有效估计,但是该算法在低信噪比条件下的估计性能不理想。文献[9]基于CR算法在信道阶数过估计条件下解空间与信道真实值的内在关联,提出了一种基于FOCUSS(Foca1 Underdetermined System Solver)算法[10]的具有阶数过估计鲁棒性的CR算法(本文称为CR-FOCUSS算法),但算法的稳健性较差,实现信道估计所需信噪比较高。
本文提出了一种基于FOCUSS的具有阶数过估计鲁棒性的子空间算法(SS-FOCUSS算法),算法求解过程中仅需信道上界信息,和文献[8~9]一样无需阶数估计算法辅助。SS-FOCUSS算法首先获得SS算法中由噪声向量构建的Q矩阵的解空间,基于信道解空间在信道估计时具有的一定的稀疏特性,然后利用FOCUSS算法求解其稀疏解从而获得信道估计。同时为了避免病态问题的出现,引入增广拉格朗日函数法来提神所提算法的稳健性。
下文中,[·]H,[·]T,(·)+,E{·}等运算符分别表示共轭转置,转置,Moore逆和期望运算。矩阵A的列空间所张成的空间表示为span(A)。
2 算法模型和子空间算法
通过在接收端配置L根天线以波特率接收或者利用单天线利用过采样技术以L倍波特率对接收信号进行采样,可等价得到单输入多输出(Single Input Multiple Output,SIMO)信道。在确定性SOS盲信道估计算法中通常将SIMO信道建模等效为M阶有限长冲激响应滤波器(Finite Impulse Response,FIR),接收信号可以表示如下:
(1)
式中,yi(n)表示在第n时隙第i个子信道的接收信号;子信道系数向量hi=[hi(0),…,hi(M)]T;{s(k)}为发送的信号序列;vi(n)为加性高斯白噪声。连续N个时隙的接收信号的矩阵表示为
y(n)=HNs(n)+v(n)
(2)
对观测输出y(n)求取相关矩阵Ry=E{y(n)y(n)H}。
Ry=HNRsHNH+Rv
(3)
式中Rs=E{s(n)sH(n)},Rv=E{v(n)vH(n)}。对Ry进行特征值分解
(4)
式中,Us=(u0,…,uM+N-1)由λi,0≤i≤N+M-1对应的左奇异向量组成,其列空间张成信号子空间,Uv由λi,N+M≤i≤LN-1对应的左奇异向量组成,其列空间张成噪声子空间。由文献[1]中结论可知,信号子空间与噪声子空间具有正交性,同时信号子空间满足span{Us}=span{ΗN}。因此,可得如下等式成立
UvHΗN=0
(5)
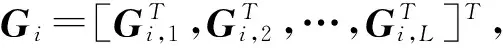
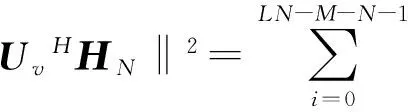
(6)
(7)
其中,c为随机向量。满足式(7)的解就是SS算法的信道估计。
3 基于FOCUSS的阶数过估计鲁棒子空间算法
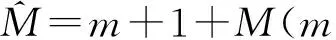
(8)
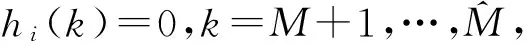
(9)
(10)
利用拉格朗日乘子法可转化为如下的无约束问题:
(11)
式(11)中的形式与FOCUSS算法类似。FOCUSS方法通过使得能量逐渐向解空间向量局部聚集因而获得具有稀疏形式的解。因此,可得如下信道系数的重构迭代公式:
(12)
通过引入增广拉格朗日函数法来求解优化模型。增广拉格朗日函数法通过构造精确罚函数,对增广因子的合适选择可以仅需较小的迭代次数使代价函数收敛到原问题最优解[13~14]。可以构造序列无约束优化问题:
(13)
引入增广因子βk可以对噪声有一定抑制作用。
(14)
通过推导可知:
(15)
可得如下信道估计的迭代重构方程
(16)
βk+1=β0(1+ka)a>0
(17)
式中,β0与a均为常数,拉格朗日乘子向量λ通过迭代方式获得:
(18)
4 仿真分析
实验中采用的仿真信道采用来源于文献[1]中的L=4,M=4的SIMO信道,信道系数如表1所示。仿真中发射信号为均匀分布的16QAM信号,叠加噪声建模为高斯白噪声。辨识结果的评价采用归一化均方根投影偏差(Normalized Root Mean Square Projection Misalignment,NRMSPM)[15],定义如下:
(19)

表1 信道系数
4.1 三种算法的估计性能对比
4.2 信道估计性能随过估计阶数ΔM和μ的变化实验
该小节研究所提SS-FOCUSS算法中ΔM和μ的变化对NRMSPM的影响。首先固定SNR=20dB,图4给出了NRMSPM随ΔM变化的曲线图。当加权参数选取为μ=0.002时,在ΔM较小时(ΔM≤2),NRMSPM小于-15dB;在ΔM较大时(3≤ΔM≤10),NRMSPM变化平缓并且小于-10dB,这表明SS-FOCUSS算法具有较强的阶数过估计鲁棒性,而MCR算法和CR-FOCUSS算法通常只能在高信噪比下且过估计阶数较少时性能较好。从图4中看出,随着μ的增大,SS-FOCUSS算法的NRMSPM随ΔM变化曲线逐渐恶化,说明μ的合适选取很关键。
图5中给出了不同信噪比条件下所提算法信道估计性能随μ与ΔM的变化图。图5(b)为在SNR=50dB条件下,当0.005≤μ≤0.02时,信道估计性能NRMSPM<-40dB;图5(c)为在SNR=70dB条件下,图5(c)中呈现出了L型区域,当0.005≤μ≤0.035时,信道估计性能NRMSPM<-50dB。同时发现图5(c)中L型区域面积较图5(b)中对应部分明显增加。仿真结果表明,加权因子μ的选取要求随着信噪比的增加可适当放松。
5 结语
本文提出了一种基于FOCUSS的具有阶数过估计鲁棒性的子空间算法。基于子空间算法在阶数过估计时理想解具有一定的稀疏特性,利用FOCUSS算法在给定的指数加权约束下迭代重构恢复信道系数的稀疏解,同时引入增广拉格朗日函数法提升算法稳健性。此外,本文算法中可采用文献[16]中方法降低子空间算法计算复杂度,而加快FOCUSS算法的收敛速度可以应用文献[17]中算法。理论分析和仿真表明,本文所提出算法性能优于现有其他算法;通过选取合适的加权因子可以使所提算法获得较强的阶数过估计鲁棒性。
[1] Moulines E, Duhamel P, Cardoso J F, et al. Subspace-methods for the Blind Identification of Multi-channel FIR Filters[J]. IEEE Transactions on Signal Processing,1995,43(2):516-525.
[2] 孙有铭,刘洛琨,等.一种基于FFT低复杂度的信道盲辨识算法[J].数据采集与处理,2014,29(3):378-383.
[3] Ridder F D, Pintelen R, et al. Modified AIC and MDL model selection criteria for short data records[J]. IEEE Transactions on Instrument and Measurement,2005,54(1):144-150.
[4] Liavas A P, Regalia P. On the behavior of information theoretic criteria for model order selection[J]. IEEE Transactions on Signal Processing,2001,49(8):1689-1695.
[5] 代松银,袁嗣杰,董书攀.基于子空间分解的信道阶数估计算法[J].电子学报,2010,38(6):1245-1248.
[6] Karakutuk S, Tuncer T E. Channel matrix recursion for blind effective channel order estimation[J]. IEEE Transactions on Signal Processing,2011,59(4):1642-1653.
[7] 孙有铭,刘洛琨,等.基于子空间信道矩阵迭代的阶数估计算法[J].电子与信息学报,2013,35(2):432-437.
[8] Shi M, Yi Q M. An efficient blind SIMO channel identification algorithm via eigenvalue decomposition[J]. Lecture Notes in Control and Information Sciences,2006,344(1):41-47.
[9] He Z S, Cichocki A. Robust channel identification using FOCUSS method[J]. Advance in Neural Network Research and Application,2010,67(1):471-477.
[10] Rao B D, Kreutz D. An affine scaling methodology for best basis selection[J]. IEEE Transactions on Signal Processing,1999,47(1):641-654.
[11] Meraim K A, Cardoso J F. On subspace methods for blind identification of single-input multiple-output FIR system[J]. IEEE Transactions on Signal Processing,1997,45(1):42-55.
[12] Schmid D, Enzner G. Cross-relation-based blind SIMO identifiability in the presence of near-common zeros and noise[J]. IEEE Transactions on Signal Processing,2012,60(1):60-72.
[13] Magnusr R. Multiplier and gradientmethods[C]//the Second International Conference on Computing Methods in Optimization Problems. San Remo, Italy,1968.
[14] 杨俊杰,刘海林.增广.lagrange函数优化算法在稀疏信号重构问题中的应用[J].计算机科学,2011,38(9):193-196.
[15] Dennis R. Morgan, Jacob Benesty, M. Mohan Sondhi. On the evaluation of estimated impulse responses[J]. IEEE Signal Processing Letters,1998,5(7):174-176.
[16] Koji H, Hideaki S. Blind subspace-based channel estimation using the EM algorithm[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei,2009:2797-2800.
[17] He Z S, Ciehoeki H A, Zdunek R, et al. Improved FOCUSS method with conjugate gradient iterations[J]. IEEE Transactions on Signal Processing,2009,57(1):399-404.
A Robust Subspace Method for Blind Identification
LIU Yang
(No. 91550 Troops of PLA, Dalian 116023)
Due to the performance degradation of deterministic blind channel identification algorithms under the overestimation of channel order, a FOCUSS-based subspace method is proposed for blind channel identification, which is robust to channel order overestimation. Based on the sparsity of the desirable channel estimation to order overestimation, a weighted constraint is used to search the sparse solution, combining with the FOCUSS algorithm, and then augmented Lagrange function is applied to improve the robustness of the FOCUSS algorithm. The simulation results show proposed algorithm owns better robustness to order overestimation than existing algorithms.
subspace method, FOCUSS algorithm, augmented Lagrange function, robustness to order overestimation
2016年8月12日,
2016年9月27日
刘洋,男,硕士,助理工程师,研究方向:信号处理。
TN911
10.3969/j.issn.1672-9730.2017.02.007

