可靠性安全系数法在结构静强度设计中的应用

马建章，高驰名

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

可靠性安全系数法在结构静强度设计中的应用

马建章，高驰名

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

针对传统静强度设计中常出现的结构失效、可靠性低等现象，研究应力-强度干涉模型的原理、安全系数与可靠性系数的关系，利用可靠度安全系数法来进行结构静强度设计，提高结构静强度可靠性。简要介绍了结构静强度设计的基本流程，说明了构件强度和应力分布类型以及参数的确定方法；详细介绍了应力和强度都符合正态分布的可靠度系数和概率安全系数的计算方法，并给出了可靠度安全系数的计算公式，提出了可靠性安全系数法实施步骤。以某设备为例，详细说明了如何利用可靠性安全系数法设计螺钉直径，并进行校核。试验证明该方法有效、可行。

可靠性安全系数法；结构静强度；应力-强度干涉模型

0 引言

机械结构静强度设计的传统方法是安全系数法，其基本思路是把结构的强度和应力看成确定量，二者的比值定义为安全系数。若安全系数大于或等于许用安全系数，则认为结构安全，可满足使用要求。但实际中按照安全系数法设计出的机械结构在其寿命周期内，仍然有某些构件失效。其根本原因在于它把各种参数都当作定值，没有分析参数的随机变化特性。应力-强度干涉模型将强度分布、应力分布和可靠性指标结合在一起，充分反映了强度和应力的分布特性与可靠性指标的关系。但该方法计算烦琐，计算过程不够直观，而且要求设计人员具备一定的概率论知识[1]。

本文在应力-强度干涉模型的基础上，将可靠性系数引入安全系数中，使安全系数与可靠性系数联系在一起，提出了基于可靠性的安全性系数的结构设计方法。该方法使安全系数能反映可靠度，克服了传统安全系数设计方法的不足，且便于工程人员使用。

1 应力-强度干涉模型

应力-强度分布干涉模型简称为干涉模型，它是零件可靠性设计的基本模型[2]，可以描述由外界的某种应力超过了该构件对此种应力所能承受的限度(强度)而引起的构件失效，其设计过程如图1所示。

图1 机械结构静强度可靠性设计过程

1.1 应力-强度干涉模型原理

可靠性分析理论认为结构承受的应力s和构件对应的材料强度r是服从某种分布状态的随机变量，并假设结构的应力和强度在统计意义上相互间独立，结构应力s和强度r的概率密度函数分别为f(s)和f(r),根据Birnbaum提出的结构可靠度计算方法，应力-强度干涉图如图2所示[3]。

图2 应力-强度干涉图

由统计分布函数的性质可知，应力和强度这2个概率密度函数在一定条件下可能发生相交的区域(图2中的阴影部分)就是零件可能出现失效的区域，称为干涉区[4]。一个零件是否可靠，就看其强度值和应力值的大小，如果零件的强度r>应力s，该零件能正常工作，则其可靠度就是事件强度r>应力s的概率，即：R=P(r>s)[5]。由图2有

(1)

由于存在干涉，任何设计都存在故障或失效的概率，可靠性设计就是要搞清楚零件的应力-强度的分布规律，严格控制发生故障的概率，以满足设计要求。

1.2 应力-强度分布类型和分布参数的确定

构件危险截面上的工作应力通常取决于载荷的大小、作用位置和时间、剖面的几何形状和几何参数、材料物理性质以及工作条件等。在静载荷情况下，应力主要取决于载荷和几何尺寸的变化。经大批实测数据的统计处理表明，各种几何尺寸，如长度和直径等，都较好地服从正态分布，其标准差可用3σ法则去估计。3σ法则同样也适用于确定载荷和应力等的标准差[6]。因此构件的应力一般服从正态分布，即使某些不是服从或不完全服从正态分布，也可以选择正态分布去估计，因为这样偏于安全。

零件材料的强度是抵抗失效的极限工作应力，与材料性质、热处理方式、应力种类以及其他很多因素(应力集中、表面质量、尺寸大小、工作温度和环境)有关。大量统计资料表明，材料的静强度，如屈服强度σs、强度σb都较好地服从正态分布。

1.3 应力-干涉模型可靠度的计算

当构件的应力s和强度r均服从正态分布时，有

(2)

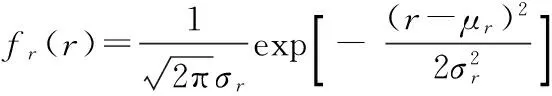
(3)

式中，fs(s)为使用应力的概率分布密度函数；μs为使用应力正态分布的均值；σs为使用应力正态分布的标准差均值；fr(r)为材料强度的概率分布密度函数；μr为材料强度正态分布的均值；σr为材料强度正态分布的标准差均值。

根据干涉概率的联合积分算法，其对应构件的可靠度为[7]：

R=φ(βR)。

(4)

式中，βR为可靠性系数，

(5)

除正态分布外，构件的强度和应力其他分布函数一般有对数正态分布、极值分布和威布尔分布等，其可靠度计算方法可参考相关文献。

2 结构静强度的可靠性安全系数法

可靠性安全系数法是同时考虑了零件的强度和载荷的分布特性与零件的安全系数，将零件的强度和应力的变异系数与可靠性系数相联系，引入到零件的概率安全系数中，使零件的概率安全系数成为一个可定量衡量可靠性的系数[8]。

2.1 概率安全系数

在某些装备结构的静强度设计中采用了概率安全系数法，其概率安全系数公式如下：

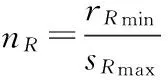
(6)

式中，nR为概率安全系数；rRmin为构件材料强度下限值；sRmax为构件应力上限值。

假设构件的应力和强度均服从正态分布，有

(7)式中，φ(X)为标准正态分布的概率分布函数；Rs为应力可靠度，一般机械结构设计规范，取Rs=99%；Rr为强度可靠度，一般机械结构设计规范，取Rr=95%；Cs=σs/μs为使用应力变异系数；Cr=σr/μr为材料强度极限变异系数；nm=μr/μs为中心安全系数。

2.2 可靠性安全系数法评定公式

将式(5)带入式(7)，得到构件可靠性系数与概率安全系数的关系式：

(8)

换算得到可靠性安全系数法对构件可靠性的评定公式[9]为：

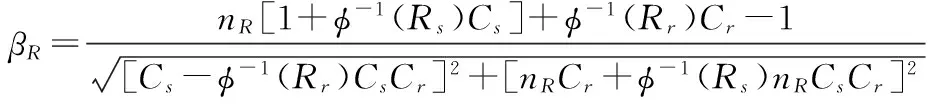
(9)

从以上公式可以看出，当给定μs后，为了提高结构可靠性，如果能降低σr和σs值，对于提高可靠性相当有效；如果提高μr值，显然会导致结构重量的增加[10]。

2.3 可靠性安全系数法实施步骤

基于可靠性安全系数法结构可靠性设计基本步骤如下：

① 选取安全系数，通常的安全系数取值依据有关强度规范确定，在先进的静强度可靠性设计中，则根据构件的静强度可靠性指标和载荷、强度变异系数，从nR-Cr曲线族中确定；

② 由使用载荷乘以安全系数，确定设计载荷；

③ 依据设计载荷，通过有限元法等应力分析方法确定构件的最大应力；

④ 在静强度设计时，以计算应力达到材料强度极限均值为条件，确定对应结构的尺寸；

⑤ 在设计后的静强度校核中，以强度极限均值与计算应力的比值作为静强度是否满足要求的依据，该值≥1则静强度合格，该值≤1则静强度不足。

3 设计实例

某设备通过两端凸台固定，外形示意如图3所示，结构参数如下：外形尺寸(宽×高×深)：150 mm×95 mm×80 mm；重量≤3kg。其中冲击要求为：峰值加速度：30g，脉冲宽度：11ms，脉冲波形：半正弦型脉冲。设计固定设备的螺栓(螺钉)，保证设备在受到垂直底面向上的冲击时，螺栓的静强度满足可靠性要求，分配到螺栓上的可靠性参数为：R≥0.999 9。假设设备为刚性，重心与设备结构形心重合，螺栓的载荷与强度均服从正态分布。

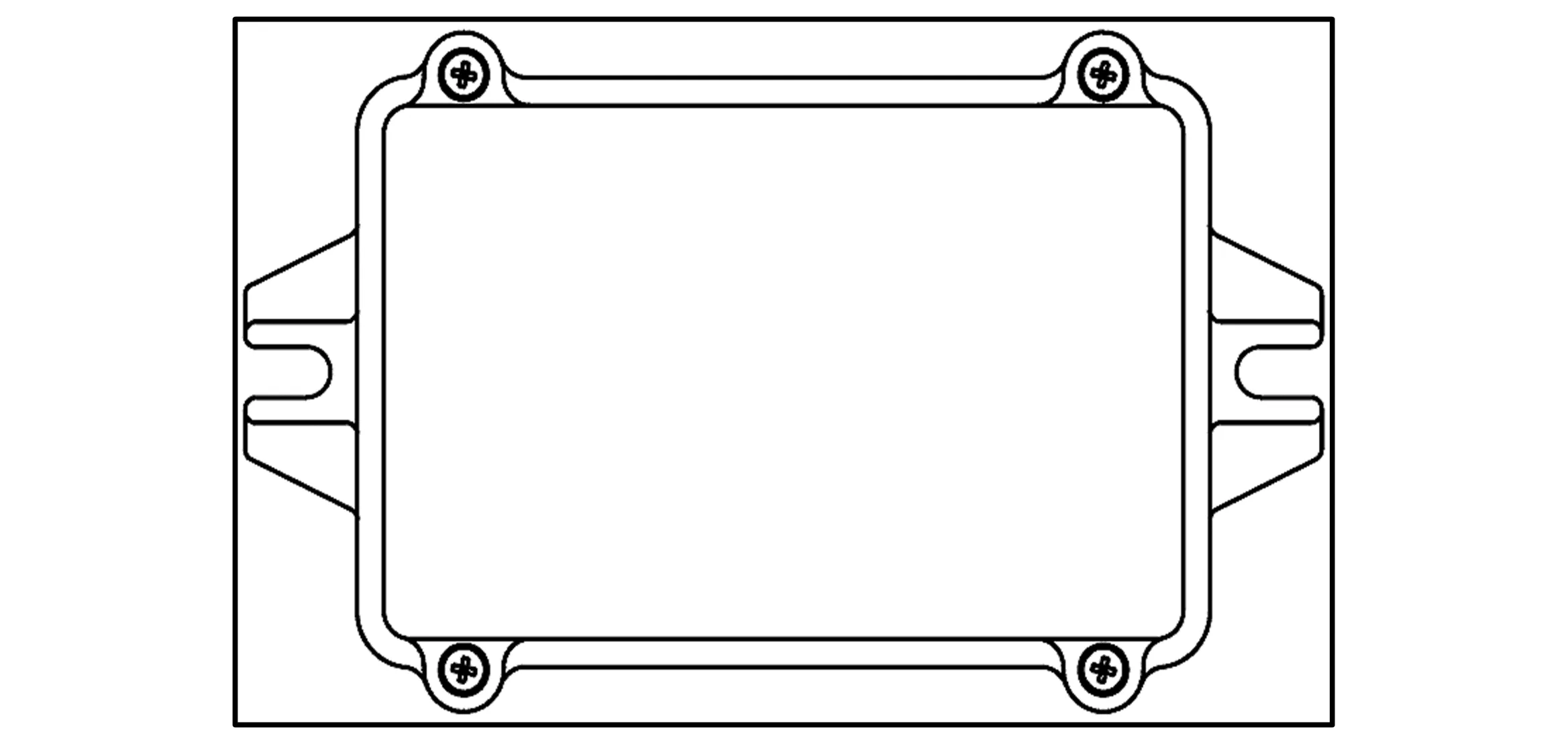
图3 设备外形示意

3.1 确定螺栓设计载荷

3.1.1 确定螺栓强度分布参数及变异系数

表1 紧螺栓连接参数的统计特征值

3.1.2 计算载荷的变异系数

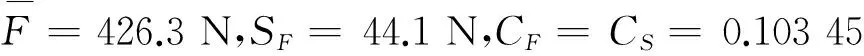
3.1.3 计算螺栓设计载荷

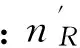
3.2 确定螺栓应力的分布参数及变异系数

3.2.1 计算总拉力的分布参数

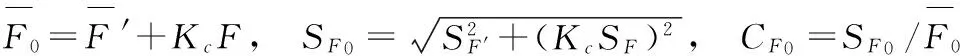
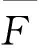
3.2.2 计算复合应力的均值、标准差及变异系数

① 计算螺栓拉应力、扭应力的均值、标准差和变异系数

螺栓扭应力标准差：

② 计算复合应力的均值、标准差

复合应力的均值为：

复合应力的标准差为：

变异系数：

3.3 设计螺栓直径

螺栓的和应力均值应小于螺栓的强度均值，则

查文献[12]，螺距为0.5mm的M3螺栓，小径为2.459mm，螺距为0.7mm的M4螺钉小径 3.242mm。采用M4螺钉即可。

3.4 校核螺钉静强度

螺钉复合应力均值为：

则螺栓的可靠度系数为：

则螺栓承受轴向冲击的可靠度为：φ(βR)=φ(4.04)=0.999 97，满足可靠性要求。因此采用M4螺钉紧固即可满足设备受到垂直方向冲击时的可靠性要求。同样的方法可以校核设备承受水平方向冲击时，螺钉是否满足可靠性要求。

4 结束语

可靠性安全系数法是以随机方法分析构件使用过程中的随机规律和可靠性问题，较充分、全面地利用设计信息，更能揭示构件可靠性分析的本质。较传统的安全系数设计方法，更能有效地利用构件的重量，减小构件的尺寸，从而在保证安全前提下节省材料，提高了构件设计的经济性。由于可靠性安全系数法与结构强度规范有着更直接的联系和继承性，便于结构设计人员采用，基于安全系数法的可靠性设计与评定可以作为结构静强度可靠性设计与评定的主要工程方法。

[1] 郭彦涛.电子设备可靠性设计[J].无线电通信技术，1998，24(5)：13-16.

[2] 孙志礼，陈良玉.实用机械可靠性设计理论与方法[M].北京：科学出版社，2003．

[3] 龚庆祥，赵 宇．型号可靠性工程手册[M]．北京：国防工业出版社，2007．

[4] 都军民，蔡 民，戴宗妙．基于可靠性安全系数的结构设计方法研究[J]．舰船科学技术，2007(6)：134-136．

[5] 杨瑞刚．机械可靠性设计与应用[M]．北京：冶金工业出版社，2008．

[6] 王 启，王文博．常用机械零部件可靠性设计[M]．北京：机械工业出版社，1996．

[7] 童团刚，张华全，谢崇全，等．机械零件静强度可靠性设计[J]．机械研究与应用，2009(3)：89-90．

[8] 李四超，张代国，张 强．机械结构可靠性计算方法[J]．舰船科学技术，2011(5)：63-65．

[9] 刘文珽．结构可靠性设计手册[M]．北京：国防工业出版社，2008．

[10]何昌寿．可靠性工程—设计、试验、分析、管理[M]．北京：宇航出版社，1989．

[11]GB/T3098.6-2000.紧固件机械性能不锈钢螺栓螺钉和螺柱[S]．

[12]GB/T196-2003.普通螺纹基本尺寸[S]．

马建章 男，(1982—)，工程师。主要研究方向：电子通信设备结构设计。

高驰名 男，(1982—)，工程师。主要研究方向：电子通信设备结构设计。

Application of Reliability Safety Coefficient Method on Design of Structure Static Strength

MA Jian-zhang, GAO Chi-ming

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

To solve the structure failure and the low reliability of structure, the principle of stress-strength interference model and the relation of safety coefficient and reliability were researched.The reliability of structure static strength was improved using reliability safety coefficient method.The basic flow chart of structure static strength is briefly introduced.This paper explicates the methods of defining parameters of stress and strength.The calculating methods of reliability coefficient and safety coefficient and the expressions are introduced.The implementation procedure of reliability safety coefficient method is put forward.Taking a type of equipment as an example, it expounds the method of designing bolt diameter by reliability safety coefficient method and checks the result.The test has proved the method is effective and feasible.

reliability safety coefficient method;structure static strength;stress-strength interference model

10.3969/j.issn.1003-3106.2017.03.20

马建章,高驰名.可靠性安全系数法在结构静强度设计中的应用[J].无线电工程,2017,47(3):79-82.

2016-11-17

河北省重点研发计划项目新一代电子信息技术专项基金资助项目(16210327D)。

TB114

A

1003-3106(2017)03-0079-04