三角形相似的解法与技巧

牟杰

一、相似三角形常见类型

对于几何题，只要条件稍加变化，或者图形稍作改动，就会成为一个新的题目，但若能抓住要点，进行归纳分类，就能抓准其中解答的关键，从而理清思路，简化证明的步骤。

相似三角形常见基本类型有：平行型、斜交型、垂直型和旋转型四类.针对不同类型，在解答时应掌握以下几种常见思路：

1.平行型：条件中若有平行线，可直接得两三角型相似，如没有平行线，可添加平行线，构造平行型相似三角形。

例1：如图，DE//BC，则△ABC∽△ADE

2.斜交型：条件中若有一对角相等，可考虑在找一对角相等，应用相似三角形方法1（两角对应相等的两个三角形相似），或找等角的夹边对应成比例，应用相似三角形的方法3（两边对应成比例且夹角相等的两个三角形相似）。

例2：

如图，若∠1=∠B，或∠2=∠ACB，则△ABC∽△ACD（或△ABC∽△ADE）

3.垂直型：若有一对直角出现在条件中，可考虑再找一对等角，使用方法1；或者证明斜边、直角边对应成比例.

例3：

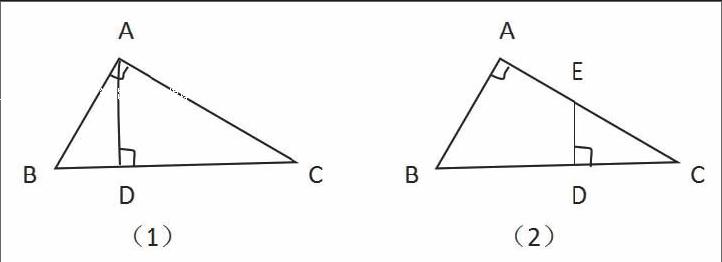
如图（1），AB⊥AC，AD⊥BC，则△ABD∽△CBA∽△CAD；

如图（2），AB⊥AC，ED⊥BC，则△ABC∽△DEC

4、旋转型：条件中若有两边对应成比例，可寻找夹角相等，应用相似三角形的方法3，常见于旋转型题目中；或设法证明第三对边与其他两边对应成比例，应用相似三角形方法2（三边对应成比例的两个三角形相似）.

例4：如图，∠1=∠2，∠3=∠4，则△ABD∽△ACE.

解：（略）

对于上述基本图形，在不同题目中尽管可采用不同方法，

但其中的思考方式是完全一致的.

二、相似三角形探索试题举例

在近几年的中考试题中，出现了很多有关相似三角形的探索试题，现整理几例，供学习.

1.数一数

例1：如图，锐角△ABC的高CD和BE交于点O，

图中与△ODB相似的三角形的个数是（ ）

（A）1 （B）2 （C）3 （D）4

分析：图中的∠A=∠BOD=∠COE，因此与△ODB相似的三角形有△ABE、△COE、△ACD，答案为（C）.

2.想一想

例2：将两块完全相同的等腰直角三角板摆放成如图的样子，假设图形中的所有点、线都在同一平面内，回答下列问题：

（1）图中共有多少个三角形？

（2）图中有相似三角形吗？如果有，把它们一一写出来.

解：（1）图中共有7个三角形

（2）图中有相似三角形.

∵△ABC、△AFG都是等腰直角三角形，

∴∠B=∠DAE=∠C=45°，

∵∠ADC=∠EDA，∴△BAE∽△ADE，

同理可得：△BAE∽△CDA、△ADE∽△CDA.

3.截一截

例3：点P是△ABC中AB边上的一点，过点P作直线（不与直线AB重合）截△ABC，使截得的三角形与原三角形相似，满足这样条件的直线最多有 条。

解：如图所示，满足条件的直线共有四条。

4.填一填

例4：如图，∠1=∠2，请补充条件：

（写出一个即可），使△ABC∽△ADE.

分析：∵∠1=∠2，∴∠EAD=∠BAC，

则当∠B=∠D或∠C=∠E或时，

都可以使△ABC∽△ADE.

5.找一找

例5：如图，已知△ABC、△DEF均为正三角形，D、E分别在AB、AC上，请找出一个与△DBE相似的三角形并证明.

分析：△ECH与△DBE相似.理由如下：

∵△ABC、△DEF为正三角形，∴∠B=∠C=∠DEF=60°，

∴∠BDE+∠BED=120°，∠CEH+∠BED=120°，

∴∠BDE=∠CEH，∴△ECH∽△DBE.

注意：除了△ECH外，圖中△ADG、△FHG也与△DBE相似.