分形图案在电脑提花针织面料上的应用

路丽莎， 宋晓霞

(上海工程技术大学 服装学院，上海 201620)

研究与技术

分形图案在电脑提花针织面料上的应用

路丽莎， 宋晓霞

(上海工程技术大学 服装学院，上海 201620)

图案是针织面料不可或缺的艺术表现语言，针织面料的图案可以由组织结构和色彩来表现，色彩图案也即提花。针对目前针织面料的图案主要是由传统图案构成的问题，文章根据分形图案的不同生成原理，利用C++语言编写了基于生成元和逃逸时间算法的分形图案，并在电脑横机的花型设计软件中对生成的图案进行二次设计，最后将设计好的花型程序导入电脑横机中进行实际的编织。结果表明：基于生成元生成的分形图案可以重新排列组合后应用在针织提花面料上，基于逃逸时间算法生成的分形图案可以以局部或满花的形式应用在提花面料上。

分形图案；二次设计；电脑横机；针织面料；提花面料；编织

图案可以对面料进行修饰和点缀[1]，对于针织面料而言，图案常用色彩图案即提花来表现。提花就是按照花纹要求，选择某些织针进行编织成圈而形成的带有花纹图案的组织，一行有几种颜色就叫几色提花，随着纱线颜色数的增多，织物会越来越厚。分形图案是一种复杂的、不规则的图形，利用其独特的特性，可以构造出千变万化的艺术图案，从而为针织面料图案设计提供灵感。本文根据分形图案不同的生成原理，从基于生成元和逃逸时间算法的分形图案出发，研究其在针织提花面料中的应用。

1 分形图案概述

分形是用来描述自然界中存在的粗糙和不规则的几何形体，如动物的血管、起伏的山脉、漂浮的云朵等。分形是由计算机创作生成的，由于其独特的美学特征，在物理、建筑及艺术等领域有着广泛的应用。分形主要有以下几个特征[2]：

自相似性：指分形在生成过程中产生出许多和自己相似的部分；不规则性：是指它的整体和局部都不能用传统的几何语言来描述，它既不是满足某些条件的点的轨迹，也不是某些简单方程的解集；精细性：分形图案具有精细的结构、蕴涵着无穷的嵌套结构，在放大任意倍数下，也具有复杂的结构形态；多样性：分形图案是通过计算机结合数学理论产生的新型图案，不受想象力、时空的限制[3]。正是由于这些特点，如果将分形图案应用在针织面料图案设计上，能极大地改变面料的视觉效果，给针织面料图案设计带来新的设计灵感。

2 电脑提花程序的设计

2.1 提花图案的花型设计

分形图案的不规则性和复杂性决定了其不能直接应用在针织提花面料的图案设计中，这就需要对其进行二次设计，使之成为符合针织面料图案设计类型。本文借助Stoll电脑横机的花型设计软件Stoll-M1plus，对图案进行二次设计。电脑横机是一种具有双针床选针功能的针织设备针织机械，所编织物属于纬编的一种，生产效率高、花型变化丰富，是技术含量较高的服装设备[4]。

将计算机生成的图片保存为bmp格式，导入花型设计软件中。首先对其进行去色处理，由于电脑横机中一个导纱嘴代表一种颜色的纱线，因此在设计花型时要确保每行的颜色数应相同，否则编织出的面料会厚薄不匀，但各行的颜色可以不同，一般来说，提花织物的颜色不超过四色。对分形图案而言，由于其不规则性难以保证在设计的过程中每行的颜色数恰好都相同，这时要对其进行边缘处理，即在颜色数少的行的边缘增加一两列其他颜色到所需颜色数，从而达到每行颜色数都相同的效果。其次，若是做连续图案，则可以根据要求进行对称、翻转等变化。

2.2 提花图案的程序生成

提花的花型设计好以后就可以定义提花的结构，即确定所编织物的组织结构；对同一花型，不同的组织结构有时会直接影响花型效果。单面提花由于背面存在浮线，适用于一些规则、色块分割较小的图案编织，而分形图案适用于双面提花编织。双面提花背面有多种组织，可以根据设计要求进行选择。提花结构定义好后，只能用定义好后的提花颜色画图，不能使用其他的纱线颜色和线圈作图。若要修改提花图案或组织类型，还需回到提花结构定义前；其次就是对程序做分离纱和封口纱，分离纱要做在织物的前两行，而封口纱做在大身编织完的最后两行，任何织片的结束处都要加封口纱[4-5]。最后进行纱嘴分配和导出程序，此时就生成了一个可以用于上机编织的完整的提花程序。

3 分形图案在针织提花面料上的应用

分形图案的生成方法有多种，本文主要研究基于生成元和逃逸时间算法生成的分形图案及其在双面针织提花面料中的应用。

3.1 基于生成元生成的分形图案

基于生成元生成的分形图案本质上是一种迭代的算法，即给定基本元素和变化规律，反复多次递归、迭代后生成缤纷无限的分形图案[6]。基本元素既可以是线也可以是面。

3.1.1 以线作为生成元的分形图案

以线作为生成元可以生成很多分形图案，如以一条线段为基元，第一次从该线段中点折叠成夹角为90°的两条线段，第二次分别从两条线段的中点向相同方向折叠90°。经过多次折叠后就形成了漂亮的分形图案，这就是著名的莱维C形曲线[6]，如图1所示。

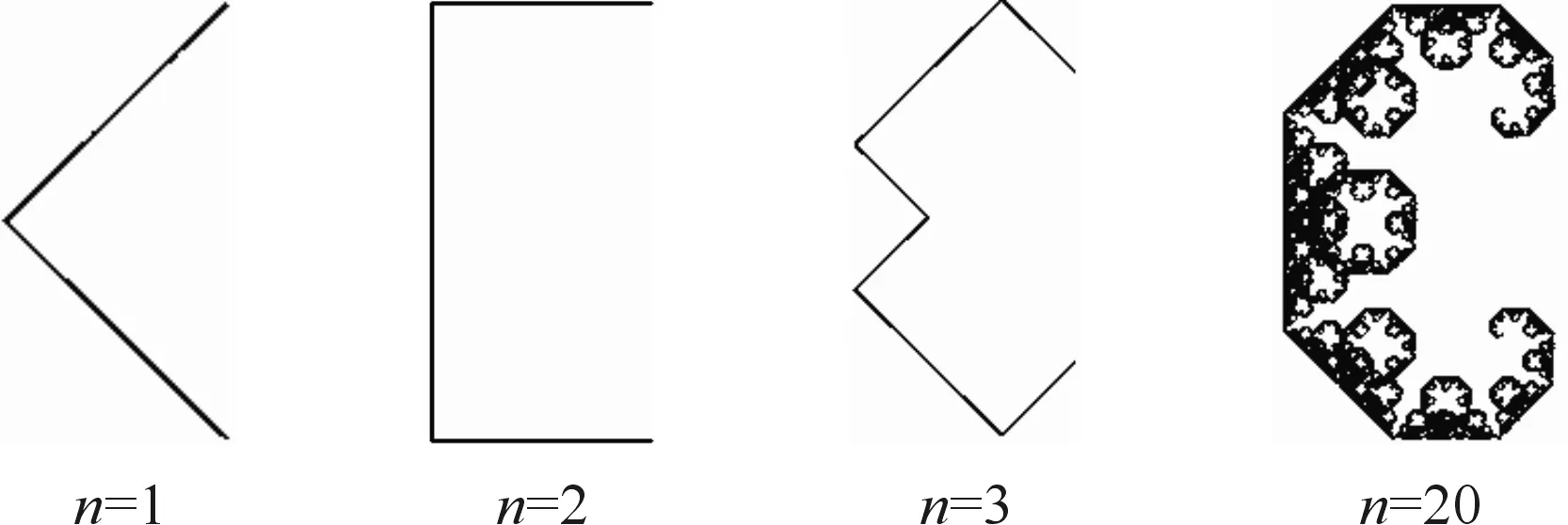
图1 莱维C形曲线Fig.1 C shape curve of Levy

这类图案的主要特点就是色彩简单且随着迭代次数的增加，内部结构会越来越精细，适宜做连续图案，两色便可以显示其主要特点。以背面为芝麻点和横条组织进行编织，芝麻点组织是每一个反面横列由两种色纱交替编织，背面呈现散点式的分布，属于不完全提花组织；而横条组织每一成圈系统所有的反面线圈对应织针都进行编织，背面呈现横条状，属于完全提花组织[7]。因此，横条组织的正反面的纵密比大于芝麻点组织，在编织的过程中图案容易变形(易被拉长)，不宜应用于双面提花的编织，如图2所示。

图2 莱维C曲线实物案例Fig.2 Object case of Levy C curve

3.1.2 以面作为生成元的分形图案

以面作为生成元是以某一个面元素作为基元，在其基础上根据一定的规律反复迭代后生成的一系列图案。如以60°菱形为构成元素，从第二次开始以1︰2的大小在四个顶点处衍生小的菱形，如果某一顶点是其“父”则不衍生，依次下去就会生成一个较复杂的图案，如图3所示。

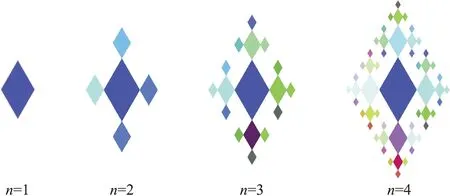
图3 菱形格Fig.3 Diamond lattice

该图案的最大特点是很规则，根据图案就可以看出其迭代规律，在针织面料图案设计中，图案越规则，可选择的工艺就越多。以n=4的图形为例，选择较复杂的翻针工艺进行编织，这是一种特殊的提花，翻针区域的色纱不再参加编织，而是由其他色纱在后针床编织反面线圈形成花型。因此，翻针的地方较薄，凹凸对比形成了立体感。另外，通过组织结构对色块进行分割，减少了纱线数的使用，降低了织物的厚度。本文采用芝麻点翻针和横条翻针两种工艺编织，芝麻点翻针在翻针部位及反面呈散点分布，而横条翻针在翻针部位及反面呈横条状，如图4所示。显然，横条翻针图案变形较大、卷边性比较明显，因此实际编织中不宜采用。

图4 菱形格实物案例Fig.4 Object case of diamond lattice

3.2 基于逃逸时间算法生成的分形图案在提花面料上的应用

逃逸时间算法是一种基于迭代法的画图法，假设f是一个变换，f的n次迭代fn为f0(x)=x，f1(x)=f(x)，fn+1(x)=f(fn(x))，n=0，1，2…。逃逸时间算法的生成原理就是在计算机中确定图形区域并建立坐标系，将区域中像素的坐标依次代入到相应的迭代公式中，并计算该像素点的坐标在给定的迭代次数下是收敛还是发散；将区域收敛的像素用一种颜色表示，发散的像素用另一种颜色表示，在给定的迭代次数下由于每个像素点收敛的迭代次数不同，发散的迭代次数也不同，这样分别添加不同的颜色就得到了绚丽多彩的分形图案。逃逸时间算法下生成的图案有经典的Mandelbrot集、Julia分形集及Newton迭代分形等，其主要特点就是色彩绚烂、结构复杂、对任一个局部放大均会出现复杂的图案。

3.2.1 局部形式的应用

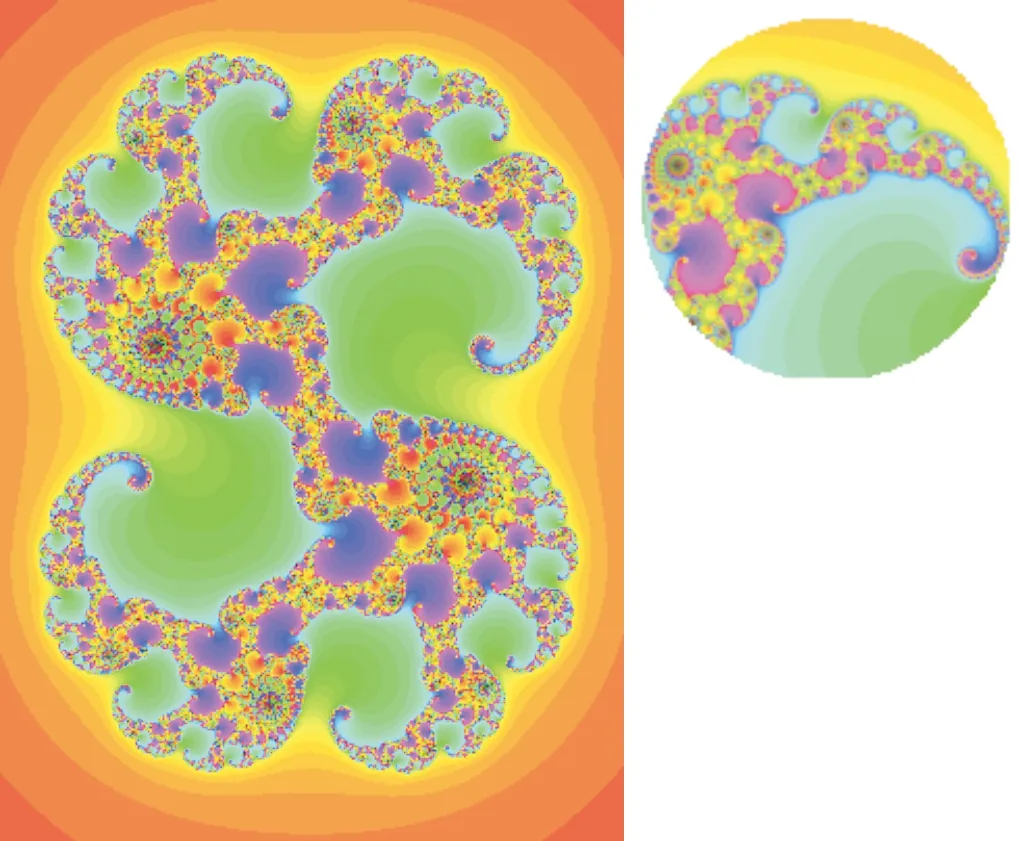
图5 Julia分形图案Fig.5 Julia fractal pattern

图6 Julia集正面示意Fig.6 Front diagram of Julia set

图7 Julia集反面示意Fig.7 Back diagram of Julia set

3.2.2 满花形式的应用

所谓满花形式就是将计算机生成的整个图案应用于针织面料的图案设计中。以Newton迭代分形为例，牛顿分形是依据牛顿迭代公式zn+1=zn-f(zn)/f′(zn)而生成的图案[10]，f(x)可以为任意基本函数，当函数不同时，生成的图案也不同。图8所示的f(x)=tanx时的图案，该图案本身就是一种连续图案，可以以满花的形式应用在针织面料的图案设计中。

图8 Newton迭代分形图象Fig.8 Newton iteration fractal pattern

为了更清晰地表现图8的花型效果，设计了4种颜色的花型，如图9所示。由于4色双面提花织物比较厚，而抽针网络组织能达到保持原有花型和降低厚度的双重效果，且抽针次数越多，织物就越薄，所以选择网络及网络1×2进行编织。两种组织相比，正面效果完全一样，网络1×2反面花纹清晰度降低，织物的厚度减少但并不疏松，如图10所示。因此，对于4色提花来说，抽针网络提花可以应用，甚至可以做1×3抽针处理。从保暖的角度选择网络组织编织，从节约成本的角度选择抽针网络编织。

图9 Newton迭代分形正面示意Fig.9 Front diagram of Newton iteration fractal

图10 Newton迭代分形反面示意Fig.10 Back diagram of Newton iteration fractal

4 结 语

通过C++生成多种分形图案，将生成的分形图案运用电脑横机花型软件设计出针织提花程序，最后采用不同的工艺进行了编织，并比较分析了每种工艺的特点。通过将分形图案应用在提花面料图案设计上，不仅打破了传统针织面料图案设计的局限性，而且以更有新意、美感的优势，为针织面料的图案提供了新的设计方法和创作灵感，从而也进一步扩大了分形图案的应用领域。

[1]于超.基于分形的艺术图案生成方法的研究与应用[D].济南:山东师范大学,2007:26-27.YUChao.ResearchandApplicationsoftheArtisticGraphicsGenerationMethodBasedonFractalTheory[D].Ji’nan:ShandongNormalUniversity,2007:26-27.

[2]蔡燕燕.分形几何在服装图案设计中的研究与应用[D].上海:上海工程技术大学,2011:4-7.CAIYanyan.ResearchandApplicationofFractalGeometryinFashionDesign[D].Shanghai:ShanghaiUniversityofEngineeringScience,2011:4-7.

[3]徐向红.分形理论在服饰图案设计中的应用基础研究[D].长春:吉林大学,2009:17-34.XUXianghong.AppliedBasicResearchofFractalTheoryinClothingPatternDesign[D].Changchun:JilinUniversity,2009:17-34.

[4]姜晓慧,王智.电脑横机花型设计实用手册[M].北京:中国纺织出版社,2014:65-68.JIANGXiaohui,WANGZhi.InstructionManualofComputerizedFlatKnittingMachinePattern[M].Beijing:ChinaTextile&ApparelPress,2014:65-68.

[5]朱文俊,郑建林.电脑横机编织技术[M].北京:中国纺织出版社,2011:265-275.ZHUWenjun,ZHENGJianlin.ComputerFlatKnittingMachineKnittingTechnology[M].Beijing:ChinaTextile&ApparelPress,2011:265-275.

[6]吴运兵.分形理论在计算机图形设计中的研究与应用[D].西安:西安科技大学,2004:21-32.WUYunbing.ApplicationsofFractalTheoryinComputerGraphicsDesign[D].Xi’an:Xi’anUniversityofScienceandTechnology,2004:21-32.

[7]裘玉英,陈天里.电脑提花针织物组织结构设计及性能分析[J].丝绸,2013,50(2):35-38.QIUYuying,CHENTianli.Structuredesignandperformanceanalysisofcomputerjacquardfabricorganization[J].JournalofSilk,2013,50(2):35-38.

[8]万爱兰,缪旭红,丛洪莲,等.纬编技术发展现状及提花产品进展[J].纺织导报,2015(7):35-39.WANAilan,MIUXuhong,CONGHonglian,etal.Developmentstatusofweft-knittingtechnologyandrelatedjacquardproducts[J].ChinaTextileLeader,2015(7):35-39.

[9]唐颖,房宽峻.分形在数字喷墨印花图案设计中的应用[J].纺织导报,2009(6):112-115.TANGYing,FANGKuanjun.Applicationoffractalinthepatterndesignofdigitalink-jetprinting[J].ChinaTextileLeader,2009(6):112-115.

[10]丁玲聪,张聿.应用广义牛顿迭代图形的丝巾纹样设计方法[J].丝绸,2015,52(11):47-51.DINGLincong,ZHANGYu.DesignmethodofscarfpatternswithGeneralizedNewtoniterationgraphics[J].JournalofSilk,2015,52(11):47-51.

Application of fractal pattern in computer jacquard knitted fabric

LU Lisha, SONG Xiaoxia

(Fashion College, Shanghai University of Engineering Science, Shanghai 201620, China)

Pattern is the indispensable artistic language of knitted fabric. The pattern of knitted fabric can be expressed by structure and color. Color pattern is also jacquard. Since current knitted fabric patterns are mainly composed by traditional patterns, the paper applies C++ language to program fractal pattern based on generating element and escaping time algorithm according to the different generating principles and then redesigns the pictures in the pattern design software of computerized flat knitting machine. Finally, the designed pattern program is inputted to computerized flat knitting machine for practical weaving. The result shows that the fractal pattern generated on the basis of generating element can be rearranged and recombined, and then applied in knitted jacquard fabric. The fractal pattern generated on the basis of escaping time algorithm can be applied in jacquard fabric in the form of partial or full followers.

fractal pattern; secondary design; computerized flat knitting machine; knitted fabrics; jacquard fabric; knitting

10.3969/j.issn.1001-7003.2017.02.006

2016-05-12;

2016-12-11

路丽莎(1989-)，女，硕士研究生，研究方向为针织服装的研究。通信作者：宋晓霞，教授，songxiaoxiavivi an.@126.com。

TS181.8

A

1001-7003(2017)02-0025-05 引用页码: 021106