双向地震作用下的双排桩边坡参数敏感性分析*

董必昌 付绍卿 张 哲

(武汉理工大学交通学院 武汉 430063)

双向地震作用下的双排桩边坡参数敏感性分析*

董必昌 付绍卿 张 哲

(武汉理工大学交通学院 武汉 430063)

以门式双排抗滑桩为例，采用有限元软件Ansys建立仿真模型，通过改变模型中桩长、桩排距、桩间距，以及土的抗剪强度参数，对门式双排桩边坡在双向地震波作用下的受力性状进行了研究，结果表明，在动力作用下，当桩的锚固长度小于等于H/2时，静动峰值弯矩，桩身最大剪力和桩侧最大土压力会随抗滑桩锚固深度增加而增加，而当锚固长度大于H/2时，这3种力学效应均增长减缓，之后开始缓慢减小；当门式双排桩的桩排距在5.5 m时，静动峰值弯矩与桩侧土压力最大，其后随着桩排距增大逐渐减小；当双排桩间距为4倍桩截面宽度时，桩间的土拱效应最为显著；滑体土及滑带粘聚力c(25 kPa)和内摩擦角φ(24.1°)逐渐增大时，边坡稳定性提高;当达到1.2倍时, 静动峰值弯矩、桩身最大剪力，及桩侧最大土压力降低幅度最大，其后趋于平缓.

双向地震作用；门式双排桩边坡；参数敏感性分析；有限元

0 引 言

伴随着我国公路建设的高速发展，地质灾害防治已成为防灾、减灾领域中十分重要的一环，而在一系列边坡防灾措施中，抗滑桩对于抵御边坡滑移的效果明显，因此，在大中型滑坡整治工程中得到了广泛应用.与之对应的是，对于地震作用下抗滑桩的力学效应，国内外学者也展开了一系列的研究，得出了一些有价值的规律.衣伟[1]研究了在地震引起岸坡永久变形的情况下码头单桩的反应，以及抗滑桩在地震作用下的不同破坏形式.Maheshwari等[2]利用三维非线性数值计算程序研究了土与桩基础地震动力相互作用的模型，指出地震动力的相互作用增大了桩顶的反应却很大程度地减小了上部结构的动力效应.Takewaki 等[3]对桩-土地震动力的相互作用进行了深入研究，指出了群桩效应对其较大的影响力.年廷凯等[4]发表了抗滑桩加固土质边坡中抗滑桩四周土体的侧向容许承载力的下限解法.汪鹏程等[5]研究了强震作用下挡土墙、预应力锚索及抗滑桩等3种支护结构下边坡的动力响应，但是条件为土质边坡、单排桩，以及单向地震作用.张建经等[6]研究了高烈度地震区高陡边坡抗滑桩板桩墙在强震作用下的动力响应，研究对象为板桩墙.

上述研究主要揭示了地震波对抗滑桩的动力影响规律，地震波荷载大多采用单向输入或研究对象为单排桩，对于双向地震作用下门式抗滑桩边坡的参数敏感性分析研究较少，因此，文中以门式双排桩边坡为例，运用有限元数值模拟的方式，通过分别改变桩和土的相关参数，分析了其在双向地震波作用下的动力效应，得出了相关结论.

1 数值分析模型

1.1 模型概况

选用宝成线某典型折线滑面滑坡进行仿真模拟[7].该路段边坡山顶高程高于坡脚基坑开挖地平面30～53 m，主要由粉质粘土与含卵石粉质粘土构成土质边坡，地形坡度为23°～26°.此断面滑带厚度约为1 m，主滑动面长度为46.5 m，主滑动面倾角为23°.采用方形桩治理，桩身及纵梁的矩形截面尺寸为1.5 m×2 m，桩间距为5 m.锚固深度为1/2桩长.

边坡断面简化几何模型见图1，抗滑桩为门式双排桩，其尺寸及布置方式见图2.

图1 边坡抗滑桩示意图(单位：m)

图2 抗滑桩几何尺寸图(单位：m)

1.2 模型建立

模型中滑体土、滑坡带和基岩均采用8节点实体单元Solid45单元来模拟，抗滑桩则采用Ansys中用来模拟钢筋混凝土的Solid65单元.建模时桩身采用整体建模方式，桩身材料为C25混凝土，钢筋采用HRB335，将钢筋分布于整个单元中，将单元视为连续均匀材料.模型参数见表1.

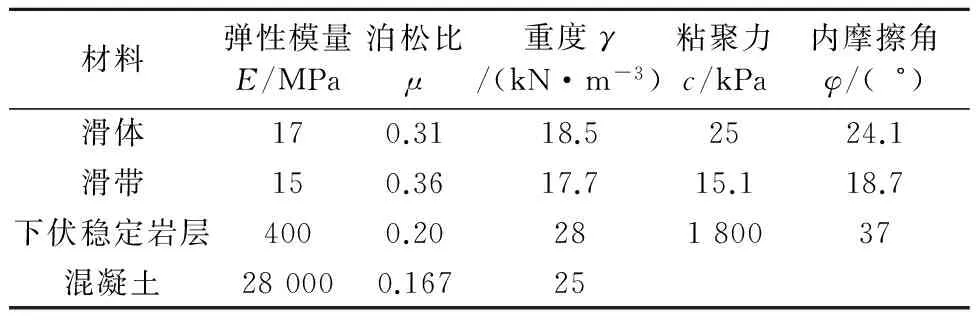
表1 滑坡体及抗滑桩材料参数

对于边坡的土体本构模型，文中采用理想弹塑性模型，屈服准则采用Drucker-Prager准则[8]；将桩视为线弹性体[9]；桩土之间设置接触，采用Ansys中的Targe170和Conta174来定义桩土模型中的接触对，从而建立了双排桩边坡模型，结果见图3.

图3 双排桩边坡模型

考虑到滑坡面为折线滑面，地层分界线为折线，利用工作平面将实体切割成便于划分网格的体，再对体进行网格划分.划分单元时，为兼顾计算精度和计算效率，采用六面体单元，同时对重点研究部位网格适当加密，次要部位划分稀疏的划分方式.网格划分后的有限元模型见图4.

图4 边坡网格划分图

在输入地震波前需对模型进行静力分析，通过静力计算得到边坡模型的初始应力状态和预变形后，将其作为地震分析的初始条件，再进行地震时程分析.静力分析时，边界条件为：基岩底面固定，边坡左右两侧水平方向约束，坡体表面为自由约束，初始应力条件为边坡自重应力；瞬态分析时，在边坡基岩处同时输入竖直方向和水平方向传播的剪切波和压缩波，此时边界条件发生改变，即删除边坡左右两侧的水平方向约束使两侧边界能自由变形，竖直方向设置连杆支座，基岩底部仍然为全约束.

1.3 地震波的施加

图5 EI-Centro地震波加速度时程曲线

文中边坡位于四川省某高烈度地震区，该地区的抗震设防烈度为8度[10].鉴于此工程场地的卓越周期不大，故采用EI-Centro地震波的NS方向和竖直方向，并对EI-Centro波进行幅值调整[11].幅值调整后的EI-Centro地震波加速度时程曲线见图5.地震波NS的地面峰值加速度为0.2g，竖直向地震波地面峰值加速度同比例缩减为为0.12g.模型的瑞利阻尼系数α=0.06，β=0.035.地震波的持续时间取包含其最大峰值的前8 s，时间间隔为0.02 s，共400个记录数据[12].

2 参数敏感性分析

2.1 桩参数的影响因素

2.1.1 桩长影响分析

为研究桩长变化对抗滑桩在地震作用下的受力影响，在桩排距d=5.5 m、桩间距D=5 m、双排桩每桩截面积为2 m×1.5 m、边坡土性质等条件不变的情况下，分别取抗滑桩桩长H=28，26，24，22 m(后排桩锚固深度分别为16，14，12，10 m).计算得到模型在地震作用过程中的受力和变形特性，选取双排桩边坡的3个重要力学性质，分别为：静动峰值弯矩，桩身最大切应力，桩侧最大土压力，对其进行比较，结果见图6～8.

图6 静动峰值弯矩与桩长的关系

图7 桩身最大剪应力与锚固深度的关系

图8 桩侧最大土压力与锚固深度的关系

由图6～8可知，并非桩嵌入基岩的锚固深度越深，在动力作用下桩身内力就越大或是越小，由图6可知，当桩身锚固长度小于等于H/2时，静动峰值弯矩会随门式抗滑桩锚固深度的增加而增加，当锚固长度大于H/2时，弯矩增长速度减缓，同时静动峰值弯矩随着锚固深度的增加而开始减小.由图7～8可知，桩身最大剪力和桩侧最大土压力随着锚固深度的增加也呈现这种趋势，且都在桩长H=26 m(后排锚固深度为14 m)左右时达到峰值.

2.1.2 桩排距影响分析

为研究桩排距d对抗滑桩和边坡的震后影响，在桩长H=28 m、桩间距D=5 m、双排桩每桩截面积2 m×1.5 m、边坡土性质等条件不变的情况下，分别取桩的(中心轴间距)前后排距d=5，5.5，6和6.5 m，通过计算得到不同排距的门式抗滑桩受力特征，进行比较分析，结果见图9～11.

图9 静动峰值弯矩与桩排距的关系

图10 桩侧最大土压力与桩排距的关系

图11 桩身最大剪应力与桩排距的关系

由图9～11可知，随着桩排距从5 m增至6.5 m，桩身静动峰值弯矩和最大土压力表现为先略微增大而后逐渐减小，在排距为5.5 m左右时达到极大值；而桩身最大剪力值则随排距的增大呈现逐渐增大的趋势.总体趋势可概括为：桩排距增大时，桩身最大剪力随着增大，而静动峰值弯矩和最大土压力则在减小，此趋势也表明此时抗滑桩的加固效果在逐渐减弱.

2.1.3 桩间(列)距影响分析

为研究桩间距D的影响，在桩长H=28 m、桩排距d=5.5 m、双排桩截面积2 m×1.5 m、边坡土性质等条件不变的情况下，分别取桩间距为：D=5，6，7，8 m，计算得到抗滑桩的震后受力变形特性，结果见图12～14.

图12 静动峰值弯矩与桩间距的关系

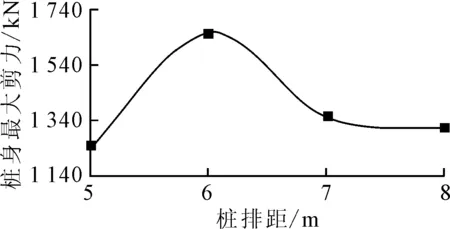
图13 桩身最大剪应力与桩间距的关系

图14 桩侧最大土压力与桩间距的关系

由图12～14可知，桩间距D对于桩土的动力响应的影响较大，属敏感参数.而桩间距从5 m增加至8 m时，静动峰值弯矩、桩身最大剪力和桩侧最大土压力均随桩间距增加后减小，在桩间距为6 m(即4b，b=1.5 m为桩截面宽度)左右时到达最大值.且在6 m时，桩间的土拱效应最为显著，此时门型抗滑桩加固边坡抵抗动力失稳的效果最好.当间距过大时，土拱效应不再明显；间距减小时，虽然整体动力加固效果更好了，但是桩根数增加，分配在单根抗滑桩上的滑坡力减小，同时也不经济.

2.2 土抗剪强度指标的影响

2.2.1 滑体土粘聚力c的影响

在双排桩参数不变，即取桩长H=28 m、桩排距D=5 m、桩间距d=5.5 m、双排桩每桩截面积为2 m×1.5 m、φ=24.1°情况下，取初始c=25 kPa，并依次增长c值的倍数，以此来研究滑体土(包括滑带)的粘聚力(c)的变化对抗滑桩动力结果的影响，计算得到抗滑桩的震后受力特性，进行比较，结果见图15～17.

图15 静动峰值弯矩与滑体土 粘聚力的关系

图16 桩身最大剪应力与滑体土 粘聚力的关系

图17 桩身最大剪应力与滑体土 粘聚力的关系

由图15～17可知，随着滑体土粘聚力逐渐增大，边坡稳定性提高，在动力作用下静动峰值弯矩、桩身最大剪力以及桩侧最大土压力都在减小，其中在滑体土粘聚力由25 kPa增大至30 kPa阶段，静动峰值弯矩与桩侧最大土压力减小速度非常快，之后速度放缓，整个减小的趋势呈折线形.

2.2.2 滑体土内摩擦角φ的影响

在双排桩参数不变，即取桩长H=28 m、桩排距D=5 m、桩间距d=5.5 m、双排桩每桩截面积为2 m×1.5 m、滑体土粘聚力c=25 kPa情况下,取初始φ=24.1°，并依次增长φ值的倍数来研究滑体和滑带土的内摩擦角(φ)变化对抗滑桩动力结果的影响，计算得到抗滑桩的震后受力变形特性，并进行比较，结果见图18～20.

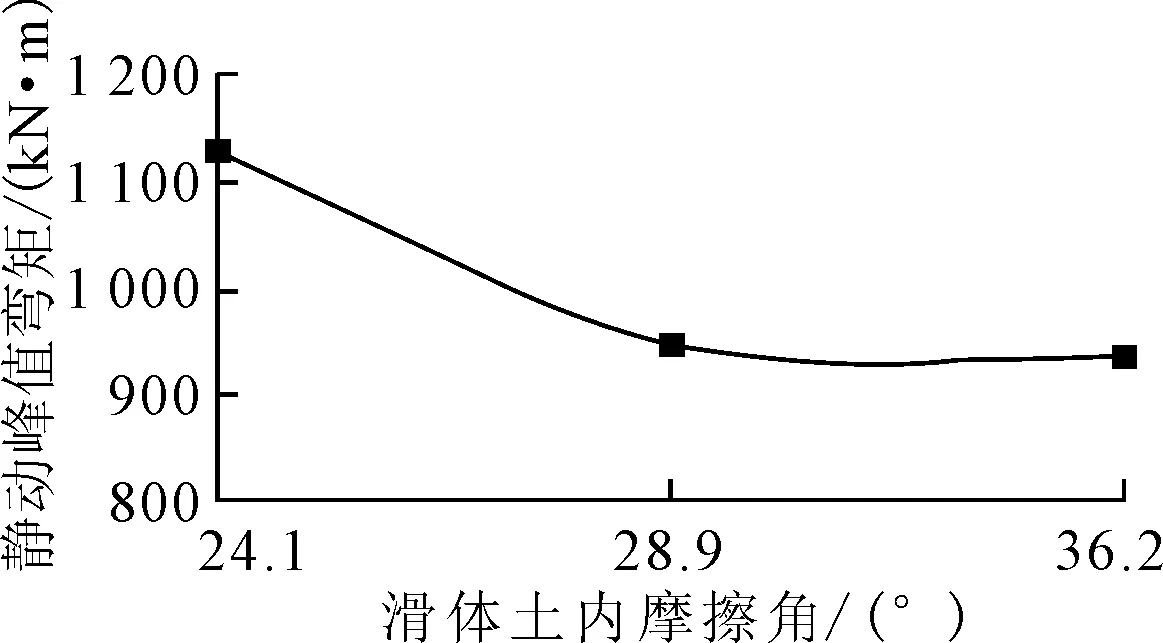
图18 静动峰值弯矩与滑体土 内摩擦角的关系

图19 桩身最大剪应力与滑体土 内摩擦角的关系

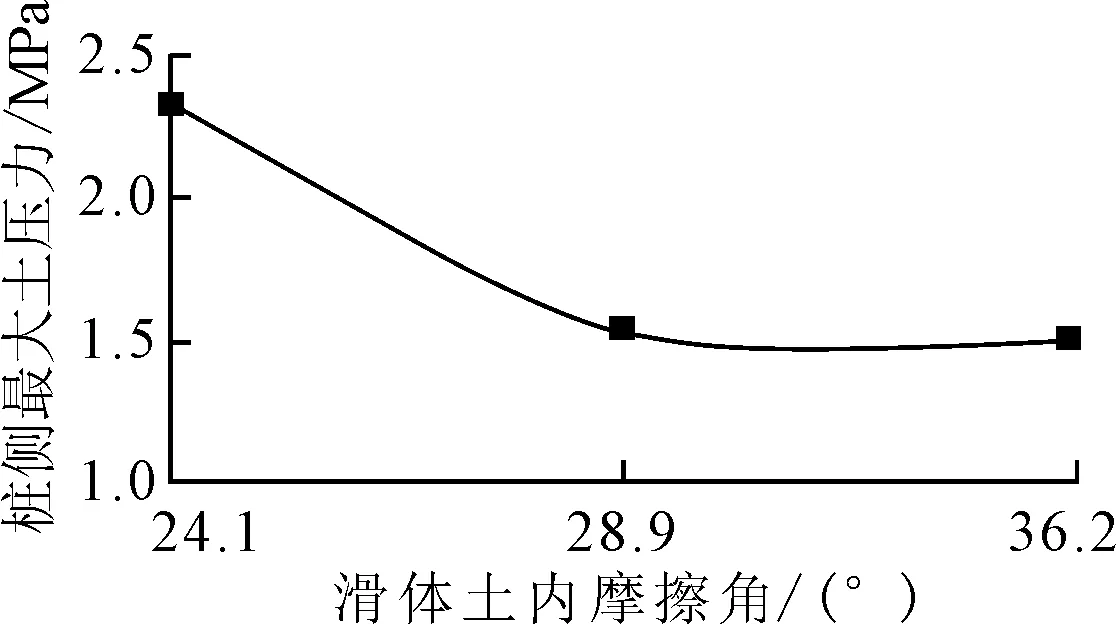
图20 桩侧最大土压力与滑体土 内摩擦角的关系

由图18～20可知，滑体土内摩擦角由24.1°增加至36.2°时，边坡稳定性增强，在地震力作用下的静动峰值弯矩、桩身最大剪力，以及桩侧最大土压力均在减小，其中滑体土内摩擦角由24.1°增至28.9°阶段曲线斜率较大，减小速度最快，其后趋向平缓.

3 结 论

1) 在动力作用下，桩嵌入基岩的锚固深度增大，桩身内力并不会一直增加.当桩的锚固长度小于等于H/2时，静动峰值弯矩，桩身最大剪力和桩侧最大土压力会随滑桩锚固深度增加而增加，而当锚固长度大于H/2时，这3种力学效应均增长减缓，之后开始缓慢减小.

2) 当门式双排桩的桩排距在一定范围内增大时，桩身最大剪力增大，而静动峰值弯矩与桩侧最大土压力则减小，此趋势表明此时抗滑桩加固效果在减弱.

3) 当门式双排桩间距为4倍方形桩截面宽度时，桩间的土拱效应最为显著，此时门型抗滑桩加固边坡和抵抗动力失稳的效果最好.而间距过大时，土拱效应不再明显；间距减小时，虽然整体动力加固效果更好了，但是由于桩根数增加，分配在单根抗滑桩上的滑坡力减小，且不够经济.

4) 滑体土及滑带粘聚力c和内摩擦角φ逐渐增大时，边坡稳定性提高，动力作用下静动峰值弯矩、桩身最大剪力及桩侧最大土压力都在减小，其中在滑体土粘聚力和内摩擦角的增大初期阶段，静动峰值弯矩与桩侧最大土压力减小速度快，而后趋于平缓.

[1]衣伟.考虑桩土相互作用高桩码头单桩地震反[M].港口工程,1997.

[2]MAHESHWARI B K, TRUMAN Z, NAGGAR M E, et al. Three-dimensional nonlinear analysis forseismic soil-pile-structure interaction[J]. Soil Dynamics and Earthquake Engineering,2004,24(4):343-356.

[3] TAKEWAKI I，KISHIDA A. Efficient analysis of pile-group effect on seismic stiffness and strength designof buildings[J]. Soil Dynamics and Earthquake Engineering，2005，25(5)：355-367.

[4]年廷凯，栾茂田.郑德凤考虑边坡内孔隙水压力效应的抗滑桩简化分析方法[J].岩土力学，2008(4)：1067-1071.

[5]汪鹏程,朱大勇,许群.强震作用下加固边坡的动力响应及不同加固方式的比较研究[J].合肥工业大学学报(自然科学版),2009,32(10)：1501-1504.

[6]张建经，刘强.抗滑桩水平地震作用修正系数分析—汶川地震典型抗滑桩破坏工点分析[J].土木工程学报,2012,45(增刊2)：89-92.

[7]李明康.加固边坡的双排抗滑桩合理排距的分析[D].成都：西南交通大学，2013.

[8]杨雪强，凌平平，向胜华.基于系列Drucker-Prager破坏准则评述土坡的稳定性[J].岩土力学，2009，30(4)：865-870.

[9]廖雄华，周健，张克绪，等.广义位移法在土-结构相互作用问题分析中的应用[J].岩土工程学报，2001，23(6)：672-676.

[10]马玉宏，谢礼立，赵桂峰.抗震设防烈度的决策分析方法研究[J].世界地震工程，2007，23(1)：86-90.

[11]陈清军，刘拓.地震波反演两种计算方法比较与频率截断问题的探讨[J].力学季刊，2010，31(3)：388-394.

[12]宋静.基于完整锚杆系统动力响应的围岩质量识别研究[D].重庆：重庆大学，2005.

Parameters Sensitivity Analysis of Slope with Double-rows Piles Under Bilateral Seismic Actions

DONG Bichang FU Shaoqing ZHANG Zhe

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)

The simulation model of slope with portal frame anti-slide piles is established with the finite element software Ansys in this paper. The force conditions under bilateral earthquake actions are studied through changing the model’s parameters such as depth of pile underground, pile row distance, pile space and shear strength parameters of soil. The results show that the static and dynamic peak bending moment, maximum shear stress of pile and maximum soil pressure on pile sides will increase with the increasing of anti-slide pile’s anchorage depth when the anti-slide pile’s anchorage depth is less than or equal toH/2, and these three mechanical effects will all increase slowly and then gradually decrease when the anti-slide pile’s anchorage depth is more thanH/2 under dynamic action. Besides, the static and dynamic peak bending moment and soil pressure on pile sides will reach the maximum when the row distance of portal frame anti-slide piles is 5.5m, and later these two mechanical effects will decrease with the increasing of the pile row distance. The soil arching effect between piles will be most significant when the pile space is four times the width of pile section. Also slope stability will increase when the cohesionc(25 kPa) and internal friction angleφ(24.1°) of soil slide body and slide zone gradually go up, and the decrease extent of static and dynamic peak bending moment, maximum shear stress of pile and maximum soil pressure on pile reaches the maximum when the values of c and φ are up to 1.2 times, and then it tends to be gentle.

bilateral seismic actions; slope with portal frame double-rows piles; parameters sensitivity analysis; FEM

2016-12-02

*中央高校基本科研业务费项目资助(2016-YS-021)

U416

10.3963/j.issn.2095-3844.2017.01.004

董必昌(1974—)：男，博士，副教授，主要研究领域为道路与桥梁工程