目标定位系统中图像失真的自动校正

谢文慧，曾培峰

(东华大学 计算机科学与技术学院，上海 201620)

目标定位系统中图像失真的自动校正

谢文慧，曾培峰

(东华大学 计算机科学与技术学院，上海 201620)

文章讨论了目标定位系统中失真图像自动校正的方法，并保证目标定位的精确性。在球面投影模型的基础上，以保持直线特性为约束，实现了广角镜头图像的自动校正。建立几何校正模型，采用分块迭代校正的方法，消除了不确定性误差的影响，可将失真图像中的目标精确定位到真实场景中。

目标定位；广角镜头；图像失真校正

0 引言

目标定位技术作为计算机视觉领域的热门研究方向，近年来受到科研人员的广泛关注。智能视频监控、移动机器人以及智能交通等新兴科学技术都与目标定位技术息息相关。然而，由于镜头特性的内在因素以及角度光线等外界因素，图像难免会出现失真的情况，图像失真的自动校正是实现目标定位的一个难点。

图像失真包括非线性失真和线性失真。非线性失真由镜头特性引起，具体表现为直线弯曲变形为弧线[1]。线性失真主要由拍摄角度引起，具体表现为垂直和水平线发生倾斜[2]。

基于镜头成像原理建立校正模型是非线性失真校正的基本方法，目前已有的非线性失真校正模型主要包括多项式畸变模型、对数畸变模型、球面投影模型和柱面投影模型等[3]。但校正模型的通用性不高，不能满足大多数失真图像的校正要求。PRESCOTT B和MCLEAN G F提出可以从单幅图像中提取信息[4]，并依据直线的线性特征进行校正。KEDZIERSKI M等人提出了依据差分几何和弧线曲率的校正方法[5]。这类基于图像内容的校正方法[6]校正效果更优，但计算量也更大。

线性失真校正分为2D校正和3D校正，GALLAGHER A C提出了2D平面内的自动旋转校正方法[7]，LEE H等人提出了基于人类感知学习的3D校正方法[8]。2D校正速度快但忽略了空间信息，3D校正算法较为复杂，两者各有利弊。CARROLL等人提出了基于网格的非线性优化方法[9]，其通过最小化直线失真程度和保持局部形状特征来优化校正效果，不过其需要与用户交互，不能实现自动校正优化。

本文根据目标定位精准性与实时性的要求，选取了合适的校正算法并加以改进，实现了失真图像的自动校正。此外，针对忽略图像视觉效果的应用场景，本文提出了分块迭代校正的方法。该方法最大程度地消除了各种不确定性误差[10]，实现了目标从失真图像到真实场景的精确定位。

1 系统介绍

本系统分为两部分：实时目标定位模块和离线校正模块，系统结构示意图如图1所示。

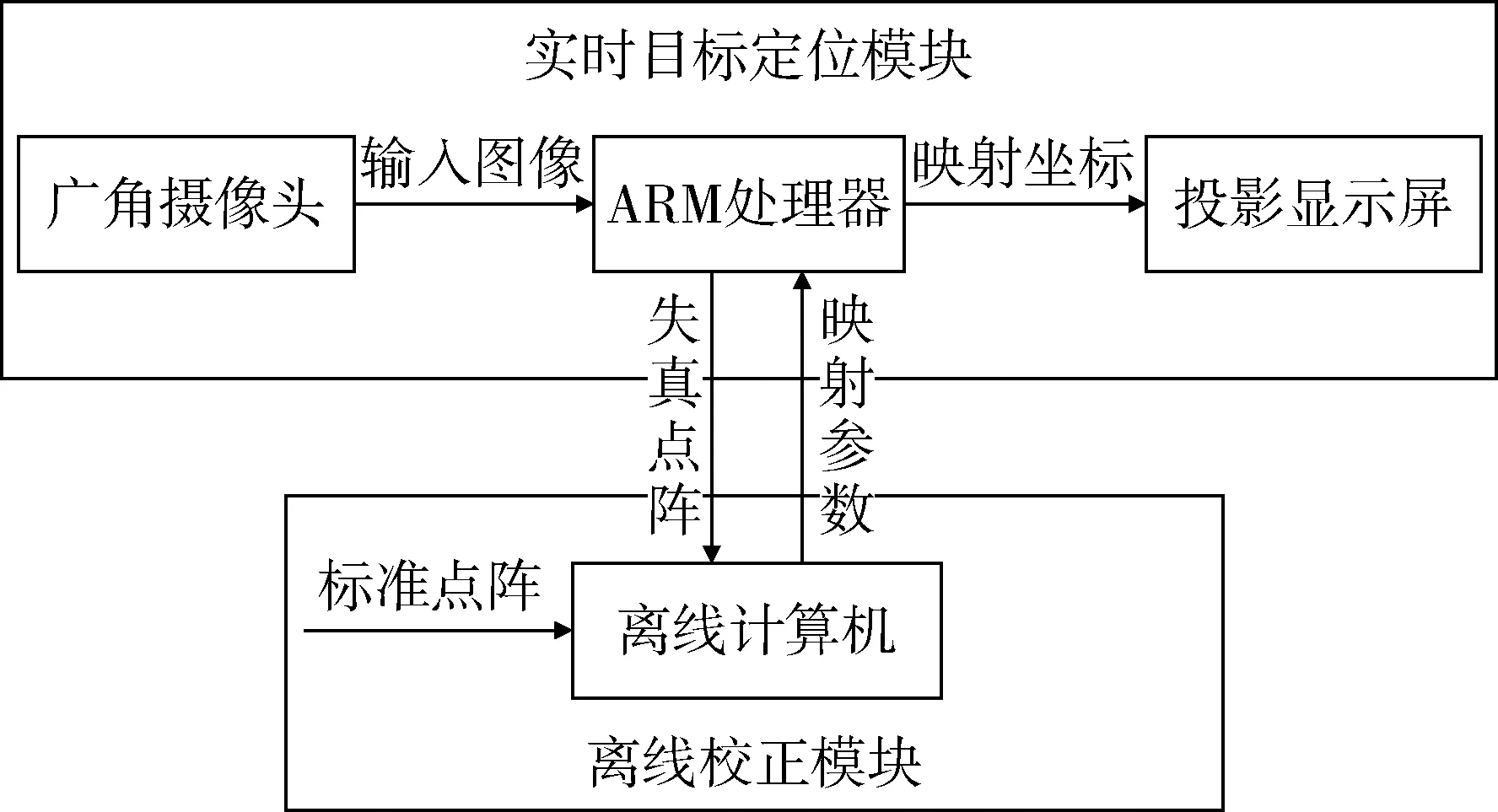
图1 系统结构示意图

目标定位的具体流程为：广角镜头采集输入图像，ARM处理器从输入图像中提取目标，根据映射参数进行坐标映射，最终标记出目标在真实场景中的位置，并显示到投影显示屏上。因为校正算法计算量很大，包含上千次的浮点数乘除法运算，而本系统使用的是Cortex-M3低功耗处理器，执行该算法会耗费大量时间，因此分离出校正模块来计算映射参数。

本系统的应用场景为军事模拟对战，对战场地面积较大，为了能够拍摄场地全景，选用了视角较大的广角镜头。输入图像为广角镜头拍摄的2×6幅1 024×768像素的静态照片。由于使用了广角镜头且摄像头与拍摄平面存在夹角，因此图像同时存在非线性失真和线性失真。

为了校正失真图像，并优化校正效果，本系统在对战场地中标记了9×7的标准矩形点阵，将场地等分成48个方形区域。经广角镜头拍摄后，该点阵会产生畸变，得到一个失真点阵，如图2所示。标准点阵与失真点阵的坐标数据作为离线校正模块的输入，用来计算实时定位模块所需的映射参数。

图2 标准点阵(圆圈)与失真点阵(星状点)

2 广角镜头失真校正

图3 广角镜头成像示意图

广角镜头的焦距短于标准镜头，因为光线的折射规律，拥有较大的视角。假设广角镜头的视角为V1OV2，拍摄方向沿Z轴，其成像原理如图3所示。对于空间中的一点Po，连接Po与球心O交球面于点Ps，Ps在X-Y平面上的投影点Pd即为Po的像点。

Po(xo,yo,zo)与Pd(xd,yd)的坐标关系如下：

(1)

将Po投影到X-Y平面上并转换为极坐标(r表示点到球心O的距离，θ表示点和球心连线与X轴的夹角)可得：

(2)

(3)

其中，R为球体的半径，D=zo为真实平面到像平面的距离。因为θo与θd相等，只需确定ro与rd的函数关系式(2)，即可实现失真图像的校正。

在镜头参数R未知的情况下，无法直接应用式(2)进行计算。本文利用标准点阵与失真点阵的坐标数据，采用多项式逼近的方法，拟合出等效于式(2)的函数关系ro=f(rd)。函数形式如下：

f(r)=k0+k1r+k2r2+k3r3+k4r4

(4)

其中，k0为平移分量，k1为线性失真参数，k2～k4为非线性失真参数。测试实验表明，4阶多项式的校正效果与3阶相比有很大提升，而更高阶较4阶的提升程度并不明显。本文最终选择4阶多项式进行拟合。

3 直线特性约束

直线是图像中非常明显的一种信息，保持直线特性可作为图像失真校正的约束条件。假设(x1,y1)、(x2,y2)和(x3,y3)为失真图像中3个像素点校正后的坐标，如果这3点在一条直线上，应该满足：

(5)

其中dij表示(xi,yi)和(xj,yj)两点间的距离。

在校正后的图像中，选取原本应在同一条直线l上的N个离散点，根据式(5)可以推导出l的直线能量函数：

(6)

其中Xn表示平面中点的笛卡尔坐标(xn,yn)。图像中所有直线的能量函数总和∑El可用来衡量校正效果，∑El越小则校正效果越佳。

4 线性失真校正

线性失真校正是对失真图像进行仿射变换，使倾斜的直线重新恢复垂直或水平。一些复杂的仿射变换模型可能会有较好的校正效果，但是需要从图像中获取大量信息，并且计算过程复杂。而本系统的目标是坐标映射的精确度和运算速度，对图像内容的校正效果(如清晰度等)没有要求。因此，本文忽略图像的颜色、深度等信息，只利用图像中目标点的坐标信息来建立仿射变换模型。

对于失真图像I和原始图像I′，存在映射关系H，I上的任意一点(x,y)都可通过H映射到I′上的一点(x′,y′)，即：(x′,y′)=H·(x,y)。仿射变换模型的建立就是确定失真图像与原始图像之间的映射关系H，本文选取的映射方程如下：

(7)

(8)

上式中有8个未知数，选取失真图像与原始图像中4组对应点，建立并求解线性方程组，即可求出映射关系H。

5 分块迭代校正

对于面积较大的图像，不同区域的失真程度也不同，只用一个校正模型对整幅图像进行校正，无法保证校正效果，对图像进行分块校正可以优化校正效果。并且邻近的分块之间是相互关联、相互约束的，利用这种约束关系可以减少误差。

针对本文的校正对象(9×7的点阵)，依据点阵的分布，将图像划分为48块。每4个点组成一个四边形区域，为一个分块S，如图4所示。由上文可知，4组对应点可确定一个映射关系H，因此每一个分块Si都可求解出一个映射关系Hi。对失真图像中任意一点，先确定其在图像中属于哪一个分块，然后利用该分块对应的映射关系计算出该点在原始图像中的坐标。

图4 点阵分块示意图

6 实验结果

应用式(4)对失真点阵进行非线性失真校正后的结果如图5所示。可以看出，原本呈曲线分布的点阵已基本恢复线性。但此时的点阵并不能完全满足直线特性约束。继续对点阵进行分块迭代校正，最终得到的点阵如图6所示。

图5 非线性失真校正前后对比图

图6 迭代校正后的点阵

图7为迭代校正时，图像中所有直线的能量函数总和∑El的变化情况。迭代15次之后，∑El已减小90%，迭代35次之后，∑El已趋向于0。

图7 迭代过程中∑El的变化

根据图6所示点阵与标准点阵的坐标信息，计算出所有图像块的映射参数Hi(i=1,2,…,48)，输入实时目标定位模块，最终坐标映射的计算结果如表1所示。

表1 坐标映射计算结果

表1结果表明，本系统计算出的映射坐标和真实场景中的坐标基本吻合。在1 024×768的图像中，误差控制在一个像素范围内。

7 结论

针对注重精度与速度而不要求视觉效果的应用场合，本文提出了有效校正非线性失真和线性失真，并可消除镜头缺陷及人工失误所产生误差的方法，可实现失真图像中的目标在真实场景中的精确定位。

[1] Wei Jin, Li Chenfeng, Hu Shimin, et al. Fisheye video correction[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(10): 1771-1783.

[2] WILIEM P, SIMON C, CHO S, et al. Fast and robust perspective rectification of document images on a smartphone[C]. IEEE Conference on Computer Vision and Pattern Recognition Workshops. IEEE Computer Society, 2014: 197-198.

[3] HAN S B, KIM J H, MYUNG H. Landmark-based particle localization algorithm for mobile robots with a fish-eye vision system[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(6): 1745-1756.

[4] PRESCOTT B, MOLEAN G F. Line-based correction of radial lens distortion[J]. Graphical Models and Image Processing, 1997, 59(1): 39-47.

[5] KEDZIERSKI M, FRYSKOWSKA A. Precise method of fisheye lens calibration[C]. Proceedings of the ISPRS-Congress, Beijing, China. 2008: 765-768.

[6] Zhang Mi, Yao Jian, Xia Menghan, et al. Line-based multi-label energy optimization for fisheye image rectification and calibration[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, 2015: 4137-4145.

[7] GALLAGHER A C.Using vanishing points to correct camera rotation in images[C]. The 2nd Canadian Conference on Computer and Robot Vision (CRV'05), IEEE, 2005: 460-467.

[8] LEE H, SHECHTMAN E, WANG J, et al. Automatic upright adjustment of photographs with robust camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(5): 833-844.

[9] CARROLL R, AGRAWALA M, AGARWALA A. Optimizing content-preserving projections for wide-angle images[J]. ACM Transactions on Graphics-TOG, 2009, 28(3): 43.

[10] HOU W, DING M, QIN N, et al. Digital deformation model for fisheye image rectification[J]. Optics express, 2012, 20(20): 22252-22261.

Automatic image correction in target location system

Xie Wenhui, Zeng Peifeng

(College of Computer Science and Technology, Donghua University, Shanghai 201620, China)

An automatic image correction method for target location system is discussed in this paper. Based on spherical projection model, considering the linear maintain constraint, wide-angle lens image can be automatically corrected. The geometric correction model is established, and a method of block iterative correction is adopted to eliminate the influence of any uncertainty error. The target in the distorted image can be accurately located in the real scenario.

target location; wide-angle lens; image distortion correction

TP751

A

10.19358/j.issn.1674- 7720.2017.03.013

谢文慧，曾培峰.目标定位系统中图像失真的自动校正[J].微型机与应用，2017,36(3)：42-44，48.

2016-10-11)

谢文慧(1994-)，女，硕士研究生，主要研究方向：图像处理与模式识别。

曾培峰(1964-)，男，工学博士，教授，主要研究方向：图像处理与模式识别、算法研究、嵌入式系统、计算机网络与通信。