动力电池模拟器的设计

马红雷,司文旭,郑 玉

(重庆理工大学 电气与电子工程学院，重庆 400054)

动力电池模拟器的设计

马红雷,司文旭,郑 玉

(重庆理工大学 电气与电子工程学院，重庆 400054)

电动汽车及相关设备的生产、测试和研发过程中，需要用到动力电池；当使用动力电池作为测试电源时，存在充电时间长、效率低、污染环境且成本高等问题。选择合适的电池模型，使用某一种电池作为测试的试验平台，通过测试的实验数据来辨识电池参数。使用正态分布和卡方分布的方法，完成由单一单体电池到成千上万个单体电池的模拟。最后，建立了Simulink仿真模型，仿真结果表明该设计能够模拟多元化电池。在使用电池模拟器作为驱动电机的测试电源时，省去了动力电池充电的过程，提高了测试电机的测试效率，节约了成本，减少了环境污染。

参数辨识；Simulink仿真模型；多元化模拟

0 引言

随着燃油汽车造成的环境污染越来越严重和世界能源的日益枯竭，纯电动汽车的研究开始受到广泛的关注和重视。纯电动汽车关键动力源是动力锂离子电池，动力锂离子电池具有能力密度高、自放电率低和循环周期长等优势。如果使用动力电池作为测试电池的驱动电源则有如下缺陷[1]：(1) 由于动力电池的容量大，驱动电机测试完成之后，需要给动力电池充电，其充电过程需要很长的时间，影响了测试周期的连续性和完整性；(2)由于动力电池制造工艺上的特殊性，反复地充电和放电使电池的使用寿命缩短并且内阻增大，影响了测试驱动电机的试验条件；(3)如果进行特殊试验，如进行紧急制动测试，实验过程中产生的尖峰电流会使电池特性恶化，使用寿命大大缩短，影响了测试数据的准确性和可靠性。通过上述几点可以分析出动力电池直接作为测试电源是不合理的。本文设计出一种电池模拟器，能够模拟电池的充电和放电特性。使用电池模拟器作为驱动电机的测试电源时，省去了动力电池充电的过程，提高了测试电机的测试效率，节约了成本，减少了环境污染。

1 电池的荷电状态

由电池的荷电状态(SOC)可以估算出电池的剩余可用容量,因此可以根据电池剩余容量占电池容量百分比对其进行表示，把电池不能吸收能量这一状态定义为100%，把电池不能放出能量这一状态定义为0%。一般电池SOC表达式如下[2-4]：

SOC=SOC0-∫(ibatt/C)dt

(1)

式中，SOC0是动力锂离子电池的荷电状态的初始电荷，C为动力锂离子电池的实际容量，ibatt是电池负载的电流，SOC是当前的荷电状态。

1.1 单体电池放电

锂离子电池在不同温度、充放电倍率、循环次数和电池的老化程度下，放电电压曲线是不同的，为了简化研究电池的难易程度，本文选取环境温度为参考温度，选取的电池为18650锂离子电池2 900 mAh，放电倍率为0.4 C。电池测试平台选用美尔诺M9712系列直流电子直流负载，它具有恒流、恒压、恒功率和恒阻操作模式，配合PC配套软件使用，上位机软件可以设置为电池放电功能，可以设置电池放电周期、电池安全电压和计算电池放电容量等功能。

在环境温度下，放电倍率为0.4 C恒流放电条件下，单体电池电压与放电时间的关系曲线如图1所示。

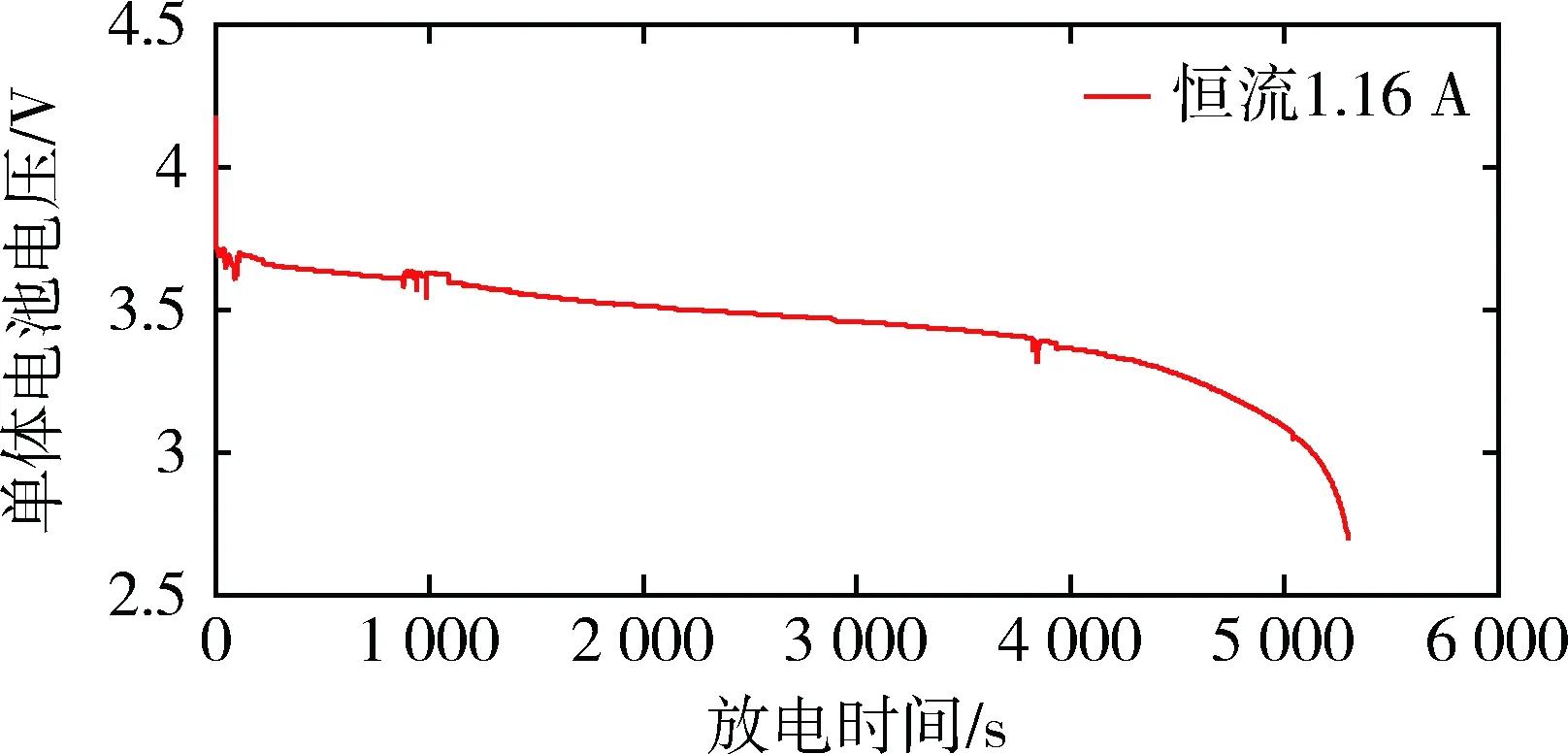
图1 电池电压与放电时间的关系曲线

从图1中可以看出放电过程分为3个阶段，第一个阶段为陡峰期，电池电压瞬间从4.2 V下降到3.8 V左右，紧接着进入平台期，在此期间电池电压有下降的趋势，在整个放电过程中占了将近80%以上的时间，当电池剩余容量不到10%时，电池电压再次出现陡峰期，电池放电时间不到5 min，电池电压下降到2.7 V，放电截止[5]。

1.2 动力锂离子电池与开路电压之间的关系

在环境温度下，对锂离子电池以0.4 C恒流放电试验，计算出实际放出的容量，实验中把实际放出的电量分成10等份，每一等份释放完就视为SOC下降了10%，每当SOC下降了10%就静止一定的时间，然后测量电池的电压，测量的电池电压就视为电池的开路电压，如图2和图3所示[6-7]。

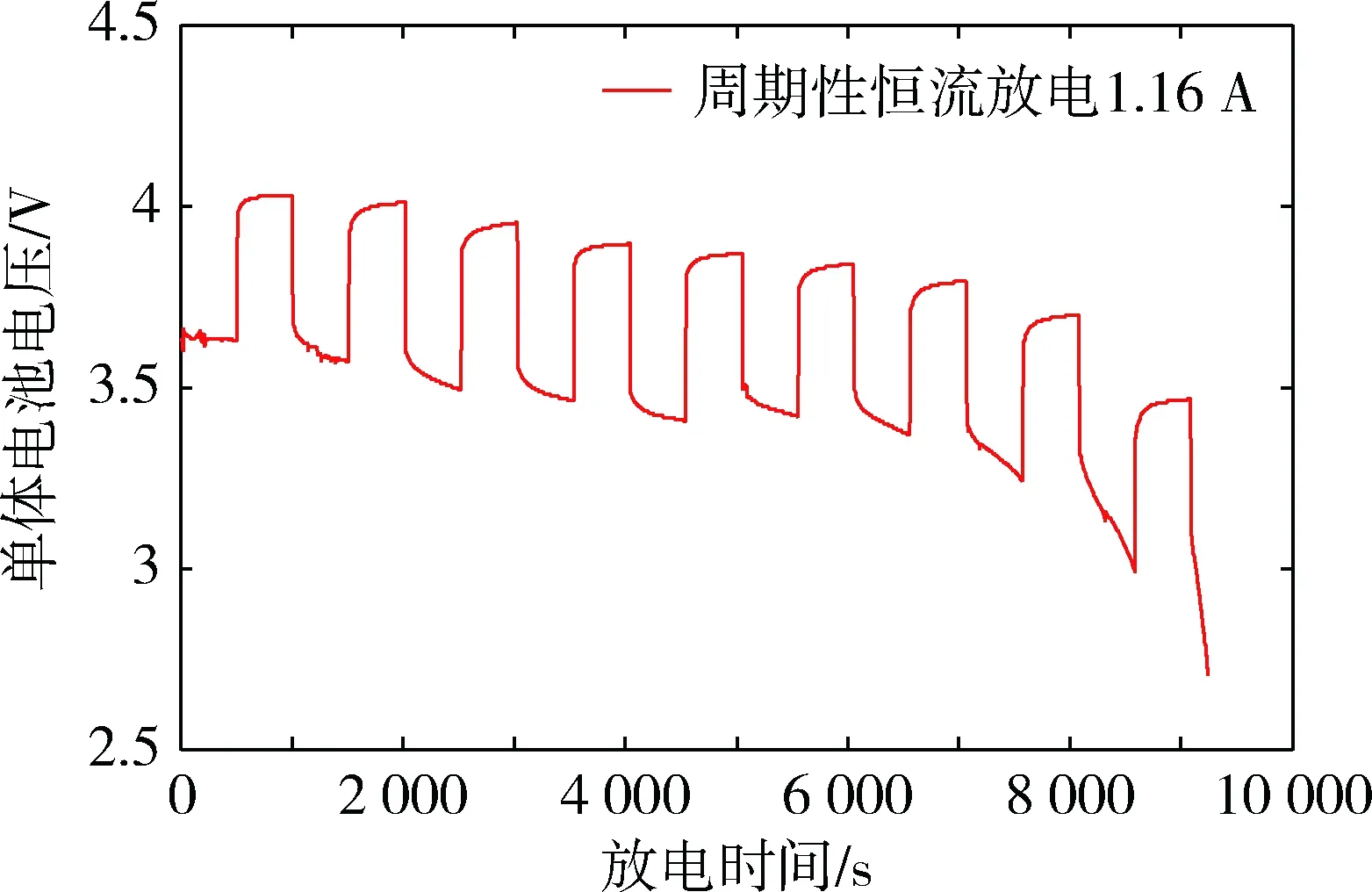
图2 0.4 C周期恒流放电电压与时间曲线

图3 周期放电0.4 C放电电流曲线

从图2、图3中可以看出，每个阶段电池电流变为零时，电池电压缓慢上升，总体趋势开路电压是下降的，从测试的实验数据中可以得出OCV与SOC之间的关系如表1所示。

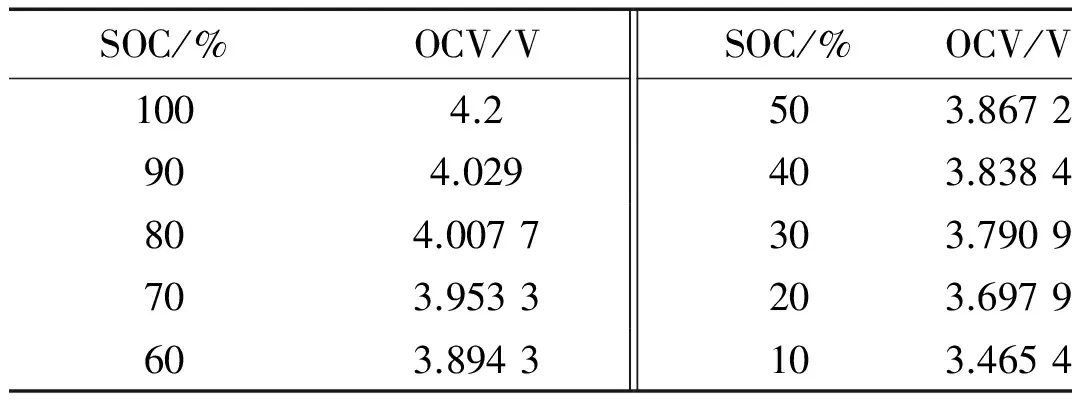
表1 OCV与SOC之间的关系

通过表1中的数据可以拟合出电池SOC的值与开路电压OCV关系曲线图。其相应关系可以用一条曲线来拟合表示，如图4所示。

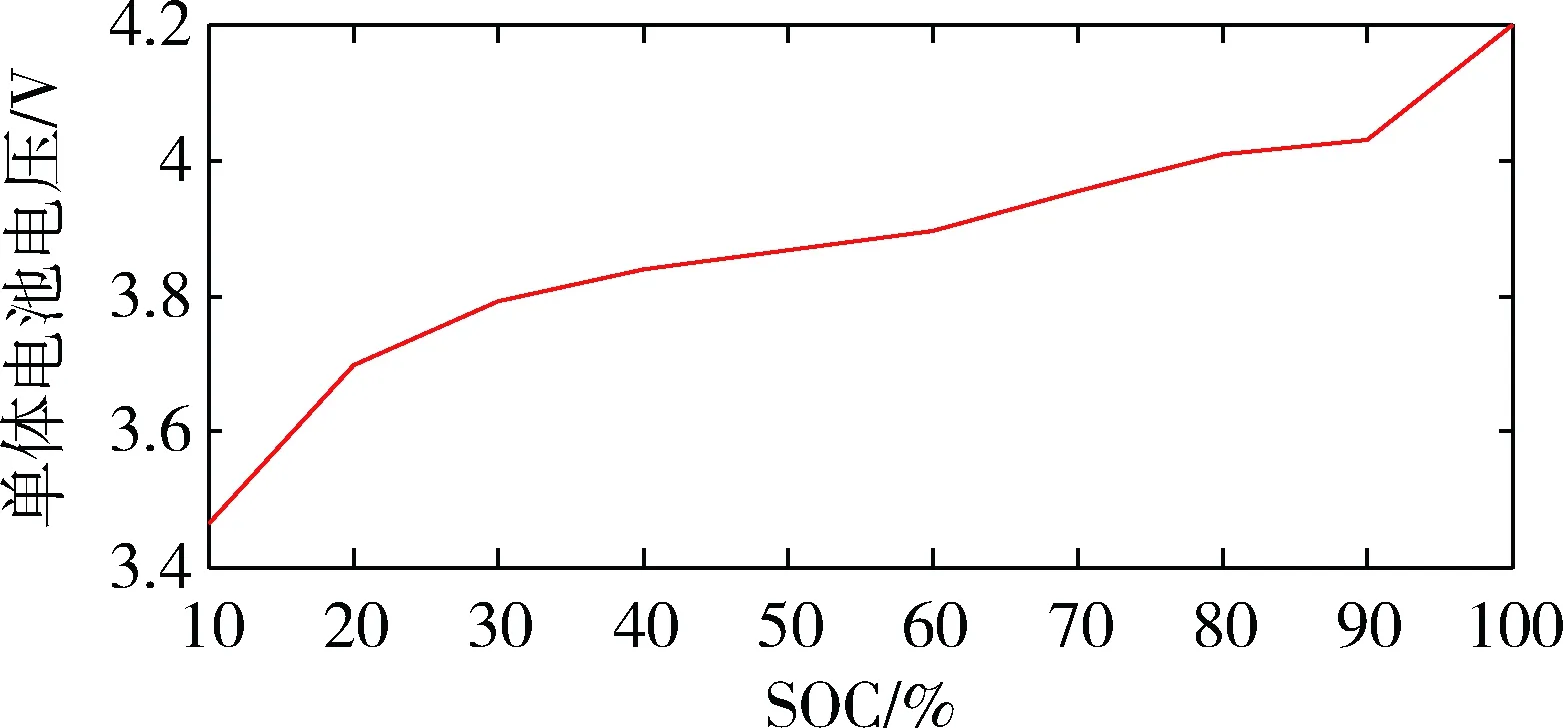
图4 OCV与SOC关系曲线

2 锂离子电池参数辨识

从图5中可以看出，当电池中的电流突然变为零时，电池电压将产生突变，将电池电压上升部分分为4个阶段，第一个阶段为B～C，电池电压变化较大，这是由于电池内阻欧姆电压消失造成的；第二个阶段C～D电池电压缓慢上升，持续时间较短，是由于电池极化短期消失的过程；第三个阶段D～E，电池电压缓慢上升，持续时间较长，是电池极化电压长期消失的过程；最后一个阶段E点之后电池电压将不再上升，这时的电池电压等于电池的开路电压。

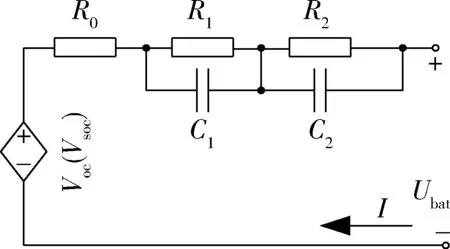
图6 二阶等效电路模型

图5 电池的动态特性

通过分析锂离子电池电压瞬态响应，同时考虑了各种外界因素，本文采用的电池等效电路模型如图6所示[3]。

当电池放电时，电流流动的方向如图6所示，此时电流方向为正，根据电路原理分析可以计算出电压与电流之间的关系为：

Ubat=Voc(SOC)-R0I-Uc1-Uc2

(2)

(3)

(4)

从图2周期恒流放电实验中可以看出，当电池放电时，电池电压输出曲线呈现指数下降趋势，电流突然变为零时，电池的输出有一个瞬变电压，紧接着按照指数形式继续上升。这种趋势变化的主要原因有：当电池放电时，极化电容C1和C2进行充电，形成RC极化电压V1和V2，当电池中的电流变为零时即电池静止状态时，极化电容两端的电压通过并联电阻放电，电压呈现指数下降[8]。图5是图2的局部放大图，图中A点是电池放电开始时刻，B点是放电停止时刻，A→B是放电区域，放电时间足够长，E点是静止停止时刻，B→E是静止趋势，静止时间足够长，其中E点中的电压为Voc(SOC)。

在A→B区域中，RC网络为零状态响应，其输出电压为：

(5)

假设图5中tA～tB期间为放电时刻，tB～tE期间为静止时刻，其中tA为放电开始时刻，tB为放电停止时刻，则A→B区域中任意时刻t(以tA为原点)输出的电池电压为:

Ubat(t)=Uoc(SOC)-u1(t)-u2(t)-i(t)R

(6)

(7)

图5中，B点电流为零的瞬间，电池的电压瞬间抬高，这是由于电池的欧姆内阻引起的，从图6等效电路模型中可以得出内阻R0,则内阻R0可用下列公式计算得到：

(8)

同理可以推出C→E任意时刻电池的输出电压为：

Ubat(t) =Uoc(SOC)-u1(t)-u2(t)

(9)

方程进行系数替换：

在《雷雨》第二幕中，当周朴园听出鲁侍萍的无锡口音时，跟她聊起三十年前的无锡旧事时，有如下一段对白：“周朴园：哦，三十年前你在无锡？鲁侍萍：是的，三十多年前呢，那时候我记得我们还没有洋火呢。”这里，人称代词“我们”用得妙极！后一句本来完全可以说成“我记得那时候还没有洋火呢”，可是作者不避重复，且故意选用“我”与“我们”的错位，“我们”这一本应该包括听话人在内的人称实为鲁侍萍放出的试探气球，倘若周朴园心神警觉，早该听出其弦外之音，以揭开眼前这位妇人的身世之谜，显然在鲁侍萍的心头蒙上一层阴影。

Ubat=f-b1e-τ1t-b2e-τ1t

(10)

比较式(7)和式(9):

(11)

通过使用MATLABcftool工具箱利用最小二乘法拟合成曲线如图7所示。

图7 双指数拟合曲线

由式(10)～(11)及通过拟合曲线方程可以辨识出电池参数，具体参数如表2所示。

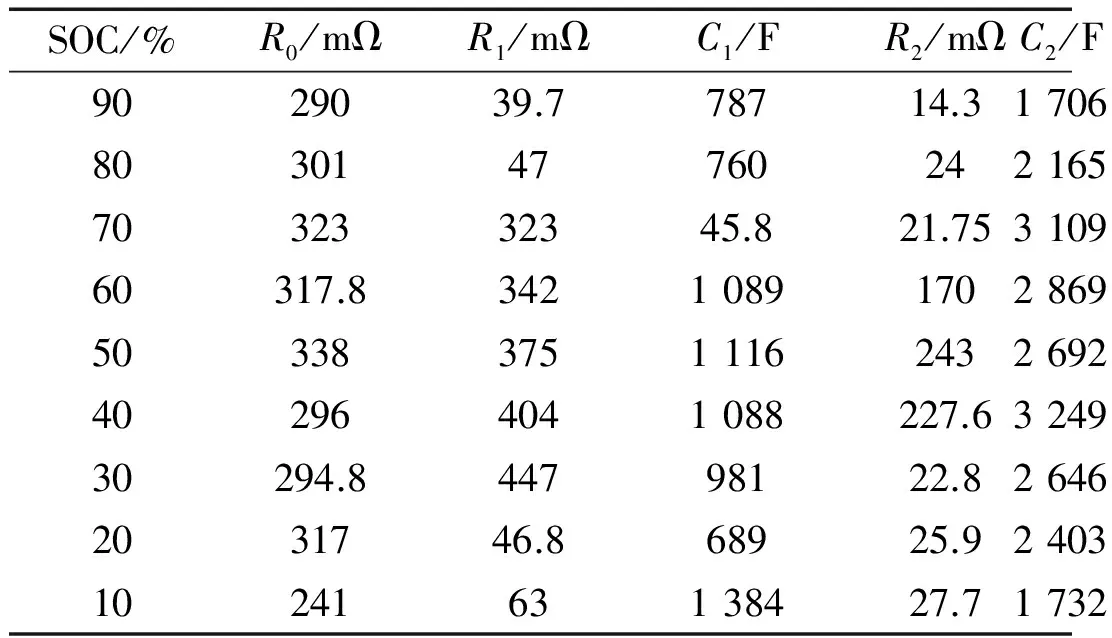
表2 二阶模型参数表

3 多元化电池模拟

(12)

每一个单体电池的状态初始值是不同的，常规意义上的电池模拟需要将电池模拟数量进行简单的求和，这样的模拟是不精确的。每一个单体电池都有对应的温度信号、电压信号、电流信号等，由传感器进行信号采集。通过每一个单体电池也要模拟出真实电池的运行特性,这样就会大大增加整个模型的运行时间。

进行硬件在环测试的电池模型必须具有多元电池能力。一个电池模拟器能够处理几十个单体电池，但是模型的数据需要对成千上万的单体电池进行模拟。这个模型需要有效地模拟多元化电池。

使用概率密度来对电池的参数进行仿真。它使用一个不同的矩阵来生成电池的不均衡，电池模型用于硬件在环对不同参数的单体电池验证。使用两个普通的概率分布：正态分布和卡方分布。正态分布如图8所示，卡方分布如图9所示，用于产生单体电池电容和给定SOC开路电压的函数。正态分布的特征是均值和标准偏差。

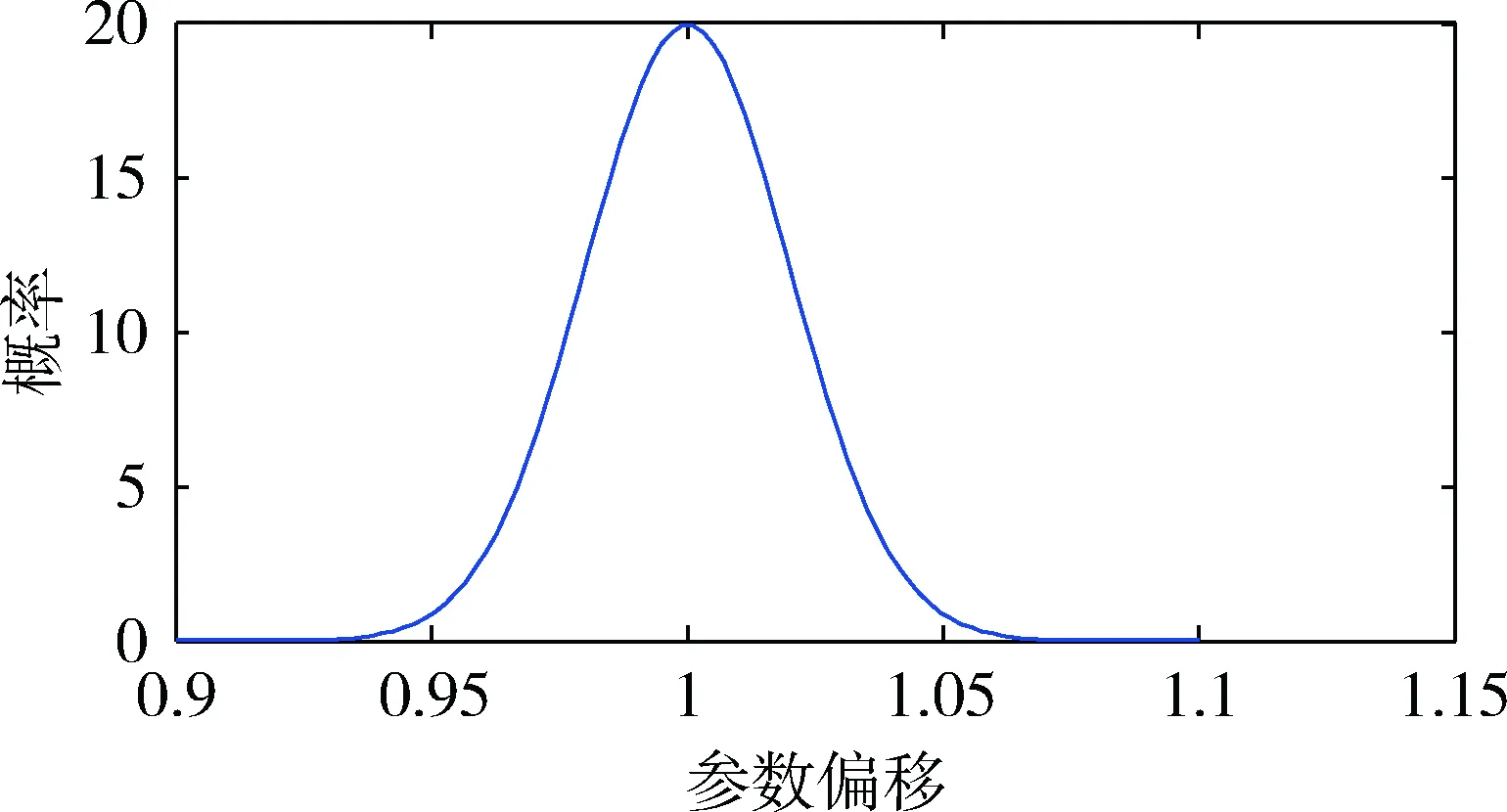
图8 正态分布

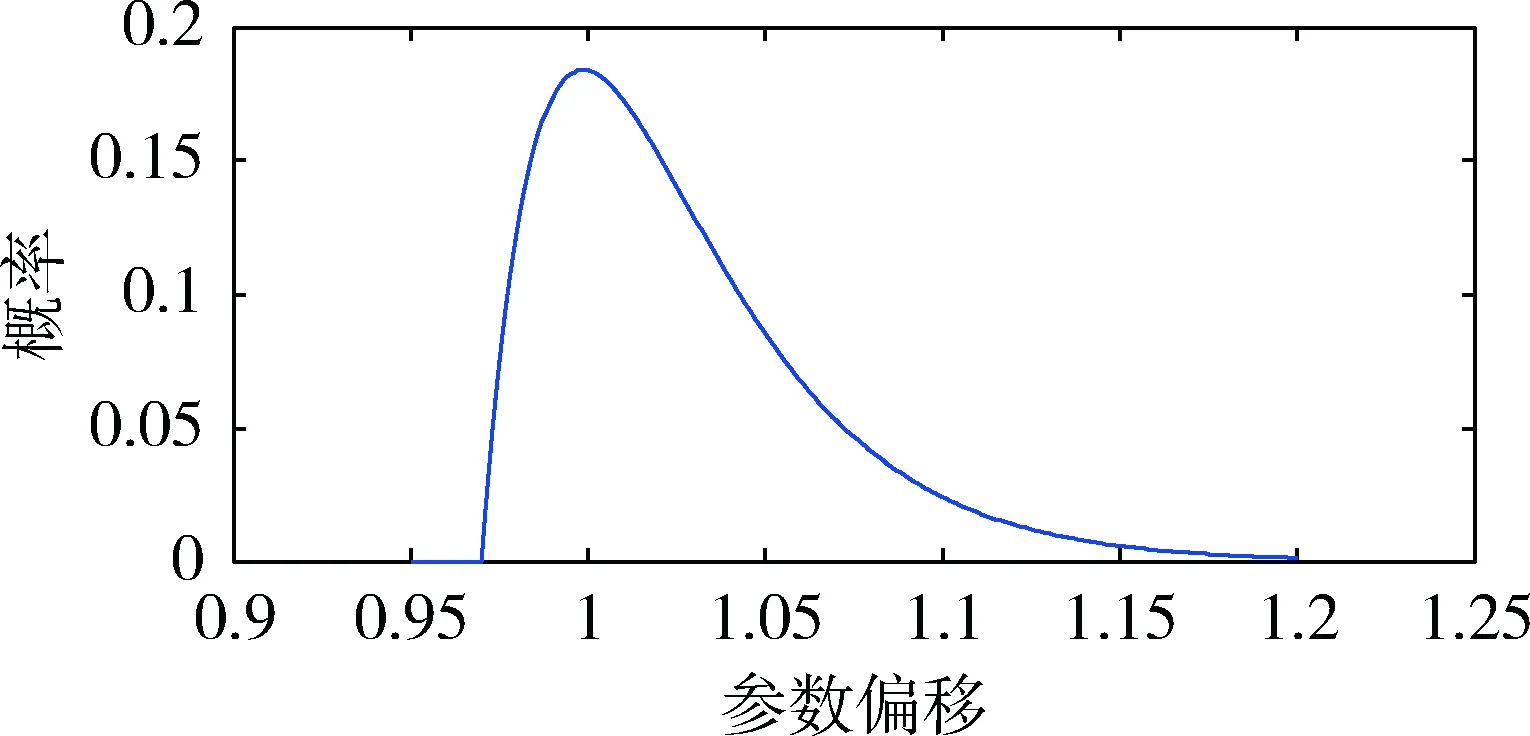
图9 卡方分布

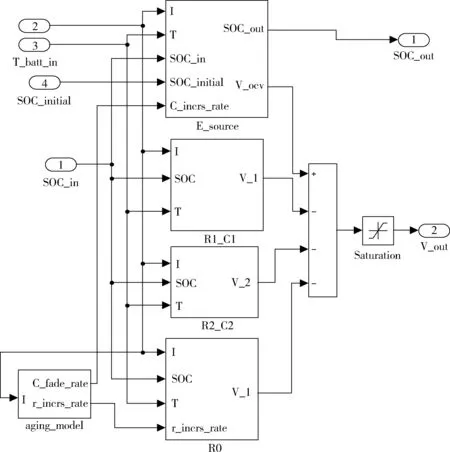
图11 电池二阶等效电路模型子模型

考虑到电池特性的偏差，这时每个电池的电流、内阻、初始SOC和电池容量的放大系数可以分别设置为：

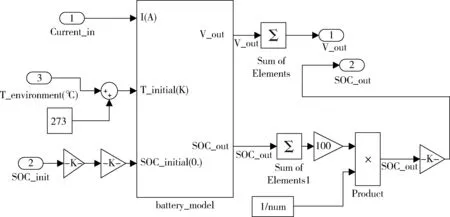
图10 电池等效模型

SOC_initial_scale=normrnd(1,0.02,num,1)

(13)

battery_current_scale=ones(num,1)

(14)

para_different=normrnd(1,0.02,num,1)

(15)

r_scale=chi2rnd(4,[num,1])/70+0.97

(16)

式中num表示电池的数目，这就将电池的输入转化为矩阵输入，每一个输入值都存在微小的差异。

电池等效模型包括电压源模型、二阶RC模型，如图10所示，而图11是图10子模型。

同一类型的电池都存在微小的差异，能够模拟几十个到上千个电池，使用正态分布和卡方分布参数差异化方法来模拟数量庞大的电池，图12是模拟40节电池的放电曲线。

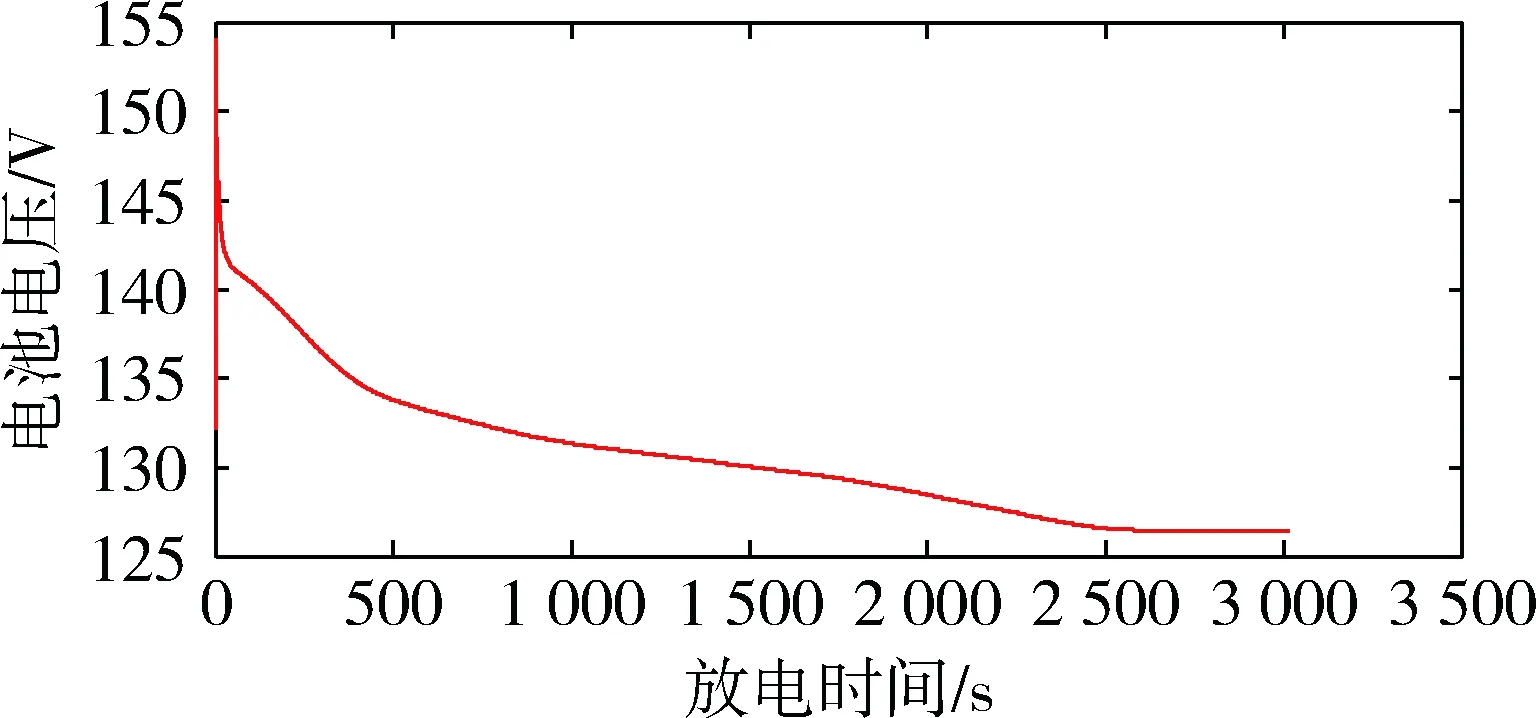
图12 模拟电池放电曲线

4 结论

本文通过查阅相关文献，选择了合适的电池模型结构，在不同放电倍率下辨识出了电池的参数，通过提出的这些参数建立了数学模型，最后通过Simulink仿真进行了验证。

使用正态分布和卡方分布，提出了电池参数的差异化，利用电池参数差异化对电池模拟数量求和，从而具有由单体电池到模拟多元化的能力。

[1] 王志强. 电动汽车动力锂离子电池模拟器的研究[D]. 重庆：重庆理工大学,2012.

[2] 邓涛,孙欢.锂离子电池新型SOC安时积分实时估算方法[J].重庆理工大学学报(自然科学版),2015,29(1):101-106.

[3] 卢杰祥.锂离子电池特性建模与SOC估算研[D].广州：华南理工大学,2012.

[4] 高安同,陈荣刚. 锂离子电池健康预测方法[J]. 重庆理工大学学报(自然科学版)，2014,28(2):102-105，110.

[5] TSANG K M, CHAN W L, WONG Y K, et al. Lithiumion battery models for computer simulation [C].2010 IEEE International Conference on Automation and Logistics,2010:98-100.

[6] 肖蕙蕙,王志强,李山,等.电动汽车动力锂离子电池建模与仿真研究[J].电源学报，2012(1):41-44.

[7] Zheng Minxin, Qi Bojin, Du Xiaowei.Dynamic model for characteristics of Li-ion battery on electric vehicle[C].4th IEEE Conference on Industrial Electronics and Application,2009:2867-2871.

[8] 文平.动力锂离子电池模拟器的研制[D].哈尔滨:哈尔滨工业大学,2013.

Design of power battery simulator

Ma Honglei, Si Wenxu, Zheng Yu

(Department of Electrical Engineering and Electronics, Chongqing University of Technology,Chongqing 400054,China)

In the process of producing, testing and researching for electric vehicles and related equipments, power batteries are needed. When the power battery is used as the test power,the charging time is long,the efficiency is low,the pollution for environment and the cost is higher.By choosing appropriate battery model,a kind of battery is selected as the platform,and the parameters of the battery are identified by the test data.Using the method of normal distribution and chi square distribution, the simulation of single cell battery is used to simulate thousands of single cell battery. Finally, the Simulink simulation model is established, and the simulation results show that the design can simulate a multiple battery. If the battery simulator is used as the testing power supply of the driving motor, the power battery charging process is omitted, the test efficiency of the test motor is improved, the cost is saved, and the environmental pollution is reduced.

parameter identification;Simulink simulation model;multiple simulation

TM912

A

10.19358/j.issn.1674- 7720.2017.03.003

马红雷，司文旭，郑玉.动力电池模拟的设计[J].微型机与应用，2017,36(3)：8-11，15.

2016-10-09)

马红雷(1988-)，男，硕士研究生，主要研究方向：电力电子与新能源技术。

司文旭(1990-)，男，硕士研究生，主要研究方向：电力电子与新能源技术。

郑玉(1991-)，男，硕士研究生，主要研究方向：电力设备故障在线检测。