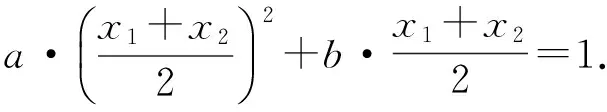函数与导数复习专题
●李金兴 (萧山中学 浙江杭州 311201) ●许兴铭 (萧山区教学研究室 浙江杭州 311201)
函数与导数复习专题
●李金兴 (萧山中学 浙江杭州 311201) ●许兴铭 (萧山区教学研究室 浙江杭州 311201)
函数部分高考内容包括函数的概念与表示、图像与性质、基本初等函数、函数应用、导数及应用等.解函数题需要能熟练应用数形结合、分类讨论、化归转化等思想方法,函数综合问题涉及方程、不等式等,抽象或构造函数模型解题也是能力立意的一类问题.
函数;导数;高考复习
1 知识内容
函数是描述客观世界变化规律的重要数学模型,贯穿了整个高中阶段的数学学习,历来是高考的重点内容之一,导数及其应用深化和提高了函数的学习与研究.2017年浙江省数学高考函数与导数内容包括:1)函数、映射的概念与函数的表示方法;2)函数性质(单调性、奇偶性、最值等);3)基本初等函数Ⅰ(指数函数、对数函数、幂函数);4)函数与方程之间的关系;5)函数的简单应用;6)导数的概念与几何意义;7)导数的运算(基本初等函数的导数公式和运算法则);8)利用导数求函数的单调性、极值、最值.
2 命题分析
从映射角度认识函数是高中数学的基本要求,但在具体情景中去识别函数表示仍有一定难度(如复合函数、抽象函数等).函数性质还包括周期性、图像的特性等,对函数图像与性质的研究不限于基本初等函数(如三角函数、四则运算后的函数等),导数在研究函数图像与性质时理应成为犀利的工具.函数的应用不仅是建立函数模型来研究生活情景中的问题,也往往与其他数学内容(如方程、不等式、数列、几何)综合起来.与前几年考试说明相比,“掌握连续函数在某个区间上存在零点的判定方法”是新的要求.
3 典例剖析
3.1 函数概念与表示
( )
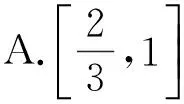

分析 没必要将复合函数y=f(f(x))和y=2f(x)分别分段表示出来,可通过换元来简化函数表示.先考虑方程f(t)=2t的定义域为t∈[1,+∞),从而易得答案选C.
例2 已知定义域为R的函数f(x)满足f[f(x)-x2+x]=f(x)-x2+x.
1)若f(2)=3,求f(1);又若f(0)=a,求f(a).
2)设有且只有1个实数x0使得f(x0)=x0,求f(x)的解析式.
分析 用赋值法尝试探究抽象函数.第1)小题,当f(2)=3时,令x=2即得f(1)=1,同理当f(0)=a时,f(a)=a.第2)小题由方程f(x)=x解的唯一性知f(x)-x2+x=x0,令x=x0,解得x0=0或x0=1,检验得x0=1,于是
f(x)=x2-x+1.
3.2 函数的图像
例3 下列关于函数f(x)=sinx+x图像的描述错误的是
( )
A.图像关于原点对称
B.图像对称中心有无数个
C.图像有平行于y轴的对称轴
D.图像与x轴只有1个交点

图1
分析 图像特征实质上是函数性质的直观显示.因为f(x)是R上单调递增的奇函数,所以选项A,D一定正确,选项C一定错误;选项B有较强的迷惑性,画出草图(如图1所示)可知选项B正确.值得一提的是,该函数图像尽管有无数多个对称中心,但它不是周期函数.
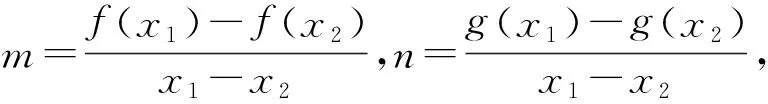
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中的真命题有______(写出所有真命题的序号).
分析m,n的几何意义是连接函数图像上2个点的直线斜率.因为f(x)是增函数,所以命题①显然正确,而命题②显然错误.而仅凭图像直观很难对命题③和命题④作明确的判断,需要将问题进行转化.
m=n等价于
f(x1)-f(x2)=g(x1)-g(x2),
即
f(x1)-g(x1)=f(x2)-g(x2).
令h(x)=f(x)-g(x)=2x-x2-ax,则
h′(x)=2xln2-2x-a,
而对于任意的a,函数h′(x)未必有零点,因此h(x)可能是单调函数,命题③可能不成立.
m=-n等价于
f(x1)+g(x1)=f(x2)+g(x2),
令h(x)=f(x)+g(x)=2x+x2+ax,则
h′(x)=2xln2+2x+a,
易知h(x)一定有极值点,因此命题④成立.故命题①和命题④是真命题.
3.3 函数性质
例5 定义在R上的奇函数f(x)在(-∞,+∞)上递增,若xf(x)-yf(y)>0,那么下列结论中正确的是
( )
A.f(x)
C.f(|x|)
分析 本题综合了函数的单调性和奇偶性,还要用到数形结合的思想方法.构造偶函数g(x)=xf(x),而g(x)在(0,+∞)上递增,由g(x)>g(y)得到|x|>|y|;又f(x)在R上递增,因此f(|x|)>f(|y|).故选D.
例6 设f(x),g(x),h(x)是定义域为R的3个函数,对于命题:①若f(x)+g(x),f(x)+h(x),g(x)+h(x)均为增函数,则f(x),g(x),h(x)中至少有1个是增函数;②若f(x)+g(x),f(x)+h(x),g(x)+h(x)均是以T为周期的函数,则f(x),g(x),h(x)均是以T为周期的函数.下列判断正确的是
( )
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题
分析 本题考查抽象函数单调性和周期性的一般结论.设F(x)=f(x)+g(x),G(x)=f(x)+h(x),H(x)=g(x)+h(x),则

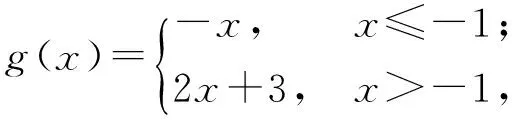
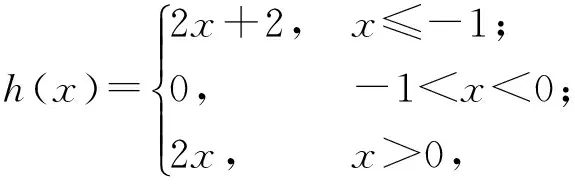
尽管f(x),g(x),h(x)中没有增函数,但它们中任意2个相加均得到增函数,从而命题①的逆否命题是假命题,于是①为假命题.故选D.
3.4 指数函数和对数函数
( )

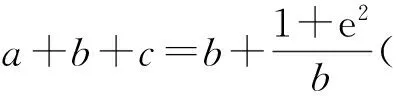
由单调性易知选项B正确.
例8 若x1满足2x+2x=5,x2满足2x+2log2(x-1)=5,则x1+x2=
( )
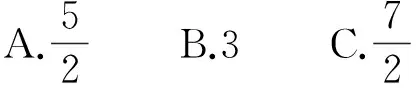
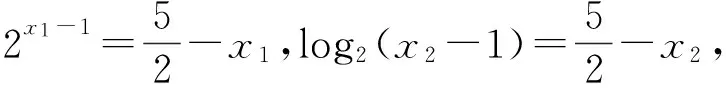
3.5 函数与方程
例9 设f(x)=x2+bx+c(其中b,c∈R),A={x|x=f(x),x∈R},B={x|f(f(x))=x,x∈R},如果A中只含有1个元素,则
( )
A.ABB.BAC.A=BD.A∩B=φ
分析 二次函数的零点式为解决本题带来了便利.显然A⊆B,设A中的元素为t,则
f(x)-x=(x-t)2,
从而
f(x)=(x-t)2+x,
于是方程f(f(x))-x=0可化为
(x-t)2[(x-t+1)2+1]=0,
因此方程只有1个解t,即A=B.故选C.
例10 若二次函数f(x)=ax2+(2b+1)x-a-2(其中a,b∈R,a≠0)在区间[3,4]上至少有1个零点,求a2+b2的最小值.
分析 若先讨论二次方程ax2+(2b+1)x-a-2=0在区间[3,4]上的实根分布得到关于(a,b)的约束条件,再用几何意义求a2+b2的最小值,则过程很繁琐.
本题可变更主元,转化为存在t∈[3,4]使得关于a,b的二元方程(t2-1)a+2tb+t-2=0有解,将点P(a,b)看作直线(t2-1)x+2ty+t-2=0上的动点,则
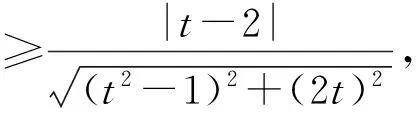
即

因为t-2∈[1,2],所以
从而
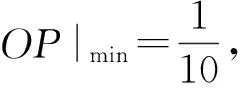
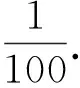
3.6 导数的概念与运算
例11 金属圆盘受热膨胀,面积以π cm2/s的速度增长,求半径等于50 cm时半径的增长速度.
分析 导数的意义是瞬时变化率,除切线的斜率外,还应了解物理情景中的意义.本题中设t时刻,金属圆盘的面积为S(t),半径为r(t),由S(t)=πr2(t),得
S′(t)=2πr(t)·r′(t)=π,
当r(t)=50时,
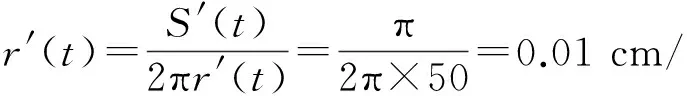
例12 设函数f(x)在R上的导函数为f′(x),且2f(x)+xf′(x)>x2,则下面的不等式在R内恒成立的是
( )
A.f(x)>0 B.f(x)<0
C.f(x)>xD.f(x) 分析 本题不仅考查导数运算法则,还需要根据导数特征构造原函数.因为当x>0时, 2xf(x)+x2f′(x)>x3>0, 即y=x2f(x)在(0,+∞)上递增;同理可得,y=x2f(x)在(-∞,0)上递减,从而f(x)≥f(0).而在2f(x)+xf′(x)>x2中,令x=0可得f(0)>0.故选A. 3.7 函数综合应用 例13 某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(其中e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是______小时. 分析 本题是函数应用题,利用条件可求出参数k,b,但在运算时利用整体代换可不必求出2个参数,使问题大大简化.由题意知 从而 当x=33时, 例14 设函数f(x)=ax+bx-cx,其中c>a>0,c>b>0.若a,b,c是△ABC的3条边长,①对任意x∈(-∞,1)都有f(x)>0;②存在x∈R,使得ax,bx,cx不能构成一个三角形的3条边长;③若△ABC为钝角三角形,则存在x∈(1,2),使得f(x)=0,则上述结论正确的是______(写出所有正确结论的序号). 分析 本题是用函数方法研究不等式问题,而且要将问题转化后重新构建函数来研究.因为 故结论①正确. 因为当x取足够大正数时,g(x)<1,此时 ax+bx 所以结论②正确. 又因为当△ABC为钝角三角形时g(1)>1,g(2)<1,所以存在x∈(1,2),使得g(x)=1,即f(x)=0,故结论③正确. 例15 已知函数f(x)=lnx+ax2+bx(其中a≤0). 1)若2a+b+1=0,讨论函数的单调性; 分析 第1)小题将b=-2a-1代入得 而a≤0,于是当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,因此f(x)在(0,1)上递增,在(1,+∞)上递减. 尝试用数学归纳法证明第2)小题,由假设当n=k时结论成立推证当n=k+1时结论也成立的过程知,要证不等式 只要证 从而只要证当x>1时,lnx 让k取遍1,2,3,…,n,相加即得 进一步探究可得如下结论: 1)当x>1时, lnx 让k取遍0,1,2,3,…,n-1,相加即得 ln(n+1)(其中n∈N*). 让k取遍0,1,2,…,n-1,相加即得 (其中n∈N*),此乃2010年湖北省数学高考理科试题第21题第3)小题的结论. ( ) A.0 B.mC.2mD.4m 2.已知集合U={(x,y)|x∈R,y∈R},M={(x,y)||x|+|y| ( ) A.①②③④ B.①②④ C.①② D.④ 3.设函数ht(x)=3tx-2t2,若有且仅有1个正实数x0,使得h6(x0)≥ht(x0)对任意的正数t都成立,则x0= ( ) A.5 B.6 C.7 D.8 5.R上的偶函数f(x),当x≥0时,f(x)=2x.若对任意x∈[a,a+2],不等式f(x+a)≥f2(x)恒成立,则a∈______. 6.设a,b∈R,若当x≥0时,恒有0≤x4-x3+ax+b≤(x2-1)2,则ab=______. 1)若a=-2,求b的取值范围使函数h(x)=f(x)-g(x)在其定义域上单调递增. 2)设函数y=f(x)的图像C1与函数y=g(x)的图像C2交于点P,Q,过PQ的中点R作x轴的垂线分别交C1,C2于点M,N.问:是否存在这样的点R,使C1在M处的切线与C2在N处的切线平行? 10.已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b. 1)证明:当0≤x≤1时,①函数f(x)的最大值为|2a-b|+a;②f(x)+|2a-b|+a≥0. 2)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围. (2012年浙江省数学高考理科试题第21题) 参 考 答 案 (1) 而 式(2)-式(3),得 由式(1)和式(4)得 即g(t)=(t+1)lnt-2(t-1)在(0,1)上有零点.但当0 g(t) 即g(t)在(0,1)上没有零点. 因此,假设错误,即不存在这样的点R,使C1在点M处的切线与C2在点N处的切线平行. 10.1)略.2)(-1,3]. 2016-12-06; 2016-12-30作者简介:李金兴(1973-),男,浙江杭州人,中学高级教师.研究方向:数学教育. O122.1 A 1003-6407(2017)02-33-05

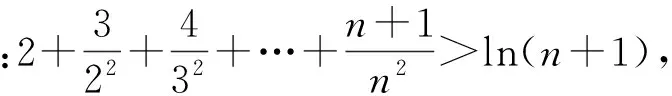


4 精题集萃