椭圆一般弦长公式的妙推及应用

●钟德光 (广州大学数学与信息科学学院 广东广州 510006)

●关丽娜 (深圳大学数学与统计学院 广东深圳 518060)

椭圆一般弦长公式的妙推及应用

●钟德光 (广州大学数学与信息科学学院 广东广州 510006)

●关丽娜 (深圳大学数学与统计学院 广东深圳 518060)

文章给出椭圆一般弦长公式的一个妙推，并借此一般公式，举例说明了它在优化解题步骤和求解圆锥曲线压轴题中的妙用.

椭圆弦长公式；仿射变换；优化解题步骤

1 定理及推论

高中课堂上介绍的椭圆弦长公式虽然形式简单，但缺点是计算量太大，学生也往往因此导致计算失误或者半途而废.因此找到椭圆一般弦长公式显得很有必要.然而这个一般公式是否存在呢？答案是肯定的.文献[1]中给出了答案，只是其中略有缺陷：其一是直线方程不够一般；其二是在推导过程中，应用韦达定理将此公式“硬算”出来,这与数学追求简单的思想有点不对口.因此笔者给出一个原创证明，证明过程采用了仿射变换的性质，优点是可绕开复杂的计算.

为了证明方便，笔者先给出仿射变换的性质.关于仿射变换的性质，读者可在文献[2-3]中找到相关内容.

引理1 2条平行线段经过仿射变换后，依旧是2条平行线段，而且保持线段比例不变.

有了这个引理，就可以着手证明下面的定理：

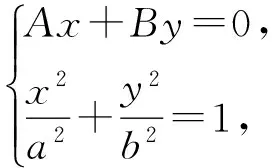
从而

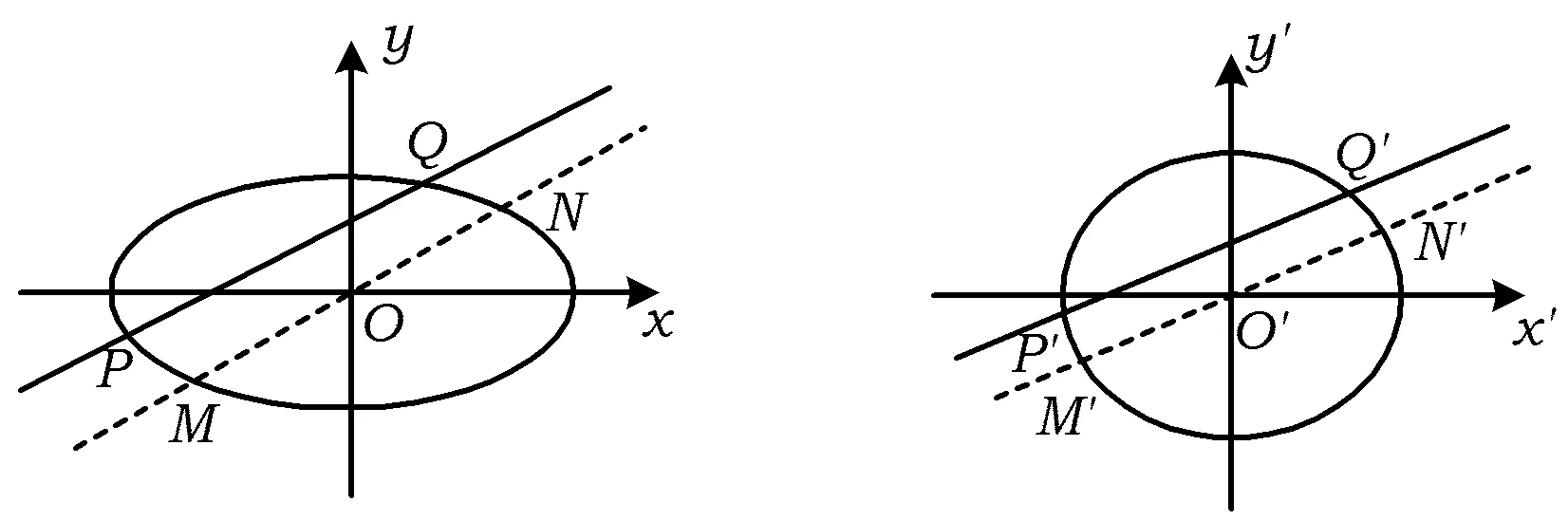
图1 图2

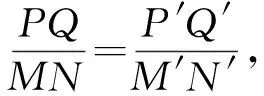
由此定理，我们很容易得到以下几个推论.值得一提的是这些推论都是已知的结果，只是为了行文方便，将它们罗列出来，并且给出粗略的证明.

证明 由定理1可得

设点O到直线l的距离为d，由点到直线的距离公式可得

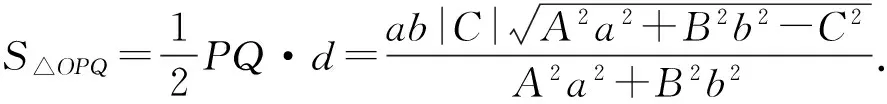
证明 由推论1可知

由基本不等式可得

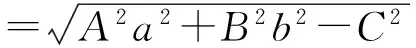
分析 根据条件把直线AB的方程代入一般弦长公式并且稍加整理即可得出结论，此处略去具体证明过程.

A2a2+B2b2-C2≥0.

证明 根据条件，只需要令

即可，容易得到

A2a2+B2b2-C2≥0.

接下来我们通过例子谈谈椭圆一般弦长公式的应用.

2 应用

2.1 优化解题步骤，巧缩计算时间

图3

1)求实数m的取值范围；

2)求△AOB面积的最大值.

(2015年浙江省数学高考理科试题第19题)

2)如图3所示，设点A,B的坐标分别为(x1,y1),(x2,y2)，根据条件可设直线AB的方程为

x+my+k=0.

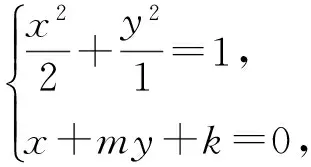
(m2+2)x2+4kx+2(k2-m2)=0.

由韦达定理可得

(2)

(3)

到此为止，我们很有必要停下来谈一谈式(1)、式(2)和式(3).首先，式(1)是由韦达定理得到的，这一步学生一般都能写得出来；其次，式(2)纯粹是课堂上常用的公式，只要学生记得公式就可以直接套用；至于式(3)，学生一般都是将式(1)代入式(2)，再进行化简而得到.但是这种方法不但计算复杂，而且往往会花很多时间，最后还可能得不到|AB|的正确表达式.为了避免这些问题，笔者建议：学生不妨在式(1)、式(2)的基础上，利用定理1得到式(3)，而不再将式(1)代入式(2)化简从而得到式(3).这样不但可以省下许多时间，而且还可以保证计算的正确性，何乐而不为？这里记住定理1的公式是关键.

由基本不等式可得

2.2 巧用极端，妙证切线

证明 设椭圆上任意一点(x0,y0)的切线方程为Ax+By+C=0，则Ax0+By0+C=0.因为直线Ax+By+C=0为切线，故其与椭圆相交所成的弦长为0，所以

A2a2+B2b2=C2.

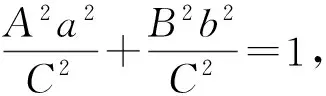
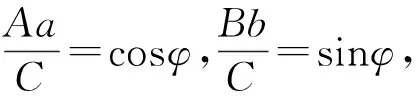
即

cos(φ-θ)=-1,

从而φ=θ+π+2kπ，其中k∈Z，于是

即

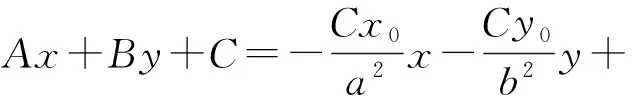
又因为Ax+By+C=0，所以

评注 注意此题2次用到参数方程.

2.3 应用各推论，简解压轴题

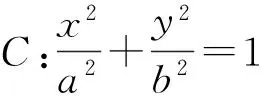
1)求椭圆C的方程.

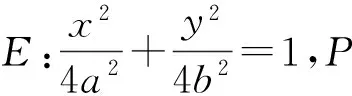
②求△ABQ的最大值.

(2015年山东省数学高考理科试题)

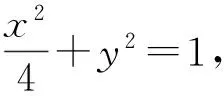
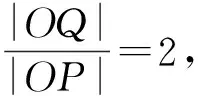
另外，由推论1可得

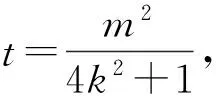
因此

[1] 廖炳江.求椭圆弦长的一个公式[J].安顺师专学报，1999(4)：40-43.

[2] 梅向明，刘增贤，林向岩.高等几何[M].2版.北京：高等教育出版社，2000.

[3] 邓振江.从圆到椭圆的不变性质及其应用[J].中学数学研究，2014(6)：19-23.

2016-10-27；

2016-11-30作者简介：钟德光(1989-),男,广东惠州人,博士研究生.研究方向：教育数学.

O123.1

A

1003-6407(2017)02-17-03