主元反距离加权迭代在病态平差模型中的应用

徐晶鑫，黄其欢

（1. 河海大学 地球科学与工程学院，江苏 南京210098）

主元反距离加权迭代在病态平差模型中的应用

徐晶鑫1，黄其欢1

（1. 河海大学 地球科学与工程学院，江苏 南京210098）

主元加权法在一定程度上克服了最小二乘估计稀疏方差较大的问题，但并没有较好的方法能准确选取权重参数，一定程度上制约了该方法的可用性。引入测量数据中反距离作为增加权重，降低了原主元权重参数的影响，使该方法在解决病态平差线性方程中具有更好的稳定性。

反距离加权；测量平差；主元加权迭代法；病态线性方程

在大数据时代背景下，解算大量线性模型时会遇到一些病态的线性方程组，而通过最小二乘估计等方法对方程进行求解时，估计值会出现严重的偏差，极大地影响了相关科技工作的进展[1]。在测量平差工作中，解决数据之间的病态性，加强数据整体的稳定性是当前不可忽视的一个重要问题。

测量平差中，通过已有观测数据求解拟合模型的系数矩阵时，由于观测数据中存在误差，一旦矩阵行或列向量间有较强的相关性，这些观测矩阵则会呈现病态，即XTX的奇异程度高，使得最小二乘估计的系数方差较大，其模型的普适性较低。现有的解决方法主要包括岭估计、奇异值分解法、遗传算法和误差方程正交化等。岭估计，又称岭回归，是Hoerle于1962 年提出，并由他和Kennard于1970年做了系统的发展[2]。岭估计是一种有偏估计，利用有偏换取平差模型的稳定性。奇异值分解法、遗传算法和误差方程正交化原理复杂，在实际工作中应用不便。文献[3]将主元加权迭代法引入了测量数据的平差处理，采用主元加权的预处理手段，降低系数矩阵的条件数，改善矩阵的病态性；再经过一组迭代公式求解，提高了测量数据的准确性。但是，该方法在选取主元权重参数α时存在确定困难的关键问题，一旦权重参数选取不当，平差数据的精度会大大降低。

本文引入测量数据中的反距离作为增加权重，降低了权重参数α对该方法的决定性作用，根据测量的实际情况选取相应的反距离权重参数P，增强了模型的稳定性。本文分别就良态和病态两种情况选择实例计算，并与高斯约化法、谱修正法进行了对比分析。

1 主元反距离加权迭代法

1.1 反距离权重

设估值点为Q，通过周围测得的观测值来估值计算Q点的近似值，每站观测的距离为d。因为距离不同的观测点对估值的贡献不同，则赋予各参与平差点位数据不同的权重p，将反距离作为估值计算的权重，其一般形式为[4]：

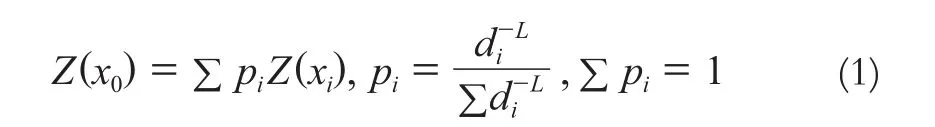
式中，pi为权值；di为i点和待估点的水平距离；L为估值前确定的可变参数。

设估值点为i，则可得到关于距离的权阵为：

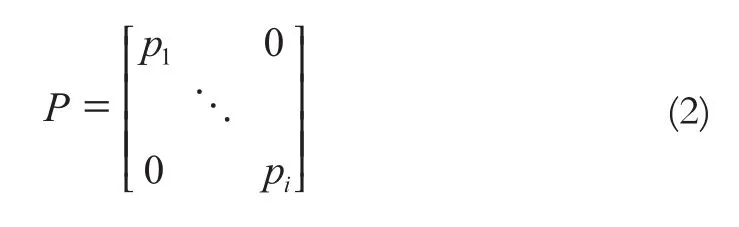
1.2 计算步骤

测量数据处理中存在诸多病态线性方程组，一般形式为：

线性方程组A的内部元素之间存在一定的共线性，即ATA的奇异程度较高，在利用最小二乘估计时其系数方差较大。同时可用矩阵的条件数cond(A)来衡量线性方程的病态性，当矩阵严重病态时，cond(A)＞＞1[5]。

将反距离的权重叠加到主元来改善ATA的奇异程度，即

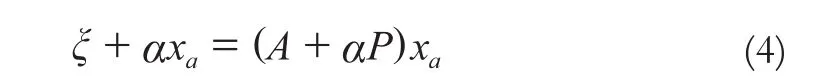
式（4）两边都含有xa可以构造迭代公式：

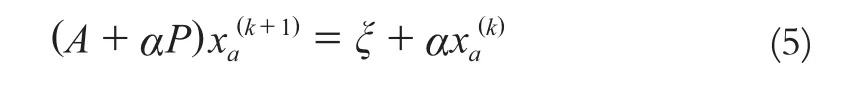
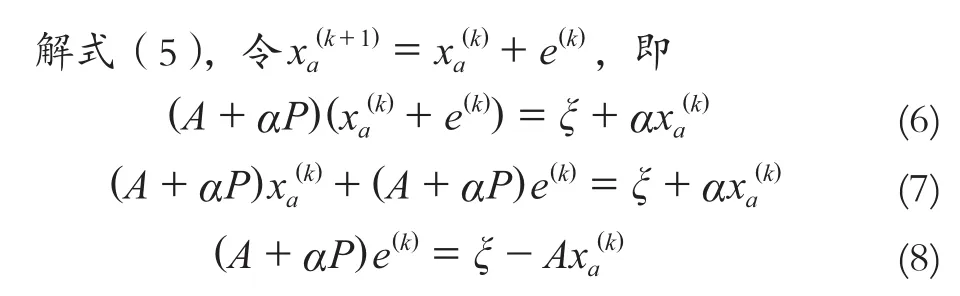
2 算例分析

针对平差方程良态和病态两种情况，通过实例分别分析利用主元反距离加权迭代法、主元加权迭代法、高斯约化法和谱修正法的平差估值效果。

2.1 平差方程的良态问题

本算例取自文献[3]，其法方程为：

此方程为良态方程，利用主元反距离加权迭代法、高斯约化法和谱修正法对方程进行计算，结果见表1。

表1 良态方程计算结果

表1中计算结果完全相同，由此可见，当线性方程良态时，主元反距离加权迭代法可以得到与谱修正法、高斯约化法和主元加权迭代法一致的结果；且与主元加权迭代法相比，主元反距离加权迭代法大大弱化了权重参数α的影响。

2.2 平差方程的病态问题

本算例取自文献[6]，其法方程为：

此方程为病态方程，ATA奇异程度极高。利用高斯约化法、谱修正法和主元反距离加权迭代法分别进行了10次迭代计算，结果见表2。

表2 病态方程计算结果

由表2可知，主元反距离加权迭代法很好地改善了病态平差方程中最小二乘估计，且效果要优于谱修正法和高斯约化法。此外，在病态线性方程组的解算过程中，不在完全受权重参数α的制约，在本算例中，α的选取在1～4之间都能达到较高的方程解算精度。

3 结 语

主元反距离加权迭代法不仅在良态平差线性方程组中与谱修正法、高斯约化法有较为一致的精确解，而且在病态平差线性方程中，能够较好地改善最小二乘估值的解算精度。主元反距离加权迭代法引入反距离作为解算方程的权值，改善了主元加权迭代法原有的解算问题：权重参数的选取。该方法更加具有选择性，减少了对权重参数的依赖性，增加了迭代方程的稳定性，且达到了较高的解算精度。在平差线性方程解算的一般问题中，无论方程有无病态都能通过该方法解算得到较高精度，结合测量工作实际，迭代解算方程简单实用，具有较好的适用性。

[1] 林胜良．病态线性方程组解法研究[D]．杭州:浙江大学,2005

[2] 张勤,张菊清,岳东杰,等．近代测量数据处理与应用[M]．北京:测绘出版社,2011

[3] 王永弟,赵好好．病态线性模型参数估计的主元加权迭代法[J]．测绘通报,2014(2):23-25

[4] 马晨旭,许才军,张琼,等． 引入变差函数的反距离加权法及应用研究[J] ．大地测量与地球动力学,2010,30(1):83-87

[5] 唐丽,李鹏飞． 主元加权迭代法求解病态线性方程组[J]．科学技术与工程,2012,12(2):381-383

[6] 王新洲, 黄海兰, 刘丁酉, 等． 谱修正迭代法及其在测量数据处理中的应用[J]．黑龙江工程学院学报,2001,15(2):3-6

[7] 张杰． 用地球位模型和BP神经网络转换GPS高程[J]．测绘技术学报,2009,26(6):407-409,413

[8] 郭时光． 关于病态线性方程的最小二乘解[J]．科协论坛(下半月),2010(12):76-77

P207

B

1672-4623（2017）01-0072-02

10.3969/j.issn.1672-4623.2017.01.022

徐晶鑫，硕士研究生，主要从事测量数据处理、三维激光扫描等方面的研究。

2015-09-06。

项目来源：国家自然科学基金青年基金资助项目（41304025）。