变形预测模型在地铁保护区监测中的应用

黄 浩，高俊强，苏小文，李 静

（1.南京工业大学 测绘学院，江苏 南京 211816；2.中设设计集团股份有限公司，江苏 南京210014）

变形预测模型在地铁保护区监测中的应用

黄 浩1,2，高俊强1，苏小文1,2，李 静1

（1.南京工业大学 测绘学院，江苏 南京 211816；2.中设设计集团股份有限公司，江苏 南京210014）

结合某地铁保护区隧道监测工程，对沉降数据进行了分析及建模预测，以掌握其变形规律并预测变形趋势。由于单一预测模型存在弊端，较难达到预测要求，所以将灰色预测模型与时间序列模型进行组合，并将新陈代谢的思想引入组合模型进行建模预测。结果表明，新陈代谢灰色-时序组合模型预测结果可靠，具有较高应用价值。

地铁保护区监测；预测模型；灰色-时序组合模型；新陈代谢

随着经济飞速发展，我国城市轨道交通建设取得了一定成绩。地铁的建设缓解了城市交通的压力，也带动了地铁沿线的发展，而地铁周边其他工程项目的施工必然会对地铁隧道产生影响。为保证地铁隧道的安全，在邻近工程施工过程中，对地铁隧道进行精密监测，并对隧道变形趋势进行科学准确地分析及预测就显得尤为重要[1]。变形预测的方法有回归分析、时间序列、灰色预测[2]、人工神经网络、小波变换等。由于变形机理的复杂性，单一预测模型较难满足预测要求。为最大限度地挖掘单一模型蕴含的信息，提高预测精度，本文建立了灰色-时序组合预测模型，并将新陈代谢思想引入组合模型中，最后通过工程实例进行了验证。

1 新陈代谢灰色-时序组合模型

1.1 沉降数据的GM(1,1)模型

灰色预测模型是由我国著名学者邓聚龙教授提出的，用以对既含有已知信息又含有未知或非确定信息的系统进行预测[3]。该模型对建模数据的要求低，可直接处理非平稳数据；且所需数据量较小，信息利用率高[4]。最常用的灰色预测模型为GM(1,1)模型。

设原始观测序列为：

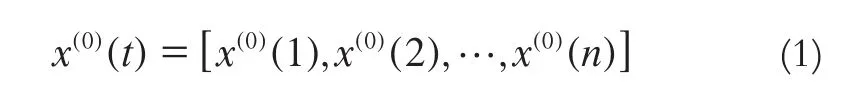
对原始观测序列进行一次累加，得到递增序列为：

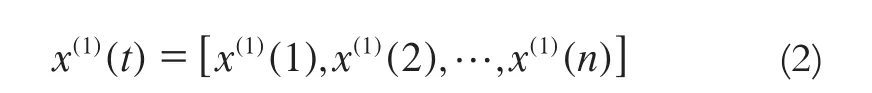
累加序列的一阶线性微分方程为：

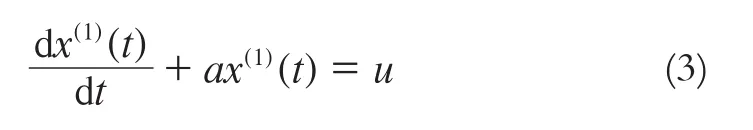
式中，a为发展系数；u为灰色作用量；a、u均为待定常数。可由最小二乘原理求得：

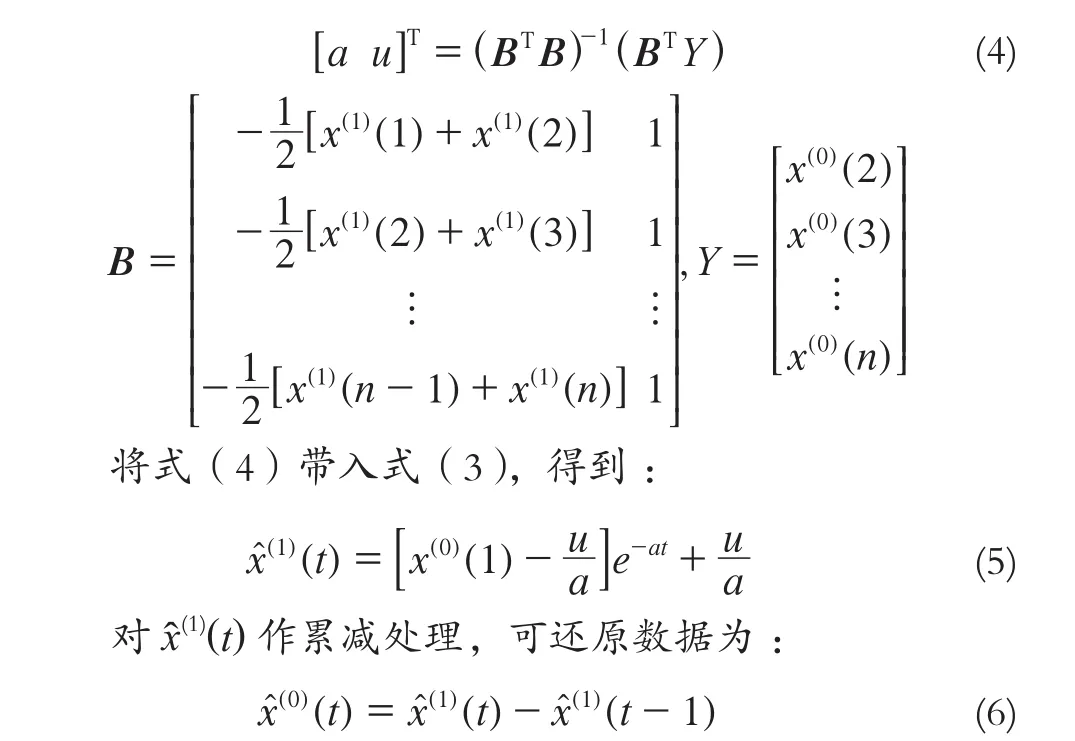
1.2 分离趋势项

沉降量序列是由沉降量趋势项和沉降量随机项构成的[5]，即

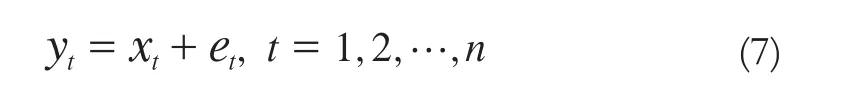
式中，yt为沉降量序列；xt为趋势项；et为随机项。

GM(1,1)模型可直接处理非平稳的时间序列，将沉降数据进行GM(1,1)建模处理，得到趋势项；但GM(1,1)模型并未对et进行处理，因此单一的GM(1,1)模型预测精度并不高。

1.3 对et建立自回归模型

et为稳定的时间序列，对其建立阶数为p的自回归模型，阶数p可由AIC准则确定[6]。

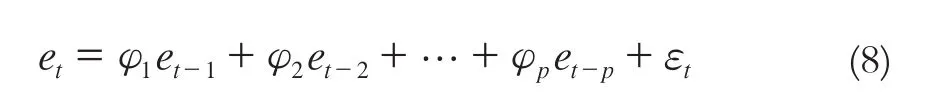
可由最小二乘原理求得参数的估值，从而得到et。

综上，可将式（7）写成为：

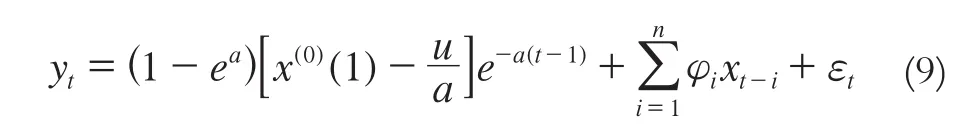
式（9）即为灰色-时序组合模型的预测式。其实质为先运用GM(1,1)模型对非平稳序列进行预处理，再对平稳的et建立自回归模型；亦可理解为一个具有指数趋势项的时间序列模型。

1.4 将新陈代谢思想引入组合模型

由式（9）可建立灰色-时序组合模型对监测点的沉降量进行预测。但随着监测数据的逐渐增多，预测数据和实测数据相距渐远，且原预测模型不能随时间推移而改进[7]。若直接套用原模型进行预测，其预测精度得不到保证。为解决此问题，本文将生物学中新陈代谢的思想引入灰色-时序组合模型，即不断吸收新信息，淘汰旧信息，并保持相同维数。新陈代谢灰色-时序组合模型建模过程为：

2 工程实例

2.1 工程概况

某基坑项目位于某市地铁一号线某区间西北侧，开挖深度约为6 m。基坑邻近地铁侧支护结构外边线，离地铁隧道外边线最近距离约为10．9 m。基坑边线对应地铁左线里程为ZK20+218．85～ZK20+301．35，长度为82．5 m；地铁右线里程为YK20+226．50～YK20+312．50，长度为86．0 m。监测范围为基坑边线对应地铁线路里程及前后外放40 m范围，左线为162．5 m，右线为166．0 m。

2.2 新陈代谢灰色-时序组合模型建模及预测结果

由于监测点较多，选取较具有代表性的Y10点，对其前6期数据进行分析。通过监测点的累积沉降值进行建模，分别使用GM(1,1)模型、灰色-时序组合模型、新陈代谢灰色-时序组合模型对累积沉降量进行预测。运用 Matlab 进行计算[8]，可得Y10点3种模型的预测值和残差值，如表1所示。

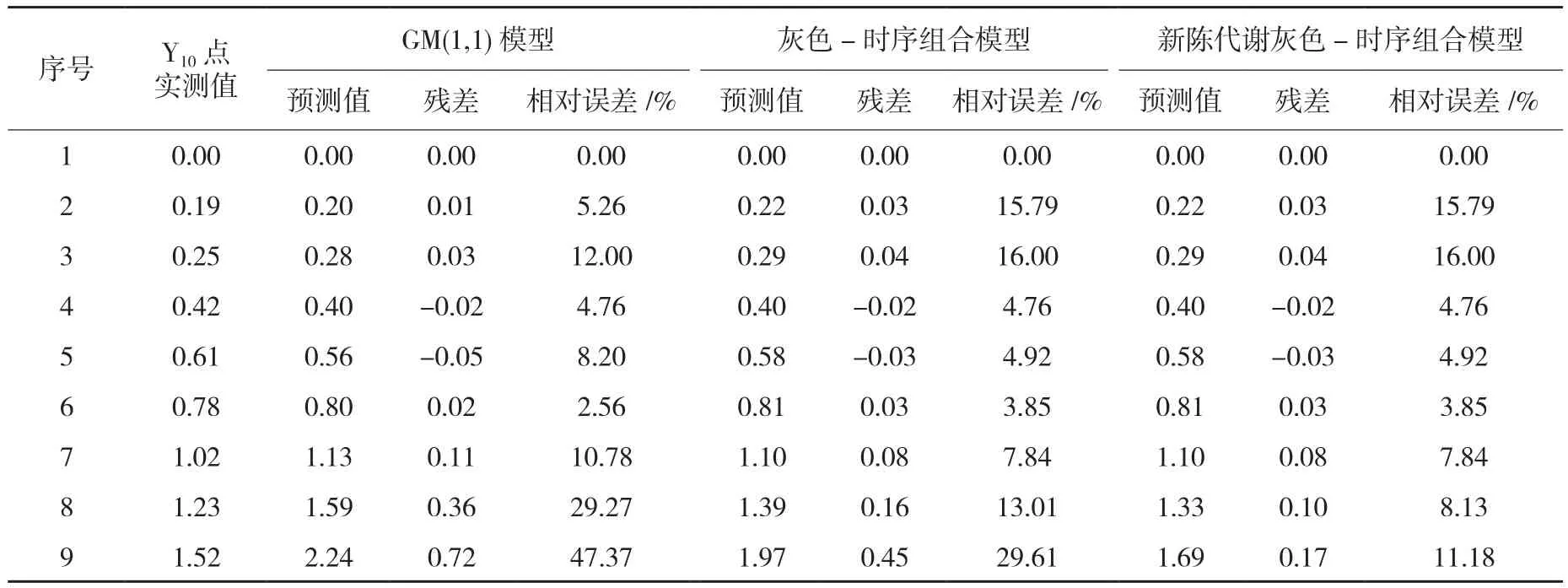
表1 Y10点3种模型的预测值及残差值/mm

从表1可以看出，GM(1,1)模型预测残差最大值达到0．72 mm，且从第7～9期残差值增幅较大。组合模型相对于GM(1,1)模型预测精度均有提高，结果更接近实测值。灰色-时序组合模型和新陈代谢灰色-时序组合模型第7～8期的预测精度较高，残差值均小于0．20 mm；特别是新陈代谢灰色-时序组合模型第7～8期的残差值最大为0．10 mm，表明两种组合模型的短期预测均可靠。当预测第9期数据值时，GM(1,1)模型的残差值为0．72 mm，相对误差为47．37%，灰色-时序组合模型的残差值为0．45 mm，相对误差为29．31%，误差精度都很难达到要求；而新陈代谢灰色-时序组合模型的残差值仅为0．17 mm，相对误差仅为11．18%，相对于GM(1,1)模型和灰色-时序组合模型预测结果更为可靠。

由图1可看出，进行第7期数据预测时，3种模型的预测结果均接近实际沉降值，效果较好；进行第 8期数据预测时，GM(1,1)模型预测结果偏离实际沉降值较多，结果不够理想，灰色-时序组合模型与新陈代谢灰色-时序组合模型的预测结果仍接近实际沉降值；进行第9期数据预测时，GM(1,1)模型与灰色-时序组合模型的预测结果均已偏离实际沉降值较多。新陈代谢灰色-时序组合模型由于不断引入最新数据、淘汰旧数据，其预测结果更接近实际沉降值，更为可靠。

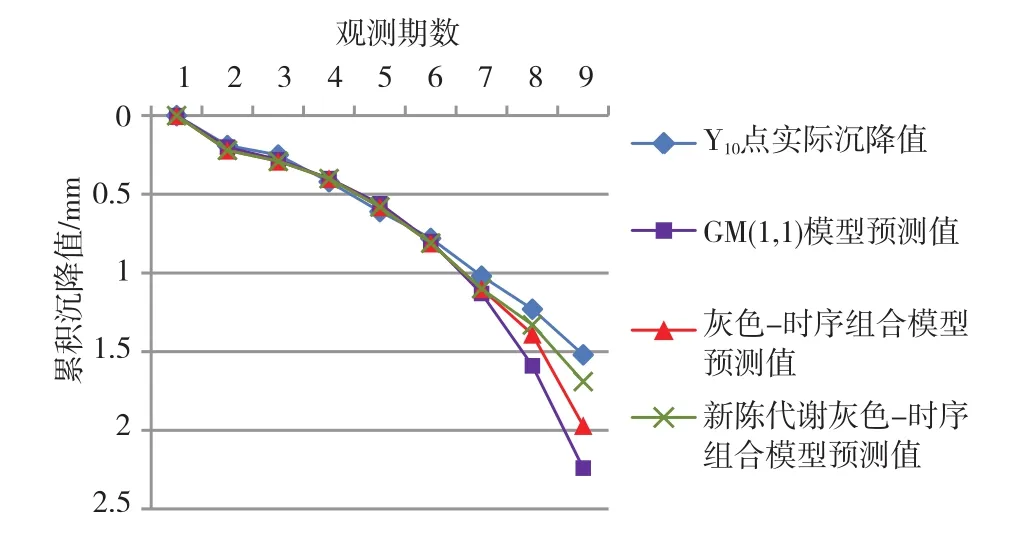
图1 Y10点累积沉降值及3种模型预测值

3 结 语

当数据量较小时，GM(1,1)模型可对后期数据进行预测。但单一的GM(1,1)模型预测精度不高。灰色-时序组合模型充分利用了GM(1,1)模型与自回归模型，更好地反映了实际沉降规律，在中短期预测时精度较高；但由于未及时进行数据更新，在进行长期预测时，效果并不理想。新陈代谢灰色-时序组合模型在灰色-时序组合模型的基础上，及时引入了最新的监测数据，淘汰旧的监测数据。实例数据表明，新陈代谢灰色-时序组合模型在中短期预测、长期预测中均取得了较可靠的预测结果，在类似的地铁保护区变形预测分析中具有较高的应用价值。

[1] 于来法．论地下铁道的变形监测[J]．测绘通报,2000(5):13-15

[2] 袁明月,周吕,文鸿雁,等．灰色系统与时间序列在高铁沉降变形中的应用[J]．地理空间信息,2013,11(4):131-133

[3] 邓聚龙．灰色预测决策[M]．武汉:华中理工大学出版社,1988

[4] 陈伟清,田海涛,陈佳佳．工程建筑变形分析的灰色模型探讨[J]．广西大学学报(自然科学版),2011,36(1):64-70

[5] 王磊,陈伟清,刘国献,等．灰色自回归模型的建筑物沉降预测探讨[J]．测绘科学,2013,38(2):125-127

[6] 何超,黄声享,陈启文,等．基于数据残差的AR模型在高铁路基沉降预测中的应用[J]．测绘工程,2011,20(5):53-56

[7] 孙泽信,庞逸群,黄腾．改进的灰色模型在建筑物沉降预测中的应用[J]．测绘工程,2010,19(3):59-62

[8] 陈健．Matlab在变形监测数据处理中的应用[J]．城市勘测, 2009(2):130-133

P258

B

1672-4623（2017）01-0104-03

10.3969/j.issn.1672-4623.2017.01.032

黄浩，硕士研究生，主要从事工程测量等科研和应用方面工作。

2015-01-15。