基于实际数据的宏观基本图磁滞现象及分析

付 强，田光华，焦小龙

（1.同济大学测绘与地理信息学院，上海市 2 00092；2.同济城市规划设计研究院，上海市200092）

基于实际数据的宏观基本图磁滞现象及分析

付 强1，田光华2，焦小龙2

（1.同济大学测绘与地理信息学院，上海市 2 00092；2.同济城市规划设计研究院，上海市200092）

宏观基本图理论为路网管理研究提供了新的简单的数学工具，可大大减少路网分析的复杂性。宏观基本图磁滞现象是这一理论的基本问题之一。利用上海市快速路网的实际数据，首先验证了宏观基本图的存在，并选取典型路段的检测器，通过小范围的集计，可以归纳得出宏观基本图磁滞的原因。研究发现，检测器之间拥堵的不同步是造成磁滞的主要原因之一，磁滞圈的大小与拥堵的持续时间有关。

交通工程；宏观基本图；磁滞

0 引言

从20世纪60年代起，交通学者提出网络通行能力的模型，开启了路网宏观交通流模型研究的历程。之后，流量-速度的线性模型、α关系模型和二流理论陆续被建立起来。这些早期模型为网络交通效果的评价提供了基本理论和基本方法，但这些模型存在数据精度差、参数难以观测等缺陷，且不适用于拥堵路网。以往的交通政策和措施的评估严重依赖于预测模型（prediction-based models），但这些模型对数据要求高，而且对于饱和网络预测精度差。基于以上原因，Daganzo[1]转而提出基于监测的模型（observation-based models），通过实时检测和控制路网内的车辆总数，使得路网的通行能力最大，且该模型独立于交通需求（OD表），与传统基于预测的路网研究相比，不需要如此多的参数和驾驶员路径选择等行为的分析，从而使得建模重点从微观预测转至宏观状态监测与控制。而且，宏观基本图是在一定控制管理手段下，路网的本质属性对OD不敏感，且与需求变化无关。利用宏观基本图对路网进行研究，可以大大简化路网整体分析的复杂性，为宏观层面的路网管理研究提供了新的简单的数学工具。正因为这一原因，对宏观基本图理论的研究迅速成为当前的研究热点。

宏观基本图理论提出后，Daganz o[2]通 过CORSIM仿真发现，当路网各路段均匀拥堵时，路网中所有车辆行驶的总距离P和路网内车辆的数量存在函数关系，并且路网驶出流量与车辆行驶的总距离P存在简单的线性关系。Geroliminis和Daganzo[3]分析横滨市的检测器和出租车数据，发现区域路网内流量、密度和速度之间存在着简单的关系，即宏观基本图，可见随着占有率的增加，路网的平均流量先增加后减小，路网的MFD呈现一个单峰的曲线。此外，文中也验证了路网驶出流量和路网平均流量之间的正比例关系。随后，Gonzales等[4]通过仿真研究验证了内毕罗路网中MFD的存在性。Gao Feng[5]运用FCD数据验证斯德哥尔摩路网中也存在MFD。MFD建立了路网运行状态和路网交通量之间的联系，是网络交通流的重要特性，对于路网范围内的交通管理和控制具有重要意义。

MFD被提出之后，相关学者发现宏观基本图存在磁滞现象，并引起广泛关注。磁滞现象被认为是由路网密度分布的均匀性引起的，由此引起了对路网密度不均匀性影响的研究。Buisson和Ladier[6]分析法国图卢兹的检测器数据，发现路网MFD的磁滞现象（见图1），可见随着时间的推进，路网平均流量与平均密度的关系折线形成一条闭合的环线，而不是线性曲线。该研究认为，磁滞现象是由密度不均匀性引起的。Mazloumain等[7]通过仿真分析发现，密度的不均匀分布增加路段流量溢出的概率，成为影响路网交通流状态的重要因素。Daganzo等[8]通过仿真研究发现如果密度足够高，那么路网处于稳定的平衡状态时密度呈现不均匀分布，与密度均匀分布的路网相比，处于这种平衡状态的路网流量更低，并呈现多值性。Geroliminis等[9]分析双城大都市区的高速公路数据，发现交通量时空分布的不均匀性是影响MFD离散性和形状的重要因素。Geroliminis[10]运用双城大都市区的高速公路数据，发现高速公路的MFD离散且存在磁滞现象，认为磁滞现象的原因是拥堵消散时密度的不均匀分布以及同时出现的capacity drop现象。Gayah等[11]运用two-bin model证明，与拥堵形成期间相比，在拥堵消散期间路网的交通量更容易不均匀分布，因此路网的MFD容易出现顺时针的磁滞现象。Daganzo[12]发现需求均匀的高速公路中，交通拥堵消散期间密度分布也不均匀，从而出现磁滞现象。

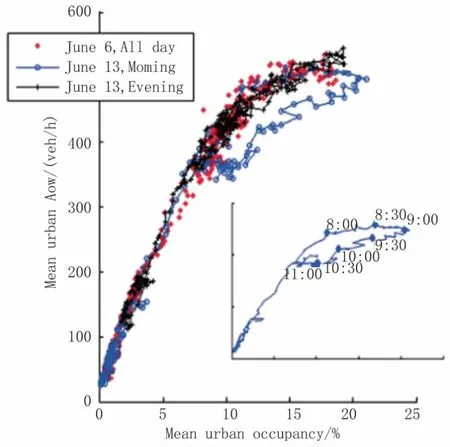
图1 MFD的磁滞现象（图卢兹，2008）

磁滞现象是宏观基本图的一个重要研究方向，研究磁滞现象的产生机理，发现其对路网运行的影响，对于城市路网的管理具有重要意义。但是，当前对磁滞现象的研究，仍集中于两点：一是宏观基本图磁滞是否存在，多数学者是通过本地的线圈数据，证明磁滞的存在；另外一点则是研究磁滞的形状特点，及其与部分交通参数，如密度的关系。对于磁滞现象的产生机理，仍然缺乏足够的研究。基于以上考虑，本文利用上海快速路检测器的实际数据，从不同集计范围进行对比，以图发现宏观基本图磁滞的微观机理。

1 上海市快速路网宏观基本图特征

1.1 数据采集时间及地点

为分析我国城市路网，特别是快速路网的宏观基本图特征，以上海市浦西外环以内（不包含）的快速高架路为研究对象（见图2a），具体包括：内环高架、中环高架、延安高架、逸仙高架、沪闵高架和南北高架，直道限速为80 km/h，弯道限速为60 km/h。由于双向交通严格隔离，快速路两个方向的路段数据分开统计。

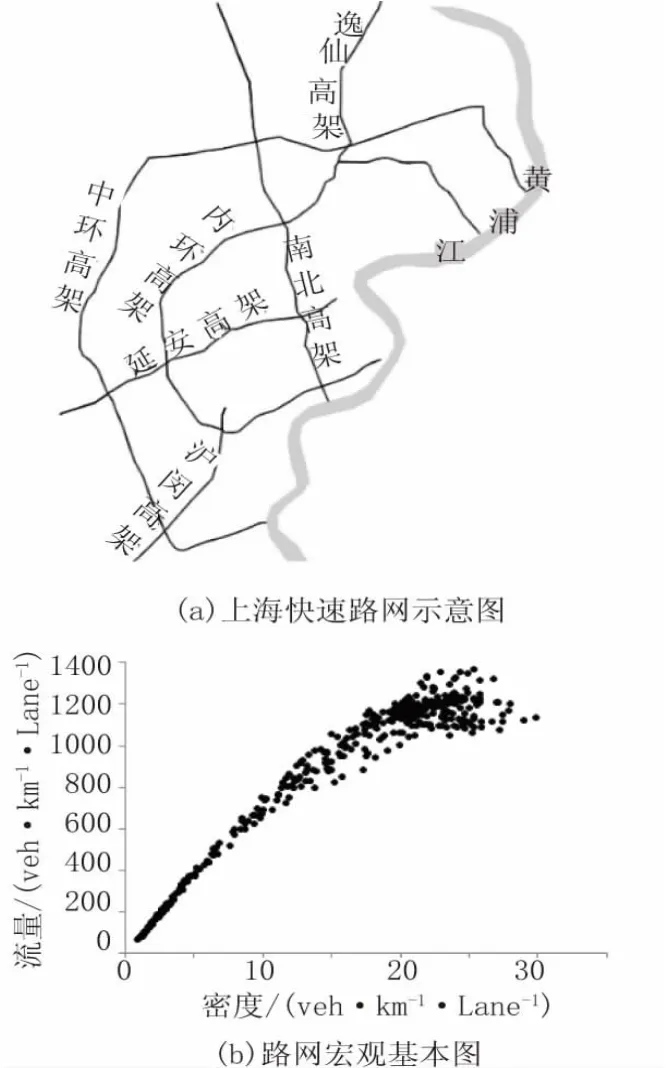
图2 上海快速路网及其宏观基本图

本文所用的数据为单向路段全天24 h的流量和速度，分别采集自2013年5月12日至18日、2014年5月12日至17日（5月14日数据缺失）和2015年5月10日至16日（5月14日数据缺失），共计18天。数据统计周期为1 h，其中凌晨0：00-1：00的速度数据均存在明显异常，在数据处理中予以剔除。尽管数据的统计周期为1 h，但数据在空间范围上是一致的，在时间上是连续的，可以反映路网宏观交通流状态的变化，因此可以用来分析路网的宏观基本图规律。

1.2 数据分析方法

在微观交通流理论中，交通流基本图通常用来描述单条路段的交通流规律。近年来的研究发现，区域路网的平均流量、平均密度和平均速度也存在类似的关系，描述路网交通流参数关系的坐标图为路网宏观基本图。其数据集计方法如下。

根据公式（1）、（2）计算每个统计周期内路网的平均流量和平均密度，平均的权重是路段的车道长度。

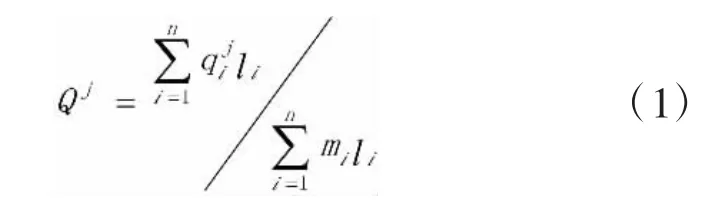
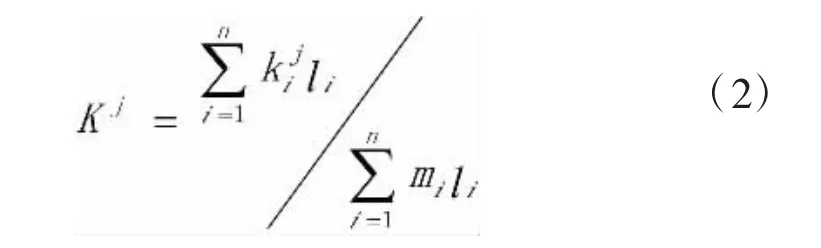
式中：Qj和Kj分别为第j个统计周期内路网的平均流量和平均密度；qji和kji分别为第j个统计周期内路段i的流量（同向所有车道）和密度（同向所有车道）；mj和lj分别为路段i的车道数和长度，n为路段数量。

图2b为使用18天检测器数据绘制的路网宏观基本图，一个数据点代表某个统计周期内路网的宏观交通流状态。可见，路段交通流参数经过集计之后，存在于单条路段基本图中的散点消失，路网的宏观基本图呈现较为清晰的曲线。这表明相比于路段，路网具有更加稳定的流量-密度关系，路网内存在宏观基本图。同时，通过图2b还可以看出，宏观基本图在顶部仍然存在一定的离散，而不是良好的基本图，同国外的情况对比说明，我国的快速路宏观基本图也存在磁滞现象。

2 宏观基本图磁滞分析

宏观基本图磁滞现象是宏观基本图理论的基础问题之一，但至今为止，仍没有合理的解释。以往的学者多是证明宏观基本图磁滞现象的存在，或者从统计学角度寻找其与密度等参数的关系，但是对其产生的机理缺乏足够的研究。事实上，微观交通流基本图中，也存在磁滞现象，目前较为可信的解释是张红军教授提出的加减速不对称理论，即在加速和减速阶段，驾驶员的行为具有不对称性。根据宏观基本图的定义，其流量、密度、速度是微观交通参数的集计平均，因此，在分析宏观基本图磁滞成因时候，可以从两个角度进行分析：一是这种磁滞是否是因为微观磁滞的影响，即每个检测器所得的微观基本图本身存在磁滞，由此带来了宏观基本图磁滞；另外一个可能的原因则是，微观基本图不存在磁滞，在集计过程中产生了宏观基本图磁滞现象。

为分析宏观基本图磁滞产生的原因，从上海快速路中选取了南北高架的一段，如图3所示。选取的检测器为南北高架东线徐家汇上匝道上下游的检测器，编号依次为NBDX03，NBDX04，NBDX05，NBDX06，其中03和04号检测器在合流区的上游，05和06检测器在合流区的下游。检测器之间的距离在500 m左右。通过这几个检测器自身的微观基本图和其按照宏观基本图的定义集计后产生基本图进行对比，探寻宏观基本图的产生原因。

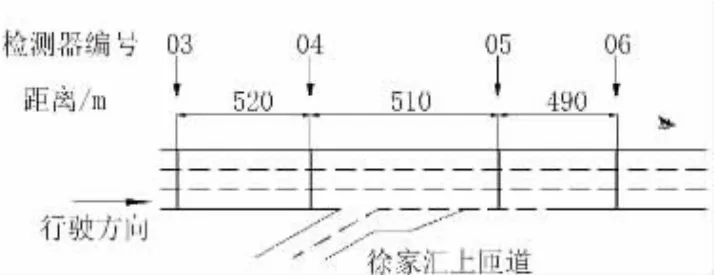
图3 宏观基本图磁滞分析选取路段及检测器

考虑到通常上午和下午的流量变化情况不同，放在一起容易互相干扰，因此选取上午0:00-12：00的数据。不同检测器在这段时间的流密图如图4所示。

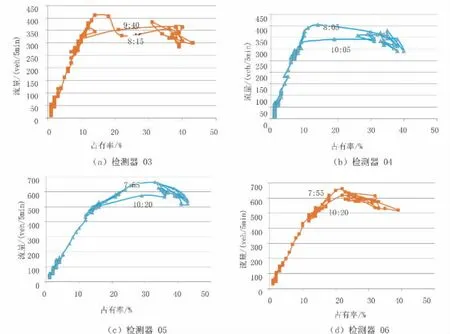
图4 不同检测器的流密图

在图4中，我们可以看到，每个检测器的流密图中，都存在中间状态点，称之为“状态过渡点”。为研究方便，将“状态过渡点”的时间标出，因为这一类点通常是畅通和拥堵的过渡点，其时间可以表征此点进入拥堵和拥堵消散的时间。从图5可以看出，不同检测器进入拥堵状态的时间不同，检测器05和06都在7:55最早进入拥堵状态，而检测器04于8:05进入拥堵状态，检测器03进入拥堵状态最晚，为8:15。拥堵消散的时间则相反，检测器03于9:40拥堵消散，检测器04于10:05拥堵消散，而检测器05和06都于10:20拥堵消散。这也符合我们通常的认知，与图4中的实际流量变化曲线相符合。

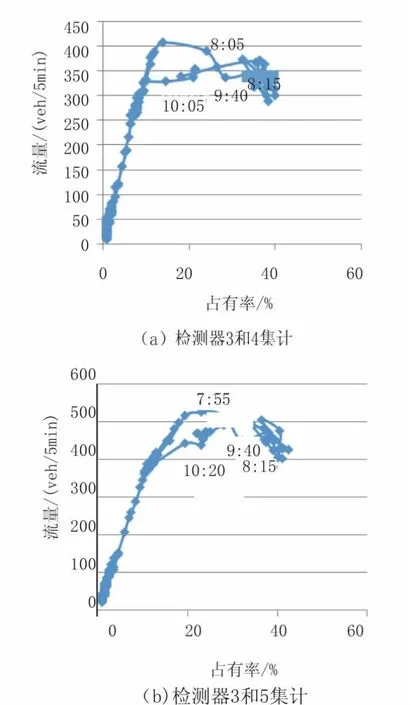
图5 集计后的磁滞示意图

从上面图中可以看出，单个检测器的流密图严格来说不存在磁滞现象，而只是存在过渡状态点，即从畅通到拥堵或者是从拥堵到畅通转变时，中间时段的参数。接下来我们看不同检测器集计后会否产生磁滞，首先看检测器3和检测器4，其集计后的基本图如图5所示。

从图5a可以看出，检测器03和04集计后的基本图会出现磁滞，而且，其磁滞的前半段始于8: 05，止于8:15，正是检测器04和检测器03分别进入拥堵状态的时间。从8:15到9：35，集计点都在拥堵状态，即在曲线的右半段。磁滞的后半段始于9：40，结束于10：15，则正是检测器03和04分别从拥堵状态消散的时刻。图5b也呈现同样的规律。可见，当两个检测器所在的交通流拥堵不同步时，经过集计，即会形成磁滞，虽然只采用了两个检测器，但是根据宏观基本图的定义，多个检测器获得的数据集计时，拥堵不同步也会是造成磁滞的原因之一。

检测器05和06的集计基本图如图6所示。

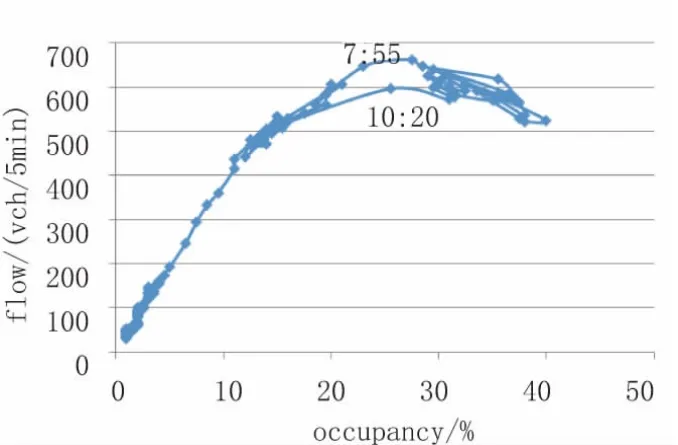
图6 检测器05和06参数集计获得的基本图

检测器05和06由于进入拥堵状态和拥堵消散的时刻相同，因此，没有出现磁滞，其出现的中间状态点只有一个，且是由于检测器05和检测器06的数据中存在过渡点而得到的。因此，当检测器的状态变化一致的时候，不会出现磁滞（如果认为过渡点算微观磁滞的话，则只要有拥堵就会有磁滞，因为最后恢复的时候，连线必然低于原来的，只是没有中间状态点）。

3 结论

宏观基本图理论为路网分析提供了全新的方法和思路，但以往研究仍集中于宏观基本图的存在性验证，宏观基本图磁滞现象也是研究的热点之一，相较于其他学者所采用的统计学方法分析磁滞产生的原因，本文采用实际数据，基于归纳法的原理，较为直观地说明了磁滞形成的原因。通过本文的研究发现，单个检测器本身是否存在磁滞与宏观基本图磁滞没有必然联系，而不同检测器之间拥堵时间的不同步是形成宏观基本图磁滞的原因之一，但不能排除其他原因。因此，当存在拥堵，且拥堵不同步时，宏观基本图磁滞即会发生。良好的宏观基本图（不存在磁滞）很难存在，只有城市交通管理到某一阶段，使得整个路网拥堵非常均匀或者不存在拥堵时，才会获得良好的宏观基本图。

[1]Daganzo C F.Urban gridlock:Macroscopic modeling and mitigation approaches[J].Transportation Research Part B,2007,41(1):49-62.

[2]Geroliminis N,Daganzo C F.Macroscopic modeling of traffic in cities[C]//Transportation Research Board 86th Annual Meeting, 2007.

[3]Geroliminis N,Daganzo C F.Existence of urban-scale macroscopic fundamental diagrams: Some experimental findings [J]. Transportation Research Part B,2008,42(9):759-770.

[4]Gonzales E J，Chavis C，Li Y，Daganzo C F.Multimodal Transport Modeling for Nairobi,Kenya:Insights and Recommendations with an Evidence-Based Model[R].UC Berkeley Center for Future Urban Transport,2009.

[5]Feng G.Macroscopic Fundamental Diagrams for Stockholm Using FCD Data[D].KTH:Royal Institute of Technology,2011.

[6]Buisson C,Ladier C.Exploring the Impact of Homogeneity of Traffic Measurements on the Existence of Macroscopic Fundamental Diagrams [J].Transportation Research Record Journalofthe Transportation Research Board,2009（2124）:127-136.

[7]Mazloumian A,Geroliminis N,Helbing D.The spatial variability of vehicle densities as determinant of urban network capacity[J]. Philosophical Transactions of the Royal Society A Mathematical Physical&Engineering Sciences,2010,368(1928):4627-4647.

[8]Daganzo C F,Gayah V V,Gonzales E J.Macroscopic relations of urban traffic variables:Bifurcations,multivaluedness and instability [J].Transportation Research Part B,2011,45(1):278-288.

[9]Geroliminis N,Sun J.Properties of a well-defined macroscopic fundamental diagram for urban traffic[J].Transportation Research Part B,2011,45(3):605–617.

[10]Geroliminis N,Sun J.Hysteresis phenomena of a Macroscopic Fundamental Diagram in freeway networks [J].Transportation Research Part A,2011,45(9):966-979.

[11]Gayah V V,Daganzo C F.Clockwise hysteresis loops in the Macroscopic Fundamental Diagram: An effect of network instability [J].Transportation Research Part B,2011,45(4): 643-655.

[12]Daganzo C F.On the macroscopic stability of freeway traffic[J]. Transportation Research Part B,2011（45）:782-788.

U491

A

1009-7716（2017）01-0125-04

10.16799/j.cnki.csdqyfh.2017.01.037

2016-12-05

国家自然科学基金（51308409）；中国博士后科学基金（2013M541545）

付强（1979-），男，山东淄博人，博士后，高级工程师，主要研究方向为交通行为和交通信息。