广义线性模型在林火发生预报中的应用

张洁，赵浩彦*，张民侠，李晨阳，陈戈萍

(1.南京森林警察学院，南京210023；2.山西省森林防火预警监测中心，太原030012)

广义线性模型在林火发生预报中的应用

张洁1，赵浩彦1*，张民侠1，李晨阳2，陈戈萍1

(1.南京森林警察学院，南京210023；2.山西省森林防火预警监测中心，太原030012)

首先介绍了国内外广义线性模型在林火发生预报中的应用，其次分别阐述了常用于林火发生预测的正态分布、逻辑斯蒂分布、泊松分布、负二项分布、零膨胀、栅栏等6种广义线性回归模型的表达式、参数估计方法和几种相关的假设检验方法，其中，逻辑斯蒂广义线性模型主要用于预测林火发生的概率，其他5种模型主要用于预测林火发生的频次。根据林火发生频次的数据结构特点和前人的研究结果分析得出，与正态分布相比，泊松分布、负二项分布、零膨胀、栅栏4种广义线性回归模型更适于预测林火发生的次数。当林火发生频次的方差接近于期望，应采用泊松或零膨胀泊松广义线性模型；如林火发生频次的方差显著大于期望，则宜采用负二项或零膨胀负二项广义线性模型。最后，对广义线性模型在我国林火发生预测中的应用提出了三方面建议：第一，增加模型的自变量(如森林可燃物特征、地形、人类活动等因子)；第二，增加模型在景观层次林火发生预报中的应用；第三，拓展模型的建模方法，如建立广义线性混合效应模型和广义相加模型。

广义线性模型；泊松回归模型；负二项分布回归模型；零膨胀模型；栅栏模型

林火发生预报是一种通过综合考虑天气变化、可燃物干湿程度变化和可燃物类型及火源出现的危险等因素来预测预报火灾发生可能性的方法[1]。林火发生预报是在火险预报的基础上进行的，要求预报出某一地区、某一时间段内林火发生的概率或次数。与火险天气预报相比，林火发生预报不仅需考虑气象因素，同时还需要考虑可燃物、地形、人类活动等因素，因此，其得出的结论较为全面、准确。

为了精确预测林火的发生，通常需要建立林火发生概率(或次数)与气象、可燃物、地形、人类活动等因子的相关关系模型。由于林火发生概率和次数不满足“正态、等方差”的特点，因此，传统回归模型不适于预测林火发生的概率和次数。针对林火发生的数据特点，越来越多的国内外学者使用广义线性模型来预测林火的发生。

笔者在介绍正态分布、逻辑斯蒂分布、泊松分布、负二项分布、零膨胀、栅栏等广义线性模型公式和应用情况的基础上，分析比较这些模型的精度，找出最适于预测我国林火发生的模型，并针对广义线性模型在我国林火发生中的应用现状，提出相应的改进措施。这对于提高我国林火发生预测的精度，更好地开展我国林火预警工作具有极为重要的意义。

1 广义线性模型在林火发生预报中的研究进展

早在1919年，Fishar就开始使用广义线性模型，直至1972年，Nelder等[2]首次引入广义线性模型(generalized linear models，简称GLM)的概念，并建立了统一的理论和计算框架。1983年，McCullagh等[3]出版了详细论述广义线性模型的基本理论与方法的专著，首次系统地总结了广义线性模型的性质和特点。

国外很早就将广义线性回归模型应用到森林火灾的预测领域。1954年，Crosby[4]开始运用泊松回归模型和负二项回归模型预测林火的发生次数。Dayananda[5]运用泊松回归模型拟合了林火发生次数与火灾危险指数之间的相关关系。Wotton等[6]使用泊松回归模型预测了雷击火的发生。Mandallaz等[7]运用泊松回归模型拟合了林火发生次数与干旱指数、气象因子之间的相关关系，他们认为泊松模型中把火险指数和其他重要的解释变量加以合并的结果通常要优于经验方法中单独使用火灾隐患指数。Wotton等[8]通过建立泊松模型预测了2020—2040年穿过北美安大略湖的森林防火生态区的林火发生次数。Symington[9]运用负二项模型预测了安大略省帕里桑德地区林火发生的次数。缪柏其等[10]分别建立了预测日本全国每日发生林火次数的逻辑斯蒂和零膨胀泊松回归模型。

而且国外很多学者采用Logistic广义线性模型预测了林火发生的概率。Vilar等[11]建立了预测西班牙马德里地区人为火发生概率的Logistic模型。Gudmundsson等[12]以标准降雨因子(SPI)为自变量，建立了预测南欧每月林火发生概率的Logistic模型并取得了较好的预测效果。Alencar等[13]以到主路的距离、到林缘的距离、景观片段大小因子等因子为自变量建立了用于预测亚马逊东部流域地表火发生的Logistic概论模型并取得了较好的预测效果。Díaz-Avalos等[14]建立了预测美国俄勒冈州蓝岭山区不同区域雷击火发生概率的Logistics多层广义线性混合效应模型，并分析了不同植被类型、高程、坡度和降雨量对雷击火发生概率的影响。Preisler等[15]建立了用于预测美国俄勒冈州1 km×1 km的单元区域内每天森林火灾发生概率的Logistics广义相加模型。

我国应用广义线性回归模型进行森林火灾预测起步较晚，20世纪初才开始进行相关研究。郭福涛等[16-17]采用泊松、负二项、零膨胀泊松、零膨胀负二项4个模型拟合了大兴安岭地区每月林火发生频次和主要气象因子的相关关系。秦凯伦等[18]采用零膨胀泊松、零膨胀负二项、栅栏泊松、栅栏负二项4个模型拟合了大兴安岭地区每月林火发生频次和主要气象因子的相关关系。石晶晶[19]分别采用泊松、负二项、零膨胀泊松、零膨胀负二项回归4个模型拟合了浙江省龙泉市林火发生次数与主要气象因子的相关关系。Xiao等[20]分别采用泊松、负二项、零膨胀泊松、零膨胀负二项、栅栏泊松、栅栏负二项6个模型拟合了黔南布依族苗族自治州林火发生次数与主要气象因子的相关关系。

2 几种常用于林火发生预测的广义线性回归模型

广义线性模型是一般线性模型的扩展，它主要是通过连接函数ηi=f(μi)，建立响应变量Y的数学期望值与代表线性组合的预测变量P之间的关系。许多统计模型均属于广义线性模型，如Logistic回归模型、Probit回归模型、泊松分布回归模型、负二项分布回归模型等。用于预测森林火灾发生次数的广义线性模型主要包括正态分布回归模型、泊松分布回归模型、负二项分布回归模型、零膨胀模型、栅栏模型5种。其中，零膨胀模型又分为零膨胀泊松模型和零膨胀负二项模型，栅栏模型又分为Logit-Poisson栅栏模型和Logit-NB栅栏模型。

一个广义线性模型主要包括3个部分：①线性成分；②随机成分；③连接函数。

(1)

εi=Yi-ηi

(2)

ηi=g(μi)

(3)

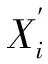
2.1 正态分布线性回归模型

正态分布线性回归模型就是指常用的传统线性回归模型。传统线性回归模型建立的前提条件是预测变量(或响应变量)服从正态分布，正态分布是概率统计中最重要的一种分布，也是自然界最常见的一种分布，正态分布的概率密度函数为：

(4)

式中：μ为总体的均值；σ为总体的标准差；χ为随机变量。

传统线性回归模型的公式如下：

(5)

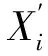
在传统线性回归模型中，只有预测变量(或响应变量)服从正态分布，预测变量的理论值服从正态分布，残差服从正态分布，模型的参数服从正态分布，才可构造出相应的服从一定分布的统计量(如F分布、t分布等)作假设检验，从而评价参数估计和模型拟合优度的优劣。

假定林火发生的次数服从正态分布，可直接以影响林火发生的因素(如降水量、相对湿度、风速、蒸发量、日照时数)为自变量，以林火发生的次数为因变量，建立多元线性回归模型进行预测。高颖仪等[21]建立了以长白山地区防火期内每日林火发生频次为因变量，以每日降水量、平均相对湿度、平均风速、日照时数、蒸发量为自变量的多元线性回归模型，并取得了一定的拟合优度(R2=0.768 6)。郭福涛等[17]建立了以大兴安岭地区每月林火发生频次为因变量，以每月平均风速、平均降水量、平均温度、平均相对湿度、平均蒸发量为自变量的多元回归模型，但是发现，模型拟合优度较差(R2≈0.2)。石晶晶[19]建立了以浙江省每月林火发生频次为因变量，以每月平均降水量、平均温度、平均相对湿度、平均风速为自变量的线性回归模型，拟合结果也显示，模型拟合优度较差(R2=0.024)。以上研究结果均表明，传统的线性回归模型不适于拟合林火发生次数与气象因子之间的相关关系。

2.2 Logistic广义线性回归模型

设随机变量yi服从参数为pi的二项分布：

则μi=E(yi)=pi，采用逻辑连接函数，即

(6)

式中：pi为发生某事件的概率；Xi和β分别为模型林火发生的自变量向量和参数向量。

Logistic广义线性模型常用于预测某单位林地发生森林火灾的概率。

2.3 泊松分布广义线性回归模型

传统多元回归模型预测林火发生次数精度较低的原因是因为林火发生次数并不服从正态分布，可能更趋近于泊松分布，泊松分布概率密度函数为：

(7)

式中：λ为随机变量y的均值；y为着火的次数。泊松分布的显著特点是期望与方差相等，均为λ。

Snedecor等[22]认为，用泊松回归模型预测每日人为森林火灾发生次数更为合理。Cunningham等[23]也认为，一个地区内每日人为森林火灾发生次数近似服从泊松分布。高颖仪等[21]通过统计长白山林区近20年来春秋防火期内每日林火发生频次，发现林火发生频次的平均值和方差基本相同，从而得出了当地林火发生频次基本符合泊松分布的结论。

与传统多元线性回归模型不同，泊松广义回归模型假定因变量(或响应变量)服从泊松分布，它是将因变量进行对数转换，通过连接函数与线性成分对接建立的一种模型。泊松广义线性回归模型为：

(8)

式中：μi为y的期望值，也等于λ；Xi和C分别为模型林火发生的自变量向量和参数向量；ln(μi)=ηi为连接函数。

郭福涛等[17]和孙龙等[24]分别建立的预测大兴安岭地区每月林火发生频次的泊松回归模型取得了比传统线性回归模型更高的拟合优度。石晶晶[19]也得到了同样的结果。

2.4 负二项分布广义线性回归模型

林火发生次数近似服从泊松分布的结论可能主要适用于林火发生次数的方差与均值近似相等，数据结构离散度较小的情况。如果统计林火发生的时间尺度延长(周、月等)，增加非防火期内发生的林火次数以及雷击火的发生次数，林火发生次数的方差可能大于均值，呈现过离散性结构。针对过度离散的数据，Gurmu等[25]认为采用负二项回归模型拟合效果更好。负二项分布概率密度函数为：

(9)

μ=r(1-p)/p

(10)

σ2=r(1-p)/p2

(11)

式中：p为伯努利试验中每次成功的概率；k为试验总次数；r为试验成功的次数；μ和σ分别为随机变量的期望和方差。从公式(9)和(10)可看出，负二项分布随机变量方差与期望比值大于1，其数据结构较泊松分布更为离散。因此，理论上，负二项广义线性回归模型在预测数据结构更为离散的林火发生次数的精度更高。

与泊松回归模型类似，负二项广义线性回归模型的连接函数为：ηi=ln(μi),只不过负二项回归模型多一个参数k，模型如下：

(12)

式中：μi为yi的期望值；Xi和B分别为模型的影响林火发生的自变量向量和参数向量；ln(μi)=ηi为连接函数。

Bruce[26]发现，美国路易斯安那州和密苏里州每日发生的林火次数服从二项分布。Symington[9]研究认为，运用负二项广义线性模型预测林火发生次数要比泊松模型更为精确。孙龙等[24]比较了泊松回归模型和负二项回归模型的拟合优度和预测大兴安岭地区每月林火发生次数的精度，结果显示，负二项回归模型优于泊松回归模型。石晶晶等[19]和Xiao等[20]也得到了相同的结论。

2.5 零膨胀模型(ZIP)

在统计每月或每日林火发生次数时，很多时候会出现林火发生次数为零的情况，造成这种情况有两个原因：第一，虽然有火源，但林内相对湿度、温度等因素不能使可燃物达到燃点；第二，可能因为随着防火宣传的深入，人们的防火意识大为增强，即使出现利于发生火灾的天气，但是没有火源。第一种情况出现的零为抽样零，可用泊松回归模型或负二项回归模型预测，第二种情况出现的零为结构零，不能用泊松回归模型或负二项回归模型预测，这也是导致零膨胀的原因，需用零膨胀模型来解决。

零膨胀模型假设随机变量出现的零数据包括结构零和抽样零，零数据概率也相应分为两个部分：结构零的概率pi可用二项分布概率密度函数计算；抽样零的概率可用泊松分布或负二项分布概率密度函数计算，随机变量出现零数据以外的所有数据的概率用泊松分布或负二项分布概率密度函数计算。零膨胀泊松分布和零膨胀负二项分布的概率密度函数分别为：

(13)

f(yi,λi,pi)=

(14)

式中：yi为林火发生次数；λi为服从泊松分布的随机变量yi的均值；pi为二项分布的概率；n为林火发生次数的最大值。

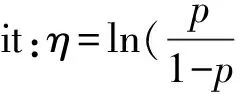
(15)

(16)

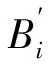
郭福涛等[17]比较了用于预测林火发生频次的泊松回归模型和零膨胀泊松模型的拟合优度，结果表明，零膨胀泊松模型的拟合优度和预测效果均优于泊松回归模型。秦凯伦等[18]比较了建立的零膨胀泊松模型和零膨胀负二项模型，发现零膨胀负二项模型的拟合效果和预测效果均优于零膨胀泊松模型。石晶晶[19]建立的泊松(Poisson)、负二项(NB)、零膨胀泊松(ZIP)、零膨胀负二项(ZINB)4个模型的拟合优度由强到弱的顺序为：ZINB>NB>ZIP>Poisson，预测效果由好到差的顺序为：ZINB>ZIP>NB>Poisson。Xiao等[20]建立的4个模型的拟合优度由强到弱的顺序为：NB>ZINB>ZIP>Poisson，其中，负二项回归模型的拟合优度略高于零膨胀负二项模型。

2.6 栅栏模型

栅栏模型将预测林火发生次数过程分为两步：第一步，决定是否发生林火，发生取值为“1”，未发生取值为“0”。若取值为1时，表示发生了林火，则模型运算跨越了栅栏进入第二阶段。与零膨胀模型不同，该模型认为，数据中的所有“0”均为结构零，即都因为没有火源。第一步中的“0”事件的连接函数有Logit和Probit两种，第二部分为典型零截尾形式的泊松分布或负二项分布[12]。栅栏模型表述如下：

f(yi|xi)=

(17)

式中：pi为发生林火为“0”次的概率；1-pi为跨越栅栏的概率，即发生林火的概率；f1(yi)/[1-f1(0)]表示零截尾的计数概率分布。将零截尾泊松分布和零截尾负二项分布表达式代入栅栏模型，得到如下泊松栅栏模型和负二项栅栏模型：

f(yi|xi)=

(18)

f(yi|xi)=

(19)

栅栏泊松模型认为，数据中的所有“0”均为结构零。但是一些地区的实际情况是：即使存在火源。由于林内可燃物含水率、空气相对湿度和温度等因素使林内可燃物达不到燃点，也不能发生林火，林火次数也为“0”。因此，栅栏模型的理论假设并不完全符合一些地区林火发生的实际情况，秦凯伦等[18]研究结果显示，建立的零膨胀泊松(ZIP)、零膨胀负二项(ZINB)、栅栏泊松(HP)、栅栏负二项(HNB)4个模型的拟合优度由强到弱的顺序为：ZINB>HNB>HP>ZIP，Xiao等[20]也得到了与之相同的结论。

3 广义线性模型的参数估计和假设检验

3.1 广义线性模型的参数估计

广义线性模型的参数估计一般不能用最小二乘法估计，常用加权最小二乘法或最大似然法估计。正态分布、泊松分布、负二项回归模型的对数似然表达式[3]分别为：

(20)

(21)

(22)

式中：Φ为离散系数；wi为离散权重；k为模型参数；yi和μi分别为因变量实测值和期望。

3.2 广义模型一些假设检验

广义模型的检验一般用似然比检验、Wald检验和记分检验，模型比较采用似然比检验。

3.2.1 回归系数的Wald检验

Wald检验是通过比较估计模型参数与“0”的差别来进行的，其检验统计量为：

(23)

3.2.2 模型拟合优度检验

1)赤池信息准则。

主要包括AIC、AICc、-2 Res Log Likelihood等，公式如下：

(24)

(25)

式中：l为对数似然值；k为被估计的参数个数。

-2 Res Log Likelihood为模型近似似然值的-2倍。AIC、AICc、-2 Res Log Likelihood值越小，表明模型拟合优度越高，反之，亦然。

2)似然比检验。

似然比检验主要是用于比较模型拟合效果的优劣。似然比检验的统计量G为：

G=-2×(lp-lk)

(26)

式中：lp和lk分别为模型P和模型K的对数似然函数。其中，模型P中的自变量是模型K中自变量的一部分，G服从自由度为K-P的χ2分布。

3)广义Pearsonχ2统计量。

(27)

4 结论与讨论

4.1 结 论

若把某地是否发生森林火灾看成一个随机变量，那么这个随机变量服从二项分布，随机变量的期望等于森林火灾发生的概率，预测森林火灾发生概率的最佳模型就是Logistic广义线性模型。

笔者讨论用于预测森林火灾发生次数的模型有传统多元线性、泊松、负二项、零膨胀泊松、零膨胀负二项、栅栏泊松和栅栏负二项7个模型。因为林火发生次数不是一个连续性变量，而是一个离散性变量，而且其数据结构一般不服从正态分布，因此，传统多元线性模型不适于预测林火发生次数。

林火发生次数近似服从泊松分布或负二项分布，到底服从两种分布中的哪一种，笔者认为，这主要取决于林火发生次数的数据结构，若林火发生次数的方差和期望相差不大，表明林火发生次数近似服从泊松分布，当林火发生次数的方差显著大于期望时，近似服从负二项分布。根据前人的研究显示，一般情况下，林火发生次数服从负二项分布。

某地一年中发生森林火灾的月份(或天数)很少，大部分为火灾次数为“0”的月份(或天数)，因此，通常会出现零膨胀现象，若单纯采用泊松分布或负二项分布都不能解释林火发生次数出现结构零的情况，需要采用零膨胀模型或栅栏模型。但由于栅栏模型的理论假设并不符合一些地区林火发生的实际情况，建议最好用零膨胀模型。如林火发生次数的方差和期望基本相等，应采用零膨胀泊松模型预测林火发生频次；当林火发生次数的方差显著大于期望时，应采用零膨胀负二项模型预测林火发生频次。一般情况下，零膨胀负二项模型预测林火发生频次的效果优于零膨胀泊松模型。

4.2 讨 论

1)为提高广义线性回归模型预测我国林火发生的精度，应增加模型变量。

除气象因子外，要全面、准确地预测林火发生的可能性和次数，还需考虑可燃物特征、地形、人类活动等因子。可燃物特征一般与所处的环境密切相关，包括可燃物类型、可燃物载量、可燃物组成、结构及可燃物含水率(包括细小可燃物含水率)等因素，可燃物越易燃，越容易引发森林火灾。同时地形因素、人类活动因子也与林火的发生有密切的关系。柳生吉等[27]分别采用广义线性模型和最大熵模型分析了地形、人类活动和土地覆被类型等环境因子对黑龙江省林火空间分布的影响，结果显示，地形因子和人类活动因子的作用较大。因此，为了提高模型精度，还需将可燃物特征、地形、人类活动等因子作为自变量引入建立的广义线性模型中。

根据前人研究显示，负二项分布模型或零膨胀负二项分布模型能更好地预测我国不同林区林火发生的概率和次数。尽管每个林区建立的模型都可能包含气象、可燃物特征、地形、人类活动等自变量因子，但是林区不同，模型自变量以及系数可能会存在差异，也即每个自变量对林火发生概率和次数影响可能不同。我国东北林区主要的地带性植被为温带针阔混交林和寒温带针叶林，针叶树种相对较多，以大兴安岭林区为例，仅兴安落叶松林面积就达到林区总面积的86.1%，兴安落叶松的总株数占大兴安岭所有树种总株数的72%。因此，与西南和东南两大林区相比，东北林区针叶树种所占比重对林火发生的影响可能更大，在林火发生模型中，体现为针叶树种所占比重因子的系数会较大。此外，与其他两大林区相比，东北林区尤其是大兴安岭是我国雷击火发生较多的地区，雷小丽等[28]研究发现大兴安岭地区每月或每日发生的森林雷击火与闪电具有较好的相关性，因此，在建立预测东北林区林火发生模型时，应将闪电次数作为自变量引入模型中。

与东北和东南林区相比，西南林区的地形因子和人类活动因子对森林火灾的影响更为显著。以云南省为例，该省山区面积占全省总面积的94%，辖区山峦起伏，山势陡峭，大部分地区海拔为1 500～2 000 m，气流易在山脉背风坡一侧形成焚风，从而易引发森林火灾。森林火灾还受海拔制约，每年发生在海拔1 600～3 000 m之间的火灾次数占全年总数的85%左右[29]。此外，西南地区是少数民族的聚居地，仅云南一省就有白族、傣族、水族、佤族、瑶族等20多个少数民族，这些少数民族依山而居，他们传统的耕作方式和独特的民俗用火习惯也易引发森林火灾。因此，与其他两大林区相比，地形和人类活动两个自变量因子对西南林区林火发生的影响可能更大。与西南林区和东北林区相比，东南林区交通便利，道路网密度较高，在预测东南林区林火发生模型中，距道路远近因子对林火发生的影响可能更大。

2)加大广义线性模型在区域性景观层次林火发生预报中的应用。

20世纪80年代以来，随景观生态学的兴起，促使林火干扰与森林的关系研究上升到景观尺度。林火直接影响森林斑块内部主要树种的分布比例并破坏廊道，同时，景观格局(斑块面积和类型、香农多样性指数、景观丰度等)对森林火灾也有一定影响。为了表达林火和森林景观之间的相互作用，很多景观模型被研建，如Dispatch、Embyr、Landis，这些模型均可预测林火发生及火场面积大小[30]。

国外的一些学者采用Logistic广义线性模型建立了基于景观尺度的林火发生概率模型[13-15]，而国内的相关研究很少。因此，可在我国的一些林区(或地区)开展相关的研究。通过采用Logistic广义线性模型建模方法，将研究区划分为若干个等面积的林地单元(边长至少大于10 m)，以海拔、坡向、坡度等地形因子，降雨量、平均风速、平均降雨量等气象因子，距离道路的远近、距离居住区的远近等人类活动因子，森林斑块大小、森林斑块形状等景观因子为自变量，可建立基于景观尺度的林火发生概率模型。

但是很少有学者建立基于景观尺度的林火发生次数模型。因此，通过将研究区划分为若干个等面积单元，采用负二项分布模型或零膨胀负二项分布模型的建模方法，可建立以气象因子、人类活动因子、地形因子和景观因子为自变量，以单位林地林火发生次数为因变量的广义线性模型。建立的模型不仅可精确地预测每个林地单元林火发生的概率，也能准确地估计林火发生的次数，从而便于为研究区森林火灾的预防和扑救提供决策。

3)拓展广义线性模型的建模方法。

目前，国内建立预测林火发生模型的方法是：①在一定时间段内，逐日(或月)统计同一研究区的各种气象因子和林火是否发生(或发生次数)并依次作为样本单元；②选取一部分样本，采用泊松分布、负二项分布等广义线性模型拟合不同样本气象因子和林火发生次数的相关关系，建立模型，并用另一部分样本验证模型精度。这种建模方法存在两个问题：①因为一些诸如地形和距道路距离、距居民点距离等人类活动因子基本不随时间发生改变，很难作为自变量加入到广义线性模型中。但是这些因子对林火的发生有很重要的作用，这就限制了模型的精度；②建立的广义线性模型尽管能够预测研究区林火发生的次数，但是一般研究区面积较大，火灾发生的具体区域不能确定，这为模型在研究区的应用带来一定的限制。

为了解决以上建模方法存在的问题，可将研究区划分为若干个正方形单元，根据火点发生的空间位置和时间，统计在每日(或月)每个单元中是否发生火灾或发生火灾的次数以及影响林火发生的气象、可燃物、地形、人类活动等各种因子，形成一系列纵向数据。以每日(或月)重复测量的同一单元为第一水平，以不同观测单元为第二水平，采用多层广义线性混合模型对纵向数据进行分析。第一水平的自变量以气象因子为主，第二水平的自变量可包括气象、可燃物、地形、人类活动等各种因子。这种实验和统计方法不仅能够提高模型预测林火发生的精度，也可进一步确定林火可能发生的具体区域，从而便于为研究区森林火灾预防提供决策支持。

此外，还可以采用广义相加模型的建模方法建立我国林火发生预测模型。广义线性模型要求自变量和因变量呈线性相关关系，但是并不是所有林火预测模型中的自变量与ln[pi/(1-pi)]呈线性相关关系，比如发生森林火灾的位置坐标、时间等自变量。广义相加模型是一种非参数模型，可为不与ln[pi/(1-pi)]呈线性相关关系的自变量建立相应的平滑函数并参与建模。这种模型也可较为精确地预测在研究区内何时何地可能发生森林火灾以及发生森林火灾的次数。

[1]舒立福, 张小罗, 戴兴安, 等. 林火研究综述(Ⅱ)林火预测预报[J]. 世界林业研究, 2003, 16(4):34-37. SHU L F, ZHANG X L, DAI X A, et al. Forest fire research(Ⅱ):fire forecast[J]. World Forestry Research, 2003, 16(4):34-37.

[2]NELDER J A, BAKER R J. Generalized linear models[J]. Journal of the Royal Statistical Society, Series A,1972, 135:370-384.

[3]McCULLAGH P, NELDER J A. Generalized linear models[M]. New York: Chapman and Hall, 1983.

[4]CROSBY J S. Probability of fire occurrence can be predicted[R]. USDA Forest Service, Central States Forest Experiment Station, 1954,143:14-15.

[5]DAYANANDA P W A. Stochastic models for forest fires[J]. Ecological Modelling, 1977, 3(4):309-313.

[6]WOTTON B M, MARTELL D L. A lightning fire occurrence model for Ontario[J]. Canadian Journal of Forest Research, 2005, 35(6):1389-1401.

[7]MANDALLAZ D, YE R. Prediction of forest fires with Poisson models[J]. Canadian Journal of Forest Research, 1997, 27(10):1685-1694.

[8]WOTTON B M, MARTELL D L, LOGAN K A. Climate change and people-caused forest fire occurrence in Ontario[J]. Climatic Change, 2003, 60(3):275-295.

[9]SYMINGTON P J. A Probabilistic model for predicting man-caused fire occurrence in Parry Sound,Ontario[D]. Toronto :University of Toronto, 1980.

[10]缪柏其, 韦剑, 宋卫国, 等. 林火数据的Logistic和零膨胀Poisson(ZIP)回归模型[J]. 火灾科学, 2008, 17(3):143-149. MIAO B Q, WEI J, SONG W G, et al. Logistic and ZIP regression model for forest fire data[J].Fire Safety Science,2008,17(3):143-149.

[11]VILAR L, WOOLFORD D G, MARTELL D L, et al. A model for predicting human-caused wildfire occurrence in the region of Madrid, Spain[J]. International Journal of Wildland Fire, 2010, 19(3):325-337.

[12]GUDMUNDSSON L, REGO F C, ROCHA M, et al. Predicting above normal wildfire activity in southern Europe as a function of meteorological drought[J]. Environmental Research Letters, 2014, 9(8):1-8.

[13]ALENCAR A A C, SOLRZANO L A, NEPSTAD D C. Modeling forest understory fires in an eastern Amazonian landscape[J]. Ecological Applications, 2004, 14(sp4):139-149.

[15]PREISLER H K, BRILLINGER D R, BURGAN R E, et al. Probability based models for estimation of wildfire risk[J]. International Journal of Wildland Fire, 2004, 13(2):133-142.

[16]郭福涛, 胡海清, 金森,等. 基于负二项和零膨胀负二项回归模型的大兴安岭地区雷击火与气象因素的关系[J]. 植物生态学报, 2010, 34(5):571-577. GUO F T, HU H Q, JIN S, et al. Relationship between forest lighting fire occurrence and weather factors in Daxing’an Mountains based on negative binomial model and zero-inflated negative binomial models[J]. Chinese Journal of Plant Ecology, 2010(5):571-577.

[17]郭福涛, 胡海清, 马志海, 等. 不同模型对拟合大兴安岭林火发生与气象因素关系的适用性[J]. 应用生态学报, 2010, 21(1):159-164. GUO F T, HU H Q, MA Z H, et al. Applicability of different models in simulating the relationships between forest fire occurrence and weather factors in Daxing’an Mountains[J]. Chinese Journal of Applied Ecology, 2010, 21(1):159-164.

[18]秦凯伦, 郭福涛, 邸雪颖, 等. 大兴安岭塔河地区林火发生的优势预测模型选择[J]. 应用生态学报, 2014, 25(3):731-737. QIN K L, GUO F T, DI X Y, et al. Selection of advantage prediction model for forest fire occurrence in Tahe, Daxing’an Mountain[J]. Chinese Journal of Applied Ecology, 2014, 25(3):731-737.

[19]石晶晶. 浙江省林火发生格局及预测模型研究[D]. 临安:浙江农林大学, 2014. SHI J J. Study on occurring space and forecasting model of forest fires in Zhejiang Province[D]. Lin’an: Zhejiang A & F Uni-versity, 2014.

[20]XIAO Y D, ZHANG X Q, JI P. Modeling forest fire occurrences using count-data mixed models in Qiannan Autonomous Prefecture of Guizhou Province in China[J]. PloS One, 2015, 10(3):1-12.

[21]高颖仪, 杨美和. 林火发生频次的动态数理模型[J]. 火灾科学, 1994, 3(2):7-13. GAO Y Y, YANG M H, TIAN N J. The dynamic mathematical model of forest-fire occurent frequency[J]. Fire Safety Science, 1994, 3(2):7-13.

[22]SNEDECOR G W, COCHRAN W G. Statistical methods[M]. Ames: The Iowa State University Press, 1967.

[23]CUNNINGHAM A A, MARTELL D L. A stochastic model for the occurrence of man-caused forest fires[J]. Canadian Journal of Forest Research, 1973, 3(2):282-287.

[24]孙龙, 尚喆超, 胡海清. Poisson回归模型和负二项回归模型在林火预测领域的应用[J]. 林业科学, 2012, 48(5):126-129. SUN L, SHANG Z C, HU H Q. Application of a poisson regression model and a negative binomial regression model in the forest fire forecasting[J]. Scientia Silvae Sinicae, 2012, 48(5):126-129.

[25]GURMU S, TRIVEDI P K. Excess zeros in count models for recreational trips[J]. Journal of Business & Economic Statistics, 1996, 14(4):469-477.

[26]BRUCE D. How many fires?[J]. Fire Control Notes, 1963, 24(2):45-50.

[27]柳生吉, 杨健. 基于广义线性模型和最大熵模型的黑龙江省林火空间分布模拟[J]. 生态学杂志, 2013, 32(6):1620-1628. LIU S J, YANG J. Modeling spatial patterns of forest fire in Heilongjiang Province using Generalized Linear Model and Maximum Entropy Model[J]. Chinese Journal of Ecology, 2013, 32(6):1620-1628.

[28]雷小丽, 周广胜, 贾丙瑞, 等. 大兴安岭地区森林雷击火与闪电的关系[J]. 应用生态学报, 2012, 23(7):1743-1750. LEI X L, ZHOU G S, JIA B R, et al. Relationships of forest fire with lightning in Daxing’anling Mountains, Northeast China[J]. Chinese Journal of Applied Ecology, 2012, 23(7):1743-1750.

[29]郑怀兵, 张南群, 方彦, 等. 云南省森林防火现状及对策研究[J]. 森林防火, 2007(4):19-22. ZHENG H B, ZHANG N Q, FANG Y, et al. Actuality and countermeasures on forest fire prevention in Yunnan Province[J]. Forest Fire Prevention, 2007(4):19-22.

[30]HE H S, MLADENOFF D J. Spatially explicit and stochastic simulation of forest-landscape fire disturbance and succession[J]. Ecology, 1999, 80(1):81-99.

Research on generalized linear models applied to forest fire forecast

ZHANG Jie1, ZHAO Haoyan1*, ZHANG Minxia1, LI Chenyang2, CHEN Geping1

(1.NanjingForestPoliceCollege,Nanjing210023,China;2.ForestFirePreventionMonitoringCenterofShanxiProvince,Taiyuan030012,China)

This paper firstly introduces the application of generalized linear models in forest fire forecast at home and abroad. Then the formulae, parametric estimation methods and hypothesis test methods of six forest-fire-forecasting models are introduced, including linear regression models, Logistic generalized linear models, Poisson generalized linear models, negative binomial generalized linear models, Zero-inflated generalized linear models and Hurdle generalized linear models. Logistic generalized linear models are mainly used for predicting the probability of forest fire occurrence and the other models are used for estimating the number of forest fireoccurrence. According to the characteristics of the forest fire frequency data and the previous relevant studies, it can be concluded that Poisson generalized linear models, negative binomial generalized linear models, Zero-inflated generalized linear models and Hurdle generalized linear models are more suited for estimating the number of forest fire than linear regression models. When the variance of the forest fire frequency is close to the expected value, Poisson generalized linear models or Zero-inflated Poisson generalized linear models can be successfully applied. If the variance of the forest fire frequency is significantly higher than the expected value, negative binomial generalized linear models and Zero-inflated negative binomial generalized linear models can better estimate the number of forest fire. Finally, suggestions are given on the application of the generalized linear models in forest fire forecast: firstly, more independent variables (the characteristics of forest fuel, terrain, human activities and other factors) should be added to established generalized linear models; secondly, the application for forest fire forecast in landscapes layer should be increased; thirdly, the modeling approaches of generalized linear models should be expanded (generalized linear mixed model and generalized additive models can be utilized).

generalized linear models; Poisson models; negative binomial models; Zero-inflated models; hurdle models

2015-12-14

2016-11-04

中央高校基本科研业务费专项资金项目(LGQN201402，LGYB201616)；南京森林警察学院教研教改项目(YB14118)。

张洁，女，副教授，研究方向为生态安全和土地利用变化。通信作者：赵浩彦，男，讲师。E-mail:469640903@qq.com

S762.3

A

2096-1359(2017)01-0135-08