双基地高频地波雷达模糊函数与克拉美罗界分析*

季志宇，吕 哲，于长军

(哈尔滨工业大学(威海) 信息与电气工程学院，山东 威海 264209)

双基地高频地波雷达模糊函数与克拉美罗界分析*

季志宇，吕 哲，于长军**

(哈尔滨工业大学(威海) 信息与电气工程学院，山东 威海 264209)

本文针对双基地体制下调频中断连续波(FMICW)信号的克拉美罗界问题，利用模糊函数和克拉美罗界之间的关系，给出了目标参数无偏估计的下界。仿真了双基地情况下波形参数对模糊函数形状的影响，以及站址和目标之间的几何构型与目标分辨能力之间的关系。分析表明，双基地雷达目标参数估计克拉美罗界取决于目标到达方向、基线长度以及目标与接收站之间的距离。最后根据克拉美罗界仿真分析了雷达双基地站址选择对目标估计精度的影响。

双基地雷达； 模糊函数； 参数估计； 克拉美-罗界

高频地波超视距雷达(HF Surface Wave Radar,HFSWR)是一种工作于3～30 MHz的高频段海上预警雷达[1]。系统多用调频中断连续波(Frequency Modulated Interrupted Continuous Wave,FMICW)，即脉冲截断的调频连续波信号作为发射波形，此种脉冲压缩波形既化解了距离分辨率和探测距离之间的矛盾又解决了发射和接收共址时的收发隔离问题。本文将分析采用FMICW信号的T-R双基地雷达系统的模糊函数及距离速度估计的克拉美-罗界(Cramer Rao Bound，CRB)。

模糊函数理论最初是为研究雷达分辨特性而提出，并从衡量两个不同距离、不同径向速度目标的分辨率出发给出了模糊函数的定义。它不仅可以分析雷达的分辨率，还可以用于分析测量精度、测量模糊度以及抗干扰性能等问题。文献[2]分析了高斯单脉冲和相干脉冲串体制下双基地雷达模糊函数及其特点，但该文献没有分析目标位置变化对目标参数估计精度的影响。文献[3]在文献[2]的基础利用网状架构模糊函数分析了多基地雷达与组网雷达的关键性能参数，证明了组网模糊度函数与网络中收发节点的相对位置和目标位置的相互关系。文献[4-5]都对双基地LFM脉冲信号模糊函数进行了研究，给出了目标双基地角与目标分辨率之间的关系表达式。而文献[6]针对调频连续波(Frequency Modulated Continuous Wave,FMCW)体制的双基地雷达模糊函数进行了建模，从模糊函数角度推导出了目标距离-速度参数估值及距离速度耦合斜率均受目标视角的影响。

对于参数估计问题，CRB给出了无偏估计量下限，它做为一个标准，常用于雷达目标参数的估计当中[7-9]。借鉴这一思想，本文将克拉美-罗界用于双基地高频地波雷达的目标距离-速度参数联合估计当中，首先推导了T-R型双基地FMICW雷达信号模糊函数，借助Fisher信息矩阵(Fisher Information Matrix，FIM)给出了双基地HFSWR的CRB形式，定量描述了双基地高频地波雷达目标参数无偏估计量的下界。仿真分析了雷达双基地站址选择与目标位置双重参量对目标的速度-距离联合估计精度与目标分辨能力的影响。

1 双基地FMICW雷达信号模糊函数

为推导T-R型双基地高频雷达FMICW信号的模糊函数，首先建立如图1所示的结构模型[10]。整个雷达系统由发射站T、接收站R和机动目标Tgt构成，其中RT为目标到发射站的距离，RR为目标到接收站的距离，L为基线长度，V为机动目标的运动速度。

图1 T-R型双基地雷达结构图

对于通常的单基地T/R雷达慢起伏点模型，由模糊函数的定义式我们可得

(1)

由于雷达采用FMICW作为发射波形，其信号形式如式(2)所示。

(2)

那么将f(t)与时延为τ的回波信号f(t+τ)表达式均代入式(1)中可以得到单基地T/R雷达FMICW信号的模糊函数表达式如式(3)所示。

(3)

经过整理可得

(4)

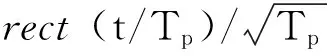
(5)

将式(5)代入式(4)中，可以得到T/R雷达模糊函数表达式最终形式如式(6)所示。

(6)

令fd=0，可得距离模糊函数如式(7)所示。

(7)

以距离模糊函数主瓣第一次过零点τ值定义距离分辨率[10]，由式(7)可得，主瓣宽度主要由1/μNTr决定，又因为带宽Bn=μNTr，表明距离分辨率与调频带宽Bn成反比。

令τ=0，可得多普勒模糊函数如式(8)所示。

(8)

同样的，以多普勒模糊函数主瓣第一次过零点fd值定义多普勒分辨率，从式(8)可得，主瓣宽度近似等于1/NTr，即多普勒分辨率与相干积累时间成反比。

对于T-R双基地雷达的模糊函数，由于目标到接收站与目标至发射站不再是同一条路径，因此要对式(6)做出适当修正。假设有两个目标Tgt1和Tgt2，回波时延和多普勒频移分别为(τ1fd1)和(τ2,fd2)，以接收站为参考点，目标Tgt1的(τ1fd1)为已知目标时，分析双基地雷达对Tgt1和Tgt2的分辨能力。由下列公式计算两个目标的回波时延和多普勒频移：

(9)

(10)

(11)

其中，β为双基地角，将回波时延差Δτ=τ2-τ1和多普勒频移差Δfd=fd2-fd1，代替T/R雷达模糊度函数中的τ和fd，得到T-R双基地雷达发射FMICW信号时的模糊函数表达式为：

(12)

可以看出，该模糊函数的形式是关于双基地角的函数，说明其分辨率不仅与信号形式有关，而且还受目标位置影响[11]。对于图1所示双基地雷达，根据表1所示参数，仿真其距离模糊函数与目标视角θR之间关系，当θR分别取20°与60°时的仿真结果如图2所示。由仿真结果可见，距离模糊函数主瓣宽度随θR的增加而展宽，即当目标靠近基线时，目标分辨率显著降低。

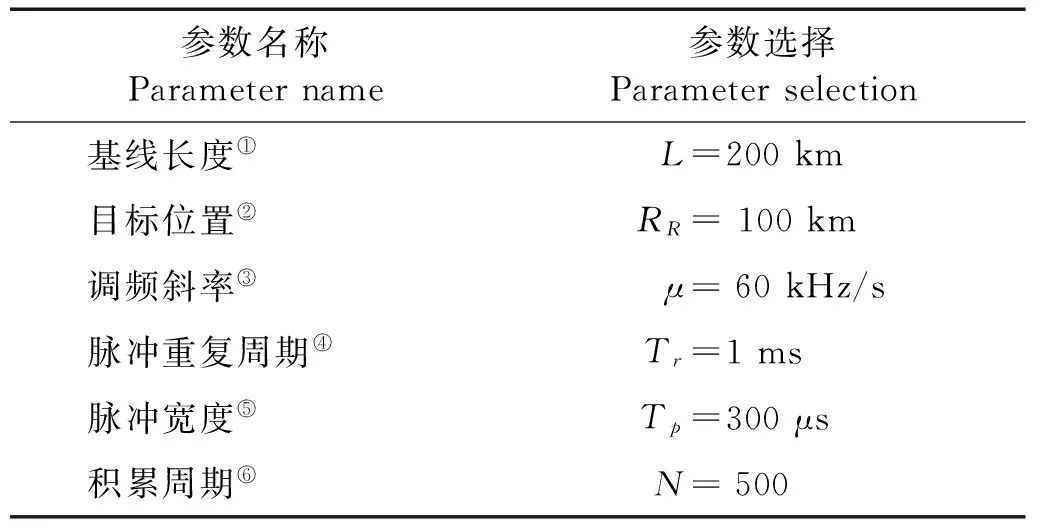
表1 双基地雷达仿真参数

Note：①Baselinelength；②Targetposition；③Frequencymodulatedslope；④Pulserepetitioninterval；⑤duration；⑥Accumulationperiod

2 距离-速度联合估计CRLB

由上节分析可知，模糊度函数表示雷达距离-速度联合估计的分辨能力，而克拉美-罗下界(CramerRaoLowBound，CRLB)定义的是无偏估计量方差的下界，是理论上双基地雷达测量精度的最优值，为雷达的探测性能评估提供了判断依据。克拉美-罗下界的计算基于模糊度函数[12]，为了得到T-R配置下双基地高频地波雷达距离-速度联合分辨CRLB，首先给出T/R单基地高频地波雷达模糊度函数的Fisher信息矩阵(FisherInformationMatrix，FIM)如式(13)所示。

图2 不同目标视角下的距离模糊函数Fig.2 Distance ambiguity function with different target angle

(13)

(14)

(15)

再考虑T-R型双基地配置下的FIM。根据式(9)～(11)可知，τ=τ(RR)和fd=fd(RR,V)是关于(RR,V)的函数，因此T-R型双基地雷达的FIM可以表示为

(16)

再根据函数链式求导法则，可以得到式(17)～(19)。

(17)

(18)

(19)

由式(9)～(11)我们可以得到τ与fd对V、RR的各阶偏导数，但速度V不是回波时延τ的函数，因此

(20)

(21)

(22)

(23)

再将式(21)～(23)带回到式(16)即可得T-R型双基地高频地波雷达距离-速度联合估计的CRLB，如式(24)、(25)所示。

(24)

(25)

现仿真分析T-R配置下的双基地高频地波雷达距离-速度联合估计CRLB随基线长度变化情况。仿真参数如表2所示。以T站为坐标原点建立直角坐标系(单位：km)，目标位置固定在(20,20)保持不变，基线长度L在[0,200km]范围内变化时，仿真结果如图3所示。

表2 双基地雷达仿真参数

Note：①Operatingfrequency；②Signalbandwidth；③Pulserepetitioninterval；④Pulseduration；⑤SNR；⑥Accumulationperiod

由图3a所示，虚线代表了单基地T/R配置下的CRLB曲线，即理想条件下双基地雷达可以达到的最优精度。T-R双基地高频地波雷达的距离估计精度随着基线长度的增大越来越差，在基线长度小于20km时，双基地CRLB曲线与单基地CRLB曲线基本重合，此时估计精度很高。因此在收/发两站位置相距较远时，是以牺牲探测精度为代价，换取了探测距离的延伸。由图3b所示，双基地高频地波雷达速度估计的CRLB曲线与距离维估值的趋势基本相同，随着基线长度的增加，速度估计精度下降，在基线长度小于10km左右时，双基地雷达速度测量精度较高。

假设基线长度L=200 km固定，其它仿真参数不变，当接收站R测得的目标视角θR在[-π,π]范围内变化时，仿真T-R型双基地雷达距离-速度联合估计CRLB随接收站视角的变化趋势如图4所示。

由图4可以看出，距离-速度估值的CRLB曲线类似于一个冲激函数，在θR=-90°左右时，目标参数估计精度非常差。此时目标处于基线附近，目标到发射站与接收站的距离和约等于基线长度，R站所测得的回波时延τ=L/c变为固定值，致使雷达目标定位能力变差。如果两目标正位于基线上，且移动速度也相等，那么T-R配置下的双基地雷达甚至无法区分这两个目标。

图3 不同基线长度CRLB曲线

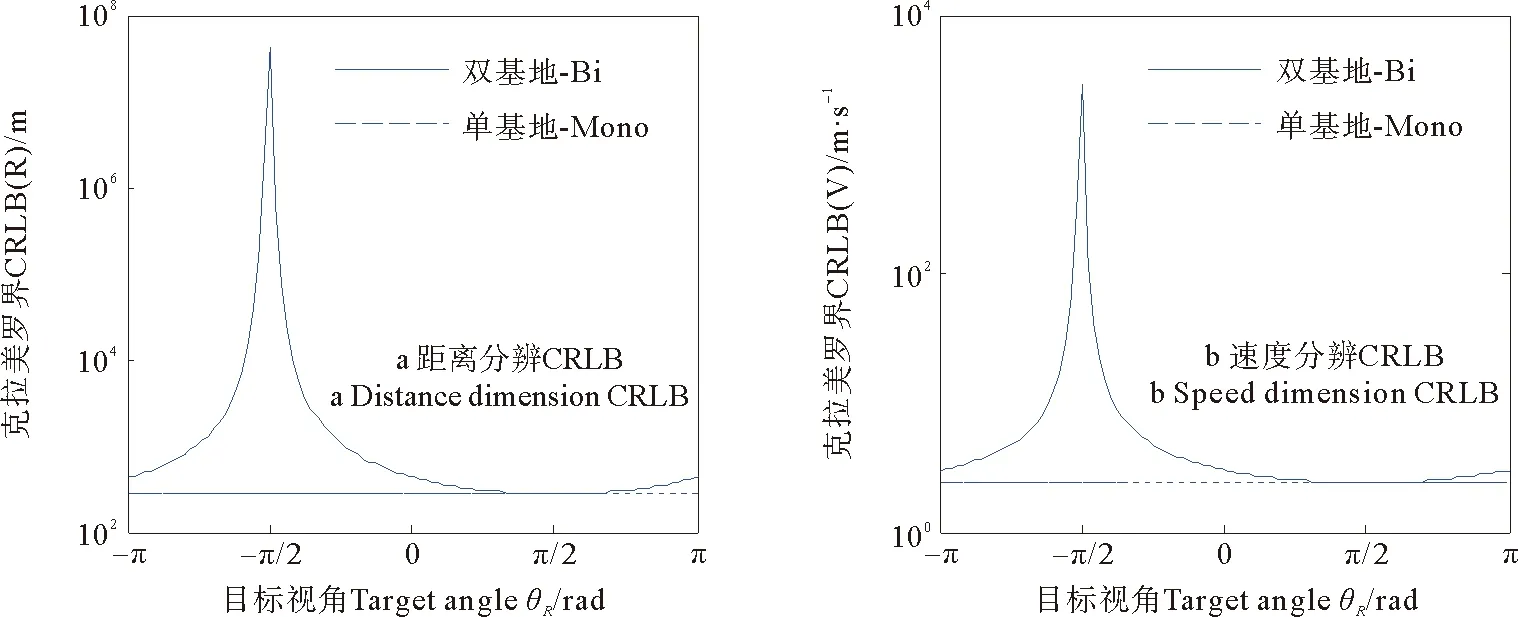
图4 不同目标视角CRLB曲线Fig.4 CRLB as function of target angle

3 双基地站址选择

雷达的作用距离与估值精度是衡量雷达性能的两个重要指标，它的大小不仅取决于雷达系统参数，目标特性及环境因素也会对雷达性能产生影响[13]。回波信噪比作为探测目标的重要衡量参数，极大程度的影响着双基地雷达的探测性能，通过仿真及大量实验表明回波信噪比为14dB时目标的发现概率约为90%，漏警概率约为10-6。图5为回波信噪比与双基地雷达探测范围示意图。

由图5所示，当SNR达到临界值14dB时，最大探测范围为双纽线，当SNR变大时，最大探测范围为一条卵形线。

由前文分析可知，双基地雷达测距测速精度与基线长度即收/发站址几何位置有关，同时基线长度也影响着双基地雷达探测范围。现令回波信噪比SNR= 14dB、双基地雷达工作频率fc= 11 MHz 固定不变，目标的运动范围为400 km×400 km的矩形区域，基线长度L分别取L=160、200和240 km时得到不同基线长度下对应的每个目标位置的距离-速度CRLB，经过归一化处理之后的估值误差分布如图6所示。

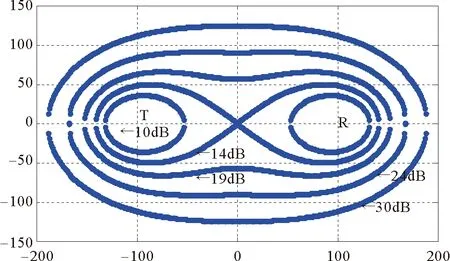
图5 信噪比与探测范围示意图Fig.5 The schematic diagram of SNR on the detection range

由图6可见，距离估值和速度估值精度分布情况大致相近，整体趋势成梭形分布；基线及基线附近区域的距离速度估值精度较差，T站和R站附近距离速度估值较好，目标距离收/发两站越远，测距测速的性能越差。对比三种基线长度下的估值误差分布，选择较小的基线长度时，可以保证双基地雷达距离速度估计的准确性；随着基线长度不断增大，以探测精度下降换取探测范围的扩展。所以在双基地雷达布站时，应综合考虑各方面因素，才能确定满足系统需求下的双基地站址几何位置布局。该结论可以用于雷达建模理论分析与雷达探测性能评估当中，同时也可以为FMICW信号体制的双基地雷达布站与优化提供理论依据。

图6 不同目标位置估值误差示意图Fig.6 Estimate deviation with different target position

4 结语

本文在T-R型双基地高频地波雷达FMICW信号模糊函数的基础上，利用模糊度函数平方的偏导数构成FIM，进而得到距离-速度估值的CRLB。分析了基线长度与目标视角对CRLB的影响，并以CRLB为参考指标，仿真了在不同基线长度布站下的雷达性能。在此基础上可将该方法引入组网雷达系统中，计算网络中每一组T站与R站间的CRLB，并将其作为参考标准用于组网雷达系统各区域最佳发射-接收组合的选取当中，使组网雷达整体探测效果得到提升。

[1] Trizna D B.A bistatic HF radar for current mapping and robust ship tracking[J].Sea Technology，2008，50(6)：1-6.

[2] Tsao T，Slamani M，Varshney P，et al.Ambiguity function for a bistatic radar[J].IEEE Transactions on Aerospace & Electronic Systems，1997，33(3)：1041-1051.

[3] Papoutsis I，Baker C J，Griffiths H D.Netted radar and the ambiguity function[C].Radar Conference：2005 IEEE International.2005：883-888.

[4] 花汉兵.双基地LFM雷达信号模糊函数研究[J].现代电子技术，2010，13：21-23.Hua Han-bing.Study of ambiguity function for bistatic LFM radar signal[J].Modern Electronics Technique，2010，13：21-23.

[5] 战立晓，汤子跃，朱振波.基于模糊函数的双基地雷达LFM脉冲信号分辨特性研究[J].武汉理工大学学报(交通科学与工程版)，2011，35(6)：1284-1288.Zhan Li-xiao，Tang Zi-yue，Zhu Zhen-bo.Study on the resolution of LFM pulse signal for a bistatic radar based on ambiguity function[J].Journal of Wuhan University of Technology(Transportation Science & Engineering)，2011，35(6)：1284-1288.

[6] 张容权,黄钰林,杨建宇.双基地线性FMCW雷达信号模糊函数及分辨特性[J].电子与信息学报，2007，29(4)：836-840.Zhang Rong-quan，Huang Yu-lin，Yang Jian-yu.Ambiguity function and resolution characteristic of bistatic linear FMCW radar signal[J].Journal of Electronics & Information Technology，2007，29(4)：836-840.

[7] Lee Y K，Yang S H，Lee C B，et al.Evaluation of performance enhancement on CRLB of CAF under multiple emitters [J].Electronics Letters，2015,52(3):235-237.

[8] Kumarasiri R，Alshamaileh K，Tran N H，et al.An improved hybrid RSS/TDOA wireless sensors localization technique utilizing Wi-Fi networks[J].Mobile Networks & Applications，2015，21(2)：1-10.

[9] Kaune R.Accuracy studies for TDOA and TOA localization[C].Singapore:International Conference on Information Fusion.2012：408-415.

[10] 花汉兵，王建新.调频中断连续波雷达信号模糊函数及其分辨特性[J].南京理工大学学报，2012，36(1)：101-105.Hua Han-Bing，Wang Jian-Xi.Ambiguity function and resolution characteristics of FMICW radar signal[J].Journal of Nanjing University of Science and Technology，2012，36(1)：101-105.

[11] 陈多芳，陈伯孝，刘春波，等.岸一舰双基地SIAR雷达距离一速度分辨率分析[J].系统工程与电子技术，2008，30(1)：75-78.Chen Duo-fang，Chen Bai-xiao，Liu Chun—bo，et al.Analysis of range-velocity resolution for coast-ship bistatic SIAR [J].Systems Engineering and Electronics，2008，30(1)：75-78.

[12] Greco M S，Stinco P，Gini F，et al.Cramer-rao bounds and selection of bistatic channels for multistatic radar systems[J].IEEE Transactions on Aerospace & Electronic Systems，2011，47(4)：2934-2948.

[13] 何缓，柯亨玉，万显荣，等.双基地高频地波雷达系统布站研究[J].电子与信息学报，2012，34(2)：333-337.He Huan，Ke Heng-yu，Wan Xian-rong，et al.Study on the distribution of bistatic high-frequency ground wave radar system[J].Journal of Electronics & Information Technology，2012，34(2)：333-337.

责任编辑 陈呈超

Cramer Rao Bound Analysis and Ambiguity Function of Bistatic High Frequency Surface Wave Radar

JI Zhi-Yu，LV Zhe，YU Chang-Jun

(School of Information and Electronic Engineering,Harbin Institute of Technology (Weihai),Weihai 264209,China )

In this paper we deal with the problem of the Cramer Rao bounds for bistatic radar with FMICW signal.The lower bound of the parameter unbiased estimate is delimited by exploiting the relation between the ambiguity function and the Cramer Rao bounds.In the bistatic case,this paper analyze the impact on the shape of the ambiguity function by the waveform parameter and the relation between the geometry factors and the ability to distinguish target.The analysis shows the Cramer Rao bounds depend on the target direction of arrival,the bistatic baseline length and the distance between the target and the receiver.The Cramer Rao bounds are then used to analyze the impact on the target estimation accuracy by the choice of station site in bistatic radar.

bistatic radar;ambiguity function;parameter estimation;CRB

国家自然科学基金项目(61571159)；海洋公益性行业科研专项(201505002)资助

Supported by the National Natural Science Fund Project of China(61571159)；The Public Science and Technology Research Funds Projects of Ocean(201505002)

2016-09-15;

2016-11-26

季志宇(1993-)，男，硕士生。E-mail:jizhiyu.ahu@sohu.com

** 通讯作者：E-mail:yuchangjun@hit_edu_cn

TN958

A

1672-5174(2017)02-037-07

10.16441/j.cnki.hdxb.20160283

季志宇，吕哲，于长军.双基地高频地波雷达模糊函数与克拉美罗界分析[J].中国海洋大学学报(自然科学版),2017,47(2):37-43.

JI Zhi-Yu，LV Zhe，YU Chang-Jun.Cramer rao bound analysis and ambiguity function of bistatic high frequency surface wave radar[J].Periodical of Ocean University of China,2017,47(2):37-43.