一种阵列式高频地波雷达比幅测向新方法*

张 玲，刘 旭，姜 義，牛 炯

(中国海洋大学工程学院，山东省高校海洋机电装备与仪器重点实验室,山东 青岛 266100)

一种阵列式高频地波雷达比幅测向新方法*

张 玲，刘 旭，姜 義，牛 炯

(中国海洋大学工程学院，山东省高校海洋机电装备与仪器重点实验室,山东 青岛 266100)

高频地波雷达的精确测向是该领域的难题，现有测向方法存在测向不准确、运算量较大等问题。本文对阵列式高频地波雷达比幅测向的公式进行了推导，得出了比幅测向定理。区别于传统的比幅测向方法，本文方法没有用高斯函数近似方向图，而是在真实方向图基础上推导得出了测向新方法，该方法能够从数学上给出各个方位的精确解。用这两种方法对模拟来波数据和高频地波雷达实测数据进行测向分析，并将实测数据测向结果与合作船只的同步实测自动识别系统(AIS)数据比较分析，结果表明本文方法测向误差更小，验证了本文方法的有效性。

阵列信号处理； 高频地波雷达； 比幅； 波束合成

高频地波雷达具有可全天候工作、超视距探测等优点，因此在监测专属经济区、保护海洋环境等方面得到了越来越广泛的应用[1-2]。但是由于该雷达波长比较长，对目标的方位不敏感，导致目标测向(Direction Finding,DF)精度比较低，由此使得高频地波雷达目标精确定位和跟踪较为困难。由于高频地波雷达探测的目标距离较远，达到300 km以上，所以即使测向角度误差为1°时，也会造成几十千米以上的定位偏差。所以如何实现精确测向成为了高频地波雷达目标跟踪的重要研究问题[3]。

现有的地波雷达测向方法包括数字波束合成法(DBF)、MUSIC方法、比幅测向方法等[4-6]。比幅测向方法是一种常用的基于波束合成的测向方法，现有的比幅测向方法大多是将方向图函数近似为高斯函数，或者假设不同波束中心指向的方向图是完全一样的[7-9],在此假设的基础上通过公式推导得出目标来波的求解公式。通过分析实际的阵列式地波雷达的方向图发现以上假设和近似与实际情况不完全一致，由此导致测向结果始终存在一定误差，限制了该方法的应用。

本文的新方法没有使用高斯函数近似方向图，也没有假定不同波束中心指向的方向图完全一样，而是在真实方向图基础上进行公式推导，求出了目标角度、相邻波束角度和来波幅度比值满足的方程式，并总结为比幅测向定理。该方法能够从数学上给出来波角度的精确计算方法，并且以该定理为核心建立了一套新的测向方法。

1 比幅测向原理

阵列式高频地波雷达在窄带条件下，导向矢量为

其中：α为目标方位角；λ为波长；d为阵元间距；N为阵元个数。经过DBF处理后的输出为

其中：w1为复加权矢量；T表示转置；B为切比雪夫加权矩阵，可以增强方向图主瓣抑制旁瓣。

w1=w1(θ)，θ可以以一定扫描精度遍历雷达测向的角度范围，当θ与α差值最小时，输出y最大。这就是DBF法测向的基本原理。但该方法运算量较大，且测向精度依赖扫描精度，因此考虑用目标附近的邻近波束比值来确定目标方向，即比幅法测向。

以多个波束对地波雷达回波数据作DBF处理后，在来波方向取2个相邻波束的方向图的最大和次大值(见图1)，在-13°和0°对应的波束上分别取得了最大和次大值。这2个相邻波束的角度是已知的，可得其功率比

其中θ1和θ2为已知的相邻波束的角度。

图1 比幅测向原理示意图

如何利用已知的相邻波束的角度和功率比求目标方位是比幅测向处理的核心问题[10-11]。传统比幅测向多是将方向图作近似处理，例如近似为高斯函数y(θ)=e-kθ2，在此基础上通过公式推导求得目标方位公式。高斯函数的近似方向图见图2。

图2 高斯函数近似方向图

从图2可以看出，不同波束中心指向的方向图形状并不完全一样，高斯函数近似的方向图始终与真实方向图存在一定偏差。这说明传统比幅测向方法的假设与实际情况并不完全一致，这导致了传统比幅测向方法得出的测向结果始终存在误差。而本文方法在真实方向图基础上进行严格的公式推导，得出了如下比幅测向定理。

2 比幅测向定理

(pATC-AT)X(x)-pATDY(x)=0，

(1)

α=arcsin(x+sin(θ1))，

(2)

其中，由已知的雷达参数可以直接求得的方程参数为

(3)

m=sin(θ1)-sin(θ2)，

(4)

(5)

(6)

(7)

(8)

包含未知量的变量为

x=sin(α)-sin(θ1)，

(9)

(10)

(11)

定理证明：

设相邻波束的两个复数权矢量为

w1=

w2=

其中,H表示共轭转置。

则

(12)

利用欧拉公式aeiθ=acos(θ)+iasin(θ)代入公式(12)得

求平方得

⋮+

bN-2bN-1cos((N-2)kx-(N-1)kx)]整理上式，得

2(b0b1+b1b2+ … +bN-2bN-1)cos(kx) +

2(b0b2+b1b3+ … +bN-3bN-1)cos(2kx) +…+

2b0bN-1cos((N-1)kx),

写成矩阵形式，设

则

同理可得

其中

将X2展开，设

得X2=(CX(x)-DY(x))

所以(pATC-AT)X(x)-pATDY(x)=0。

又因为x=sin(α)-sin(θ1)，可求得来波方向α=arcsin(x+sin(θ1))。

定理得证。

3 方法流程

本文方法完整的流程见图3。

第一步。输入的是目标点的多通道数据，是一个列向量，其维数等于阵元个数。

第二步。用DBF法采用加权方式处理多通道数据。

第三步。对处理结果排序，求得最大和次大值对应的波束角度，并求出最大和次大值的幅度比值。第四步。将第三步结果和雷达阵元间距、电磁波频率等参数代入公式(3)～(8)，根据公式(9)～(11)设未知量。第五步。将第三步结果代入公式(1)、(2)求得目标来波方向。

4 方法验证

4.1 模拟数据仿真

本文雷达系统采用八阵元天线阵列，阵元间距d为14.5m,频率f为4.7MHz。来波方向在-48°到48°之间随机模拟。利用雷达阵列接收信号模型模拟雷达接收数据，用本文方法和文献[6]中传统的比幅测向方法分别测向。表1中本文方法误差均值为0°，方差为0，传统比幅方法的误差均值为2.63°，方差为4.17。可以看出对于模拟来波数据，本文方法能够精确求出来波方向，而传统的比幅测向方法求出的来波方向存在一定误差，仿真结果表明了本文提出的比幅测向新方法相比于传统的比幅测向方法具有更高的准确性。

4.2 实测数据测向与AIS验证

船舶自动识别系统(AutomaticIdentificationSystem)简称AIS，由岸基(基站)设施和船载设备共同组成，其配合全球定位系统(GPS)能提供船位、船速、转向率及航向等船舶动态信息，可以用来验证雷达目标测向的准确性[10]。

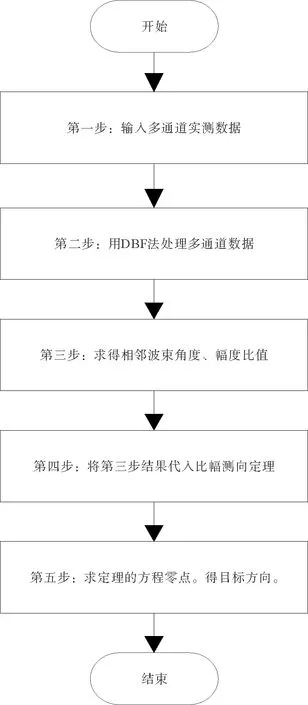
图3 比幅测向流程图

模拟来波方向/(°)SimulatedDOA(angle)测向结果/(°)DFresults误差分析Erroranalysis本文方法Newmethod传统比幅法Traditionalmethod本文方法Newmethod传统比幅法Traditionalmethod23.45223.45220.48202.97-20.089-20.089-19.32700.762-37.193-37.193-31.94105.252-40.963-40.963-45.74704.7843.9833.9834.49300.5147.13047.1345.61201.518

用同一时段的高频地波雷达回波数据和AIS数据进行匹配，首先是利用AIS数据求出船只目标的真实距离和径向速度，并将其投射到雷达回波数据的距离多普勒(RD)谱上(见图4)。

图4 AIS与地波雷达数据的匹配RD谱图

图4中被圈出的是AIS结果，当被圈出的点同时是深色目标点时，AIS与雷达数据同时报告该处有目标船只，实现了相互匹配。从图4中可以看出RD谱中某些极大值没有AIS数据对应，当某些船只关闭了AIS时，会导致这种情况的出现。匹配结果的目标点坐标见表2。

表2 AIS与地波雷达匹配目标点坐标

然后计算该点AIS方位信息，并用本文方法和文献[6]中传统的比幅测向方法分别处理雷达数据，求得方位信息。并将结果与AIS方位信息进行对比，求得两种方法的测向误差，结果见表3。

表3中本文方法测向误差均值为1.25°，方差为0.80，传统比幅测向方法误差均值为2.63°，方差为6.96。测向结果再次表明本文方法具有更高的准确性和稳定性。本文方法对实测数据的处理结果存在误差，误差的产生是多方面的，一方面是AIS的结果并不完全准确，其本身存在一定误差。另一方面，雷达回波数据由于受到电离层杂波、射频干扰等因素的影响，其回波强度会有一定误差，而比幅测向对回波强度的准确性要求较高，所以会造成一定误差[11-14]。该结果表明本文方法在处理高频地波雷达实测数据时具有较高的准确度。

表3 AIS与两种测向方法对比Table 3 Comparison of AIS and the two direction finding methods

5 结语

本文通过公式推导得出了阵列式高频地波雷达比幅测向的新方法。对模拟来波数据的仿真结果表明，本文方法能够精确求得来波方向，比传统的比幅测向方法具有更高准确性。对某批次的地波雷达实测数据的测向结果表明，本文方法的测向误差均值为1.25°，比传统比幅方法减小了1.38°，本文方法的测向误差的方差为0.80，比传统方法减小了6.16。实测数据验证结果表明，本文方法求得的方位与AIS方位误差更小，比传统的比幅测向方法准确性和稳定性更高。另外，地波雷达实测数据受到了杂波干扰等因素的影响，以及AIS数据本身的误差，导致了本文方法对实测数据的测向结果存在误差。如何减小对实测数据的测向误差，是下一步的工作。

[1]GuinvarcHR,GillardR,UguenB,etal.ImprovingtheazimuthalresolutionofHFSWRwithmultiplicativebeamforming[J].IEEEGeoscience&RemoteSensingLetters,2012,9(5):925-927.

[2]WangW,GillEW.EvaluationofBeamformingandDirectionFindingforaPhasedArrayHFOceanCurrentRadar[C].Dresden:InternationalRadarSymposium,2013:417-422.

[3]WangZ,XieJ,ZhouG,etal.Real-valuedsparserepresentationforsinglesnapshotdirection-of-arrivalestimationinshipbornehigh-frequencysurfacewaveradar[J].IetRadarSonarNavigation,2015,9(9):1314-1322.

[4]TuanDH,PeterR.Signalprocessingforwidebandsmartantennaarrayapplication[J].IEEEMicrowaveMagazine,2004,5(1):57-67.

[5]NordeboS,ClaessonI,NordholmS.WeightedChebyshevapproximationforthedesignofbroadbandbeamformersusingquadraticprogramming[J].IEEESignalProcessingLett,1994,1(7):103-105.

[6] 马银玲,毛秀丽.基于DBF的比幅测向方法研究[J].舰船电子对抗,2014,37(2):91-93.MaYL,MaoXL.ResearchintoamplitudecomparisonDFmethodbasedonDBF[J].ShipboardElectronicCountermeasure,2014,37(2):91-93.

[7] 顾敏剑.多波束比幅测向系统精度分析[J].舰船电子对抗,2007,30(3):70-73.GuMJ.AccuracyanalysisonMulti-beamamplitude-comparisonDirectionFindingsystem[J].ShipboardElectronicCountermeasure,2007,30(3):70-73.

[8] 翟庆伟,王玉,宫兵.波束比幅法测向技术研究[J].无线电通信技术,2007,33(6):55-56.ZhaiQW,WangY,GongB.ResearchonthetechnologyofthebeamamplitudecomparisonDirectionFinding[J],RadioCommunicationsTechnology,2007,33(6):55-56.

[9] 唐庆乐.高频地波雷达舰船目标探测方位向估计与修正[D].青岛：中国石油大学(华东)信息与控制工程学院,2013：8-17.TangQL.ShipDetectionDirectionFindingandRectificationforHFSWR[D].QingDao:CollegeofInformation&ControlEngineering,ChinaUniversityofPetroleum(EastChina),2013：8-17.

[10]GurgelKW,SchlickT,HorstmannJ,etal.EvaluationofanHF-radarshipdetectionandtrackingalgorithmbycomparisontoAISandSARdata[C].IEEE,WatersideSecurityEonference(WSS).Carrara:IEEE,2010:1-6.

[11]CooperDC,LongstaffID.Errorscausedbyclutterinamplitude-comparisonDirectionDindingsystems[J].IETJournals&Magazines，1972,119(3):305-311.

[12]ZhouH,WenB,WuS.IonosphericcluttersuppressioninHFSWRusingmultilayercrossed-Loopantennas[J].IEEEGeoscienceandRemoteSensingLetters,2014,11(2):429-433.

[13]JohnW,WeiminH,EricW.AnanalyticalmodelforHFradarionosphericclutter[J].AntennasandPropagationSocietyInternationalSymposium(APSURSI),2013IEEE,2013,1974-1975.

[14]RavanM,AdveRS.IonosphericClutterModelforHighFrequencySurfaceWaveRadar[C].Atlanta:RadarConference(RADAR),2012IEEE,2012:377-382.

责任编辑 陈呈超

A Novel Amplitude Comparison Direction Finding Algorithm for Array HFSWR

ZHANG Ling,LIU Xu,JIANG Yi，NIU Jiong

(1.College of Engineering,Ocean University of China,Key Laboratory of Marine Mechanical and Electrical Equipment & Instruments of Shandong Provincial Universities,Qingdao 266100,China)

The precise direction finding for high frequency surface wave radar (HFSWR) is a difficult problem.The conventional methods of direction finding have several problems,such as inaccuracy of direction finding,lower computation efficiency.In this paper,an amplitude comparison theorem based on the amplitude comparison formula of array HFSWR is derived.The proposed method does not use the approximate pattern of Gaussian function but the real pattem,which is different from the traditional amplitude comparison method.The proposed method can give the exact solution of arbitrary azimuth of the target.Both the new algorithm and the traditional one are applied to process the simulation data to show the effectiveness by analyzing the direction finding results.It shows that the proposed algorithm is more accurate compared with traditional methods.Moreover,the field experiment results demonstrate that the proposed method performs better than the conventional method in terms of direction finding accuracy by processing the HFSWR measured data based on the cooperative vessels’ AIS information.

array signal processing; HFSWR; amplitude comparison; beam forming

海洋公益性行业科研专项项目(201505002)；国家自然科学基金项目(41506114；61132005)资助

Supported by the National Marine Technology Program for Public Welfare(201505002)；National Natural Science Foundation of China (41506114；61132005)

2016-09-15;

2016-11-28

张玲(1978-)，女，副教授。E-mail:zljoan@163.com

TN971

A

1672-5174(2017)02-008-06

10.16441/j.cnki.hdxb.20160211

张玲，刘旭，姜義,等.一种阵列式高频地波雷达比幅测向新方法[J].中国海洋大学学报(自然科学版),2017,47(2):8-13.

ZHANG Ling,LIU Xu,JIANG Yi，et al.A novel amplitude comparison direction finding algorithm for array HFSWR[J].Periodical of Ocean University of China,2017,47(2):8-13.