基于等效电路的高频超方向天线互耦校正方法研究*

李春鹏，于长军，田潇潇

基于等效电路的高频超方向天线互耦校正方法研究*

李春鹏，于长军**，田潇潇

(哈尔滨工业大学(威海)信息与电气工程学院，山东 威海 264209)

岛基高频地波雷达由于受海岛特殊环境的影响，迫切需要减小接收天线阵尺寸。超方向圆型阵列拥有优良的方向特性，能够大幅度缩减天线阵面积，因此成为岛基高频地波雷达接收天线阵的一个重要发展方向。但是伴随着超方向阵列小型化的同时，天线阵元之间的物理间隔也必然随之变小，阵元之间的互耦效应会随着间距的变小而增强，而互耦则会使阵列性能急剧下降。近年来，对圆型阵列的互耦校正算法研究已经成为天线阵列校正领域的热点问题，本文以哈工大威海雷达站五元圆型接收天线阵为模型，采用等效电路法重点研究了互耦影响下超方向性天线的校正方法。通过计算机仿真验证了该方法的有效性。

高频地波雷达；互耦校正；超方向圆阵；阻抗匹配

天线阵构型中，将阵列方向性系数远大于相同阵元数的均匀阵列方向性系数的一类阵列统称为超方向性阵列[1],。超方向性天线(又称超增益天线)的一种通用的实用性定义为在对各阵元的均匀激励时，相同阵列结构，超方向性天线可以得到更高的方向性系数[2,3]。文献[4]指出，在小型化超方向性天线的设计研究过程中，随着阵元间距的减小，互耦对接收阵列性能的影响越来越大，传统的阵列综合及测向方法不能再被直接应用，需要对互耦进行补偿。

互耦校正的研究开始于1960年，Edelberg和Oliner[5]从无限阵列及边缘阵列两方面分析了互耦效应对大型天线阵的影响。实际应用中，天线阵元间的互耦的存在会对天线性能产生很大的影响，互耦的存在将使信号源相位向量产生畸变，从而影响协方差矩阵的特征结构，对角度估计会带

来很大的偏差。1989年，Yeh与Leou[6]提出抵消互耦产生的失真，得到近似的特征结构的方法，以实现对信号方位角的估计。Friedlander[7]于1991年通过对互耦矩阵的估计得到圆阵的互耦补偿方法。

互耦是天线之间固有的物理特性，是设计天线阵列，尤其是小型化的天线阵列时必须考虑的因素之一。互耦不但会影响天线阵的增益、波束宽度、旁瓣水平等参数，而且会影响阵列接收信号幅度与相位的一致性。由于布阵结构与电磁作用的复杂性，互耦的分析方法主要有等效电路法与矩量法[8]，其计算通常借助于电磁场的数值计算方法，本文采用等效电路法针对高频超方向天线进行互耦校正。

1 理论部分

1.1 等效电路法分析原理

等效电路法又称作开环电平法，因为它将无互耦时的天线阵看作为开环电路。对于一个M元的天线阵列，可以将其看作如图1所示的一个有M+1个端口的线性网络，图1中ZL为各阵元的等效负载，Vg为阵列激励电平，各端口的输出电平、电流分别为Vi、Ii，i=1,2,…,M+1。

令Zii为第i端口的自阻抗，Zij(i≠j)为第i端口与第j端口之间的互阻抗，其中i,j=1,2,…,M+1，则由基尔霍夫定理可得

V1=I1Z11+…+IjZ1j+…+IMZ1M+IM+1Z1(M+1)

⋮ ⋮ ⋮ ⋮ ⋮

Vj=I1Zj1+…+IjZjj+…+IMZjM+IM+1Zj(M+1)

⋮ ⋮ ⋮ ⋮ ⋮

VM=I1ZM1+…+IjZMj+…+IMZMM+IM+1ZM(M+1)。

(1)

图1 端口网络示意图Fig.1 Schematic diagram of port network

在不考虑端口之间的耦合现象时，可以把各端口看作开环电路，则Ii=0，又因Ii=Vi/ZL，代入可得Vi=Zi(M+1)IM+1，令这种情况下的Vi=Voi。使用该结论，考虑端口间的互阻抗，重新计算式(1)可得

(2)

写成矩阵形式为ZV=Vo，又可以写成V=Z-1Vo，表示将不存在互耦时的输出电平转换为考虑互耦时的输出电平，其中转换矩阵Z被称作为阵列的互阻抗矩阵，即互耦矩阵。

1.2 两种互阻抗定义

假设天线阵使用的是半波长偶极子天线，电流分布为正弦分布，并不考虑天线直径，如图2中所示。

图2 天线阵示意图Fig.2 Schematic diagram of antenna array

天线相关的教材资料中已经给出了传统自阻抗与互阻抗的求解公式[9]

Zii=Rii+jXii=30[Cin(2π)+jSi(2π)],

(3)

Z21=Z12=R21+jX21=R12+jX12,

(4)

(5)

(6)

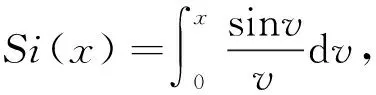
对式(5)与式(6)求解，就可以得到2个天线之间的互阻抗变化与物理间隔的关系。

假设如图2中所示的两个天线收到外部信源激励，并且在天线2上产生电流分布i(z)，i(z)作用到负载电阻上的电流值为I2。天线2上的电流分布i(z)重新辐射到自由空间并影响天线1，并在天线1的负载电阻上产生电平V1，那么接收天线的互阻抗可以定义为

(7)

1.3 互耦系数估计方法

假设互耦矩阵的第i行、第j列元素为ci,j，由式(2)和式(3)可以总结出M元均匀圆阵的互耦矩阵3个特点：

(1)c11=c22=…=cMM=1；

(2)当|i-j|=|m-n|时，i,j,m,n=1,2,…,M时，ci,j=cm,n；

(3)当i+m=M+2时，ci,1=cm,1。

由以上三点可以将M元均匀圆阵的互耦矩阵简化成

(8)

由式(8)可知，简化后的互耦矩阵参数数量减少，可以将其写成

(9)

其中：Eq(i,j)=δ(C(i,j)-cq)，当且仅当k=0时，δ(k)=1，其它情况时，δ(k)=0；P为自由度，即考虑的参数个数，因为互耦系数随着天线之间的物理间隔增加而变小，所以一般设定自由度等价于考虑的最大天线数目。自由度一般取阵元数的一半，以阵元数目M=5的圆型阵列为例，假设自由度P=2，则

(10)

(11)

(12)

由噪声子空间与真实信号空间正交的原理，可以求解线性约束方程，即

(13)

同样用Lagrange常数法求解，定义Lagrange函数

L(c,λ)=cHQ(θ)c-λ(wTc-1)。

(14)

令

(15)

由式(14)与式(15)得

(16)

将其写成矩阵形式为

(17)

对式(17)求解可得

(18)

将式(18)代回到式(13)可得

(19)

可以看到当wTQ-1(θ)w取得最大值时，就能使最小模约束成立，而且wTQ-1(θ)w与互耦矩阵无关。所以，可以利用wTQ-1(θ)w定义伪空间谱函数

(20)

其中Qz(θ)为Q(θ)第2行到第P行及第2列到第P列的子阵。

对式(20)所求得的伪空间谱搜索谱峰，就可以得到目标的回波方向，将其应用到式(18)就可以完成阵列互耦矩阵的估计，再使用估计出的互耦矩阵对阵列导向矢量修正，就可以使用传统空间谱算法对信号到达角进行估计了。

2 仿真分析

以威海雷达站高频地波雷达圆型接收阵为模型，如图3所示，通过HFSS仿真五元圆阵，分析阵元之间互阻抗的变化关系。

图3 威海雷达站高频地波雷达圆型接收阵Fig.3 Weihai radar HF radar circular receiving array

文献[10]给出了计算阵元之间的互阻抗随着半径的变化的方法。本文在HFSS软件中构造天线模型。具体仿真参数见表1。图4为阵列半径为1/2倍波长的互阻抗结果。

由于五元圆阵良好的对称性，Z12和Z15重合，Z13和Z14重合。上面结果可以证明互阻抗模值随着工作频率的提升而增加，也随阵列半径的缩小而增加，同时验证了(8)式。

图4 阵列半径为1/2倍波长

天线类型Antennatype天线长度/波长Lengthofantenna负载阻抗/ΩLoadimpedance天线直径/cmDiameter偶极子天线1/25010

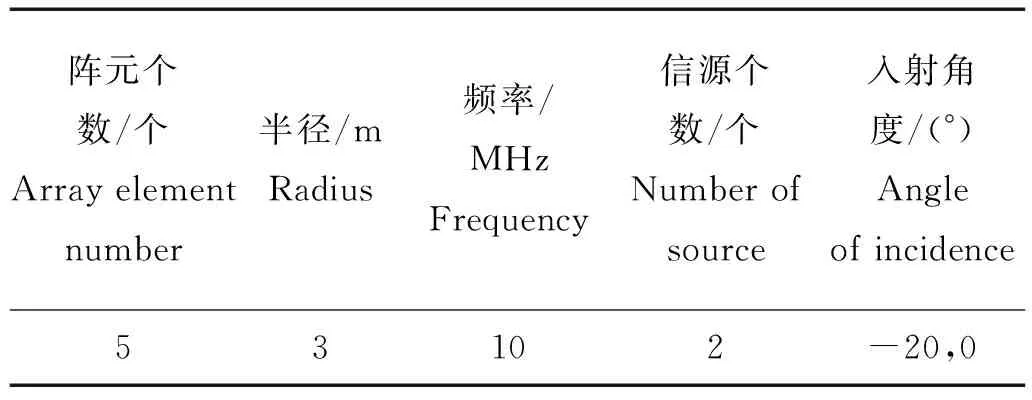
表2 超方向圆阵互耦校正仿真参数表Table 2 simulation parameters of the mutual coupling calibration of a circular array with a super orientation

以5元圆阵为模型仿真,参数见表2。等效电路法的步骤如下：

步骤2 构造对应不同θ(-90°～90°)的W矩阵，并由W矩阵求出Q(θ)；

从图5可以看到，伪空间谱剥离了互耦矩阵对到达角的影响，在一定程度上逼近了真实的到达角，而且通过图6的结果也证明了等效电路法的效果。

图5 伪空间普Fig.5 Pseudo space

图6 修正前后空间谱

文献[11]指出，圆阵互耦校正方法对参数估计时，均方根误差随着信噪比的增加而减小，并且可以高精度地对互耦误差参数的校正及对DOA的估计。图7为-20度信号源DOA估计的均方根误差仿真。信噪比由10～40 dB变化时，在每个信噪比下进行200次统计次数的蒙特卡罗实验，圆阵在10MHz对两个独立信号源互耦校正的结果。

图8为5元超方向圆阵，参数见表3。对其进行-10 dB效率约束下-25 dB的等旁瓣综合，得到互耦修正前后的方向图。其中,虚线代表互耦修正前方向图，由于互耦的影响旁瓣达不到-25 dB的要求，通过本文方法得到了较为理想的结果，如图中实线所示。

表3 超方向圆阵互耦校正参数表Table 3 Mutual coupling calibration parameter table for super directional circular array

图7 5元超方向圆阵互耦校正DOA估计性能

图8 互耦修正前后5元超方向圆阵方向图

3 结语

本文提出了一种使用等效电路对超方向圆形接收阵列进行互耦校正的方法。等效电路法对超方向阵列互耦校正具有较好的效果，尤其是在DOA估计精度和接收阵列的方向性方面有了较大的改善。等效电路法在使用时所需条件简单，易于编程，大大提高了接收阵列校正的适应范围，具有一定的实际应用价值。通过计算机仿真，验证了该方法的有效性以及可应用性。但是，文献[11]指出，超方向圆阵必须满足外部噪声占优的条件，这就限制了其半径和阵元个数的选取。因此，如何在满足超方向天线阵元个数、半径、效率基础上进行互耦校正，将是后续研究的重点。

[1] 华夏.小型化高频雷达接收阵列的研究[D].哈尔滨:哈尔滨工业大学,2011.HUA Xia.Research on Small Sized High Frequency Radar Receiving Array [D].Harbin:Harbin Institute of Technology,2011.

[2] 褚晓慧.岛基高频地波雷达天线研究[D].哈尔滨:哈尔滨工业大学,2015.CHU Xiaohui.Island Based HF Radar Antenna Research [D].Harbin:Harbin Institute of Technology,2015.

[3] Xiongbin W,Feng C,Zijie Y,et al.Broad Beam HFSWR Array Calibration Using Sea Echoes[C].Shanghai：2006 CIE International Conference on Radar,2006.

[4] 高火涛,李咏絮,郑霞.天线阵互耦系数的估计[J].通信学报,2005,26(4):19-23.GAO Huotao,LI Yongxu,ZHENG Xia,Estimation of mutual coupling coefficient of antenna array [J].Journal of communication,2005,26(4):19-23.

[5] Chao L,Xiongbin W,Bin L,et al.Array calibration for mutual coupling errors of high-frequency surface wave radar[J].IEICE Electronics Express,2012,9(8):731-738.

[6] Hui H T.Improved compensation for the mutual coupling effect in a dipole array for direction finding[J].Antennas and Propagation,IEEE Transactions on,2003,51(9):2498-2503.

[7] Chen K H,Kiang J F.Mutual coupling compensation in direction-of-arrival estimation with a linear dipole array[C].Memphis：Radio Science Meeting (Joint with AP-S Symposium),2014 USNC-URSI.IEEE,2014:116-116.

[8] 司伟建,吴迪,韩惠莲,等.均匀圆阵互耦自校正的级联估计方法[J].系统工程与电子技术,2014,36(7):1225-1231.SI Weijian,Wu Di,Han Huilian,et al.A cascade estimation method for mutual coupling of uniform circular array [J].System Engineering and Electronic Technology,2014,36 (7):1225-1231.

[9] 王朴中,石长生.天线原理 [M].北京:清华大学出版社,1993:102-103.Wang Puzhong,Shi Changsheng.Hntenna Theory [M].Beijing:Tsingghua University Press.1993:102-100.

[10] 于文启,陈建文,杨春山.一种天波超视距雷达电离层相位污染的校正算法[J].雷达科学与技术,2015,13(6):660-666.YU Wenqi,Chen Jianwen,Yang Chunshan.Correction algorithm of [J].radar science and technology for OTHR Ionospheric Phase contamination,2015,13(6):660-666.

[11] 邓维波,林力,袁楼.一种等间距圆形阵列的超方向性综合方法[J].哈尔滨工业大学学报,2001,33(6):838-841.DENG Weibo,Lin Li,Yuan Lou.A super directivity synthesis method for circular array with equal spacing [J].Journal of Harbin Institute of Technology,2001,33 (6):838-841.

责任编辑 陈呈超

Research on the Mutual Coupling Calibration Method for High Frequency Super Directional Antenna Based on Equivalent Circuit

LI Chun-Peng1,YU Chang-Jun2,TIAN Xiao-Xiao3

(School of Information and Electronic Engineering,Harbin Institute of Technology (Weihai),Weihai 264209,China)

Island based HF radar due to the influence of special island environment,the urgent need to reduce the antenna size.Super directional circular array direction has excellent characteristic,can greatly reduce the antenna area,so it has become an important direction of the island based HF radar array antenna.But along with the direction of ultra miniaturized array at the same time,the physical distance between array elements will become smaller,the mutual coupling between elements will be enhanced with the increasing of the distance is smaller,and the mutual coupling will make the array performance dramatically.In recent years,the mutual coupling of the circular array correction algorithm research has become a hot issue in the field of antenna array calibration,in order to hit five yuan round the Weihai radar antenna as a model school super directional antenna on the mutual coupling effect by using the equivalent circuit method is the key.The effectiveness of the proposed method is verified by computer simulation.

high frequency surface wave radar(HFSWR); mutual coupling correction; super-directive circular array; impedance matching

国家自然科学基金项目(61571159)资助

Supported by the National Natural Science Foundation of China(61571159)

2016-09-15；

2016-10-04

李春鹏(1991-)，男，硕士生。E-mail:lichunpeng1991@126.com

** 通讯作者：E-mail：yuchangjun@hit.edu.cn

TN957.51

A

1672-5174(2017)02-044-06

10.16441/j.cnki.hdxb.20160254

李春鹏，于长军，田潇潇.基于等效电路的高频超方向天线互耦校正方法研究[J].中国海洋大学学报(自然科学版),2017,47(2):44-49.

LI Chun-Peng,YU Chang-Jun,TIAN Xiao-Xiao.Research on the mutual coupling calibration method for high frequency super directional antenna based on equivalent circuit[J].Periodical of Ocean University of China,2017,47(2):44-49.