高频地波雷达海上目标航迹校正方法*

孙伟峰，周德明，戴永寿，周 鹏,李立刚，万 勇

(中国石油大学(华东)信息与控制工程学院，山东 青岛 266580)

高频地波雷达海上目标航迹校正方法*

孙伟峰，周德明，戴永寿，周 鹏,李立刚，万 勇

(中国石油大学(华东)信息与控制工程学院，山东 青岛 266580)

高频地波雷达对海上目标跟踪探测时，由于距离和方位角分辨率低且受到随机噪声的干扰，导致对目标位置探测不准确，形成的航迹会偏离目标的真实位置，影响跟踪的准确性。针对这个问题，结合海上特定目标跟踪的实际，本文从航迹的角度出发，基于对距离和方位角误差时间序列的统计建模，提出了一种基于同步船舶自动识别系统(Automatic Identification System,AIS)信息的高频地波雷达海上目标航迹校正方法。在高频地波雷达与AIS同步跟踪期间，采用统计回归的方法建立目标距离和方位角误差的校正模型；在高频地波雷达独立跟踪时，利用得到的模型分别对距离和方位角进行校正。利用实测高频地波雷达目标探测数据进行了航迹校正实验，校正后距离和方位角的均方根误差分别减少了约90%和75%，航迹跟踪效果得到了显著改善。

高频地波雷达； 目标跟踪； 航迹校正； AIS

高频地波雷达(High Frequency Surface Wave Radar,HFSWR)能够对海上运动目标进行超视距、大范围、全天候地主动跟踪探测，是海上目标监视监测的一种有效手段[1-3]。高频地波雷达探测目标时，受发射波形带宽和天线阵列孔径的限制，加之高频地波雷达自身系统误差及外界各种随机干扰的影响，距离和方位角的分辨率和精度都较低，导致探测得到的目标位置与目标真实位置之间存在较大偏离，跟踪得到的航迹偏离目标的真实运动轨迹，且存在剧烈波动，降低了目标跟踪的准确性。对于小阵列的紧凑型高频地波雷达，这个问题表现得更为突出。这给海上目标的准确跟踪带来很大的挑战，影响了高频地波雷达对海上运动目标进行独立跟踪探测时的性能，亟需发展有效的处理方法来提高目标跟踪的准确性。

围绕如何提高高频地波雷达目标探测时距离和方位角的分辨率和精度，国内外学者开展了系列研究工作。在提高目标测距精度方面，主要包括开展发射波形参数的设计，解决在无距离混叠、Doppler混叠的前提下，兼顾最大探测距离与距离分辨率[4]；以及利用旁瓣信息来提高距离分辨率[5]等。与距离测量相比，方位角测量的误差相对更大，是决定高频地波雷达对目标位置测量精度的关键因素。在提高目标方位角测量精度方面，主要包括在阵列导向矢量已知的理想阵列条件下，利用MUSIC(Multiple Signal Classification)、ESPRIT(Estimating Signal Parameters via Rotational Invariance Techniques)等超分辨率算法[6]，或是采用虚拟孔径技术[7]提高测角分辨率。然而，实际应用中阵列误差的存在会降低超分辨算法的性能。因此，也涌现出了很多阵列误差校准技术，比如，对单频信号正交解调误差的时域补偿法和频域补偿法，以及自适应通道校准方法[8]；基于自适应遗传算法的阵列无源校正方法[9]等。由于高频地波雷达系统自身及其周围环境的复杂性，阵列误差很难由这些校正方法完全消除。此外，也有研究者提出利用船舶自动识别系统(Automatic Identification System,AIS)的信息对高频地波雷达天线阵的幅相误差进行校正的方法[10-11]，这种方法无需布放校正源，由于AIS能够准确记录目标的位置信息，因而校正精度也很高。但是，这种方法的不足之处表现在：1)利用单个时刻的目标探测结果进行校正时，一是需要手动选取高信噪比的舰船回波信号，二是在信号处理阶段，仅依靠单个时刻的探测结果不易判定是否为真实目标；2)目标在不同时刻受到的干扰也不尽相同，此方法不能消除目标测量时各种随机干扰的影响。与此相比，综合多个时刻探测信息的航迹更好地反映了目标运动及高频地波雷达探测的特征，利用其对目标位置进行校正可以进一步提高目标探测的准确性。

基于上述考虑，本文从航迹的角度出发，提出了一种基于AIS信息的高频地波雷达海上目标航迹校正方法。该方法以同步跟踪期间特定目标的AIS航迹数据作为基准，分析与之匹配的高频地波雷达航迹数据中距离和方位角误差的变化规律并建立误差模型，在没有AIS数据时利用该模型实现对目标距离和方位角的校正。实测数据的航迹校正实验结果证明了方法的有效性。

1 高频地波雷达距离和方位角测量原理及误差分析

目标跟踪就是要准确地获取目标在不同时刻的空间位置，高频地波雷达在以雷达为极点的极坐标系下对海上目标进行探测，目标位置由距离和方位角共同决定。高频地波雷达对目标距离和方位角进行测量时，由于受高频地波雷达系统自身及外界干扰的影响，不可避免地会引入误差。本节将分别对高频地波雷达目标探测时距离和方位角的测量原理、误差来源及其影响因素进行分析。

1.1 距离测量原理及误差分析

(1)

其中：c为光速(c=3×108m/s)。因此，只要获得tr的值，便可计算出目标的距离；高频地波雷达一般采用调频中断连续波体制，tr会给信号带来一个整体的频偏Δf=αtr，α为扫频速率。对解线性调频后的信号做一次傅里叶变换即可得到Δf，进而获得目标的距离。

对式(1)作微分处理后，测距误差[12]可以表达为：

(2)

其中：Δc为电波传播速度平均值的误差；Δtr为测量目标回波延迟时间的误差。再考虑到噪声干扰的影响，高频地波雷达测距误差主要由电波传播速度变化产生的误差、测时误差以及混杂在回波信号中的噪声干扰(通常为带限加性高斯白噪声)引起的测量误差组成。其中，随着目标距离的增大，由电波传播速度的随机变化所引起的测距误差ΔR也会增大。

另外，从距离分辨率的角度来看，发射信号的有效带宽B决定了高频地波雷达的距离分辨率，有效带宽越宽，距离分辨率越高。根据线性调频高频地波雷达的原理，距离分辨率Δrc可以表示为

(3)

高频地波雷达工作在3～30MHz的高频段，频谱资源有限，且受到各种干扰的影响，限制了高频地波雷达发射信号的带宽，导致距离分辨率有限，一般为几公里到十几公里。高频地波雷达在进行目标探测时，其距离分辨率往往远大于目标尺寸而使得测距误差增大，形成的航迹偏离目标的真实运动轨迹。

此外，高频地波雷达对海上目标进行探测时，为了保证足够的多普勒分辨率，其相干积累时间一般较长(分钟量级)。在此相干积累时间内，目标可能会跨越几个距离单元格，造成距离模糊。上述这些因素都会给目标的距离测量带来误差。

1.2 方位角测量原理及误差分析

对海上目标探测时，目标方位角利用天线的方向性来测量。高频地波雷达天线将电磁能量汇聚在窄波束内，当天线波束轴对准目标时，回波信号最强，根据接收回波最强时的天线波束指向，就可以确定目标的方向。高频地波雷达一般采用阵列式天线，通过空间波束形成或方向扫描技术对目标方位进行估计。天线的方向性可以用其方向图来表示，方向图的一个主要技术指标是半功率波束宽度(half-powerbeamwidth,HPBW)，它表征了高频地波雷达的角度分辨能力，直接影响测角精度。

对高频地波雷达而言，波束主瓣宽度主要由天线阵元的数目及阵元间距确定。对于包含N个阵元，阵元间距为d0的线性阵列，其半功率波束宽度定义为[13]：

(4)

上式中：θ0为主波束的方向角；L为阵列长度。可见，当高频地波雷达的工作频率一定时，阵列长度越长，波束宽度越窄，方位角分辨率越高。然而，高频地波雷达的波长较长(10～100m)，若想获得较高的角度分辨率所需的阵列孔径较大，受海边天线阵地大小的限制，接收阵列的长度极为有限，一般采用小阵列天线，导致高频地波雷达的角度分辨性能较差。

另外，高频地波雷达一般布放在比较潮湿、盐碱度较高的海边，会逐渐导致天线阵元老化等问题，在目标测量时引入相位和幅度误差，影响目标方位角的估计精度。

由于关节电机的电流最大值为0.157 A，切割电机电流的最大值为1.5 A，负载反馈电流是H桥高侧电流的1/375，也就是说关节电机的负载反馈电流的最大值为0.157A/375，切割电机的负载反馈电流的最大值为1.5A/375，再经过200Ω的取样电阻进行I-V变换之后，关节电机的反馈信号最大为0.083 7 V，切割电机的反馈信号最大为0.8 V。经过74HC4052D的选通开关输出之后，反馈信号还需要经过信号放大才能接入ADC端口。

综上所述，由于受发射信号带宽和天线阵列孔径的限制，加之外部环境干扰的影响，高频地波雷达系统的距离分辨率和角度分辨率有限，测距、测角的精度都较低。尤其对于远端目标，由于方位角精度低所引起的切向距离误差将更大。然而，对于实际的目标测量数据而言，其位置误差是各种因素综合作用的结果，仅从距离和方位角测量误差形成原理的角度，很难得到一个理论上的校正模型。为此，本文采用数据驱动的思路，从目标跟踪得到的航迹数据中寻找距离和方位角误差的变化规律，进而建立校正模型。

2 基于AIS的高频地波雷达目标航迹校正方法

AIS与高频地波雷达是对海上目标进行监视监测的两种手段。AIS利用GPS或DGPS获取目标位置信息，GPS的精度为100m左右，而DGPS的实时定位精度可以达到3～5m以上，其目标定位精度比高频地波雷达高几个数量级，其不足之处在于探测距离较近，且属于被动探测手段。而高频地波雷达进行目标探测的优势在于超视距、全天候主动探测，其不足之处是目标定位精度差。为了更好地结合2种探测手段的优势，对关注的海上特定目标进行跟踪时，可以先将同步探测期间获取的特定目标的AIS信息作为基准，分析与之匹配的高频地波雷达航迹数据中距离和方位角误差的统计规律；当AIS数据缺失时，可以利用这一规律校正高频地波雷达航迹位置，提高高频地波雷达独立跟踪时对目标定位的准确性。基于这个思路，本文提出了基于AIS的高频地波雷达目标航迹校正方法，其流程如图1所示。

(1)数据同步与匹配

高频地波雷达与AIS在数据获取时间及获取位置信息形式方面存在差异，为了进行关联分析，首先需要实现两类数据的同步与匹配。利用坐标转换将AIS的经纬度位置表示转换为以高频地波雷达位置为极点的距离-方位角表示，然后对AIS时空数据进行线性插值[14]，得到与高频地波雷达数据获取时间对应的目标位置数据。

图1 航迹校正流程图Fig.1 Flowchart of track correction

(2)误差模型的建立

数据同步匹配后，对包含n个点迹的高频地波雷达与AIS航迹数据，将距离分量分别表示为Rri，Rai，方位角分量分别表示为θri，θai，i=1,2,…,n。分别计算两者间距离与方位角的差值，得到误差时间序列如下：

eri=Rri-Rai,i=1,2,…n，

eθi=θri-θai,i=1,2,…n。

(5)

高频地波雷达探测目标时的误差受诸多因素的共同影响，实测数据记录中的误差是各种因素的综合反映。一般来讲，高频地波雷达测量误差中包括了缓变的系统误差和快变的随机误差。高频地波雷达系统确定之后，这两部分误差都随着目标的RCS、运动参数和运动背景的变化而变化。因此，对于运动目标而言，高频地波雷达测量误差过程是一个具有均值趋势和时变方差的非平稳随机过程[15-16]。其中，表现为均值趋势的系统误差需要借助修正方法来消除，随机误差则可以通过平滑滤波来抑制。

考虑到高频地波雷达的测量误差与目标的运动参数有关，由于高频地波雷达测距精度相对较高，本文中主要考虑目标距离变化对测量误差的影响，将高频地波雷达测量误差建模为线性趋势项与随机误差项之和：

(6)

上式中：ar、aθ分别表示距离和方位角误差趋势项的斜率，br、bθ分别表示其截距；εri、εθ i分别表示距离和方位角误差的随机干扰项，一般将其建模为均值为零，方差时变的高斯随机过程。

对于距离误差数据，令

由式(5)给出的距离误差数据序列，利用最小二乘线性回归方法可以求取ar、br的值。同理，可以求取aθ、bθ的值，进而建立距离与方位角的校正模型。

值得注意的是，由于高频地波雷达测量数据受到各种随机干扰的影响，数据中会出现野值，且存在强烈波动，影响规律分析，需要去除野值并做平滑处理，以提高规律分析的准确性。本文采用3σ准则[17]剔除野值点的影响，采用高斯滤波对剔除野值点后的数据作平滑处理。利用处理后的数据进行误差模型参数的求解。(3)航迹校正

利用得到的距离和方位角误差模型，对k时刻得到的高频地波雷达目标点迹数据，其距离与方位角分别表示为Rrk、θrk，根据其测量距离分别推算出距离和方位角误差erk、eθk，进而得到该点位置的校正值：

(7)

以此类推，对航迹中的新增点迹，按照式(7)进行逐点校正，即可得到校正之后的航迹。

3 实验分析与讨论

本节采用实测高频地波雷达目标探测数据和同步的AIS数据对提出校正方法的有效性进行验证，并对校正结果进行分析评价。采用的高频地波雷达数据来自威海地波雷达站，于2011年10月31日录取。该高频地波雷达系统的工作频率为4.7MHz，采用8阵元的线性阵列作为接收天线，发射波形带宽为60kHz，理论计算的距离分辨率为2.5km；相干积累时间为60s。将AIS测量的目标位置数据作为真值，选取了两个典型的目标航迹个例进行分析，如图2所示。图2(a)中，目标的径向运动分量朝向高频地波雷达，图2(b)中，目标的径向运动分量远离高频地波雷达，两个目标的跟踪时长分别为35和60min。

由图2中的航迹对比结果可见，对于两个都沿直线行驶的目标，高频地波雷达探测得到的目标航迹与目标真实运动轨迹之间偏离较远，且存在波动。尤其对于个例2，探测航迹位置与目标真实位置之间存在较大差异。这是由于高频地波雷达对目标距离和方位角测量不准确导致的，下面将对目标距离和方位角的测量误差进行分析。

(1) 距离和方位角误差分析

对上述两个目标个例，按照式(5)分别计算距离和方位角误差序列，得到误差随距离的变化关系如图3所示。

由图3可见，对于两个目标，测距误差都小于2.5km，测角误差在7°以内。距离和方位角误差随距离的变化都

呈现出线性变化的趋势，且随着距离的增加，误差逐渐增大。可以采用线性回归的方式拟合出该趋势项，作为校正模型对测量误差进行趋势校正。

(2)拟合点数选取

假设待分析的航迹中包含n个目标点迹，为了对校正结果进行评价，选取前m个点迹数据进行误差建模，利用其余n-m个点迹数据对校正结果进行评价。m值不同，校正效果也不相同，下面，通过比较m取不同值时校正结果的均方根误差(RootMeanSquareError,RMSE)来对m的选取进行分析，如图4所示。

图2 高频地波雷达与AIS航迹比较(校正前)

由图4中的结果可以看出，随着参与回归分析的数据点数的增多，距离与方位角的均方根误差都是先呈现出递减趋势，后维持在一个稳定的水平。从误差变化曲线可以看出，目标位置测量误差主要由方位角误差决定，距离误差影响较小，这与高频地波雷达目标测量的实际情况是相符的。当采用25个左右的点迹数据(25分钟数据)进行模型参数计算时，均方根误差可以达到稳定的最小值。下面的实验中，都采用25个点迹数据计算误差模型参数。

(3)校正结果分析

受篇幅所限，仅对跟踪时间较长的个例2的校正过程及结果进行详细分析，对个例1仅给出最终的校正结果。对于个例2，由匹配的AIS和高频地波雷达航迹数据中的前25个点迹，分别计算得到距离和方位角误差序列，经野值点剔除及高斯平滑处理后，利用最小二乘法对误差序列随距离的变化规律进行线性回归分析，处理后的误差序列及回归结果如图5所示。

图3 距离和方位角误差随距离变化关系

实验中发现，对于不同的目标航迹，由于目标及其运动特点不同，得到的校正规律也不相同。利用回归分析得到的校正模型，对航迹中其余35个目标点迹分别进行距离和方位角校正，得到校正后的航迹结果如图6(a)所示，图6(b)给出了个例1航迹的校正结果。图6中，红色与黑色曲线分别表示校正前的高频地波雷达航迹与AIS航迹，绿色与蓝色的曲线共同组成校正后的高频地波雷达航迹，绿色部分表示模型训练数据，蓝色部分表示模型验证数据。由航迹校正结果可见，经过位置校正之后的航迹与目标真实运动轨迹之间的偏差明显减小。对于个例1，校正前后距离和方位角的均方根误差分别由2.12km、3.62° 减少至0.03km、0.52°；对于个例2，校正前后距离和方位角的均方根误差分别由2.25km、5.59°减少至0.08km、0.31°。

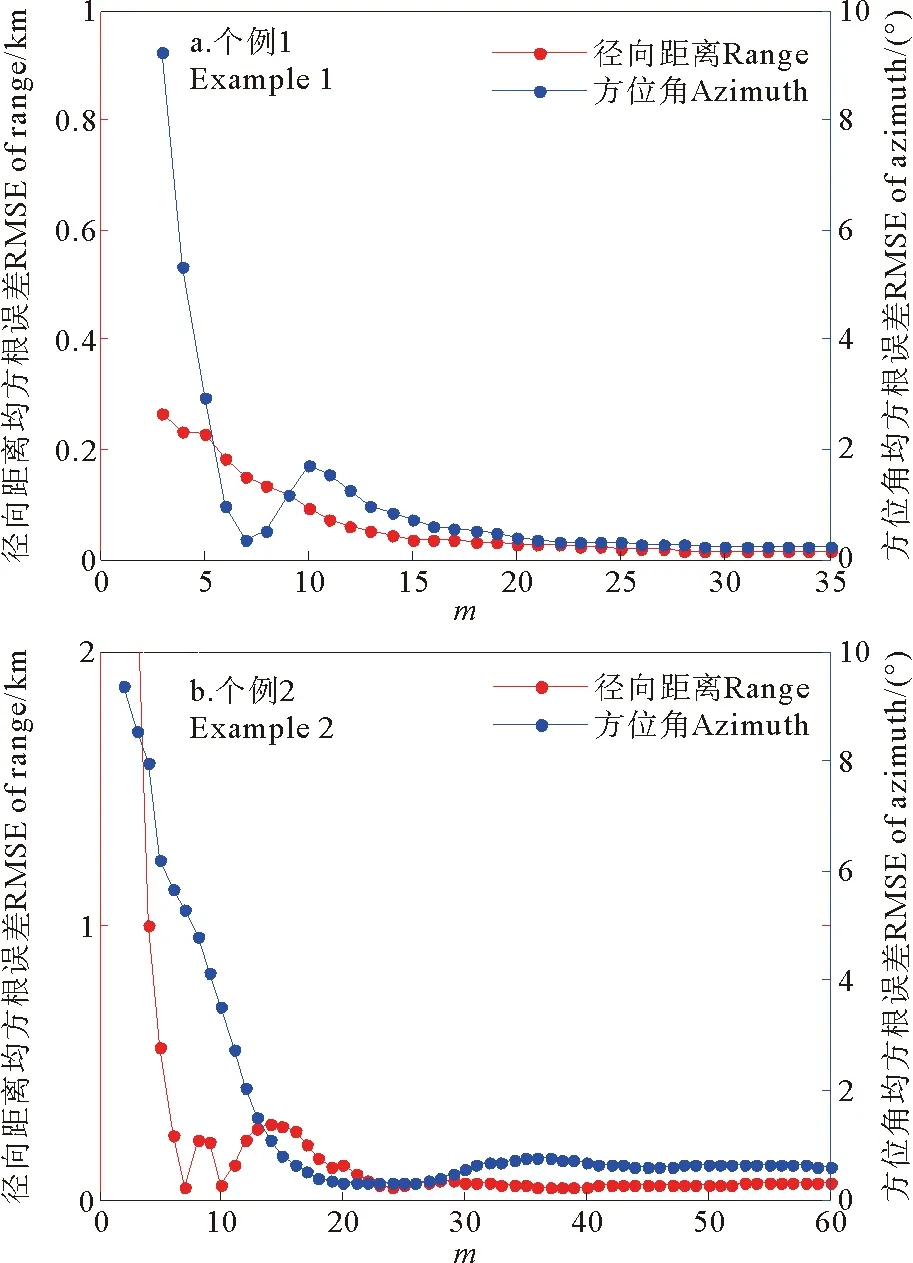
图4 不同m值下校正结果的均方根误差Fig.4 RMSEs underdifferent values of m

图5 误差回归结果Fig.5 Results of error regression

图6 校正前后航迹对比

采用相同的方法，对40条目标航迹进行校正实验，利用均方根误差准则对校正结果进行评价，得到校正前后目标距离和方位角的均方根误差曲线如图7所示。

图7 校正前后距离和方位角均方根误差对比Fig.7 RMSE comparisons before and after correction

由图7可见，采用本文提出的方法进行航迹校正后，距离与方位角的均方根误差都明显减小。校正前后距离均方根误差的平均值由2.42 km减小至0.24 km；方位角均方根误差的平均值由4.25°减小至1.04°，校正效果显著。

4 结论

结合高频地波雷达海上目标跟踪的实际，本文采用数据驱动的思想，从航迹信息的角度出发提出了一种基于AIS的高频地波雷达海上目标航迹校正方法，通过对目标距离和方位角测量误差的建模与校正，能够有效地提高对目标位置的探测精度。主要结论如下：

(1)基于航迹数据对距离和方位角测量误差随距离的变化进行线性回归建模，能够较好地反映误差的趋势变化，校正后距离和方位角的均方根误差分别可以减小90%和75%左右。

(2)对于不同的目标，其静态属性、运动参数及受到的外界干扰都不尽相同，采用数据驱动的方式建立的航迹校正模型更具有针对性。提出的方法利用25分钟的同步探测数据即可得到较好的校正结果，适用于对海上特定目标跟踪的应用场合。

如何利用更多的目标探测数据，建立整体的校正规律，对高频地波雷达探测范围内没有AIS数据的目标航迹进行趋势校正，是当前正在开展的研究工作。此外，校正后的航迹仍然存在波动，需要借助更好的跟踪滤波方法进行消除。

[1] A.M.Ponsford,J.Wang.A review of high frequency surface wave radar for detection and tracking of ships[J].Turk J ElecEng& Com Sci,2010,18(3):409-428.

[2] Vivone G,Braca P,Horstmann J.Knowledge-Based multi-target ship tracking for HF surface wave radar systems[J].IEEE Transactions on Geoscience & Remote Sensing,2015,53(7):3931-3949.

[3] Maresca S.,Braca P.,Horstmann J.,et al.Maritime surveillance using multiple high-frequency surface-wave radars[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(8):5056-5071.

[4] 杨子杰，柯亨玉，文必洋，等.高频地波雷达波形参数设计[J].武汉大学学报(理学版)，2001，47(5):528-531.Yang Z J,Ke H Y,Wen B Y,et al.Waveform parameters design for sea state detecting HF ground-wave radar[J].Journal of Wuhan University(Natural Science Edition),2001，47(5):528-531.

[5] 石阳升，文必洋，杨静，等.基于旁瓣信息的高频地波雷达高精度测距方法[J].中北大学学报(自然科学版)，2015，36(2):219-224.Shi Y S,Wen B Y,Yang J,et al.High precision ranging method for HF surface wave radar based on sidelobe information[J].Journal of North University China(Natural Science Edition),2015，36(2):219-224.

[6] 张翼，柯亨玉，程丰，等.基于MUSIC算法高频地波雷达的角分辨率[J].电波科学学报，2003，18(3):264-269.Zhang Y,Ke H Y,Cheng F,et al.Angle resolution of HF ground wave radar based on MUSIC scheme[J].Chinese Journal of Radio Science,2003，18(3):264-269.

[7] 莫期坚.高频地波雷达方位超分辨算法的研究[D].哈尔滨:：哈尔滨工业大学，2015.Mo Q J.Research on Azimuth Supper-Resolution Algorithm for HF Surface Wave Radar[D].Harbin :Harbin Institute of Technology,2015.

[8] 苏郢.高频地波雷达接收机的多通道幅相校准[D].武汉：武汉大学，2011.Su Y.The Amplitude and Phase Calibration Inmulti-Channel High-Frequency Receiverof Ground Wave Radar[D].Wuhan:Wuhan University,2011.

[9] 龙超，吴雄斌，柯亨玉，等.多频率高频地波雷达的阵列幅相校正[J].华中科技大学学报(自然科学版),2012，40(5):97-101.Long C,Wu X B,Ke H Y,et al.Array amplitude and phase calibration for multi-frequency HFSWR[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2012，40(5):97-101.

[10] 田文龙，李高鹏，许荣庆.利用自动识别系统信息进行高频地波雷达天线阵校正[J].电子与信息学报,2012,34(5):1065-1069.Tian W L,Li G P,Xu R Q.High frequency surface wave radar antenna array calibration using automatic identification system data[J].Journal of Electronics&InformationTechnology,2012,34(5):1065-1069.

[11] 唐庆乐.高频地波雷达舰船目标探测方位向估计与修正[D].青岛：中国石油大学(华东)，2013.Tang Q L.Ship Detection Direction Finding and Rectification for HFSWR[D].Qingdao:China University of Petroleum(East China),2013.

[12] 丁鹭飞，耿富录，陈建春.雷达原理[M].2版。北京：电子工业出版社，2009，265-271.Ding L F,Geng F L,Chen J C.Radar Principles[M].Bei Jing:Publishing House of Electronics Industry,2009.

[13] Ji Y,Zhan J,Wang Y,et al.Vessel target detection using zero-Doppler spectra of radar echo for high-frequency surface wave radar[J].IET Radar Sonar Navigation,2016,10(7):1243-1248.

[14] 周必全.雷达与AIS的数据融合及雷达性能评估[D].哈尔滨工业大学,2013.Zhou B Q.The Data Fusion of Radar and AIS and the Performance Evaluation of Radar[D].Harbin :Harbin Institute of Technology,2013.

[15] 杨文安，韩成标.基于白噪声的跟踪雷达量测误差建模与仿真[J].吉林大学学报(信息科学版)，2005,23(6):621-628.Yang W A,Han C B.Emulation and modeling based on measurement errors of white noises by tracking radars[J].Journal of Jilin University(InformafionScience Edition),2005,23(6):621-628.

[16] 齐全跃，陈敏.跟踪雷达测量误差的统计模型(I):模型的建立[J].应用数学学报，1997(1):1-10.Qi Q Y,Chen M.The statistical model of the tracking radar measuring error series(I)：Building model[J].ActaMathematicaeApplicataeSinca,1997(1):1-10.

[17] 卢元磊，何佳洲，安瑾，等.几种野值剔除准则在目标预测中的应用研究[J].指挥控制与仿真，2011，33(4):98-102.Lu Y L,He J Z,An J,et al.Research on rules for elimination outliers and its application to target prediction[J].Command Control & Simulation,2011，33(4):98-102.

责任编辑 陈呈超

A Maritime Target Track Correction Method for High Frequency Surface Wave Radar

SUN Wei-Feng,ZHOU De-Ming,DAI Yong-Shou,ZHOU Peng,LI Li-Gang,WAN Yong

(College of Information and Control Engineering,China University of Petroleum(East China),Qingdao 266580,China)

Low-power high frequency surface wave radars (HFSWR) have attracted great interests for their over-the-horizon coverage capability and continuous-time mode of operation.They are acting as effective long-range early warning tools in ocean remote sensing applications.When tracking maritime targets using HFSWR,low range and azimuth resolution and random noise interference will result in inaccuracy targeting.Thereafter the measured track will deviate from the target’s true trajectory with reduced tracking accuracy.According to the practical situations of specific maritime target tracking,a track correction method exploiting Automatic Identification System (AIS)iinformationis proposed for HFSWR from the aspect of track.The methodrelies on the statistical modeling of thetime seriesof range and azimuth errors with AIS data as groundtruth.Firstly,the outliers of the time series of range and azimuth errors are removed with a smoothing procedure followed.Thenrange and azimuth correction models are established by statistical regression methods during HFSWR and AIS synchronous tracking period.Finally,the measured range and azimuth are corrected via the established models to improve the tracking accuracy during independent tracking period of HFSWR.The results of track correction experiments using real HFSWR dataverify the effectiveness of the proposed method andthe range and azimuth errors can be reduced by about 90% and 75% on average respectively after correction,which indicate that the tracking performance can be significantly improved by the proposed method.

high frequency surface wave radar；target tracking；track correction；AIS

国家自然科学基金项目(61501520)；海洋公益性科研专项(201505002)；中央高校基本科研业务费专项资金项目(14CX02083A)；山东省自然科学基金项目(ZR2013FL035)资助

Supported by the National Natural Science Foundation of China(61501520)；Marine Scientific Research Special Funds for Public Welfare(201505002)；Fundamental Research Funds for the Central Universities(14CX02083A)；Shandong Provincial Natural Science Foundation(ZR2013FL035)

2016-09-15;

2016-11-25

孙伟峰(1982-)，男，副教授。E-mail:swf0217@163.com

TN958.93

A

1672-5174(2017)02-022-08

10.16441/j.cnki.hdxb.20160235

孙伟峰，周德明，戴永寿,等.高频地波雷达海上目标航迹校正方法[J].中国海洋大学学报(自然科学版),2017,47(2):22-29.

SUN Wei-Feng，ZHOU De-Ming，DAI Yong-Shou，et al.A maritime target track correction method for high frequency surface wave radar[J].Periodical of Ocean University of China，2017，47(2)：22-29.