Bulk-FFBP：基于距离向整体处理的快速分解后向投影算法

唐江文 邓云凯 王 宇 李 宁



Bulk-FFBP：基于距离向整体处理的快速分解后向投影算法

唐江文*①②邓云凯①王 宇①李 宁①

①(中国科学院电子学研究所 北京 100190)②(中国科学院大学 北京 100049)

距离向分块快速分解后向投影(Block-FFBP)算法通过子孔径合成降低了传统BP的算法复杂度，并且通过距离向分块，简化了繁琐的极坐标与直角坐标的转换。然而，距离分块操作使各块引入了斜距范围波动，而且插值核长度余量导致了算法的内存效率低下，从而降低了成像效率。该文提出一种基于距离向整体处理的Bulk-FFBP算法，并细分为基于距离向控制点的Bulk-FFBP以及无控制点的Bulk-FFBP。文中通过仿真对两种Bulk-FFBP算法进行了误差分析、成像性能分析以及算法效率分析，并与Block-FFBP算法进行对比，证实了Bulk-FFBP的优越性。

合成孔径雷达；后向投影算法；快速BP算法

1 引言

后向投影(Back-Projection, BP)算法是一种精确有效的合成孔径雷达(SAR)成像算法[1]，该算法在时域实现聚焦，因而能够很好地解决很多频域成像算法遇到的难题，比如距离徙动、SAR传感器的非直线飞行轨迹、方位空变等[2,3]。BP算法复杂度为(3)，高于一般频域成像算法的复杂度(2lg)，这成为限制其广泛使用的巨大障碍。在使用BP算法进行成像时，一般都需要性能强劲的计算平 台，然而，借助于计算平台并不能改变BP算法(3)计算复杂度的事实。

快速BP算法对BP算法结构进行了改进，利用了子孔径角频率带宽有限的性质[7]，将全孔径积分分割成子孔径积分的组合，以降低计算复杂度。其中文献[8]采用了两级算法结构实现了计算复杂度为(2.5)的快速BP算法，文献[9]采用多级算法结构实现了计算复杂度为(2lg)的快速BP算法。文献[10]提出了快速分解BP算法(Fast Factorized Back-Projection, FFBP)，并对斜距误差进行了分析，另外还提出了在距离向分块的FFBP算法(Block-FFBP)，简化了极坐标与直角坐标之间繁琐的转化计算。文献[11]提出了一种结合波数域频谱拼接的快速BP算法，但仍在极坐标系下进行，并且子孔径成像之后采用了类似极坐标格式算法(PFA)的频域处理，一定程度上丧失了BP不受波前弯曲影响的特点[1]。文献[12,13]对FFBP算法进行了改进，但成像操作仍然是在极坐标系下进行的。

文献[10]中指出，Block-FFBP算法缺陷在于增加了算法需要的内存空间，这是因为分解过程中每一块对应的斜距范围不同，需要的存储空间存在波动；另一方面Block-FFBP使用插值核进行插值，需要一定余量以保证边缘点的插值效果。文献[14]给出了一种优化的分块策略，但并没有完全消除分块带来的问题。本文对Block-FFBP算法进行改进和优化，提出了一种对相同方位向的波束进行整体处理的Bulk-FFBP算法，降低了额外的内存消耗，提升了算法的计算效率，且更加易于实现。

接下来的内容安排如下，第2节对Block-FFBP进行介绍，并指出Block-FFBP存在的缺陷；第3节对Bulk-FFBP算法进行详细的描述和分析；第4节对Bulk-FFBP算法进行仿真验证；最后对本文进行了总结。

2 Block-FFBP算法

2.1 Block-FFBP算法基本步骤

Block-FFBP算法是在FFBP算法的基础上，对距离向进行分块处理。以基数为2的8孔径Block-FFBP为例(如图1)，在SAR飞行轨迹上有8个孔径，每个孔径对应一个指向成像场景的波束，第1步如图1(a)，将相邻两个孔径进行子孔径合成，同时在距离向上进行分块，这样就得到了右侧方位向和距离向2×2的4个波束，而孔径减少了一半，变为4孔径；第2步分解为图1(b)右侧的2孔径，16波束；同理第3步得到图1(c)右侧的1孔径，64波束。当然，分解的层数以及选用的基数可自由选择，最后通过一步传统BP算法实现最终成像。由于经过多级分解，场景尺寸小了，孔径数也少了，最终的BP成像计算量也就大大降低了。

图1 基数为2的8孔径Block-FFBP各级子孔径合成示意图

2.2 Block-FFBP存在的问题

普通的FFBP算法，是通过繁复的极坐标和直角坐标转换来确定成像点与新旧孔径之间斜距的关系，而Block-FFBP的波束指向中心点是在直角坐标系中直接选定的，计算出中心点到孔径斜距，也就确定了当前块到孔径的中心斜距，块内其他点的斜距为中心斜距加减一个斜距范围，从而简化了计算。

Block-FFBP也存在一些问题，一方面，新孔径在合成过程中需要进行插值操作，由于距离向分块，数据不断被截断，无法通过统一的FFT进行插值，只能通过插值核进行，而插值核是有一定长度的，为了保证斜距边缘点的插值效果，波束数据长度需要有一定的插值余量，随着分解级数增多，插值余量所占的空间比例越来越大，导致内存空间需求不断增长(如图2)。另一方面，即使不考虑插值余量所占空间，有效数据由前一级孔径合成到新一级孔径时，所需要的内存空间也并不完全一致，会产生波动。

总之，从算法实现的角度来看，Block-FFBP需要更多的内存空间，并且内存空间的动态增长会降低算法的计算效率。

3 Bulk-FFBP算法

3.1 基于距离向控制点的Bulk-FFBP

Block-FFBP的缺陷在于，分块操作导致内存需求会增长。这里给出一种Bulk-FFBP算法，主要思想是不在距离向上进行分块，而是选取一些固定的控制点，来确立成像点到新旧孔径斜距之间的关系。

图2 Block-FFBP插值核余量需求空间不断增长

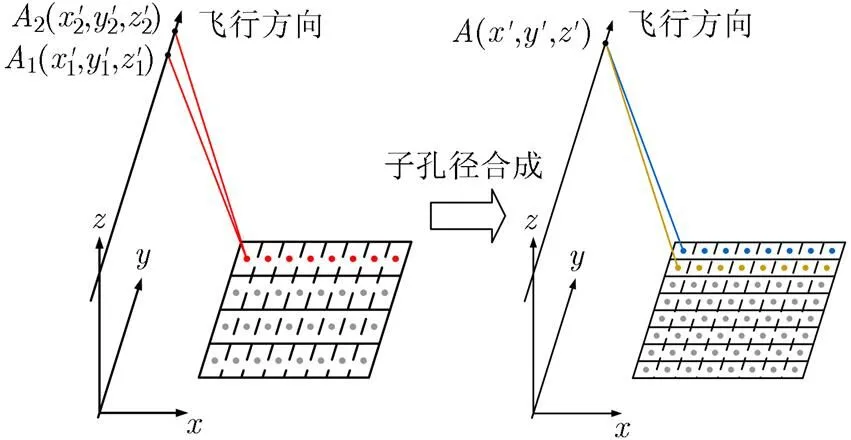
图3 Bulk-FFBP对于方位向相同的波束在距离向选择数量固定的控制点

图4给出了局部放大图，B(x,,)是成像平面内的一个波束控制点，设斜距1B的长度为1i，斜距2B的长度为2i，孔径合成后AB的长度为l，则B到3个孔径的回波延迟分别为

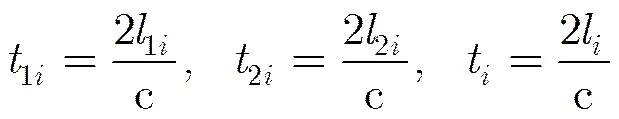
其中，c为光速。设孔径1的距离压缩回波为1()，孔径2的距离压缩回波为2()，孔径的距离压缩回波为()，那么子孔径合成的过程可表示为

(2)

其中，0为SAR信号的载频。对于一对对应的延迟时间{t,t}，可以设计一组插值函数，表征合成后孔径的回波延迟到合成前各孔径A回波延迟的映射关系，即

把插值函数代入式(2)就可以得到

(4)

式(4)就是孔径1,2到的子孔径合成公式，可以看出通过插值得到了子孔径合成的连续表达式，不再存在Block-FFBP中数据截断的问题，相同方位向的波束回波成为一个整体，所以称为Bulk- FFBP，如此一来，对回波数据的插值就可以通过整体的FFT升采样来进行，提高了插值效率。

3.2 无控制点的Bulk-FFBP

在前面的基础上，我们对l和l(=1,2)的展开形式进行分析，有

(6)

将式(1)代入式(6)可得

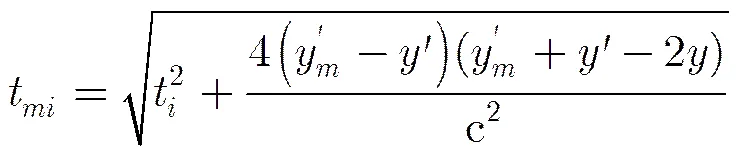
如果将离散的{t,t}替换为连续的{t,}，则有

(8)

这样就直接得到了当前孔径回波延迟和下一级孔径回波延迟之间的关系，式(4)也就可以写为

这样就把回波延迟的表示方式由基于控制点的插值转换为具体的解析表达式，减少了计算量。如果没有水平直线飞行的前提条件，那么也可以从式(5)推出更严格的形式，形式较繁复，在此不再展开。以上展示的是基数为2的孔径合成，其实也可以扩展到其他整数基数上。同样，无控制点Bulk- FFBP也可以使用FFT升采样进行高效的插值计算。图5给出了两种Bulk-FFBP的算法流程图，可以看出两种算法的区别是，控制点Bulk-FFBP的斜距来自基于控制点的拟合，而无控制点Bulk-FFBP的斜距来自直接计算。

图5 两种Bulk-FFBP的算法流程图

3.3 误差分析

接下来，我们对Bulk-FFBP的斜距误差以及Block-FFBP的斜距误差进行对比。Block-FFBP的斜距误差来源于，成像点到新旧孔径的回波延迟并不一致，对于Block-FFBP来说只有场景块中心点到新旧回波延迟可以保证一致，其他成像点都存在误差。图6示意了Block-FFBP某块场景，图中当前孔径为，上一级某孔径为A，场景块中心点为，块中任意点，斜距,,AB,AC的长度分别表示为l,l,l,l,点由于位于场景中心，不存在斜距误差，而对于点，它相对上一级孔径A的斜距为l，而通过当前孔径映射到上一级孔径A的斜距为，因此点的斜距误差为

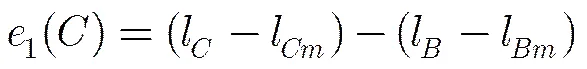
设l,l,l,l对应的回波延迟时间为t,t,t,t，那么式(10)表示成传播延迟误差则为

(11)

对于Bulk-FFBP，假设使用式(4)控制点的方法，为距离向控制点之一，结合式(3)，点的回波延迟误差可以表示为

同样，如果使用式(9)无控制点方法，结合式(8)，式(9)，点的回波延迟误差为

(13)

下面通过数值的方法对block(),bulk1()和bulk2()进行分析对比。参照图6，设置情景为水平直线飞行的机载SAR，高度为8000 m，下视角为, C波段，载频为5.4 GHz，设置不同的斜视角分别为，孔径和A之间的间隔|AA|分别为1 m, 10 m, 100 m, 1000 m，选取的矩形场景大小以1()引起的相位误差不超过为准，即，然后绘制出场景内500×500点中相位误差1(),2()和3()各自的最大值，结果如图7所示，图中相对进行了归一化，其中控制点Bulk-FFBP算法中的使用的是3次样条插值。图中被虚线分隔开的区域对应不同的斜视角，同一区域内不同的点对应不同的孔径间隔，孔径间隔顺序为1 m, 10 m, 100 m, 1000 m，可以看出在孔径间隔小斜视角度小的情况下，Bulk-FFBP与Block-FFBP相差不大，而当孔径间隔增大或者斜视角度增大时，Bulk-FFBP的相位误差就逐渐小于Block-FFBP，因此从误差分析的角度来看，Bulk- FFBP是优于Block-FFBP的。

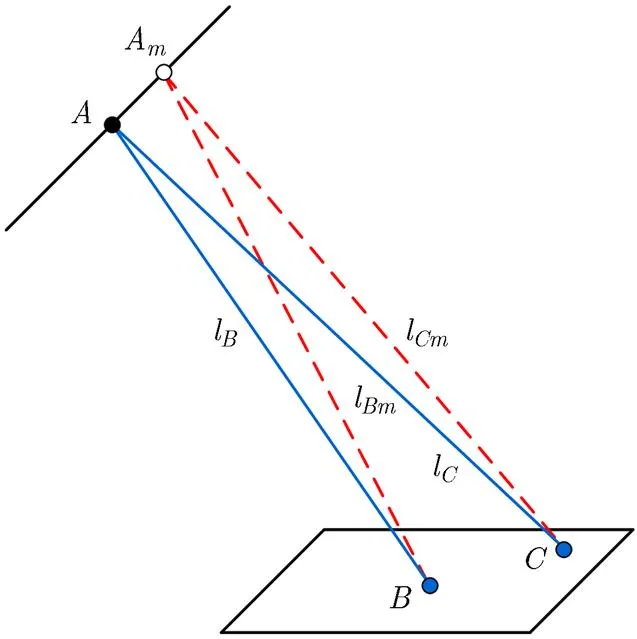
图6 Block-FFBP与Bulk-FFBP误差分析模型

图7 两种Bulk-FFBP与Block-FFBP相位误差对比

4 仿真实验

4.1 点目标性能对比

为了对Bulk-FFBP和Block-FFBP有更加直观的印象，这里设计了一组X波段星载聚束SAR仿真参数进行点目标性能对比，具体参数如表1所示。

表1 X波段星载聚束SAR仿真参数

场景中心设置了点目标，仿真得到的回波尺寸为方位向20000点，距离向24000点，然后分别使用Block-FFBP、控制点Bulk-FFBP、无控制点Bulk-FFBP对回波进行基数分别为4, 4, 5, 5的4级分解成像处理，其中控制点Bulk-FFBP在距离向均匀等距设置30个控制点，采用3次样条插值。成像大小为12000×12000，场景尺寸为2 km× 2 km。

3种算法的点目标成像结果及距离向和方位向剖面如图8所示，表2给出了该点目标的具体性能指标，从表中可以看出，在距离向上，两种Bulk- FFBP算法的峰值旁瓣比PSLR优于Block-FFBP约2.2 dB，积分旁瓣比ISLR优于Block-FFBP约3.7 dB，这是因为Block-FFBP算法由于数据截断无法使用FFT进行插值，而使用了8点sinc插值，在逐级的sinc插值过程中，振铃现象被放大[15]，而两种Bulk-FFBP采用的是FFT升采样插值；在方位向上，两种Bulk-FFBP略优于Block-FFBP约0.1 dB。

4.2 算法效率对比

接下来对Block-FFBP以及两种Bulk-FFBP算法的运算效率进行对比，3种算法都使用单线程运行。为了便于分析，我们对距离压缩后的数据进行了裁剪，以缩短成像时间，裁剪后方位向为2048个点，距离向为1024点，之后进行基数为4的分解成像处理，成像大小为1024×1024。

表3给出了3种算法的运行时间及相对传统BP的加速比(倍)，可以看出3种算法的速度相对于传统BP都有提升，而且随分解级数的增多，加速比也在增加，两种Bulk-FFBP算法整体上比Block- FFBP的速度更快，这是因为Block-FFBP距离向分块内存效率低下，并影响了计算效率。尤其是，在5级分解时，Block-FFBP的加速比相对于4级分解反而降低了，这是因为插值余量所占的空间超过了有效数据本身的空间，导致计算效率严重下降。

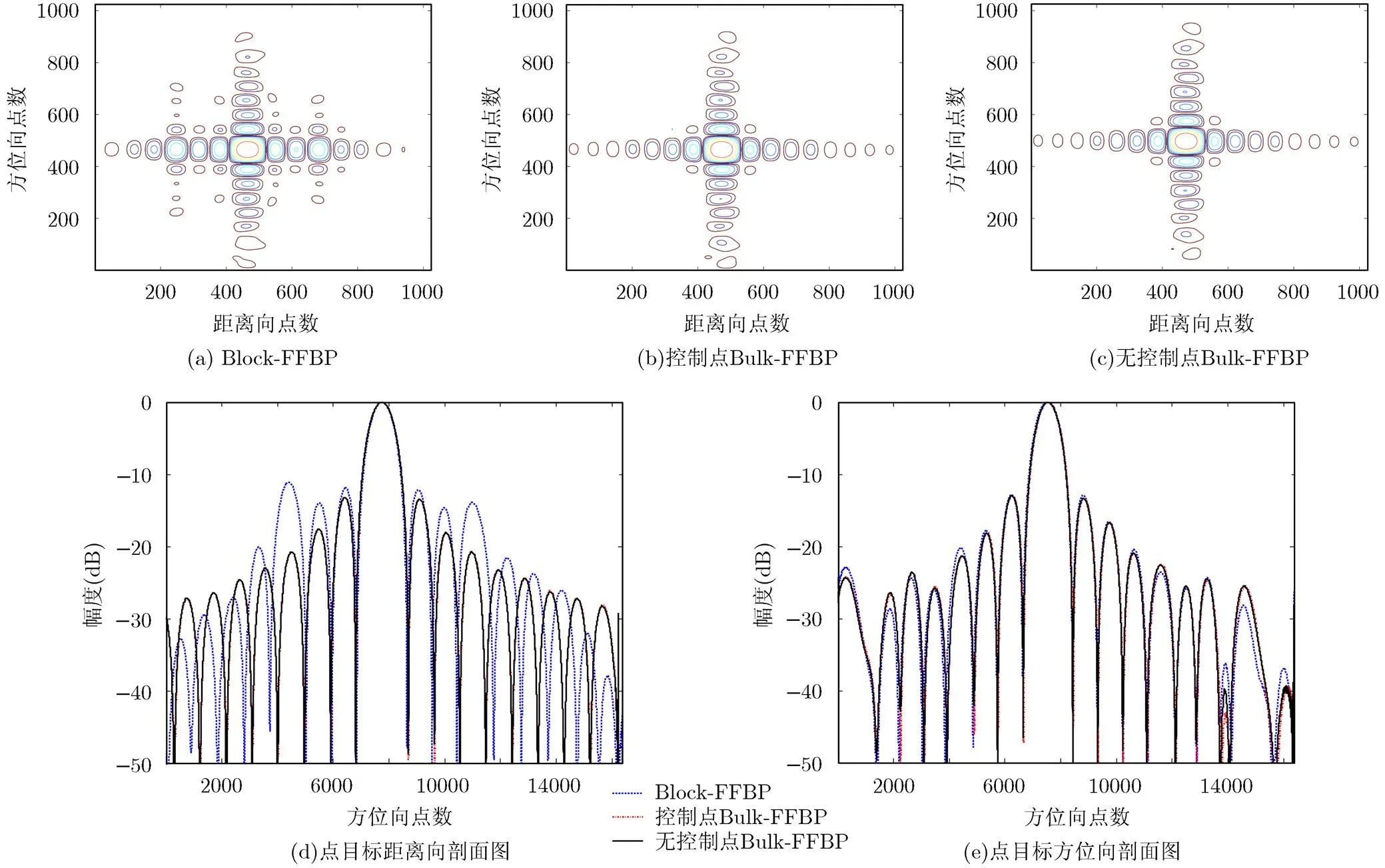
图8 Block-FFBP与两种Bulk-FFBP点目标成像对比

表2 点目标性能对比

表3 不同分解级数成像用时(s)及加速比(倍)

5 总结

本文针对Block-FFBP算法由于距离向分块造成的数据截断及效率瓶颈问题，提出了基于距离向整体处理的Bulk-FFBP算法，在算法的推导过程，又将Bulk-FFBP算法细分为两种，一种是基于距离向控制点的Bulk-FFBP算法，另一种是无控制点的Bulk-FFBP算法。文中通过误差分析、成像性能分析以及算法效率分析，证实了这两种Bulk-FFBP算法相对于Block-FFBP算法的优越性。

[1] DESAI M D and JENKINS W K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar[J]., 1992, 1(4): 505-517. doi: 10.1109/83.199920.

[2] SOUMEKH M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms[M]. New York, Wiley, 1999: 212-215.

[3] MENG D, HU D, and DING C. Precise focusing of airborne SAR data with wide apertures large trajectory deviations: a chirp modulated back-projection approach[J]., 2015, 53(5): 2510-2519. doi: 10.1109/TGRS.2014.2361134.

[4] CAPOZZOLI A, CURCIO C, and LISENO A. Fast GPU- based interpolation for SAR backprojection[J]., 2013, 133: 259-283.

[5] FREY O, WERNER C L, and WEGMULLER U. GPU- based parallelized time-domain back-projection processing for Agile SAR platforms[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Quebec City, Canada, 2014: 1132-1135.

[6] PRITSKER D. Efficient global back-projection on an FPGA[C]. IEEE Radar Conference. Arlington, VA, USA, 2015: 0204-0209.

[7] BASU S and BRESLER Y.(2log2) filtered backprojection reconstruction algorithm for tomography[J]., 2000, 9(10): 1760-1773. doi: 10.1109/83.869187.

[8] YEGULALP A F. Fast backprojection algorithm for synthetic aperture radar[C]. Proceedings of 1999 IEEE Radar Conference, Waltham, MA, USA, 1999: 60-65.

[9] XIAO S, MUNSON J D C, BASU S,. An2logback-projection algorithm for SAR image formation[C]. Thirty-Fourth IEEE Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 2000, 1: 3-7.

[10] ULANDER L M H, HELLSTEN H, and STENSTROM G. Synthetic-aperture radar processing using fast factorized back-projection[J]., 2003, 39(3): 760-776. doi: 10.1109/TAES. 2003.1238734.

[11] ZHANG L, LI H, QIAO Z,. A fast BP algorithm with wavenumber spectrum fusion for high-resolution spotlight SAR imaging[J]., 2014, 11(9): 1460-1464. doi: 10.1109/LGRS.2013. 2295326.

[12] 左绍山, 杨泽民, 孙光才, 等. 基于几何校正的聚束SAR快速分级后向投影算法[J]. 电子与信息学报, 2015, 37(6): 1389-1394. doi: 10.11999/JEIT141254.

ZUO Shaoshan, YANG Zemin, SUN Guangcai,. Geometric correction based fast factorized back projection algorithm for spotlight SAR imaging[J].&, 2015, 37(6): 1389-1394. doi: 10.11999/JEIT141254.

[13] 杨泽民, 孙光才, 吴玉峰, 等. 一种新的基于极坐标格式的快速后向投影算法[J]. 电子与信息学报, 2014, 36(3): 537-544. doi: 10.3724/SP.J.1146.2013.000613.

YANG Zemin, SUN Guangcai, WU Yufeng,. A new fast back projection algorithm based on polar format algorithm[J].&, 2014, 36(3): 537-544. doi: 10.3724/SP.J.1146.2013.000613.

[14] JIANG X, WANG J, QIAN S,. SAR imaging using fast factorized backprojection based on optimal regional partition [C]. IEEE Radar Conference. Cincinnati, OH, USA, 2014: 0229-0232.

[15] CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. London, Artech House, 2005: 52-59.

Bulk-FFBP: Fast Factorized Back-projection Algorithm Based on Range Bulk Processing

TANG Jiangwen①②DENG Yunkai①WANG Robert①LI Ning①

①(,,100190,)②(,100049,)

Block Fast Factorized Back-Projection (Block-FFBP) algorithm adopts a subaperture synthesis approach to reduce the computing complexity of the conventional BP algorithm, and partitions the echo data into blocks in range to avoid the complicated transforms between polar and Cartesian coordinates. However, Block- FFBP results in a range span vibration of the data blocks, and Block-FFBP needs an extra data length associated with the interpolation kernel. That gives rise to the inefficiency of the memory, and furthermore the degradation of the imaging speed. A range Bulk processing based FFBP (Bulk-FFBP) algorithm is proposed in this paper. It is implemented in two ways. One is based on a series of range pivots, and the other one is of no pivots. The outperformance of Bulk-FFBP relative to Block-FFBP is verified through simulations in error analysis, imaging evaluation and computing efficiency test.

Synthetic Aperture Radar (SAR); Back-Projection (BP) algorithm; Fast BP algorithm

TN957.52

A

1009-5896(2017)02-0405-07

10.11999/JEIT160373

2016-04-18；改回日期：2016-06-20；

2016-09-08

唐江文 jiangwen@mail.ustc.edu.cn

中国科学院“百人计划”(61422113)，国家“万人计划”

The “Hundred Talents Program” of the Chinese Academy of Sciences (61422113), The National Ten Thousand Talent Program-Young Top-Notch Talent Program

唐江文： 男，1988年生，博士生，研究方向为SAR时域成像算法及大规模并行计算.

邓云凯： 男，1962年生，研究员，博士生导师，研究方向为星载SAR系统设计、成像及微波遥感理论.

王 宇： 男，1980年生，研究员，博士生导师，研究方向为星载SAR系统设计及信号处理.