基于CFD的轮胎滑水及其性能影响因素分析
周海超,陈 磊,翟辉辉,雷利利
(1.江苏大学 汽车与交通工程学院,江苏 镇江 212013;2.镇江高等专科学校 汽车工程学院,江苏 镇江 212013)
基于CFD的轮胎滑水及其性能影响因素分析
周海超1,陈 磊1,翟辉辉2,雷利利1
(1.江苏大学 汽车与交通工程学院,江苏 镇江 212013;2.镇江高等专科学校 汽车工程学院,江苏 镇江 212013)
轮胎滑水性能对车辆安全性和操控性具有决定性影响,而花纹结构设计参数直接影响着轮胎接地区水流运动进而对轮胎滑水性能也会产生直接影响。但由于滚动轮胎的滑水性能测试条件极为苛刻,且很难捕获到滑水现象发生时水流运动流场特性。为明晰滑水现象发生时的流场特性及花纹结构设计参数对滑水性能的影响,基于计算流体动力学的方法,建立考虑轮胎接地印痕及花纹变形特征的滑水分析模型,掌握了水膜升力、自由液面及沟槽内水流速度等流场分布特征,分析了水膜厚度、水流速度、纵向花纹及横花纹结构设计对滑水性能的影响。结果表明:在水膜厚度较小时,路面水流可顺畅进入接地区花纹沟并被及时排出;水流速度的变化对胎面动水压力有显著影响;纵向花纹沟深度对滑水性能影响显著;改变横向花纹沟水流运动方向、降低胎面动水压力可提升滑水性能。
车辆工程;轮胎滑水;花纹设计;流场特性;仿真分析
0 引 言
汽车在有水膜路面行驶时,轮胎与路面接触区花纹沟内会存有一定量的积水,随着行驶速度的提高,当花纹沟不能完全排除或无法排除积水时,在轮胎与路面间会产生动水压力,使轮胎与路面逐渐脱离接触,直至发生“滑水”,此时轮胎的附着性能显著降低,严重影响行车安全。因此,轮胎与路面间会产生动水压力,使轮胎与路面逐渐脱离接触,直至发生“滑水”,此时轮胎的附着性能显著降低,严重影响行车安全。因此,研究轮胎发生滑水时花纹沟内的水流运动特征以及花纹结构设计对提升轮胎抗滑水性能显得尤为必要。
由于受滑水测试条件的限制,数值计算方法如数学物理模型[1]、有限体积法(FVM)[2]、任意拉格朗日欧拉法(ALE)[3]等成为认识轮胎滑水现象的主要途径。其中,ALE方法可兼顾轮胎在滚动过程中的花纹变形及流固耦合作用,在一定程度上可真实反映轮胎花纹与水流间的相互作用,成为轮胎滑水性能研究的主要方法。但由于该方法在模型中引入了拉格朗日单元,不能有效处理网格扭曲情况,从而造成计算周期延长[4]。此外,ALE方法重点关注轮胎产生动水压力的过程,不能灵活地对花纹沟内流场微观特性进行研究。计算流体动力学(computational fluid dynamics,简称CFD)采用离散的代数形式求解N-S方程,可得到流场参数在离散点处的数值[5],同时CFD方法能有效捕捉流体自由液面和重现流场微观特性,可视为轮胎滑水现象发生时流场特性,且计算效率高[6]。
花纹结构是影响轮胎滑水性能的主要因素。B.WISE等[7]通过试验测试了不同花纹结构对轮胎临界滑水速度的影响。S.K.SANTOSH等[8]的研究表明,对于纵向花纹,花纹沟深度和宽度每增加1 mm,车辆滑水速度则分别增加1.6 km/h和6.8 km/h;对于横向花纹相应增加1.6 km/h和5.5 km/h。王长建等[9]指出混合花纹型式能显著提高轮胎临界滑水速度。但上述研究主要针对花纹沟宽度和深度对轮胎滑水性能的影响,忽视了花纹间距及横沟结构型式对轮胎滑水性能的影响,且对轮胎滑水现象产生时的水流流场特征研究鲜有报道。
笔者将采用计算流体动力学的方法,借助ABAQUS在获得滚动轮胎接地特征后,采用逆向重构技术建立了考虑花纹沟接地变形特征的轮胎滑水分析模型。从微观流场角度分析了轮胎滑水过程中的水流特征及胎面动水压力分布等流场特性。研究了轮胎在不同水膜厚度、不同水流速度及不同纵向、横向花纹结构设计对轮胎滑水性能的影响,为高性能轮胎花纹结构设计提供了依据。
1 轮胎滑水模型的建立
1.1 滑水物理模型
以205/50R16乘用车子午线轮胎为研究对象,施加载荷4 000 N,气压240 kPa。其中,胎面纵向花纹沟深8 mm,宽9 mm。轮胎橡胶材料采用Yeoh模型,利用ABAQUS建立带花纹轮胎的有限元模型,借助任意拉格朗日欧拉方法获得某一稳定速度下轮胎接地印迹及花纹沟变形特征,如图1。

图1 滚动轮胎接地印迹及花纹沟变形特征(90 km/h)Fig.1 Rolling tires contact patch and deformation characteristics of pattern groove(90 km/h)
以负载轮胎变形后的花纹网格单元为信息,采用由离散单元到实体模型的逆向建模方法,建立轮胎滑水模型。文献[10]确定轮胎滑水计算域的长为1 500 mm,宽为370 mm,高为40 mm,滑水计算域及边界条件设置如图2;考虑到胎面花纹的对称性,取其1/2进行分析;采用多块网格技术进行网格划分,将计算域离散为五面体结构化网格与四面体非结构化网格的混合网格,对流体运动变化剧烈的轮胎接地前端和花纹沟内单元进行细化,最终模型单元总数为1 358 587,节点总数为1 272 427。

图2 轮胎滑水模型及边界条件设置Fig.2 Tire hydroplaning model and the set of boundary conditions
1.2 数学模型
1.2.1 控制方程
轮胎滑水性能控制方程采用不可压缩流体的连续性方程(1)与RANS方程(2):
(1)
(2)

1.2.2 湍流模型
采用Yakhot及Orzag提出的RNGκ-ω湍流模型[11],该模型利用重整化群理论对κ-ω湍流模型进行修正,可较好地处理高应变率及流线弯曲程度较大的流动。对于近壁区湍流发展不充分的问题,采用增强壁面函数法近似处理。
1.2.3 自由液面的捕捉
对于自由液面绕流运动的模拟采用VOF(volume of fluid)方法,该方法可方便地处理自由面的拓扑结构变化和大变形等复杂情况。设控制体单元中含有空气和水,空气的体积分数为αa,水的体积分数为αw,则水的体积分数输运方程为
(3)
体积分数值和应为1,即约束条件为:
αa+αw=1.0
(4)
1.3 边界条件设定
1)空气、水流速度入口:采用气液二相流等效模拟空气和水,通过设定不同的水流入口高度模拟路面积水厚度,空气入口高度根据模型高度和水膜厚度的不同而分别设定。
2)压力出口:轮胎接地区域后端为压力出口,设定相对于参考压力点的流体静压值。
3)壁面:轮胎胎面设定为无滑移条件;计算域侧面和底部路面设定为无剪切力滑移条件,移动速度与水流速度相同。
4)对称面:垂直于对称面的速度分量为0;平行于对称面的速度分量的法向导数为0。
5)初始流场:t=0时刻,整个计算域内充满空气,水体积分数为0,水和空气速度均为0。
在数值求解中,对流项采用二阶迎风差分,耗散项采用中心差分。压力速度耦合方法为PISO,仿真时间步长为0.000 1 s。
2 结果分析与讨论
2.1 滑水模型有效性
当水流作用于胎面的动水压力大于轮胎充气压力时,即发生“滑水”,NASA滑水速度预测方程为
(5)
式中:P为轮胎充气气压,VH为临界滑水速度。由式(5)可预测该轮胎在额定气压240 kPa下的临界滑水速度为98.4 km/h。
表1为10 mm水膜厚度,利用所建滑水分析模型得到的不同水流速度下的胎面动水压力。由表1可知,水流速度为90 km/h的胎面动水压力为220 kPa,小于轮胎额定气压;水流速度为100 km/h时的胎面动水压力为270 kPa,大于轮胎额定气压;水流速度为95 km/h时的胎面动水压力,其值为241 kPa,略大于轮胎额定气压。根据Horne的理论,可认为95 km/h时速度下轮胎发生“滑水”,其速度与NASA预测值误差为3.6%。由表1可知,建立的滑水分析模型与NASA方程结果具有较好的一致性。

表1 速度与动水压力关系
2.2 水流自由液面运动特征
图3为95 km/h速度下利用VOF方法捕捉到的轮胎接地区水流运动过程。t=0.005 s时,水膜和路面一起移动,尚未与轮胎接触;t=0.01 s时,水膜开始与轮胎接触,由于胎面的挤压,形成的楔形水膜进入接地区,并流入花纹沟内;t=0.015 s时,随着水量不断增大,花纹沟排水能力有限,大量水膜向胎面两侧溢散,此时,接地区内的水膜升力使轮胎与路面逐渐分离;t=0.04 s时,轮胎被接地区水膜升力“抬起”,轮胎发生滑水。

图3 轮胎滑水过程自由液面时域Fig.3 Tire hydroplaning process of free surface in time domain graph
2.3 花纹沟内水流特性
由图4可知,在水流尚未进入花纹沟时,主纵沟处的水流因受到楔形区域内积水压力的影响,速度较小;而次纵沟靠近胎侧,因为胎侧阻碍作用较小而形成一个低压区域,楔形区域内的积水沿着胎侧流向轮胎后缘,使得该处的水流速度增加。一旦进入到花纹沟内部,由于接地区域后端与大气相连通,花纹沟两端会形成明显的压力差迫使水流速度急速上升。因为主纵沟两端形成的压力差大于次纵沟两端压力,造成主纵沟内水流速度大于次纵沟内水流速度,加之惯性作用,该态势一直保持下去直至远离轮胎接地区域。其中主纵沟A前端水流平均速度为28 m/s,次纵沟B前端水流平均速度为22 m/s。
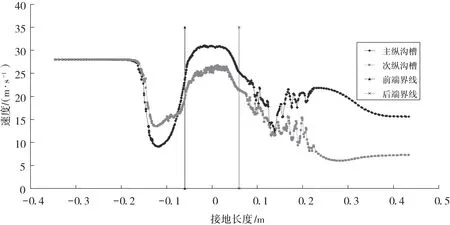
图4 不同花纹沟内水流速度对比(95 km/h)Fig.4 Flow rate for a different groove compared(95 km/h)
3 轮胎滑水性能影响因素分析
3.1 不同水膜厚度对轮胎滑水性能影响
图5示出了水膜厚度分别为3,5,7,10 mm情况下胎面动水压力图。由图5可知,胎面所受动水压力与水膜厚度成正向相关关系。当水膜厚度小于花纹沟深度时,动水压力增长迅速;当水膜厚度等于或大于花纹深度时,动水压力增长缓慢。这主要是因为当水膜厚度小于花纹沟深度时,接地前端楔形区域内水流会更多地流向纵向花纹沟,并能较为通畅地排出,难以形成积水;当水膜厚度接近或大于花纹沟深度时,水流则主要是通过胎侧处排开,受限于花纹沟排水能力的影响,致使大部分水流在楔形区域内聚集而产生明显的动水压力。不同水膜厚度的水流路径及速度矢量如图6。

图5 不同水膜厚度下胎面动水压力(95 km/h)Fig.5 Different tread water pressure under the water film thickness

图6 不同水膜的水流路径及速度矢量(95 km/h)Fig.6 Different water film flow path and velocity vector(95 km/h)
3.2 不同水流速度对滑水性能的影响
依据表1,选择速度为90 km/h和100 km/h两种工况进行接地区水流运动特征的对比分析,如图7。由图7可知,水流速度的改变对接地后端现象不明显,对接地前端则影响较大。相对低速水流,增加水流速度会减小接地前端动水压力沿胎侧方向的分布,也即水流沿胎侧方向流动减小,造成绝大部分水流遇到“障碍”时冲向胎面,对胎面起到一个大的“抬举”力;反观低速水流,在遇到“障碍”时,更多的积水会流向胎侧,有效减缓了水流对胎面的冲击,从而减小胎面受到的动水压力。对接地区花纹沟槽水流运动分析,可以发现,接地区主纵花纹沟的水流速度明显要高于次纵花纹沟。换句话说,在水流速度一定的情况下,改变胎面花纹结构设计是会影响到水流运动,从而对轮胎的滑水性能产生决定性影响。
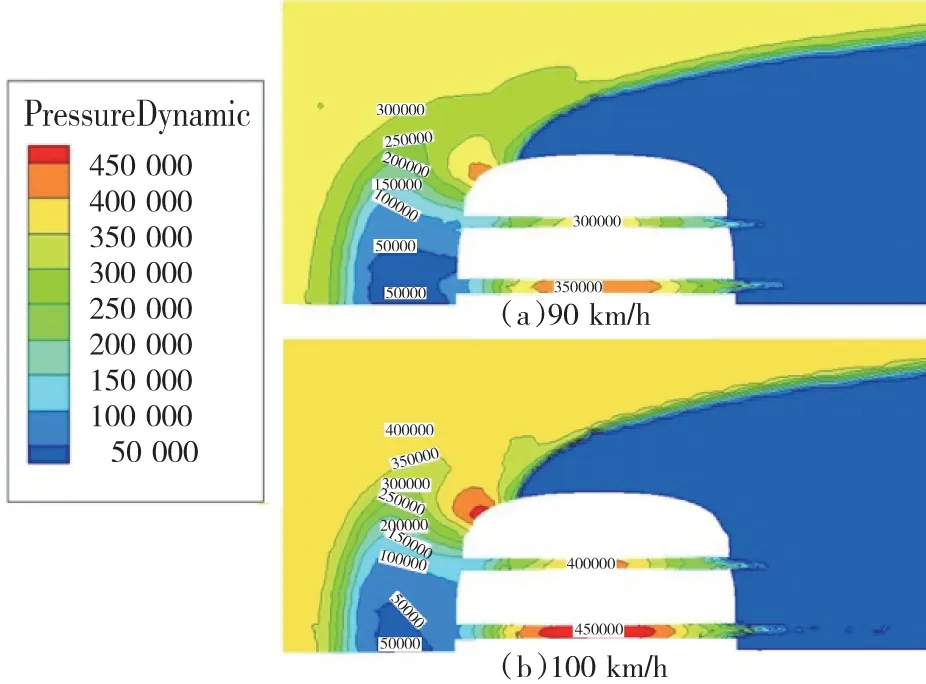
图7 不同速度下接地区水流动水压力对比Fig.7 Comparison of hydrodynamic pressure in the area under different velocity
3.3 纵向花纹结构设计对滑水性能的影响
结合轮胎花纹纵向沟的排水功能,在不牺牲轮胎抓地和转向性能的同时,依据正交试验设计,以纵向花纹沟的宽度、深度和距离胎面中心位置作为设计变量,探究了纵向花纹沟布局对轮胎抗滑水性能的影响,参数设置见图8。为评价不同花纹结构对滑水性能的影响,引入升力系数Cp作为响应指标,如式(6)。压力系数越小,轮胎受到的动水压力越小。方案设计及试验结果见表2。
(6)
式中:pd是作用于胎面的动水压力Pa;p∞是远场静压,取值为0;ρ为流水密度,kg/m3;U∞为水流速度90 km/h。

图8 花纹结构参数设计Fig.8 Pattern design of structure parameters

试验序号因 素宽度W/mm深度D/mm间距L/mm升力系数16.0006.00030.0000.70326.0008.00035.0000.63236.00010.00040.0000.67849.0006.00035.0000.68559.0008.00040.0000.59569.00010.00030.0000.623712.0006.00040.0000.681812.0008.00030.0000.475912.00010.00035.0000.585k10.6710.6890.591k20.6340.5770.634k30.5800.6190.660R0.0910.1210.051主次顺序深度>宽度>间距
利用直观分析法对表2结果进行分析,可得随着花纹纵沟宽度和深度的增加,轮胎胎面受到的压力系数呈明显下降趋势;而纵沟花纹间距的增加,压力系数会出现先减小后增大的趋势;增加接地中央区域花纹沟空间体积能够减小胎面受到的动水压力。由此可以推断花纹纵沟在胎面横向布局存在一个最优的设计,既降低胎面动水压力实现滑水性能的提高的同时又确保轮胎其他性能不降低。在胎面宽度一定的前提下,适当增加纵向花纹沟的宽度和深度有助于提高轮胎的抗滑水性能;纵向花纹沟布置越靠近接地区域中心排水效果越好。通过这三者的优化组合可以提高轮胎花纹的抗滑水性能。
由图9可知,接地区花纹沟沟槽体积较小的方案1,水流不易通过花纹沟,使得接地前端出现大范围的水流低压区域;该区域容易形成积水,即使部分水流能够进入到花纹沟内部,因为花纹沟体积减小从而限制水流通过,花纹沟的排水能力较弱。接地区花纹沟体积大的方案9,因为水流空间宽畅,接地前端水流低压区域较小,水流充分发展,不易形成有效积水,排水能力较好,故水流能够以较高速度通过花纹沟,在接地后端形成明显的两股水流。

图9 不同方案下水流动水压力对比Fig.9 Comparison of flow water pressure in different scenarios
3.4 横向花纹结构设计对滑水性能的影响
考虑到接地区水流运动会对轮胎滑水性能有决定性影响,在轮胎接地印迹长度和宽度不变的条件下,仅仅建立接地区域内纵向花纹为滑水子模型,如图10。设定横向花纹沟深度与纵向花纹沟深度均为8 mm,以横向花纹沟宽度WT、与纵向沟夹角β和横向沟数目N为研究对象;以花纹沟底部动水压力为响应指标,采用正交试验方法对结构参数进行方案设计。模型中采用结构化网格划分,单元最小尺寸为0.05 mm,最大为1 mm。其边界条件设置遵循整体模型,主纵沟入口水流速度为28 m/s,次纵沟入口水流速度为22 m/s,通过监视出口流量和壁面阻力来判定求解是否达到稳定状态。表3给出的正交试验方案及其稳定状态下的动水压力。

图10 滑水分析子模型及局部放大图Fig.10 Partial analysis of hydroplaning models and partial enlargement
对表3进行回归分析,得到动水压力和试验因素的多元线性回归方程为:

表3 横向花纹沟参数正交试验方案及结果
对回归系数进行标准化处理(各试验因素的标准化系数依次为-0.306,-0.304,-0.889),得出横向花纹结构参数对动水压力指标的影响权重,即沟槽数目>沟槽宽度>沟槽角度。在一定程度上来讲,增加接地区域内花纹沟的数目实际上是提高了水流通过量,减少了水流对胎面花纹的动水压力,在一定有效面积的前提下动水压力对胎面花纹的作用力也会相应减小。
为了检验横向花纹沟对实际胎面动水压力的影响,采用小节1.2建立轮胎滑水模型。图11为有无横向花纹沟的轮胎胎面接地区自由液面对比图。从图11中可知,横向花纹沟连通了纵向花纹沟,使得轮胎接地区域内水流方向发生改变,增加胎侧处水流量。通过对胎面动水压力对比发现,带有横向花纹沟的胎面动水压力减小了11 kPa,轮胎临界滑水速度提高了约2.62 km/h。

图11 自由液面对比(90 km/h)Fig.11 Comparison of free surface(90 km/h)
4 结 论
1)CFD数值方法能够实现轮胎发生滑水现象过程中的流场可视化,清晰辨识水流在接地区内流动特征。胎面接地区域动水压力由胎面中央向边缘处递减,接地区域中央花纹沟水流速度明显大于其他位置花纹沟。
2)在一定行驶速度下,水膜厚度对水流运动有直接影响。薄水膜时,路面水流能够顺畅进入花纹沟内;厚水膜时由于“雍水”现象使得水急剧流向胎侧,花纹沟几乎丧失排水能力。同时,增加路面水膜厚度会增加胎面受到的动水压力,降低轮胎发生滑水的临界速度。
3)胎面纵向花纹结构参数及排列布局直接影响着轮胎滑水性能。增加轮胎接地中央区域花纹沟空间体积能够降低胎面受到的压力系数,提高轮胎抗滑水性能;胎面花纹宽度对滑水性能影响较为显著,花纹间距其次,花纹沟深度相对最小。
4)增加接地区域内横向花纹能够降低胎面动水压力。增加接地区域内横向花纹沟能够提高轮胎海陆比,增加接地区域内排水空间,提高胎侧处排水量,实现轮胎抗滑水性能提升。
[1] AGRAWAL S K, HENRY J J.A simple tire deformation model for the transient aspect of hydroplaning[J].TireScienceandTechnology, 1980,8:23-36.
[2] JEONG J Y, JEONG H Y. Hydroplaning simulation of a tire in thin water using fem and an estimation method and its application to skid number estimation[J].InternationalJournalofAutomotiveTechnology, 2013,14(2):325-331.
[3] JENQ S T, CHIU Y S. Hydroplaning analysis for tire rolling over water film with various thicknesses using the LS-DYNA fluid-structure interactive scheme[J].Computers,Materials&Continua, 2009,11(1):33.
[4] 岳宝增,李笑天. ALE有限元方法研究及应用[J].力学与实践,2002,2(2):7-11. YUE Baozeng, LI Xiaotian. Study of the ALE finite element method and its applications[J].MechanicsandEngineering, 2002,2(2):7-11.
[5] 边飞龙,朱有利,杜晓坤,等.基于CFD方法的气动喷丸两相流场特性研究[J].计算机仿真,2015,32(1):264-269. BIAN Feilong, ZHU Youli, DU Xiaokun, et al. Research on performance of two-phase flow field of the pneumatic shot peening based on CFD method[J].ComputerSimulation, 2015,32(1):264-269.
[6] WANG Guolin, ZHOU Haichao, YANG Jian,et al. Study on the influence of bionic non-smooth surface on water flow in antiskid tire tread pattern[J].JournalofDonghuaUniversity(EnglishEdition), 2013,30(4):336-342.
[7] WIES B, ROEGER B,MUNDL R. Influence of pattern void on hydroplaning and related target conflicts[J].TireScience&Technology, 2009,37(3):187-206.
[8] SEIRANGAM S K, KUMAR A,FWA T F. Analyzing effect of tire groove patterns on hydroplaning speed[J].JournaloftheEasternAsiaSocietyforTransportationStudies,2010,8:2018-2031.
[9] 王长建,臧孟炎.复杂花纹子午线轮胎水滑特性仿真研究[J].橡胶工业,2012,58(10):620-624. WANG Changjian, ZANG Mengyan. Numerical investigation of hydroplaning characteristics of tire with 3D complex pattern[J].ChinaRubberIndustry, 2012,58(10):620-624.
[10] 周海超,梁晨,杨建,等.提升轮胎抗滑水性能方法研究[J].机械工程学报,2015,51(8):125-130. ZHOU Haichao, LIANG Chen, YANG Jian, et al. Bionic method for improving tire anti-hydroplaning performance[J].JournalofMechanicalEngineering, 2015,51(8):125-130.
[11] 屈焕成,张荻,谢永慧,等.汽轮机调节级非定常流动的数值模拟及汽流激振力研究[J].西安交通大学学报(自然科学版),2011,45(11):39-44. QU Huancheng, ZHANG Di, XIE Yonghui, et al. Numerical simulation of unsteady flow phenomena and excitation force in control stage of steam turbine[J].JournalofXi’anJiaotongUniversity(NaturalScience), 2011,45(11):39-44.
(责任编辑 朱汉容)
Reserch on Flow Field and Influencing Factors of Tire Hydroplaning Based on CFD Method
ZHOU Haichao1,CHEN Lei1,ZHAI Huihui2,LEI Lili1
(1. School of Automotive & Traffic Engineering, Jiangsu University, Zhenjiang 212013 Jiangsu,P.R.China;2.School of Automotive Engineering, Zhenjiang College, Zhenjiang 212013,Jiangsu,P.R.China)
Tire hydroplaning performance has a decisive influence on vehicle safety and maneuverability, and the pattern structure design parameters directly affect the tire contact area of water movement, which will have a direct impact on tire hydroplaning performance. But due to tire hydroplaning performance test conditions are extremely harsh, and it is difficult to capture the water flow characteristics when hydroplaning occurs. In order to clear the effect of the flow characteristics and pattern structure design parameters on hydroplaning performance when hydroplaning occurs, the hydroplaning analysis model with tire footprint and pattern deformation was established by virtual of the computational fluid dynamics method, and get the flow field distribution features of water film lift, free liquid surface and the groove flow speed. The effects of water film thickness, flow velocity, longitudinal pattern and the cross pattern structure design on hydroplaning performance were analyzed. The results show the water can enter freely the grooves and drainage in the thinner; the circumferential patterns have important influence on tire hydroplaning and adding the number of transverse pattern in footprint can decrease hydrodynamic pressure.
vehicle engineering; tire hydroplaning; tire pattern design; flow field characteristic; simulation analysis
10.3969/j.issn.1674-0696.2017.01.20
2015-11-18;
2016-02-22
中国博士后基金项目(2015M571681);江苏大学高级人才项目启动基金项目(1291120046);江苏省汽车工程重点实验室开放基金项目(CXLX 13_676);江苏大学2015年校级大学生实践创新训练项目(201510299231W)
周海超(1984—),男,河南人,讲师,博士,主要从事车辆动态控制及汽车现代轮胎学方面的研究。E-mail:haichaozhou 999@163.com。
U463
A
1674-696(2017)01-110-07

