基于最大熵原理的顺层边坡地震模糊可靠度分析

龚文惠，钟旭晗，陈训龙，邱金伟，李 逸

(华中科技大学 土木工程与力学学院，湖北 武汉 430074)

基于最大熵原理的顺层边坡地震模糊可靠度分析

龚文惠，钟旭晗，陈训龙，邱金伟，李 逸

(华中科技大学 土木工程与力学学院，湖北 武汉 430074)

考虑地震作用和边坡失稳的模糊性，运用最大熵方法对顺层岩质边坡的地震模糊可靠度进行计算；采用拟静力法，将地震荷载简化成水平方向和竖直方向的惯性力，考虑顺层岩质边坡极限状态的模糊性，建立顺层岩质边坡的模糊极限状态方程；运用最大熵原理，通过数据样本估计出最接近真实情况的概率密度分布，充分利用随机变量的高阶矩信息，推导地震作用下顺层岩质边坡的模糊失效概率的表达式；结合工程实例，通过计算，得出模糊失效概率。计算结果表明：该方法收敛速度快，计算效率高，更加符合工程实际，能广泛运用于实际工程中的模糊可靠性分析。

岩土工程；最大熵原理；地震作用；顺层岩质边坡；模糊可靠度

0 引 言

因地震引发的边坡稳定性问题一直受到岩土工程与地质灾害防治领域的高度关注。20世纪50年代后期，边坡稳定性评价逐步形成了以极限平衡理论居主导、有限元和有限差分等数值方法为辅的定量评价体系。基于确定性理论的这些方法，其缺点是没有考虑岩土体物理力学性质的不确定性，而以概率和统计分析为基础的可靠度分析方法则更能合理地考虑边坡稳定性影响因素(包括地震作用)的不确定性和复杂性[1-2]。

边坡问题的不确定性主要有两种：随机性和模糊性。随机性表现为事件发生条件不充分，条件与结果之间没有必然的因果关系，例如边坡岩土参数的随机性；模糊性表现为研究对象外延不明确，即一个对象是否符合既定概念是难以确定的，例如边坡从“绝对安全”到“完全失效”，其间存在一段中间状态，边坡的失效具有模糊性；对于地震作用，其相互作用力的复杂性通常只能根据经验确定，也具有很强的模糊性。在边坡工程中，模糊性是一种更为深刻、更为普遍的不确定性[3-5]。将概率理论和模糊数学理论相结合，可以较好地处理边坡问题的随机性和模糊性的影响。

国内一些学者针对边坡的随机性和模糊性进行了相关的研究。付士根[6]通过对影响边坡稳定的各个力学参数进行模糊处理，然后应用统计矩点估计方法估计边坡的安全系数均值和可靠度。王广月等[7]综合考虑边坡平面滑动的随机性和模糊性，提出边坡失稳的模糊概率和边坡稳定性模糊随机可靠度的计算方法。吕玺琳等[8]在一次二阶矩法基础上，推导基于瑞典条分法及毕肖普法计算模糊随机可靠度的具体公式。这些方法均是在传统的可靠度计算方法上考虑随机性和模糊性的影响，传统的可靠度计算方法需要依赖大量的统计资料，而且只使用基本变量的均值和方差信息，无法更好地与实际工程相符。

为了使结果更加精确可靠，笔者运用最大熵方法进行可靠度分析。最大熵原理的实质就是，当我们需要对一个随机事件的概率分布进行预测时，我们的预测满足全部已知的条件，而对未知的情况不要做任何主观假设，在这种情况下，概率分布最均匀，预测的风险最小，不仅能考虑样本参数的均值和方差，样本参数的偏度、对称性、峰度和其他高阶中心矩等信息也参与计算，可以更好地拟合出功能函数的概率密度函数，构造“最佳”概率分布，与工程实际更加相符。

笔者通过建立地震作用下顺层岩质边坡的模糊极限状态方程，运用最大熵原理，推导地震作用下顺层岩质边坡模糊失效概率的计算表达式，从而能进行地震作用下的顺层岩质边坡的模糊可靠度分析。

1 模糊极限状态方程

1.1 地震作用下顺层岩质边坡力学分析

基本假定：

1)顺层岩质边坡变形破坏模式为顺层滑移破坏，选取贯穿坡脚到坡顶的软弱结构面为最危险滑动面，如图1。

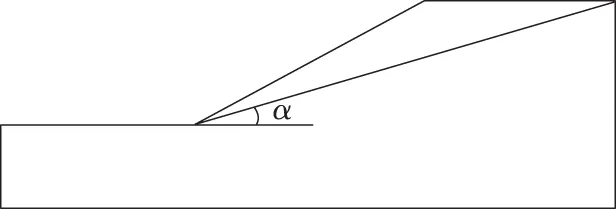
图1 边坡计算断面Fig.1 Slope profile for calculation

2)滑裂面上恰好达到极限平衡状态且满足莫尔-库伦屈服准则。

采用拟静力法，将地震作用简化为水平方向或垂直方向不变的惯性力，根据极限平衡法或有限元强度折减法计算得到边坡拟静力安全系数。水平向地震惯性力可按式(1)计算：

QH=KHCZαiW

(1)

式中：QH为作用于滑动体中心点的水平向地震惯性力；KH为水平向地震系数，按文献[9]采用；CZ为综合影响系数，取0.25；αi为地震加速度分布系数；W为滑动体的重力。

在分析地震作用下的边坡受力中，一般可只考虑水平向地震作用，但对于设计烈度为8、9度的大型工程，则应同时考虑水平向和竖直向的地震惯性力作用。但由于水平向最大地震力与垂直向最大地震力很少同时发生，故对于垂直向地震力建议乘以0.5的系数[9]。垂直向地震惯性力按式(2)计算：

QV=0.5KVCZαiW

(2)

式中：QV为作用于滑动体中心点的竖向地震惯性力；KV为垂直向地震系数，KV=2KH/3。

式中地震加速度分布系数αi的取值如图2[10]，图中，αm在设计烈度为7，8，9度时，分别取为3.0，2.5，2.0。由图2可见，αi是分段线性的，其中H为边坡的坡高，h为滑动体重心到坡底的垂直高度。

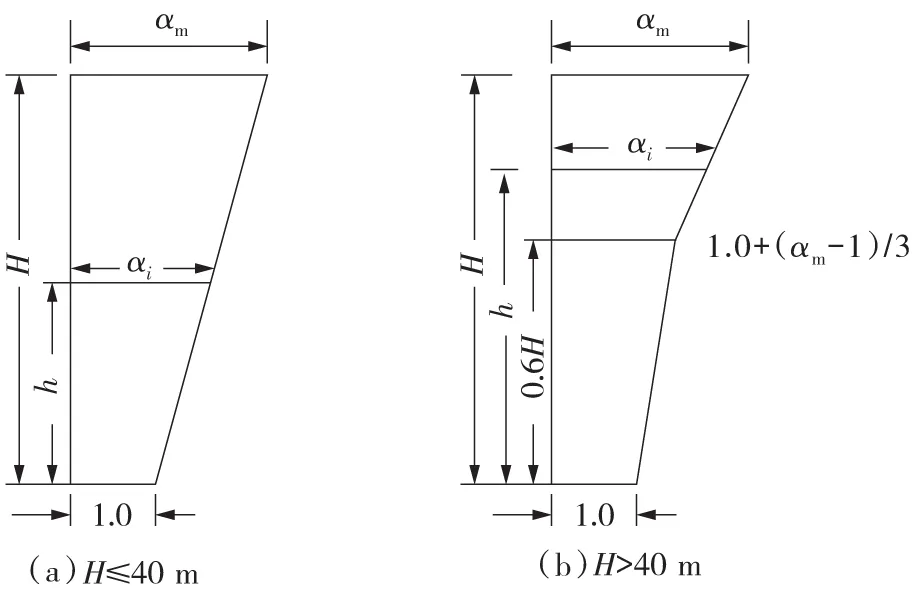
图2 地震加速度分布系数Fig.2 Distribution coefficient of seismic acceleration

根据以上原理考虑地震作用，对顺层岩质边坡滑动体进行如图3的力学分析。图3中，QH为作用于滑动体中心点的水平向地震惯性力，QV为作用于滑动体中心点的竖向地震惯性力，W为滑动体的重力；N为坡面的法向支撑力，T′为切向的摩擦阻力。

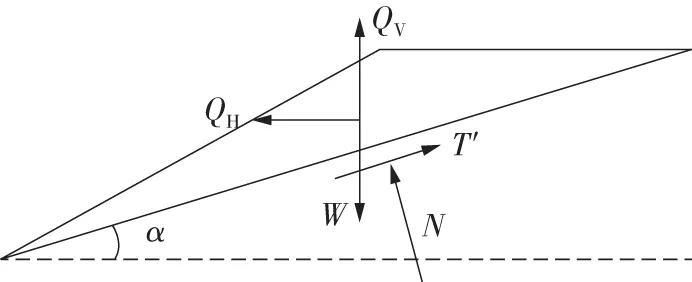
图3 滑动体受力分析Fig.3 Force analysis of sliding block

由图3受力分析，根据静力平衡条件，∑Fx=0，∑Fy=0，可求得边坡下滑力和抗滑力分别为

(3)

式中：c为岩土体的黏聚力；L为滑动面的长度；φ为岩土体的内摩擦角。

1.2 边坡稳定的功能函数

根据极限平衡理论，边坡稳定安全系数FS在此处定义为抗滑力与下滑力之比。根据实际工程特点及边坡的重要性，一般要求FS≥1.2，笔者取FS=1.2为临界状态。当FS>1.2时，边坡处于稳定状态；当FS<1.2时，边坡处于不稳定状态。

边坡的稳定安全系数的表达式为

(4)

(5)

(6)

1.3 模糊极限状态方程的建立

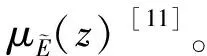
边坡失稳的模糊随机事件可表示为

(13)

于是式(13)为边坡破坏失稳的功能函数，以式(11)和式(12)为补充条件，根据式(6)可得本文采取的计算模型在地震作用下的等效功能函数为

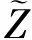
1.2-X3

(14)

式中：黏聚力c和内摩擦角φ为随机变量；X3为新的随机变量。

为表示边坡极限状态的模糊性，引入一个在“零”附近的不确定区间，即模糊临界区间，以此代替传统极限状态临界点。模糊临界区间用[a,b]表示(a，b为待定常数)，分析计算时，[a,b]可近似地取以“零”点为对称的区间，即a=-b。将隶属函数取作降半梯形分布，即：

(15)

由式(11)和(12)可得，X3服从区间(a，b)上的均匀分布，其概率密度函数和累积分布函数分别为

(16)

(17)

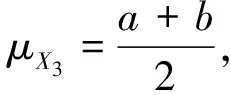
因此，地震作用下顺层岩质边坡的模糊极限状态方程为

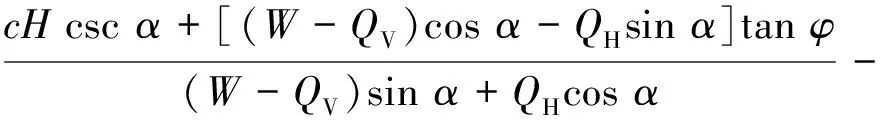
(18)

2 最大熵原理及求解模糊可靠度方法

1948年，SHANNON将热力学熵的概念引入信息论中，首次提出信息熵的概念，把熵作为一个随机事件的“不确定性”或信息量的量度，从而奠定现代信息论的科学理论基础[12-14]。

2.1 最大熵原理

对于某一特定的信息源，其信息熵只有一个。不同的信息源，其信息熵是不同的。SHANNON自定义信息的数学期望为信息熵，即为信息源的平均信息量，SHANNON引入下列函数：

(19)

若随机事件服从概率密度为fX(x)的连续分布，SHANNON熵为

(20)

在已知的信息附加约束条件下使信息熵最大，所得到的概率分布是最符合实际情况的，由此可得到一种构造“最佳”概率分布的途径。当数据或条件不够时，最大熵原理的意义就在于，在所有可行解中，满足一定约束条件时，应该选择熵最大的一个。因为熵可以表示一个系统的不确定程度，此时的解包含的主观成分最少，因而是最客观的[15]。

将随机变量X的前m阶原点vXi(i=0，1，…，m)作为约束条件，即在下列条件下使式(20)取到最大值：

(21)

随机变量X的中心矩为

i=0，1，…，m

(22)

式中：μX=vX1为X的均值。

利用Lagrange乘子法，建立拉格朗日函数如式(23)：

(23)

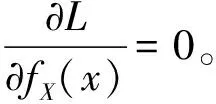
整理后可得最大熵概率密度函数为

(24)

应用约束条件可以得到λ0，λ1，…，λm所满足的方程：

(25)

为了便于数值求解，将式(25)改写为

(26)

为了便于建立优化函数表达式，令

(27)

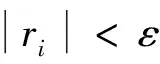
2.2 模糊可靠度的求解方法

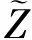
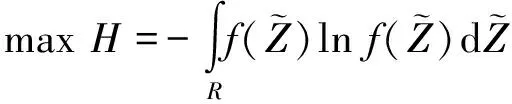
(28)

约束条件为

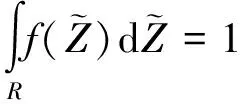
(29)

(30)

(31)

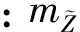
(32)

则边坡失稳的模糊失效概率为

(33)

因此，只要求得拉格朗日乘子λ0，λ1，…，λm，利用相关数学程序实现，就可以求得边坡的模糊失效概率。

3 算例分析

3.1 工程概况

以文献[16]的边坡为例，如图4，地震设防烈度为8度，依据有关试验资料进行统计，顺层岩质边坡的有关参数如表1。

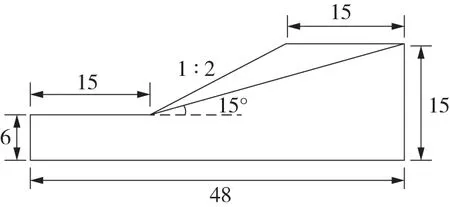
图4 边坡计算模型(单位：m)Fig.4 Slope calculation model

岩体参数重度γ/(kN·m-3)黏聚力c/kPa平均值标准差内摩擦角φ/(°)平均值标准差参量2022212．0715451．21

3.2 可靠度计算

则取值。

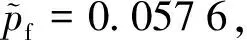
为了说明基于最大熵方法可靠度分析结果的可靠性，采用蒙特卡洛法进行验证。地震作用下顺层岩质边坡的模糊可靠度的蒙特卡洛法和本文方法计算结果进行比较，如表2。

表2 模糊可靠度计算结果

3.3 结果对比分析

根据计算结果，可以看出，考虑极限状态的模糊性的影响后，边坡失效概率比不考虑模糊性时的计算结果大，这是符合理论与实际的，两者误差为7.3%，说明了考虑极限状态的模糊性在保证边坡工程安全方面的重要性。

运用最大熵原理计算出的模糊失效概率和可靠度指标与蒙特卡洛法模拟100万次的计算结果比较接近，说明利用最大熵原理进行可靠度计算的结果具有一定的精度，有实际应用价值。在计算过程中，最大熵方法的收敛速度明显优于蒙特卡洛法，具有较高的计算效率。

3.4 岩体力学参数对边坡模糊可靠度的影响

通过改变顺层岩质边坡岩体的主要物理力学参数即内摩擦角和黏聚力值，进一步验证最大熵方法的可行性，可以得到内摩擦角和黏聚力与模糊失效概率的关系曲线如图5，以及内摩擦角和黏聚力与可靠度指标的关系曲线如图6。

图5 内摩擦角φ和黏聚力c与模糊失效概率pf关系曲线Fig.5 Relationship between angle of friction φ and cohension c and fuzzy failure probability pf

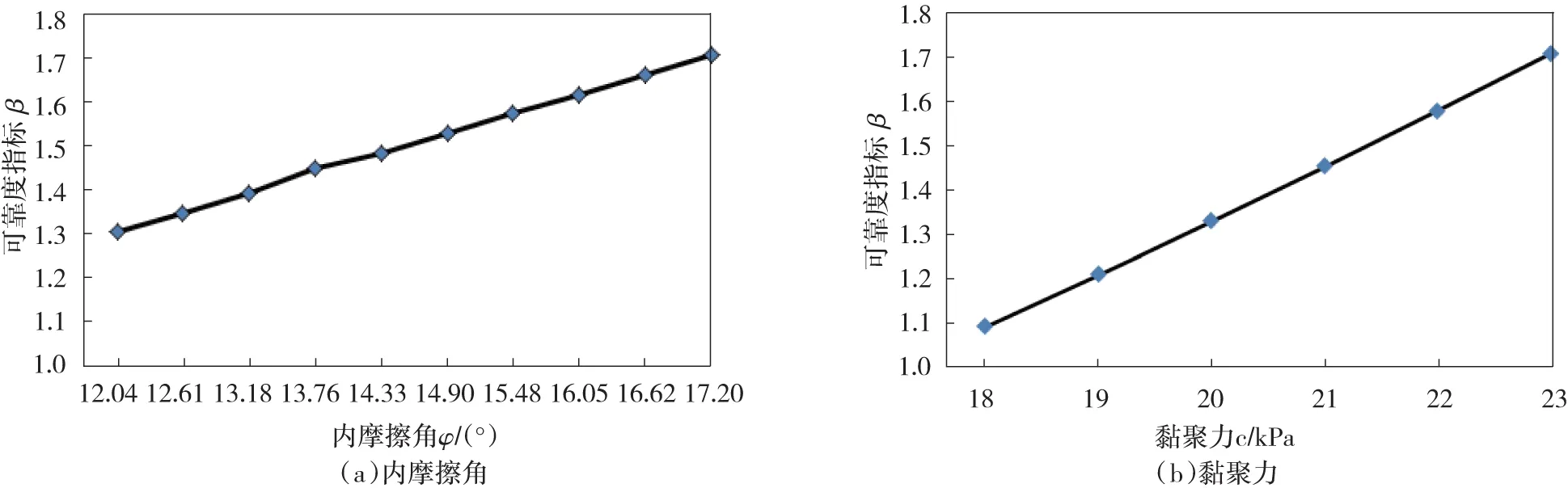
图6 内摩擦角φ和黏聚力c与可靠度指标β关系曲线Fig.6 Relationship between angle of friction φ and cohension c and reliability index β

从图5、图6中可以看出，边坡岩体力学参数内摩擦角和黏聚力对地震作用下顺层岩质边坡的模糊可靠度有很大的影响，内摩擦角和黏聚力越大，边坡的模糊失效概率越低，可靠度指标越高。通过改变参数进行计算和对比，可以看出最大熵方法在计算地震作用下顺层岩质边坡的模糊可靠度的实用性和可靠性。

最大熵方法在求解计算时克服了传统可靠度计算方法中只考虑随机变量均值和方差的缺陷，在计算过程中考虑样本的均值和方差外，它的偏度、对称性、峰度和其他高阶中心矩等信息也参与计算，从而使得结果更加合理可靠，精度更高。

4 结 论

将模糊理论与最大熵原理结合，充分利用高阶矩信息，计算顺层岩质边坡在地震作用下的模糊可靠度。结合具体算例，得出以下结论：

1)边坡工程由于其模糊性和随机性这两种不确定性广泛存在，忽略任何一种都将使边坡的稳定性分析结果偏离实际。模糊性对边坡的可靠度有较大的影响，常规的可靠度计算方法所求的失效概率偏小，不利于判断边坡的安全状态。因此，必须特别重视模糊性对边坡稳定的影响。

2)运用最大熵方法进行可靠度计算时，与蒙特卡洛法相比，收敛速度快，计算效率高。对于基本随机变量可以不考虑其实际概率分布，比传统的方法更有应用价值。

3)最大熵方法充分地利用样本参数的各阶矩、偏态系数、峰度系数等信息，直接反映了真实信息，更好地拟合出功能函数的概率密度函数，更加符合工程实际。本文方法采用的数据直接来源于样本，减少了对已有数据和经典概率分布的依赖，为边坡的模糊可靠性分析开拓新的思路。

[1] 贡金鑫.工程结构可靠度计算方法[M].大连：大连理工大学出版社，2003：13-21. GONG Jinxin.ComputationalMethodsforReliabilityofEngineeringStructures[M]. Dalian: Dalian University of Technology Press, 2003：13-21.

[2] 张明.结构可靠度分析——方法与程序[M].北京：科学出版社，2009：15-22. ZHANG Ming.StructuralReliabilityAnalysis:MethodsandProcedures[M]. Beijing: Science Press, 2009：15-22.

[3] 王亚军，吴昌瑜，任大春，等.岩土工程非确定理论研究与应用[M].北京：科学出版社，2014：7-14. WANG Yajun, WU Changyu, REN Dachun, et al.Non-deterministicTheoryResearchandApplicationofGeotechnicalEngineering[M]. Beijing: Science Press, 2014：7-14.

[4] 舒苏洵，龚文惠.考虑参数空间变异性的边坡模糊随机可靠度分析[J].华中科技大学学报(自然科学版)，2014，42(9)：93-97 SHU Suxun, GONG Wenhui. Fuzzy random reliability analysis of slopes considering spatial variability of soil parameters[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition), 2014，42(9)：93-97.

[5] 龚文惠，王元汉，郑俊杰.基于模糊理论的膨胀土路基沉降的可靠度分析[J].华中科技大学学报(自然科学版)，2008，36(3)：51-53. GONG Wenhui, WANG Yuanhan, ZHENG Junjie. Reliability analysis on settlement of expansive soil roadbed based on fuzzy theory[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition)，2008，36(3)：51-53.

[6] 付士根.基于模糊随机可靠性的边坡稳定性评价[J].中国安全生产科学技术，2012，8(8)：99-101. FU Shigen. Stability assessment of opencast mines slope based on fuzzy stochastic reliability[J].JournalofSafetyScienceandTechnology, 2012，8(8)：99-101.

[7] 王广月，刘健，王有志.岩质边坡平面滑动的模糊可靠度分析[J].岩土力学，2005，26(增刊1)：283-286. WANG Guangyue, LIU Jian, WANG Youzhi. Analysis of fuzzy reliability for plane sliding of slope[J].RockandSoilMechanics, 2005，26(Sup1)：283-286.

[8] 吕玺琳，钱建固，吕龙，等.边坡模糊随机可靠性分析[J].岩土力学，2008，29(12)：3438-3441. LV Xilin, QIAN Jiangu, LV Long, et al. Fuzzy stochastic reliability analysis of slopes[J].RockandSoilMechanics, 2008，29(12)：3438-3441.

[9] 龚文惠.土力学[M].武汉：华中科技大学出版社，2013：166-167. GONG Wenhui.SoilMechanics[M]. Wuhan: Huazhong University of Science & Technology Press, 2013：166-167.

[10] 吕擎峰，殷宗泽，王叔华，等.拟静力法边坡稳定分析的改进[J].岩土力学，2005，26(增刊1)：35-38. LV Qingfeng, YIN Zongze, WANG Shuhua, et al. Improvement of pseudo-static method for slope stability analysis[J].RockandSoilMechanics, 2005，26(Sup1)：35-38.

[11] 李虎生，叶黔元.陡峭岩石边坡随机-模糊可靠度算法[J].岩土工程学报，2006，28(8)：1019-1022. LI Husheng, YE Qianyuan. Calculation of random-fuzzy reliability of steep slopes[J].ChineseJournalofGeotechnicalEngineering, 2006，28(8)：1019-1022.

[12] 王宇，张慧，贾志刚.边坡工程可靠性分析的最大熵方法[J].工程地质学报，2012，20(1)：52-53. WANG Yu, ZHANG Hui, JIA Zhigang, The maximum entropy method for reliability analysis of slope engineering[J].JournalofEngineeringGeology, 2012，20(1)：52-53.

[13] SOBCZYK K, TREBICKI J. Approximate probability distributions for stochastic systems: maximum entropy method[J].ComputerMethodsinAppliedMechanicsandEngineering, 1999，168(1)：91-111.

[14] PANDEY M D. Direct estimation of quantile functions using the maximum entropy principle[J].StructuralSafety, 2000，22(1)：61-79.

[15] 张道兵，杨小礼，朱川曲，等.基于最大熵原理与最优化方法的隧道衬砌结构可靠度分析[J].中南大学学报(自然科学版)，2012，43(2)：664-666. ZHANG Daobing, YANG Xiaoli, ZHU Chuanqu, et al. Structural reliability analysis of tunnel lining based on maximal entropy principle and optimization method[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2012，43(2)：664-666.

[16] 邱金伟，龚文惠，陈训龙，等.基于盲数理论和响应面法的边坡稳定性分析[J].计算力学学报，2014，31(增刊1)：97-99. QIU JInwei, GONG Wenhui, CHEN Xunlong, et al. Slope stability analysis based on blind data theory and response surface method[J].ChineseJournalofComputationalMechanics, 2014，31(Sup1)：97-99.

(责任编辑 谭诸凯)

Seismic Fuzzy Reliability Analysis of Bedding Slope Based on the Maximum Entropy Principle

GONG Wenhui, ZHONG Xuhan, CHEN Xunlong, QIU Jinwei, LI Yi

(School of Civil Engineering & Mechanics, Huazhong University of Science and Technology,Wuhan 430074, Hubei, P.R. China)

The maximum entropy method was applied to calculating the seismic fuzzy reliability of bedding slope with the seismic action and the fuzziness of slope instability considered. By pseudo-static method, the seismic load was simplified into horizontal and vertical inertial force and the fuzzy limit state equation was established with the fuzziness of the limit states considered. The maximum entropy principle was applied to estimate the probability density distribution which was closest to reality and the higher order moments of the random variable information were fully used to calculate the fuzzy failure probability of bedding rock slope under seismic load. An example was analyzed and the fuzzy failure probability was calculated. The results from a case study indicate that the method with a fast convergence and a high calculation efficiency which more complies with engineering practice can be widely used in fuzzy reliability analysis of practical engineering.

geotechnical engineering; maximum entropy principle; seismic action; bedding rock slope; fuzzy reliability

10.3969/j.issn.1674-0696.2017.01.11

2015-10-19；

2015-12-08

国家自然科学基金项目(51278217)

龚文惠(1966—)，女，湖北英山人，教授，博士生导师，主要从事岩土力学、地基处理和边坡稳定方面的研究。E-mail: gwh 87806869@163.com。

陈训龙(1989—)，男，安徽安庆人，博士研究生，主要从事岩土工程可靠度方面的研究。E-mail：chenxl 1989@hust.edu.cn。

TU 443

A

1674-0696(2017)01-058-06