土体剪胀特性对土质边坡体系稳定性的影响

陈 曦，张训维，2，苗姜龙，王冬勇

(1.北京交通大学 土木建筑工程学院，北京 100044；2.中国海外工程有限责任公司，北京 100048)

土体剪胀特性对土质边坡体系稳定性的影响

陈 曦1，张训维1，2，苗姜龙1，王冬勇1

(1.北京交通大学 土木建筑工程学院，北京 100044；2.中国海外工程有限责任公司，北京 100048)

基于数值算例，研究了土体剪胀性对土质边坡以及边坡体系稳定性的影响，对比了两种关于剪胀角对边坡稳定性影响的不同观点，采用有限元强度折减法和重力加载法对两种不同方法进行验证。结果发现：有限元强度折减法在进行非关联塑性土质边坡稳定性分析时存在局限性；只有在折减的过程中满足剪胀角小于内摩擦角的条件，强度折减法的结果才是有效的。此外，针对把剪胀角近似取为0°是一种的偏于安全的做法的观点开展研究，对有抗滑桩加固的边坡体系进行研究后发现：剪胀角越小，抗滑桩的变形越小，作用在桩身上的最大土压力也越小，表现出土体更加容易“流过”桩体的特点。因此从边坡安全系数角度考虑，把剪胀角近似取为0°可以得到最小的安全系数，是一种的偏于安全的做法，但是从抗滑桩设计的角度考虑，又是一种偏于不安全的做法。建议在实际边坡工程中具体问题具体分析，合理考虑剪胀角的取值。

岩土工程；剪胀角；边坡体系；抗滑桩；安全系数；有限元强度折减法

0 引 言

土在剪切过程中，所呈现出的体积增大或缩小的性质统称为土的剪胀性。例如，密砂或超固结土在剪切过程中通常呈现出先体积剪缩后体积膨胀的特点，而松砂或正常固结土在剪切过程中主要呈现剪缩性。

尽管剪胀性对土体的受力和变形影响显著[1]，迄今为止有关剪胀性对土质边坡或土质边坡体系稳定性影响方面的研究还十分有限。例如，传统的极限平衡法采用的是相关联流动法则(即剪胀角等于内摩擦角，φ=φ)，已有试验结果表明这种简化会高估土体的剪胀作用，是一种偏于不安全的做法；另一种常见的做法是将非关联流动法则中的非零值剪胀角近似取为0°(即完全忽略土体剪胀性)，普遍观点认为这是一种保守的做法。例如，张培文等[2]基于Drucker-Prager(DP)，Mohr-Coulomb (MC)和von Mises强度准则对非关联塑性流动(φ≠φ)条件下剪胀角对边坡稳定性的影响进行了研究，得到边坡的安全系数随着剪胀角增加而增大的结论，并认为在工程应用中应该考虑剪胀性和屈服准则的影响。蒋青青等[3]分析了不同工况下剪胀角与边坡安全系数的关系，认为安全系数并不随剪胀角的增加而增大，而是随着剪胀角呈现出先增大后减小的抛物线样式。可见，关于剪胀角对安全系数影响目前仍存在着不同认识。此外，LEE Fook-Hou等[4]对将非零值剪胀角近似取零的“保守”做法提出质疑，认为剪胀角越小未必一定会得到保守结果。

针对上述不同的观察，笔者采用ABAQUS软件对边坡以及边坡挡土体系开展数值模拟和分析，力求获得更加可靠的结论。

1 剪胀角与非关联塑性流动法则

剪胀角是描述土体剪切过程中体积变化率的物理量。在经典弹塑性力学中，可引入一个塑性势面函数G来区别屈服面函数F，通过塑性势面来规定塑性流动方向[5]。经典弹塑性力学中，应力应变关系可表示为[6]

dσ=Depdε=(De-Dp)dε

(1)

Dp=DebaTDe/(aTDeb-cTh)

(2)

式中：dσ和dε分别为应力增量和应变增量；De，Dp，Dep分别为弹性、塑性和弹塑性本构矩阵；a,b分别为屈服面F和塑性势面G的法向矢量；c为F对内部状态变量q(q=dλh，其中dλ为塑性乘子增量)的导数。

矢量a,b可表示为：

a=∂F/∂σ

(3)

b=∂G/∂σ

(4)

c=∂F/∂q

(5)

a=b对应关联塑性流模型，所得Dep为对称矩阵；而a≠b对应非关联塑性流模型，所得Dep为非对称矩阵。由于非关联塑性流模型会导致非对称的刚度矩阵，线性求解时也需要选择非对称的线性求解方法。

对于Mohr-Coulomb模型，用剪胀角φ替换屈服面函数F中的内摩擦角φ可获得塑性势面函数G，因此通过判断φ和φ的关系也可判定Mohr-Coulomb模型的塑性流动特征。

2 有限元强度折减法及其应用局限

极限平衡法和有限元强度折减法已经被广泛用于岩土稳定性分析，但相比极限平衡法，有限元强度折减法更容易处理非关联塑性的岩土工程问题，因此笔者采用有限元强度折减法来评估剪胀角对岩土体系稳定性的影响。

需要指出的是，有限元强度折减法还存在若干问题有待解决。比如：①模型的局限。目前强度折减法主要基于线性Mohr-Coulomb模型或者是线性Drucker-Prager模型[7]，对于更为复杂的模型(如Hoek-Brown模型或临界状态模型)还不能直接应用；②计算量较大。以至于强度折减法在三维岩土工程问题的应用有限[8]；③不能得到多斜坡岩土体所有斜坡完整的安全系数演化曲线[9](即只能得到所有斜坡安全系数的最低公共包络线)；④剪胀角的局限。通常采用两个极端的处理，要么近似采用相关塑性流动法则，要么将剪胀角近似取为0。

如何解决上述几个问题还有待进行深入研究。笔者针对第4个问题采用具体算例进行分析研究。

3 均质土坡稳定性分析

算例1为一个均质土坡的经典算例[10]。图1为边坡的有限元网格划分，土体的弹塑性力学参数见表1。土体仅具有关联塑性流，采用极限平衡法获得的安全系数为1.0。

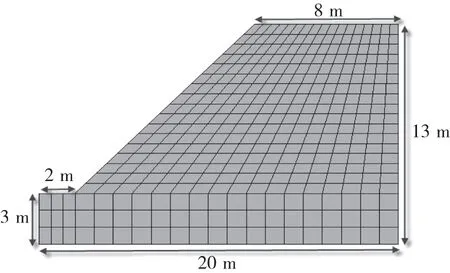
图1 均质土坡有限元网格划分Fig.1 Finite element mesh of homogeneous soil slope

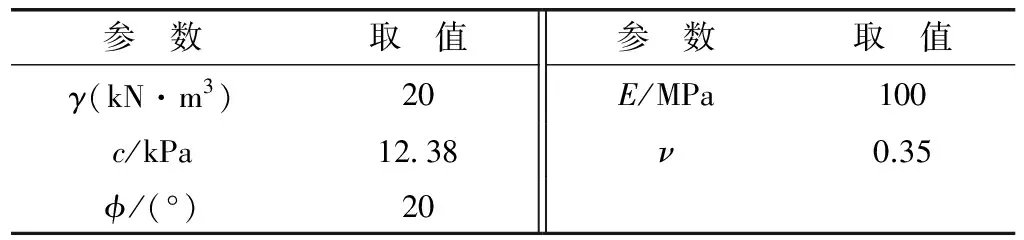
参 数取 值参 数取 值γ(kN·m3)20E/MPa100c/kPa1238ν0．35ϕ/(°)20

3.1 基于强度折减法获得的边坡安全系数

采用强度折减法进行边坡稳定性分析时，需要设定强度折减因子的搜索范围，根据指定的强度折减因子序列对土体的抗剪强度指标c和φ进行折减，直至达到边坡失稳破坏[8]。

图2为剪胀角影响下安全系数的变化曲线。

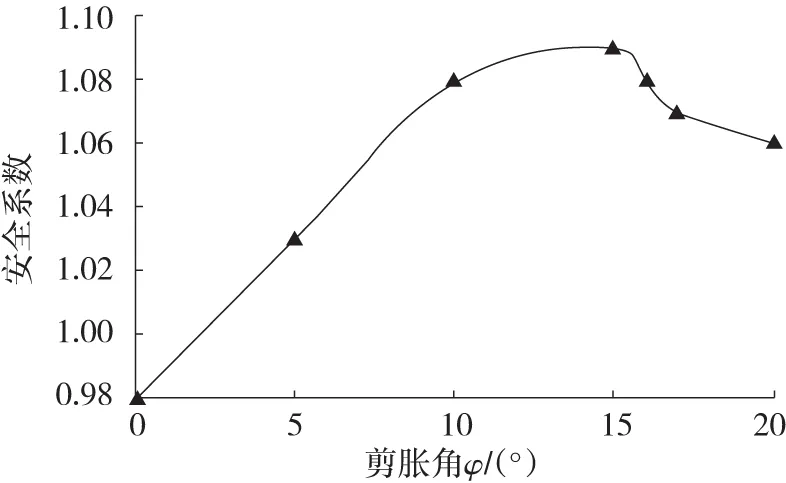
图2 采用强度折减法时获得的安全系数变化曲线Fig.2 Variation curve of FOS obtained by using strength reduction method

由图2可看出：随着剪胀角的增加，安全系数呈现出先增加后减小的抛物线样式，这个变化模式与蒋青青等[3]的计算结果相似，并在剪胀角φ=15°时安全系数达最大，为1.09。

3.2 基于重力加载法获得的边坡安全系数

采用重力加载法时，土体强度参数(即黏聚力和内摩擦角)保持不变，不断增加重力加速度或土体自重直至边坡失稳。图3为采用重力加载法获得的安全系数变化曲线。

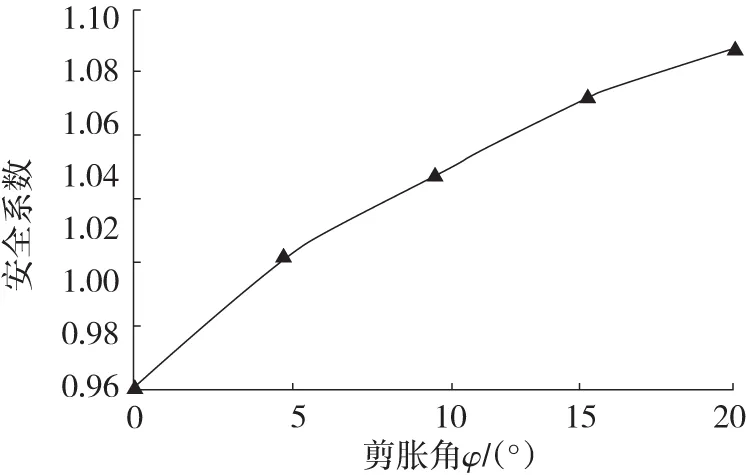
图3 采用重力加载法时获得的安全系数变化曲线Fig.3 Variation curve of FOS obtained by using gravity loading method

图3中，当采用重力加载法时，边坡的安全系数随着剪胀角的增加而逐渐增大，这便获得了与张培文等[2]相似的分析结果。当然图2和图3的曲线不可能都正确。进一步分析可知，图2中强度折减法所获得的安全系数曲线先增加后降低的原因在于：强度折减过程中，剪胀角φ保持不变，c和tanφ不断折减，折减初期还能满足φ<φr，但随着折减的进行，最终出现了剪胀角大于内摩擦角(即φ>φr)的情况。众所周知，对于真实岩土材料，不会出现内摩擦角小于剪胀角的情况。从图2可以看出，剪胀角等于15°时，安全系数曲线出现峰值，约为1.09。

因此，为了确保强度折减法计算结果有效，至少应满足式(6)：

φr=arctan(tanφ/τSRF*)≥φ

(6)

式中：τSRF*为搜索到安全系数时所对应的强度折减因子(且τSRF*=τFOS)。当τFOS=τSRF*=1.09时，φr=18.46°>φ=15°。当剪胀角大于等于15°时，如果继续进行折减，将会出现φr<φ的情况，从而揭示了剪胀角超过15°之后安全系数会呈现下降的原因(图2)。如果采用重力加载法，内摩擦角和剪胀角始终保持不变，且满足φ>φ，不会出现剪胀角大于内摩擦角的情况。

总之，随着剪胀角的增加，边坡安全系数应随剪胀角的增加而增加(图3)，印证了“将非零值剪胀角近似取为零会获得更加保守设计”的观点。

4 剪胀角对土坡体系稳定性的影响

图4为一无限长土质边坡及有限元网格划分。该边坡坡高10 m，坡度1∶1.5，采用抗滑桩对其加固，桩底嵌入岩层或稳定地层，桩距坡角水平距离为7.5 m，桩长L=15.5 m，桩径D=0.8 m。由于抗滑桩的存在，本模型不宜简化为平面应变问题，最好采用三维建模。根据对称性，取模型一半为研究对象，土体、桩以及接触面所采用模型参数如表2。

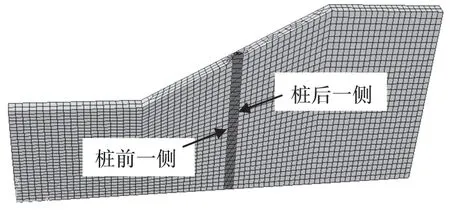
图4 土坡体系的有限元网格划分Fig.4 Finite element mesh of soil slope system

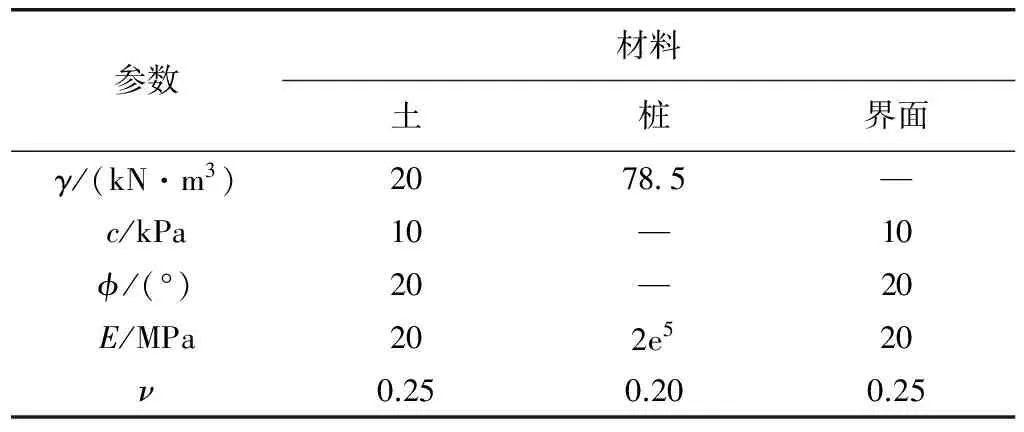
参数材料土桩界面γ/(kN·m3)20785—c/kPa10—10ϕ/(°)20—20E/MPa202e520ν0．250．200．25

土体为关联塑性流条件下获得的安全系数分别为1.55(FLAC3D软件)和1.56(Cai和Ugai)[11]。可见，不同方法获得的安全系数相差不大。由于重力加载法对本算例不适用，只采用强度折减法对该例题进行分析。

由式(6)可知，φr=arctan(tan 20°/1.56)=13.13°，可见剪胀角的取值不能超过13.13°，这里将剪胀角的变化范围限定在10°以内。已有实验数据表明，真实岩土材料的剪胀角通常比内摩擦角要小很多[1]。孔位学等[12]根据滑移线场理论验证了剪胀角在非关联流动条件下剪胀角应该取φ/2的结论；康亚明等[13]则建议在非关联塑性流条件下，一般砂土或黏土应对剪胀角进行折减，并认为剪胀角可取内摩擦角的1/3～1/2，但如此取值并没有理论支持。

为研究剪胀角对边坡体系稳定性和受力的影响，笔者把剪胀角10°以内的取值分成5组，分别为0°，3°，5°，8°和10°，并且规定对非关联塑性土体进行强度折减时，剪胀角保持不变。

4.1 边坡体系稳定性和安全系数分析

判定边坡是否发生失稳破坏的准则主要有3种，即是否具有连续贯通的塑性(滑裂)区，边坡特征点是否发生位移突变以及非线性迭代求解是否不收敛[14]。

笔者采用非线性迭代不收敛作为判定边坡失稳的准则，但需要排除非线性迭代不收敛的其他影响因素(如线性迭代不收敛或外载过大致使系统不平衡等)。采用强度折减法获得的安全系数随剪胀角的演化曲线如图5。

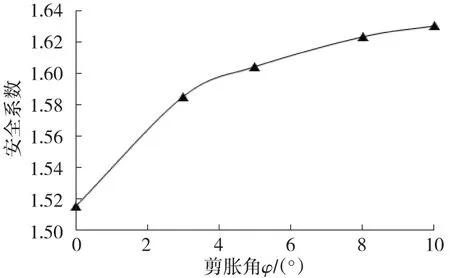
图5 剪胀角变化时安全系数的演化曲线Fig.5 Variation curve of FOS with dilation angle

由图5可看出，边坡安全系数随剪胀角减小而降低，剪胀角从φ=10°下降到φ=0°时，安全系数则从1.630下降到1.515，下降幅度约为8%，并且越接近0°时下降幅度越明显。可见，剪胀角对抗滑桩加固的边坡体系的影响也较为明显，并且仅从安全系数方面考虑，把剪胀角近似取为0°时安全系数最小，确是一种保守的做法。

4.2 滑坡时抗滑桩的变形分析

图6展现了抗滑桩的变形特征以及不同剪胀角条件下抗滑桩桩身的变形曲线。滑坡发生时，抗滑桩上部产生了弯曲变形，而下部由于锚固作用使得变形相对较小。

由图6可知，随着剪胀角的降低，桩身变形量也逐渐降低。φ=10°时桩顶变形量最大，约为8.217×10-2m；φ=0°时桩顶变形量最小，约为6.083×10-2m。很明显，土体剪胀角较小时，作用在桩身上的力也较小，或者也可说剪胀角相对较小的土体表现出更加容易“流过”桩体的特征。

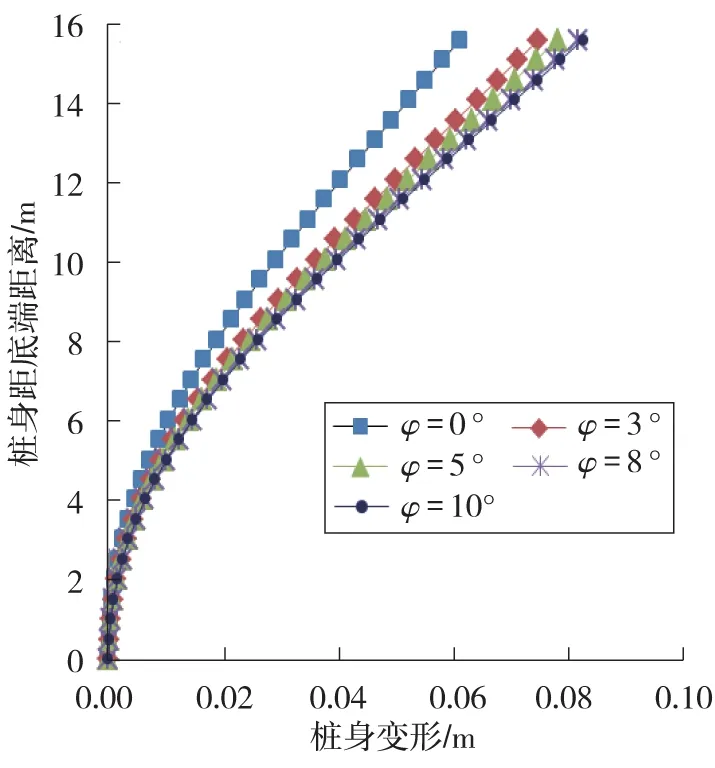
图6 桩身变形随剪胀角的变化曲线Fig.6 Deformation curves of pile shaft with dilation angle

4.3 滑坡时抗滑桩受力分析

进行抗滑桩设计时，需要对桩身土压力(即接触压力)进行分析。为研究桩前(坡下位置)、桩后(坡上位置)以及桩侧所受到的土压力，在桩前、桩后和桩侧沿桩长由上向下每隔1 m提取一个点，桩前、桩后和桩侧位置如图7。

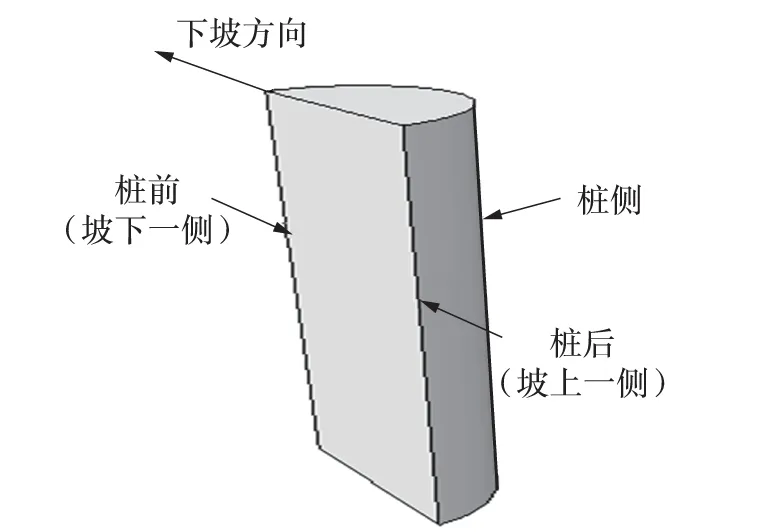
图7 抗滑桩桩前、桩后和桩侧位置示意Fig.7 Schematic diagram of anti-slide pile with front, side and rear surface

4.3.1 桩侧受力分析

图8是剪胀角变化条件下桩侧压力分布。图8中，从桩顶自上向下，作用在桩身上的力呈现出不同的变化阶段，即逐渐增大段(对应图8中的15.5～6.0 m)、基本恒定段(对应图8中的6.0～1.3 m)和逐渐减小段(对应图8中的1.3～0 m)。

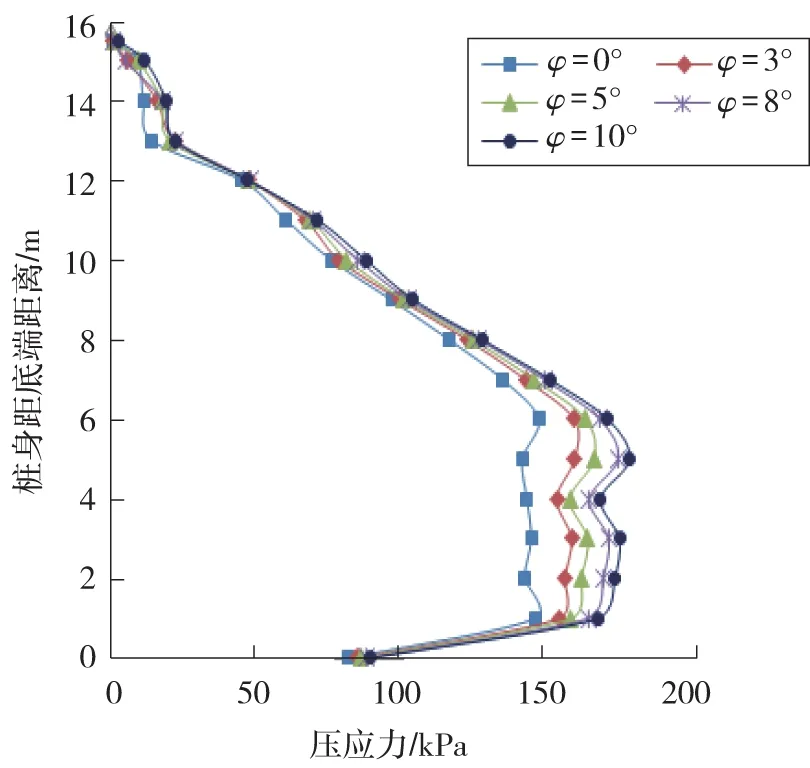
图8 剪胀角变化条件下桩侧压力分布曲线Fig.8 Earth pressure distribution curves along one side of pile shaft with dilation angle

笔者将坡体沿桩身划分为3个分段，即上层滑动段、中层过渡段和下层的准嵌固段(桩底嵌岩点除外)，如图9。上层滑动段大约为4倍桩径(4D)的深度，底层准嵌固段深度大约为4～4.5 m，这里把下层变形量很小的一段定义为准嵌固段。此外，随着剪胀角的增加，抗滑桩桩侧土压力也有所增加，φ=0°时桩侧土压力分布值相对最小，且沿桩长土压力最大值约为147.36 kPa，而φ=10°时桩侧土压力分布值相对最大，且沿桩长土压力最大值约为178.64 kPa。

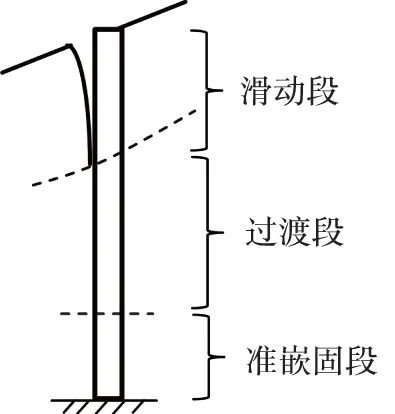
图9 沿桩身坡体分区Fig.9 Partition of slope along pile shaft

4.3.2 桩后受力分析

桩后土压力分布要比常规分析假设的桩后主动土压力要复杂得多，如图10。按图9中的桩身区段划分对桩后土压力分布进行受力分析。

对于下部准嵌固段，准嵌固段内位置靠上的作用点受拉程度大于靠下位置的作用点，因此土压力分布随深度增加而增加；自桩顶向下大约4D范围为滑动段，此深度范围内土压力分布也较为复杂，作用在其上的“主动土压力”基本上随剪胀角的增大而增大，主要是因为剪胀角越小，土越容易“流过”桩体，或者说，桩体对土的“阻挡”作用越小，作用在桩体上的土压力也就越小。过渡段内土压力分析也很复杂。在上层滑动土体的作用下桩身产生弯曲变形。

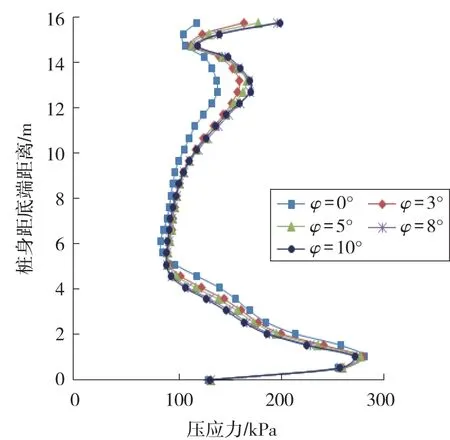
图10 剪胀角变化条件下桩后压力分布曲线Fig.10 Earth pressure distribution curves along the up-slope side of pile shaft with dilation angle

4.3.3 桩前受力分析

图11为抗滑桩桩前土压力的分布。

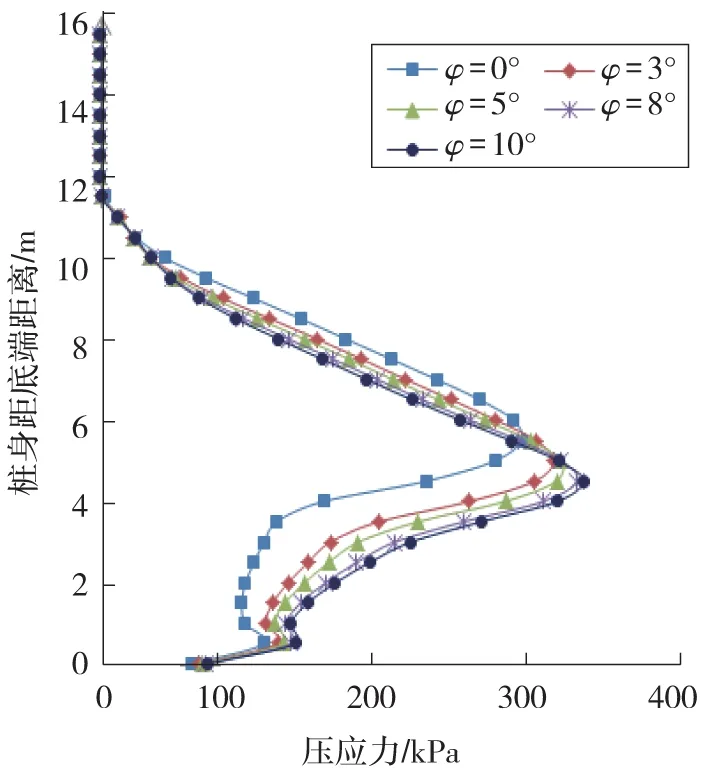
图11 剪胀角变化条件下桩前压力分布曲线Fig.11 Earth pressure distribution curves along the down-slope side of pile shaft front with dilation angle

从图11中可以更加清晰地看出滑动区的深度，此范围内桩前土体与桩身之间脱离，接触压力接近为0。在准嵌固段内，在桩身弯曲变形的挤压作用下，位置靠上的作用点受压程度大于靠下位置的作用点，并且受压影响大于自重应力的影响，使得准嵌固段内土压力随深度逐渐减小。在过渡段内，土体的松动作用大于桩身弯曲变形的影响，并随着深度的增加，过渡段内土体的松动作用逐渐减弱，因此沿桩身向下桩前土压力随深度增加而增加，且在接近准嵌固段顶时达到最大。在上层滑动段的影响下桩身发生变形，使得桩前一侧过渡段和准嵌固段土体受压，而桩前一侧过渡段和准嵌固段土体有卸载趋势，因此此段深度范围内，桩前一侧土压力要大于桩后一侧土压力。

由此可见，剪胀角对桩前土压力的分布与对桩后土压力沿桩身分布的影响是完全相反的。除此之外，从图11中还可知，剪胀角不同，作用在桩身的最大土压力的位置也有所不同，并与桩后不同。具体来说，剪胀角越大，作用在桩身最大被动土压力的位置距离桩底越近，当剪胀角φ=0°时，最大被动土压力为291 kPa；当剪胀角φ=10°时，最大被动土压力为334 kPa，增幅约14.8%。

综上所述，对于抗滑桩加固的边坡体系，土体剪胀角越小，边坡体系的安全系数越小，作用在桩身上的最大土压力也越小，导致抗滑桩的变形也越小。如果采取传统的观点(即将非零剪胀角近似取为0°)，对于边坡失稳的安全系数是保守的做法，但剪胀角φ=0°时，表现为土体更容易“流过”桩体，模拟得到的桩体受力要比真实受力要小。从抗滑桩设计角度来看，把非零剪胀角取为0°却是一种不安全的做法。

5 结 论

采用数值算例研究了剪胀角对土质边坡以及有抗滑桩加固的边坡体系的影响，得到如下结论：

1)对于剪胀角对边坡安全系数的影响，传统上有两种观点，即随剪胀角增大边坡的安全系数也相应增大的观点和随剪胀角增大安全系数呈现先增大后减小的抛物线样式的观点。通过采用有限元强度折减法和重力加载法对上述观点进行验证，结果发现采用有限元强度折减法对非关联塑性土质边坡的稳定性进行分析存在局限性，只有在折减的过程中满足剪胀角小于内摩擦角(即φr>φ)的条件，强度折减法才是有效的。

2)通过对有抗滑桩加固的边坡体系进行研究，沿桩身将桩身或坡体分为3个区段，即上层滑动段、中层过渡段和下层准嵌固段。发现抗滑桩桩身土压力随剪胀角的变化呈现“桩前大则桩后小，桩后小则桩前大”的特点。剪胀角越小，抗滑桩的变形越小，作用在桩身上的最大土压力也越小，表现出土体更加容易“流过”桩体的特点。

3)从边坡安全系数计算的角度考虑，把剪胀角近似取为0°可以得到最小的安全系数，是一种的偏于安全的做法。但是从抗滑桩设计的角度考虑，把剪胀角近似取为0°时，低估了桩身受力，又是一种偏于不安全的做法。表明实际边坡工程中应合理考虑剪胀角的取值，根据桩身的实际土压力分布来确定桩身弯矩以及桩身配筋。

[1] VERMEER P A.Non-AssociatedPlasticityforSoils,ConcreteandRock[M]. Delft, Netherland: Heron，1984：1-63.

[2] 张培文，陈祖煜.剪胀角对求解边坡稳定的安全系数的影响[J].岩土力学，2004，25(11)：1757-1760. ZHANG Peiwen, CHEN Zuyu. Finite element method for solving safety factor of slope stability[J].RockandSoilMechanics, 2004，25(11)：1757-1760.

[3] 蒋青青，陈占锋，赖伟明，等.考虑坡顶超载情况下的边坡剪胀效应分析[J].中南大学学报(自然科学版)，2009，40(2)：498-502. JIANG Qingqing, CHEN Zhanfeng, LAI Weiming, et al. Dilation effect of slope under over-loading on top of its surface[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2009，40(2)：498-502.

[4] LEE Fook-Hou, HONG Sze-Han, GU Qian, et al. Application of large three-dimensional finite-element analyses to practical problems[J].InternationalJournalofGeomechanics, 2011，11(6)：529-539.

[5] ZIENKIEWICZ O C, HUMPHESON C，LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Géotechnique，1975，25(4)：671-689.

[6] 陈曦，程勇刚.加速对称刚度矩阵技术及其在岩土有限元分析中的应用[J].岩土工程学报，2011，33(8)：1216-1221. CHEN Xi, CHENG Yonggang. Accelerated symmetric stiffness matrix technique and its applications in geotechnical finite element analysis[J].ChineseJournalofGeotechnicalEngineering, 2011，33(8)：1216-1221.

[7] 熊欢，肖盛燮.基于Drucker-Prager系列准则的边坡安全系数计算方法[J].重庆交通大学学报(自然科学版)，2010，29(4)：582-586. XIONG Huan, XIAO Shengxie. Calculation method of slope stability safety factor based on the Drucker-Prager criterion[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2010，29(4)：582-586.

[8] CHEN Xi, WU Yongkang, YU Yuzhen, et al. A two-grid search scheme for large-scale 3-D finite element analyses of slope stability[J].ComputersandGeotechnics, 2014，62：203-215.

[9] 陈寅春，胡文亮.基于有限元强度折减法多级边坡稳定性研究[J].重庆交通大学学报(自然科学版)，2014，33(6)：100-103. CHEN Yinchun, HU Wenliang. Stability study of multi-step slope based on strength reduction method[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2014，33(6)：100-103.

[10] DAWSON E M, ROTH W H, DRESCHER A. Slope stability analysis by strength reduction[J].Géotechnique，1999，49(6)，835-840.

[11] WON J, YOU K，JEONG S, et al. Coupled effects in stability analysis of pile-slope systems[J].ComputersandGeotechnics, 2005，32(4)：304-315.

[12] 孔位学，芮勇勤，董宝弟.岩土材料在非关联流动法则下剪胀角选取探讨[J].岩土力学，2009，30(11)：3278-3282. KONG Weixue, RUI Yongqin, DONG BAOdi. Determination of dilatancy angle for geomaterials under non-associated flow rule[J].RoilandSoilMechanics, 2009，30(11)：3278-3282.

[13] 康亚明，刘长武，贾延，等.剪胀性对边坡潜在滑动面的影响[J].中国矿业，2008，17(4)：89-94. KANG Yaming, LIU Changwu, JIA Yan, et al. The influence of the dilatancy character on the potential sliding surface of soil slopes[J].ChinaMiningMagzine, 2008，17(4)：89-94.

[14] 陈曦，刘春杰.有限元强度折减法中安全系数的搜索算法[J].岩土工程学报，2010，32(9)：1443-1447. CHEN Xi, LIU Chunjie. Search algorithms for safety factor in finite element shear strength reduction method[J].ChineseJournalofGeotechnicalEngineering, 2010，32(9)：1443-1447.

(责任编辑 刘 韬)

Stability Analysis and Evaluation of Soil Slope System Considering the Shear Dilatancy Effect

CHEN Xi1，ZHANG Xunwei1，2，MIAO Jianglong1，WANG Dongyong1

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044，P.R.China；2.China Overseas Engineering Group Co.Ltd.，Beijing 100048，P.R.China)

Based on numerical calculation examples the influence of soil expansion on earth side slope and the stability of side slope system was studied and two different views regarding dilatancy impact on slope stability were compared and these two different methods of finite element strength reduction and gravity loading method were tested and verified. The test results show that the finite element strength reduction method has its limit in stability analysis of side slope of non-associated platic earth nature and was only effective when statisfying the dilation angle less than internal friction angle in course of redcution. In addition, study was carried out regarding the view which stated that it is a safe method to take approximate dilation angle 0°. After study made on the side slope strengthened with anti-slide pile it was found that the less is the dilation angle, the less is the deflection of anti-slide pile and the maximum earth pressure acting on the pile shaft, which presented the characteristics that earth flow through pile body more easily. Hence considering from the respect of side slope safety factor, the minimum safety factor can be obtained by taking dilation angle approximately 0° , which is a safe practice. But considering from aspect of design of anti-slide pile this method is not safe. It is hence suggested that the value setting of dilation angle shall be reasonably considered by specific issue analysis according to specific conditions of slope.

geotechnical engineering; angle of dilation; slope system; anti-slide pile; factor of safety; strength reduction finite element method

10.3969/j.issn.1674-0696.2017.01.10

2015-10-16；

2015-11-22

中央高校基本科研业务费专项基金(2016JBM 043)

陈 曦(1977—)，男，辽宁辽中人，教授，博士，主要从事计算岩土力学方面的研究。E-mail: xichen.geo@gmail.com。

U416.1+4；O319.56

A

1674-0696(2017)01-052-06