带互异权值的渐进迭代逼近算法及其应用

张 莉，赵 林，檀结庆,2

(1.合肥工业大学 数学学院， 安徽 合肥 230009； 2.合肥工业大学 计算机与信息学院， 安徽 合肥 230009)

带互异权值的渐进迭代逼近算法及其应用

张 莉1，赵 林1，檀结庆1,2

(1.合肥工业大学 数学学院， 安徽 合肥 230009； 2.合肥工业大学 计算机与信息学院， 安徽 合肥 230009)

在计算机辅助几何设计(CAGD)领域,渐进迭代逼近(PIA)算法因其具有很好的自适应性和收敛稳定性，被广泛应用于插值与逼近问题.其中带权渐进迭代逼近(WPIA)算法通过调整向量加权明显加快了收敛速度.提出了一种带互异权值的渐进迭代逼近算法,不仅操作灵活,还可根据需要对各控制顶点进行调整，实现不同的迭代效果;同时通过引入一个参数,给出了可调权值迭代算法,当参数取合适值时，该算法的收敛速度比带权PIA算法更快,且权值取法不依赖于配置矩阵的特征值.最后用数值实例,通过对Bézier曲线、张量积Bézier曲面,以及三角Bézier曲面进行迭代,展示了该算法的有效性.

渐进迭代逼近；带权渐进迭代逼近；插值与逼近；Bézier曲线曲面；三角Bézier曲面

Progressive iterative approximation with different weights and its application. Journal of Zhejiang University(Science Edition), 2017,44(1):022-027

在计算机辅助几何设计与逆向工程中,构造一组不同精度的拟合曲线(曲面)进行插值或逼近于一个给定的有序点集是一类很重要的课题.为了更好地解决这一问题,早在1975年,齐东旭等[1]就提出了均匀三次B-spline曲线的盈亏修正算法;1979年DE BOOR[2]在报告中也阐述了类似的思想.

2004年,蔺宏伟等[3]用逐步迭代非均匀B-spline曲线曲面的方法拟合给定点集,证明了非均匀三次B-spline曲线(曲面)具有盈亏修正性质;2005年,蔺宏伟等[4]进一步证明了所有的标准全正基(NTP bases)混合曲线(曲面)都具有这一性质,并将此迭代方法命名为渐进迭代逼近(progressive iterative approximation, PIA).DELGADO等[5]发现规范B基在所有NTP基函数中收敛速度最快.2011年,陈杰等[6]给出了三角域上的PIA方法,证明了三角Bézier曲面和有理三角Bézier曲面在均匀参数化下的PIA性质.

为研究PIA方法与传统的代数插值方法之间的关系,邓少辉等[7]推导了代数插值和PIA方法之间的等价关系.蔺宏伟[8-9]给出了PIA方法的局部性质和收敛性证明,并将局部性质应用于自适应数据拟合技术中,取得了很好的迭代效果.

陆立正[10]通过对调整向量加权的方式对PIA方法进行加速(简称为WPIA),并给出了最优的权值取法.陈杰等[11]给出了WPIA方法的2种推广:带权的局部PIA方法和均匀参数化下的三角Bézier曲面的带权PIA方法.2015年,刘晓艳等[12]结合Jacobi迭代法,提出了非均匀三次B样条曲线插值的Jacobi-PIA算法,对PIA迭代进行加速.

2011年,蔺宏伟等[13]给出了逼近型PIA迭代格式,实现了PIA对大量数据的拟合.2014年,邓重阳等[14]提出了一种新的逼近型PIA方法,迭代的极限曲线或曲面是给定数据点的最小二乘拟合.基于诸多学者对PIA的大量研究与应用,蔺宏伟[15]从理论和应用两方面对PIA方法进行了综述,展示了PIA方法在多个领域成功应用的实例.

本文提出一种带互异权值的PIA方法,在迭代过程中,每一个控制顶点所对应的调整向量都乘以不同的权值,增加了实际操作的灵活性.当基函数是三次非均匀B样条基、权值取某些特殊值时,文献[12]中的方法即为本文方法的特例;当所有权值都相等时,本文方法就是WPIA方法,数值实例表明，当取一组合适的权值时,本文方法比WPIA方法收敛速度更快;此外,还给出一种权值的取法，在减少计算量的同时(不需要求矩阵特征值),收敛速度更快.

1 参数曲线带互异权值的PIA方法

1.1 迭代格式的导出

是一个全正矩阵.

类似地,第k+1步的迭代为

为加速收敛的同时增加操作的灵活性,对上述迭代步骤做如下调整：

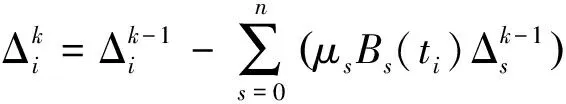
Δk=(I-BW)Δk-1=(I-BW)kΔ0,

(1)

其中,I是n+1阶单位矩阵,

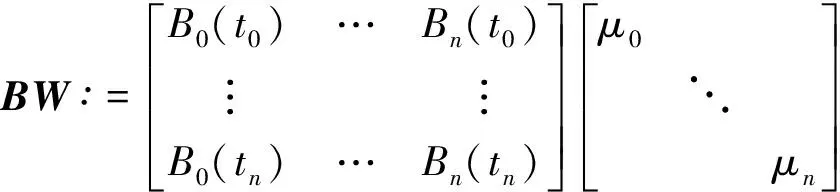
B为基函数{Bi(t)}在参数{ti}(i=0,1,…,n)下的配置矩阵,W=diag(μ0,μ1,…,μn)称为权矩阵.

1.2 迭代格式(1)的收敛性

定理1 迭代格式(1)是收敛的,即迭代的极限曲线插值于给定的数据点.

证明 由基函数的非负性及归一化性质可得

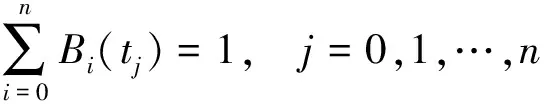
0<λi(BW)<2,

所以迭代矩阵D=I-BW的特征值满足

-1<λi(D)=1-λi(BW)<1,

D的谱半径ρ(D)<1,则迭代格式(1)收敛.那么

即极限曲线插值于初始数据点.

定理2 当迭代格式(1)的权值取

时，其中a∈(0,2),迭代格式(1)亦收敛.

证明 矩阵BW的列范数

矩阵BW的特征值满足

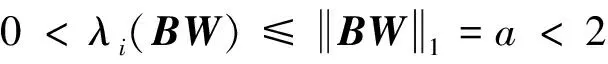
-1<λi(D)=1-λi(BW)<1,

所以ρ(D)<1，迭代格式(1)收敛.

2 张量积曲面PIA方法的改进

2.1 迭代格式的导出

设第k+1次迭代的曲面为

其中，

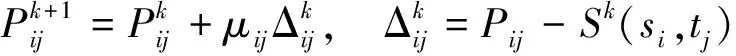
由此得到如下迭代格式：

Δk=DΔk-1=DkΔ0,

(2)

其中，

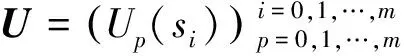
2.2 迭代格式(2)的收敛性

类似于曲线的情况,对于张量积曲面,同样给出了关于收敛性分析的2个定理.并且定理的证明与曲线的情况类似，注意矩阵B为2个配置矩阵的Kronecker积即可.

定理3 迭代格式(2)是收敛的,即极限曲面插值于给定的数据点.

定理4 当迭代格式(2)中的权值取

时(p=0,1,…,m,q=0,1,…,n),迭代格式(2)收敛.

3 三角Bézier曲面PIA方法的改进

3.1 迭代格式的导出

三角域T∶={(u,v,w)∶u,v,w≥0,u+v+w=1}上的一个n阶三角Bézier曲面为

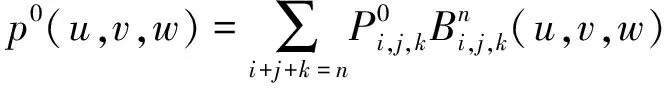
随着迭代的进行,可得到第l+1次的曲面为

为便于表达,引入字典顺序的定义.

定义[16]给定2个d维向量α,β,若α-β=(α1-β1,α2-β2,…,αd-βd)的第1个非零元为正数，则向量α排在向量β之前,记作α>β.那么,定义在三角域T上的n阶三角Bernstein基函数,可表示为(n+1)(n+2)/2维的行向量

参数序列为

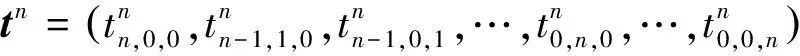
则得到如下迭代格式

Δl+1=(I-BW)Δl=(I-BW)l+1Δ0，

(3)

3.2 迭代格式(3)的收敛性

定理5 迭代格式(3)是收敛的,即极限曲面插值于给定的数据点.

证明 双变量Bernstein基函数Bn在参数tn下的配置矩阵为

由于双变量Bernstein基函数的非负性和归一性，

则矩阵B的无穷范数为

所以矩阵B的特征值λi,j,k(B)满足

0<λi,j,k(B)≤1, i+j+k=n.

又由于μi,j,k∈(0,2),那么矩阵W的特征值和无穷范数满足

0<λi,j,k(W)=μi,j,k<2，

0<λi,j,k(BW)<2,

-1<λi,j,k(D)=1-λi,j,k(BW)<1,

矩阵D的谱半径ρ(D)<1,则迭代格式(3)收敛.即

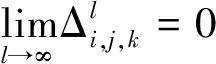
那么，极限曲线插值于初始数据点.

定理6 当迭代格式(3)中的权值取

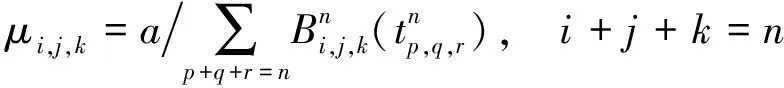
证明 矩阵BW的列范数为

此时,矩阵BW和D的特征值分别满足

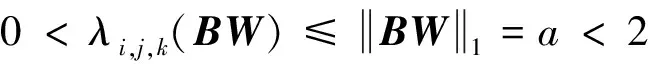
-1<λi,j,k(D)=1-λi,j,k(BW)<1,

所以ρ(D)<1,迭代格式(3)收敛.

4 数值实例

用Bézier曲线、张量积Bézier曲面,以及三角Bézier曲面进行迭代,逐步插值于给定数据点,并将本文方法与经典PIA[4]和取最佳权值的WPIA方法[10-11]进行比较.

数值实例均采用均匀参数化方法;曲线，张量积曲面和三角曲面第k步迭代的误差分别取

例1 在圆弧p(t)=(sin t,cos t)上取样本p(ti)(ti=πi/6,i=0,1,…,10)作为数据点，并作Bézier曲线.图1中黑色的是使用本文方法取a=1.4迭代后的曲线.表1展示了圆弧在相同迭代次数下不同PIA方法的误差比较.

图1 使用本文方法迭代例1中的数据点Fig.1 Iterate the data in example 1 using our method

所用方法迭代次数03510PIA方法0．29300．02140．00840．0023WPIA方法0．29300．07850．05060．0176本文方法0．29300．01370．00420．0009

由表1知,在相同迭代次数下,本文方法的误差明显较小.需要注意的是,WPIA算法的加速收敛作用会随着迭代次数的增加而渐趋明显,而在迭代之初,其加速作用不明显.

例2 图2展示的是以类peaks曲面上的点(1,1,1),(1,2,4),(1,3,2),(1,4,2),(1,5,2),(2,1,2),(2,2,2),(2,3,3),(2,4,6),(2,5,4),(3,1,3),(3,2,2),(3,3,4),(3,4,4),(3,5,3),(4,1,4),(4,2,6),(4,3,1),(4,4,1),(4,5,2)为数据点,取a=1.9,采用本文方法迭代后的张量积Bézier曲面.表2列出了各方法的误差.

表2 例2中相同迭代次数下不同方法的误差比较

例3 图3展示的是以字典顺序排列的点列{(0,3,0.3),(-0.5,2,3),(0.5,2,4),(-1,1.5,1),(0,1.4,3),(1,1.5,0.5)}为数据点,取a=1.2，使用本文方法迭代后的三角Bézier曲面.表3列出了相应的误差,可以看出迭代效果有显著改善.

图2 使用本文方法迭代类例2中的数据点Fig. 2 Iterate the data in example 2 using our method

图3 使用本文方法迭代例3中的6个数据点Fig. 3 Iterate the data in example 3 using our method

所用方法迭代次数0159PIA方法1．80430．90220．05640．0035WPIA方法1．80430．60140．00749．2×10-5本文方法1．80430．36095．8×10-49．2×10-7

5 结 论

给出了一种带互异权值的PIA方法.在调整过程中，对不同的数据点分配不同的权值,操作较灵活；同时给出了一组含参数的权值,在迭代次数不变的情况下通过调控参数可以得到更小的误差；并且本文方法不必依赖于矩阵特征值;此外，WPIA的加速收敛作用在迭代之初不明显，需多次迭代才显现，而本文方法在迭代前期误差就很小.

数值实验证明,本文方法不仅适用于Bézier曲线和张量积Bézier曲面,亦适用于三角Bézier曲面.

[1] 齐东旭,田自贤,张玉心，等.曲线拟合的数值磨光方法[J].数学学报,1975,18(3):173-184. QI D X, TIAN Z X, ZHANG Y X, et al. The method of numeric polish in curve fitting [J]. Acta Mathematica Sinica,1975,18(3):173-184.

[2] DE BOOR C. How does Agee’s smoothing method work[J/OL]. [2016-7-10]. http://ftp.cs.wisc.edu/debooron/ agee.pdf.

[3] 蔺宏伟,王国瑾,董辰世.用迭代非均匀B-spline曲线(曲面)拟合给定点集[J].中国科学:E辑,2004,33:315-331. LIN H W, WANG G J, DONG C S. Constructing iterative non-uniform B-spline curve and surface to fit data points [J]. Science in China: Ser E,2004,33:315-331.

[4] LIN H W, BAO H J, WANG G J. Totally positive bases and progressive iteration approximation [J]. Computers and Mathematics with Applications,2005,50(3/4):575-586.

[5] DELGADO J, PENA J M. Progressive iterative approximation and bases with the fastest convergence rates [J]. Computer Aided Geometric Design,2007,24(1):10-18.

[6] CHEN J, WANG G J. Progressive iterative approximation for triangular Bézier surfaces [J]. Computer-Aided Design,2011,43(8):889-895.

[7] 邓少辉,汪国昭.渐进迭代逼近方法的数值分析[J].计算机辅助设计与图形学学报,2012,24(7):879-884. DENG S H, WANG G Z. Numerical analysis of the progressive iterative approximation method [J]. Journal of Computer-Aided Design and Graphics,2012,24(7):879-884.

[8] LIN H W. Local progressive-iterative approxim-ation format for blending curves and patches [J]. Computer Aided Geometric Design,2010，27(4):322-339.

[9] LIN H W. Adaptive fitting by the progressive-iterative approximation [J]. Computer Aided Geometric Design,2012,29(7):463-473.

[10] LU L Z. Weighted progressive iteration approximation and convergence analysis[J]. Computer Aided Geometric Design,2010,27:129-137.

[11] 陈杰,王国瑾,金聪健.两类推广的渐近迭代逼近[J].自动化学报,2012,38(1):135-139. CHEN J, WANG G J, JIN C J. Two kinds of generalized progressive iterative approximations [J]. Acta Automatica Sinica,2012,38(1):135-139.

[12] 刘晓艳,邓重阳.非均匀三次B样条曲线插值的Jacobi-PIA算法[J].计算机辅助设计与图形学学报,2015,27(3):484-491. LIU X Y, DENG C Y. Jacobi-PIA algorithm for non-uniform cubic B-spline curve interpola-tion[J]. Journal of Computer-Aided Design& Graphics,2015,27(3):484-491.

[13] LIN H W, ZHANG Z Y. An extended iterative format for the progressive-iteration approximation [J]. Computers & Graphics,2011,35:967-975.

[14] DENG C Y, LIN H W. Progressive and iterative approximation for least squares B-spline curve and surface fitting[J]. Computer-Aided Design,2014,47(1):32-44.

[15] 蔺宏伟.几何迭代法及其应用综述[J].计算机辅助设计与图形学学报,2015,27(4):582-589. LIN H W. Survey on geometric iterative methods with applications[J]. Journal of Computer-Aided Design& Graphics,2015,27(4):582-589.

[16] DUNLL C, XU Y. Orthogonal Polynomials of Several Variables[M]. Cambridge: Cambridge University Press,2001.

ZHANG Li1, ZHAO Lin1, TAN Jieqing1,2

(1.SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China; 2.SchoolofComputerandInformation,HefeiUniversityofTechnology,Hefei230009,China)

In CAGD, progressive iterative approximation (PIA) method is widely used to solve interpolation and approximation problems due to its perfect adaptability and convergence stability. Weighted progressive iterative approximation (WPIA) can accelerate the convergence rate by assigning an appropriate weight for each adjusting vectors. One new PIA method with mutually different weights is presented. It not only provides more flexibility in operation, but also achieves satisfactory iterative result for different control vertices. A set of weights with an adjustable parameter has also been put forward, which can be obtained without resorting to the eigenvalue of collocation matrices and can speed up the convergence rate compared with the WPIA method. Numerical examples of Bézier curves, tensor-product Bézier surfaces and triangular Bézier surfaces demonstrate the effectiveness of the method.

progressive iterative approximation(PIA); weighted progressive iterative approximation (WPIA); interpolation and approximation; Bézier curves and surfaces; triangular Bézier surfaces

2016-07-15.

国家自然科学基金重点资助项目(U1135003);国家自然科学基金资助项目(61472466,61100126);中国博士后科学基金面上资助项目(2015M571926);浙江大学CAGD&CG国家重点实验室开放课题(A1607).

张 莉(1976-),ORCID:http://orcid.org/0000-0002-9208-1949，女，博士，教授，主要从事CAGD研究，E-mail：lizhang@hfut.edu.cn.

10.3785/j.issn.1008-9497.2017.01.003

TP 391.41

A

1008-9497(2017)01-022-06