高中数形结合解题技巧的总结与分享
李梦晗
(山东省济宁市鱼台县第一中学高二(12)班 272300)
所谓数形结合思想,即高中阶段数学解题期间,利用图形和方程式的结合,以简化数学习题的一种方法.这种解题方法能够实现数字与图形的相互分析,将其转化为相对较为简便的数量关系.
一、数形结合概述
数形结合简而言之就是通过分析数学问题本身所蕴含的内在层次和结构,梳理其中的已知条件、结论的联系,这种分析除了具有代数含义以外,也体现了几何含义.通过数学问题中各种关系的结合,将其与空间形式进行融合,在此基础上确定解决问题的思路与方法,使数学问题得以有效解决.其本质是使抽象性的数学语言与直观性的图形进行充分的融合,尤其是代数与形象图表的结合,可以使代数问题呈现出几何化的特点,使抽象问题更加形象化.
其实在高中数学中,数形结合思想的应用非常普遍,例如求解函数相关问题时,便可以建立函数模型,通过函数图像的方式求解最终的参数取值范围.其实也可以在求解的过程中对方程根的范围进行求解,并且求出各数值的关系.不仅如此,数形结合也能够使代数问题更加几何化,通过几何模型的方式对问题本质进行分析,以此解决数学问题.其实也能够对几何习题中的斜率、截距进行求解,进而获得最大值与最小值.最后,数形结合也可以用在图形形状与位置关系等的研究和求解上,对图形存在的内在联系进行分析,并且求解出最终的结论.
二、高中数形结合解题技巧的总结与分享
1.以数转形
因为数学图形具有直观、形象的特点,相较于数学语言存在非常大的优势,所以,高中数学知识也可以将一些抽象且求解比较难的代数问题,通过数形结合的形式转变为图形问题, 以此顺利地梳理出我们的解题思路.了解有效的解题方式,完成解题,从而提升我们的数学解题水平.
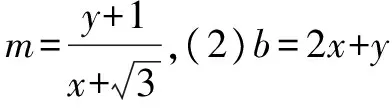
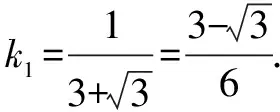
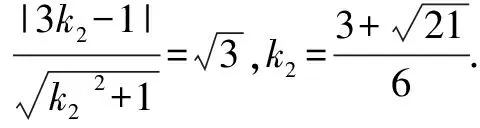
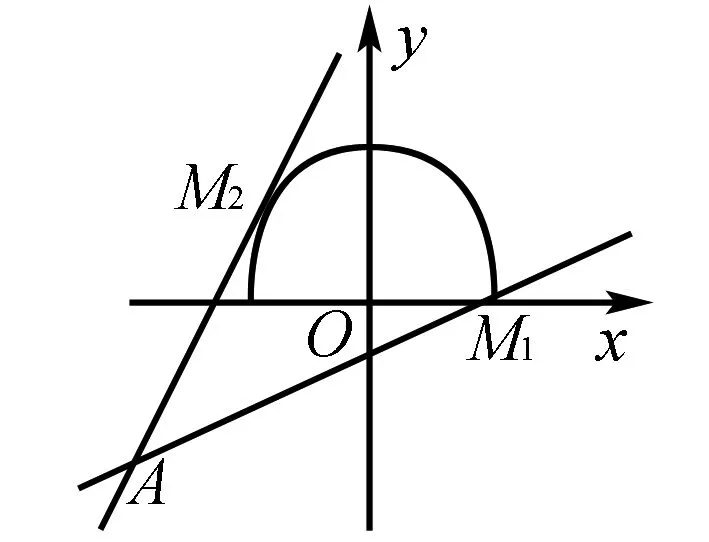
图1
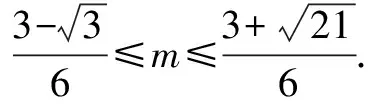
(2)将b视为斜率为-2,过半圆x2+y2=3(y≥0)上的点P(x,y)的直线在y轴上的截距.由图可知,n1≤b≤n2(n1、n2分别代表直线BP1、CP2的截距).
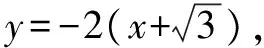
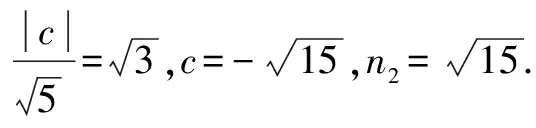
通过例1可知,对于一些不等式问题的求解,为了能够更加全面、快速地求解出正确答案,我们可以运用以数转形这一方法进行求解.如此一来,不仅拓展了我们的解题思路,提高解题速度,同时也通过直观的图形的提高观察能力,为思维的发散奠定基础.
2.以形转数
虽然图形具有直观、形象等多种优势,但是也存在一些不足,例如计算过程的准确性与推理的逻辑性.特别是一些数学问题方面,这种逻辑性和准确性就更加明显.所以,对于这些问题,就不能只是运用图形进行求解,以免出现错误.基于此种情况,可以通过数形结合的方式,将图形转变为代数语言的形式,通过另一种途径对数学问题进行求解.
例2 设函数y=f(x)是最小正周期为2的偶函数,在区间[0,1]上的图象为如图2所示的线段AB,则在区间[1,2]上,f(x)=____.
解析通过题目中已经给出f(x)在区间[0,1]的图象,所以可以使用图形结合和对称变形的方式进行求解.由于y=f(x)为偶函数,由“形”对称变换到“形”,得到函数y=f(x)在区间[-1,0]上的图象,如下图线段CA.由于y=f(x)是最小正周期是2的函数,再由“形”向右平移至“形”,最终获得函数y=f(x)在区间[1,2]上的图象,如下图所示线段BD.f(x)=x,x∈[1,2].
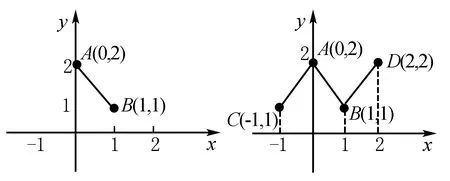
图2 图3
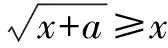
A.1 B.2 C.3 D.4
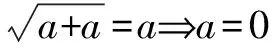
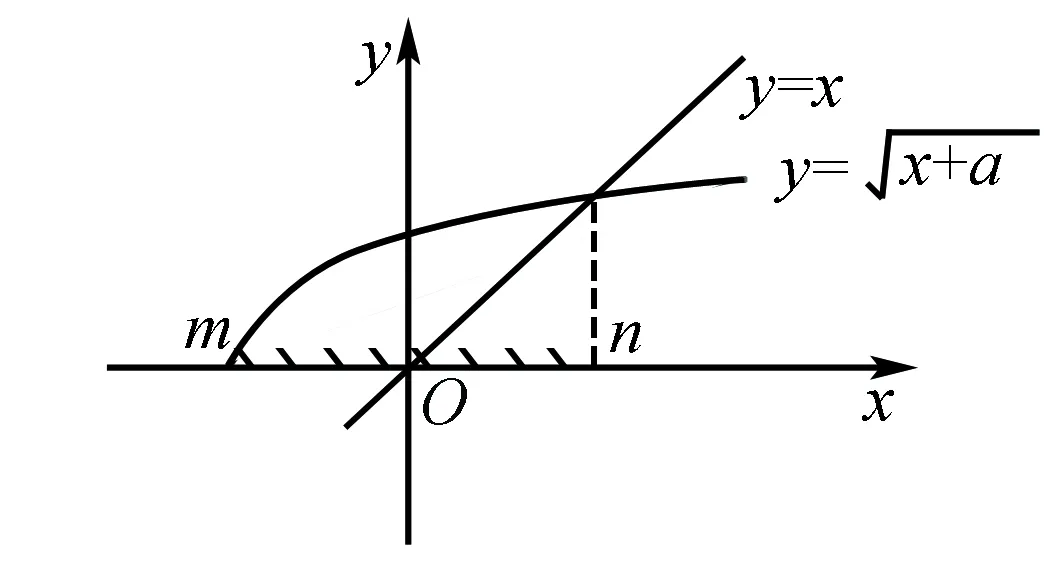
图4
此题特别好地体现了数形结合的作用,若只是以数的角度出发解题,可以得到m=-a和n=a,但是这一求解存在很大的难度.然而若是以形的角度出发进行解题,便可以非常直接地求出最终答案.这也就说明了当求解小题时必须要对这一思想进行重视.
由此可见,一些数学问题中求取具体值不能使用图形进行准确求值,因此,将图形转变为代数问题,可以使我们快速求解问题并且获得最终答案.在这一环节当中,作为学生,需要全面考虑,综合考虑题目中已知条件和所有可能性,只有这样才能获得准确的答案.
[1]江士彦. 浅析高中数学数形结合的解题技巧[J]. 读与写(教育教学刊),2015,12(10):89.
[2]麦康玲. 数学分析思想在高中数学解题中的应用[J]. 科教文汇(下旬刊),2015(05):110-111.
[3]王华. 高中数学应用题解题教学策略及学生学习技巧研究[J]. 科技信息,2014(11):192+232.

