浅谈如何在习题评讲中培养学生的数学核心素养

——对一道圆锥曲线题的再思考

谢 丽

(江苏省镇江市丹徒高级中学 212000)

一、案例分析

例 已知圆O:x2+y2=4,点Q是直线x=4上一个动点，过点Q向圆O作切线，切点分别为A,B.

(1)证明：直线AB经过定点P，并求出定点P的坐标；

(2)在(1)中，设直线AQ,PQ,BQ的斜率分别为k1,k2,k3.

证明：k1-2k2+k3为定值.

1.概念本质不清，思维方向不明：无的放矢

分析 第(1)题的考点是求直线所过定点问题，直线方程如何表示，假设哪个参数，目标是什么？如何确立思路？通过一系列有针对性的问题，帮助学生自行找出思维的突破口，即用某个参数表示出直线的方程，然后再研究所过定点.

解析过程 (1)连接AC,BC则A,C,B,Q四点共圆，此圆设为圆M,QC为此圆M的直径,AB为圆M与圆C的公共弦，设Q(4,t),则圆M的方程为x(x-4)+y(y-t)=0即x2+y2-4x-ty=0①.

又圆C的方程为x2+y2=4 ②.

将①减去②，即有公共弦AB所在的直线方程为 4x+ty=0.从而有动弦AB所在的直线经过定点P，且定点P的坐标为(1,0).

2.抽象思维能力缺乏，数学意识淡薄：踌躇不前

对于第(2)问学生选择了很多不同的解答方法，但是大部分都由于计算量太大而放弃了.数学问题较抽象，数学教与学逐步从具体到抽象，从“混而不错”中找到问题解决不了的关键因素，“追根溯源”，从而找到突破口.在教与学的过程中不断提高学生的数学计算能力.比如(2)的解题过程中：

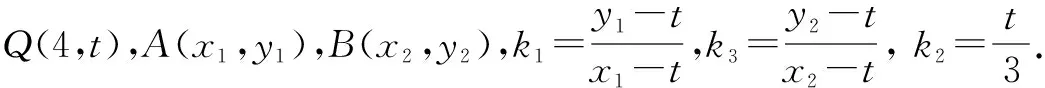
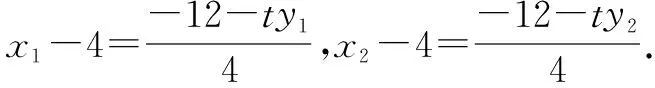
以上这些步骤很多学生都是可以达成的，如下的计算就有些力不从心了：

下面的计算就很有玄机：目标是要得到k1=2k2+k3为定值其中k1,k2,k3的表达形式一致，那么如果继续通分加以化简，就会遇到较大的计算量:

这个计算量是相当大的，这种做法最终也因式子的繁杂无法继续而放弃了.那那如何找到简化计算的突破口呢?

在教学过程中这一步其实可以继续探究一下，结论是要得到k1-2k2+k3为定值，也就是最终的结果参数都是可以抵消的.观察一下系数,k1+k3和-2k2,系数之和为0，这样，教师就可以给学生以新的提示：

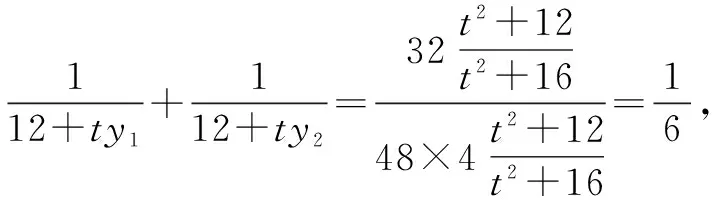
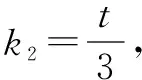
这种简化计算的方法，是在学生已有的过程中找出突破口，让问题的解决得到转机.

3.思维理性不足，心理活动定式:一意孤行

在笔者备课的过程中，时常会去考虑学生已有的知识储备以及该题与课本习题之间问题的关联，不难发现，本题我们可以有更为值得探讨和可以普及的方法：

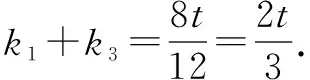
故k1-2k2+k3为定值结论成立.

这种解法恰巧只用到最最基本的直线与圆的位置关系中相切的几何意义，数形结合.通过不断观察，找到合适的数学模型.理性思维是学生的核心思维能力，也是组成个人数学核心素养的关键因素.

二、教学思考

以上例题主要反映了学生审题能力不过关，概念理解不到位，建模过程不通畅，逻辑思维不明确，思维变通不灵活等问题，归根结底是教师没能真正理解教材意图，导致学生核心素养的培养任重而道远.

目前，高中数学教学普遍存在快节奏、大容量、教师讲得多、学生理解得少等现象.教师不自觉地把学生当作知识的容器，完成自己教学进度的工具.教学就要教思考，教体验、教表达.无论是思辨、发现、探究、体验、悟错，都不可能一蹴而就，需要我们有足够的时间去留给学生，让他们有机会去反思自我，展现自我，消化累积，在教与学的过程中静待花开！

[1]颜勇.数学核心素养的培养——从自主探究的维度思考[J].中国农村教育,2016(12):56-57.

[2]张彩艳.数学学科核心素养探析:内涵、价值及培养路径[J]. 教育导刊，2017(1)：60-74.