初中数学解决直角三角形问题常见的几种途径

任龙华

(江苏省海安县大公初中 226600)

初中数学教材中有不少关于直角三角形的相关知识，如直角三角形的两个锐角互余、直角三角形斜边上的中线等于斜边的一半、勾股定理和逆定理、利用三角函数解直角三角形、圆周角的推论和直角三角形全等或者相似的判定等等.其中，解决直角三角形问题常见的途径有勾股定理、直线解析式法和构造相似三角形等.下面就一些就有关直角三角形的一些常见题型加以解析说明，与同行们进行探讨．

一、运用勾股定理解决相关直角三角形问题

问题1 在Rt△ABC中，AC=3,BC=4,当AB等于多少时，△ABC为直角三角形．

点评本题主要考查了初中数学中的勾股定理知识和分类讨论的数学思想．勾股定理可以解决直角三角形的一些边长问题，在现实生活和数学中有着广泛的应用．同时，此题要引导学生仔细审题，弄清楚题意，要分情况加以讨论，防止学生遗漏，只考虑一种情况．

二、运用直线解析式法解决有关直角三角形问题

人教版八年级数学上册第十四章《正比例函数》中，通过直线平移，对其解析式的变化规律，我们可以得出结论：当直线互相平行时，它们的解析式中的k相等；再进一步的观察发现，当两条直线互相垂直时，它们解析式中的k互为负倒数，即k1·k2=-1．利用此规律，我们就可以解决一些有关的直角三角形或者垂直的相关问题．

解析我们注意到本题中，直线CD⊥AB，如果它们的直线解析式中的k分别为：k1、k2，我们利用规律则有k1·k2=-1，从而求出k2=-2．进而，我们设直线CD的解析式为y=-2x+b，再将点C(0,-1)代入，求出b=-1，所以直线CD为y=-2x-1．

点评虽然利用直线解析式k1·k2=-1的结论解决一些直线互相垂直问题或者直角三角形的问题对于初中生不作一般的要求，到了高中的平面解析几何中就比较常见．但此结论在人教版教材的书后习题中出现了，教者一般都作了补充说明，学生根据此结论解决相关的题型就会显得很简便．

三、通过构造相似三角形解决相关直角三角形问题

盘点各省市近几年的中考题，通过构造相似三角形解决等腰三角形或者直角三角形的问题经常会不断涌现，常见于求直角三角形未知点的坐标等．

问题3 在平面直角坐标系中，已知点A(0,1),B(5,6)，在x轴上找一点C，使△ABC是以AB为斜边的直角三角形，则C点坐标为多少？

点评通过作辅助线，我们要善于在题目中发现和构造基本图形，利用全等三角形或者相似三角形解决问题．从“三垂直型”到“三角相等型”，我们会发现很多直角三角形题目中都具有“三角相等型”，这类题目显而易见，选择构造相似三角形解题来得方便．本题中以AB中点为圆心，AB为直径作圆，如果与x轴有交点，那就是C点．

当然，对于上面的问题3，解法并不唯一，除了利用构造相似三角形来解决以外，我们也可以利用勾股定理、直线解析式或者根据中点公式再结合直角三角形斜边上的中线等于斜边的一半等知识来解决．

在解决直角三角形相关的综合问题时，有时这三种不同的方法都可以运用，学生可以根据具体情况选择一种比较简便的方法来解题或者将这三种方法中的某两种结合起来使用，使得解题过程更简便．

问题4 在平面直角坐标系中，抛物线y=ax2+bx+3与x轴的两个交点分别为A(-3,0),B(1,0)，过顶点C作CH⊥x轴于点H．

(1)直接填写：a=____,b=____,顶点C的坐标为____；

(2)在y轴上是否存在点D,使得△ACD为直角三角形？若存在，求出点D的坐标；若不存在，说明理由；

解析第(1)问中，直接将A、B两点的坐标代入，得到关于a、b的方程组，求出a=-1，b=-2，从而得出抛物线的解析式．再根据抛物线的轴对称性，把x=-1代入解析式，得到y=4，所以顶点为C(-1,4)．第(2)问，由于题目没有指明△ACD中哪个角是直角，所以要分三种情况进行讨论，而同时这三种途径都可以用来解决本题中的直角三角形问题．

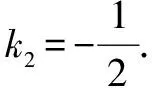
最后，方法三：我们还可以构造相似三角形来解题．分三种情况：

当然，学生可以从中选择其中一种的方法解题，或者当C点、A点为直角顶点时，学生可以选择直线解析式法比较简便，当D点为直角顶点时，选择构造相似三角形解题比较简便，也就是将其中两种方法结合起来解题，这样比较快捷灵活、简便易懂．

总而言之，对于数学学习，要进行整理和归纳总结，把知识的点、线、面结合起来交织成知识网络，纳入自己的知识体系，以此引领学生的真正掌握.

[1]刘辉.初中数学例题教学现状研究[D]. 武汉：华中师范大学 ,2013.