浅谈数学新定义题的解题策略——以2017年中考试题为例

陆炜锋

(江苏省海门市六甲初级中学 226100)

笔者对2017年各省市的新定义题进行了深入细致的研究，感触很深．本文将对最具有代表性的题型特点进行分析，希望能对广大师生有一点点的帮助．

一、数与代数类试题

例1 (2017湖南益阳)在平面直角坐标系中，将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”，如(-3，5)与(5，-3)是一对“互换点”．

(1)任意一对“互换点”能否都在一个反比例函数的图象上？为什么？

(2)M、N是一对“互换点”，若点M的坐标为(m，n)，求直线MN的表达式(用含m、n的代数式表示)；

简解(1)不一定，理由略．

(2)由M(m，n)得N(n，m)，设直线MN的表达式为y=cx+d．

代入得解析式：y=-x+m+n；

∴ “互换点”是(2，-1)和(-1，2)，代入y=x2+bx+c，

∴此抛物线的表达式为y=x2-2x-1．

二、图形与几何类试题

例2 (2017黑龙江齐齐哈尔)经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”．如图，线段CD是△ABC的“和谐分割线”，△ACD为等腰三角形，△CBD和△ABC相似，∠A=46°，则∠ACB的度数为____．

简解AC≠CD．

②当DA=CD时，∠ACD=∠A=46°，∴∠ACB=46°+46°=92°.

评析本题可以将“线”的问题转化为“等腰三角形”和“相似三角形”的问题，而三角形的问题又都转化为“角”的问题．这样的“套路”是学生应该掌握的解题思路，它不是“题型+技巧”，而是一种“自然”的解法．需要注意的是，等腰三角形分类讨论的三种情况，可以去掉一种，这是灵活运用分类讨论思想、节省解题时间的表现．

三、统计与概率类试题

例3 (2017山东日照)若n是一个两位正整数，且n的个位数字大于十位数字，则称n为“两位递增数”(如13，35，56等)．在某次数学趣味活动中，每位参加者需从由数字1，2，3，4，5，6构成的所有的“两位递增数”中随机抽取1个数，且只能抽取一次．

(1)写出所有个位数字是5的“两位递增数”；

(2)请用列表法或树状图，求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率．

简解(1)15,25,35,45.

(2)树状图：

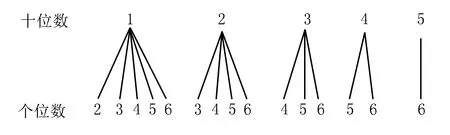
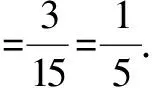
评析第(1)小题重在理解递增的含义；第(2)小题可以通过画树形图来表示，而树形图要省略不合题意的情况．此题的解题策略是品悟两位递减数的含义，引导学生回到定义中去(波利亚语)，找出与平时解题不同之处.

通过分析，我们发现：解新定义题，就是要细读定义关键词，理解本质特征，适时转化为“熟悉”问题.总之，解决此类问题，取决于已有知识、技能、数学思想的掌握和基本活动经验的积累，还需要不断的实践和反思，不然就谈不上“自然”的、完整的解题.

[1]戴向阳．浅谈中考“新知阅读理解”的解题策略[J]．中国数学教育(初中版)，2016 (11)：52-55，60．