惯导辅助下的动态精密单点定位算法研究

韩舒文,李峰,刘峰

(北京自动化控制设备研究所,北京100074)

0 引 言

精密单点定位( PPP)技术利用高精度的卫星星历和卫星钟差,仅靠单台接收机所采集到的双频伪距和载波相位观测量即可实现精密定位,长时间观测量收敛后可达到静态厘米级、动态分米级的定位精度。由于其定位方式简单,并且可以得到高精度的定位结果,因此,它在高精度的工程测量和动态的导航定位中都具有广阔的应用前景[1]。

惯性导航系统(INS)的运行具有很强的自主性,而利用全球定位系统(GPS)的卫星导航接收机在定位时需要持续接收来自至少四颗卫星的卫星信号才能实现定位。在真实的测量环境中,GPS电磁波信号的传播很容易受到障碍物的遮挡或是来自外界的干扰,从而导致信号中断或削弱,并引起接收机定位精度的降低甚至无法定位。在这种情况下,具有强抗干扰能力的INS仍然能够持续提供定位结果,保证定位有效[2]。此外,INS辅助GPS还在定位初始阶段整周模糊度的解算方面具有一定的优势,使整周模糊度能够更加快速、准确地求解。目前,许多学者充分利用了组合导航输出和惯性导航系统在对准阶段后的短时间内高精度的特点[3], 使得INS辅助信息可有效应用于辅助差分定位中整周模糊度的求解。文献[4]中采用了INS的航向角信息和位置信息辅助求解整周模糊度,并通过实验分析了惯导位置精度对模糊度搜索的影响。文献[5]同样利用了INS位置信息,在松组合和紧组合两种INS/GPS组合模式下分析了辅助方法对模糊度解算的积极作用。但在目前的文献中,将INS位置信息辅助用于精密单点定位方式中的研究较少。

本文详细给出了精密单点定位中采用最小二乘法进行参数估计的定位解算方法,并在此基础上加入惯性信息进行辅助,根据文献[4]、文献[5]中的紧组合模式,以及文献[5]中的松组合模式给出了位置代入法、虚拟观测量法这两种惯性辅助改进算法。最后,通过建立动态仿真场景,并将该场景下的伪距和载波相位观测量进行定位解算,验证了在惯性信息的辅助下可有效减小模糊度误差、缩短收敛时间,且两种改进算法最终的动态定位精度都较未辅助时有明显改善。

联系人: 韩舒文 E-mail:hanshuwen93@163.com

1 精密单点定位技术基本原理

1.1 PPP函数模型

目前,精密单点定位中主要有非组合模型、常规模型、UofC模型和无模糊度模型这四种函数模型。本文采用常规模型,利用双频伪距和载波相位观测值组成的无电离层组合作为定位的函数模型,其表达式为[6]

=ρ+c(δtr-δts)+T+δm+εPIF，

(1)

=ρ+c(δtr-δts)+T+λIFNIF+

δm+εΦIF，

(2)

式中：fi为双频中的第i个频率值；Pi和Φi分别为接收机r到卫星s之间第i个频率上的伪距和载波相位观测值；PIF和ΦIF分别为伪距和载波相位的无电离层组合观测值；ρ为卫星和接收机之间的真实几何距离；c为光速；δtr和δts分别为接收机钟差和卫星钟差；T为信号路径方向上的对流层延迟；δm为多路径延迟；εPIF和εΦIF分别为两种组合观测值的观测噪声及未被模型化的误差。式(2)中还存在组合观测值的波长λIF和组合观测值的整周模糊度NIF,其表达式分别为[7]

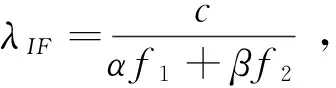
(3)

NIF=αN1+βN2，

(4)

式中,α和β为组合系数。对无电离层组合,有α=f1,β=-f2.

通过式(1)、(2)给出的常规模型可以消除一阶电离层所带来的影响,但同时也使得模糊度参数只能作为实数参数进行估计,模糊度不再具有整数特性。且观测噪声相对于原始观测量中存在的噪声有所放大,使得位置误差增大、趋于收敛的时间变长。

1.2 最小二乘估计模型

最小二乘法是在求解模糊度浮点解、进行参数估计时的常用方法。解算前,需要对如式(1)、(2)的非线性方程进行线性化处理,线性化后卫星s的伪距和载波相位无电离层组合观测方程可写为

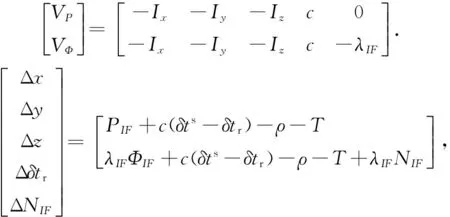
(5)

式中: -Ix、-Iy、-Iz分别为由卫星到接收机之间的几何距离得到的接收机位置坐标在三个方向上的偏导数； Δx、Δy、Δz分别为接收机坐标在三个方向上的改正量； Δδtr为接收机钟差改正量； ΔNIF为卫星s的模糊度改正量。

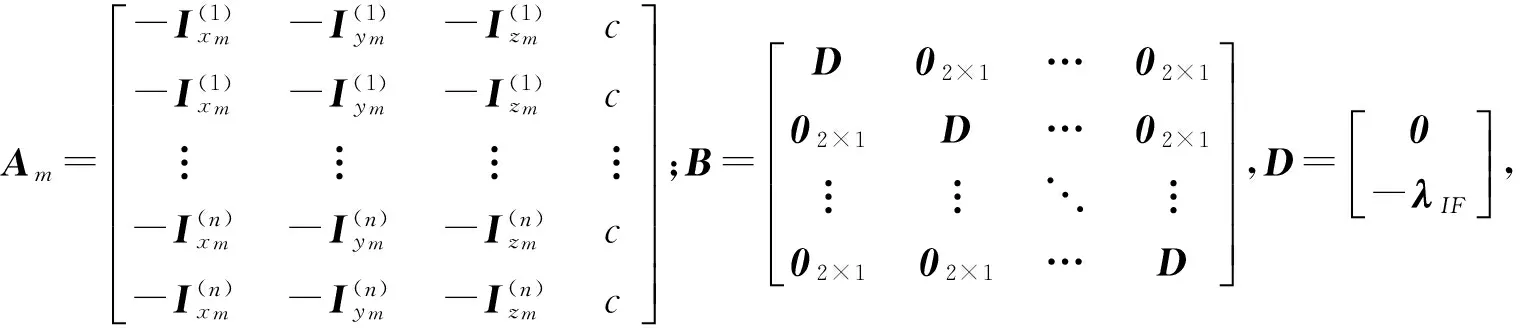
式(5)仅为单颗卫星单历元观测量线性化后组成的观测方程,若推广为在m个历元同步观测到n颗卫星的情况,则线性化后的观测方程矩阵可写为

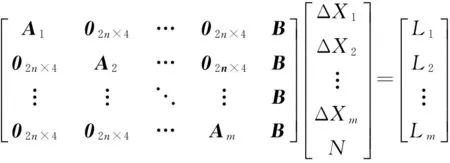
(6)

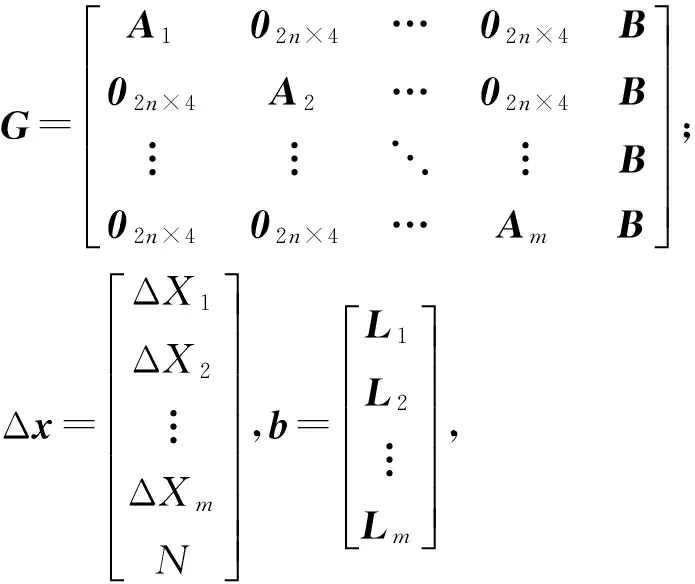
GΔx=b.

(7)

根据最小二乘计算公式,式(7)的结果可表示为

Δx=(GTG)-1GTb.

(8)

2 INS信息辅助下的精密单点定位

GPS/INS组合可有效提高导航系统的性能。INS能够保持短时间内高精度的导航信息输出,输出可以作为先验信息,辅助载波相位中整周模糊度准确、快速地解算[8]。根据导航信息的两种不同的利用方式,可将辅助方法分为位置代入法和虚拟观测量法。

2.1 位置代入法

位置代入法下的INS辅助模糊度解算是指直接利用惯导系统短时间内输出的高精度位置信息,在精密单点初始定位阶段,代替未知的流动站坐标计算卫星至接收机的几何距离并代入方程。采用该种方法可以在求解模糊度浮点解时减少方程组中未知数的个数。

根据式(6),可将位置代入法m个历元同步观测到n颗卫星时的方程改写为:

(9)

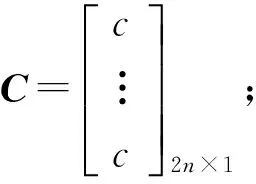
由式(9)可见,在位置代入法中,未知数只有各个历元的接收机钟差和各颗可用卫星的模糊度参数。对于单历元观测方程,虽然减少了未知数个数,但单独采用载波相位观测值会导致方程秩亏,因此仍需加入伪距观测量进行求解。对于多历元观测方程而言,对观测量和惯导信息的平差处理可以减弱测量噪声带来的影响,提高模糊度浮点解的精度。

2.2 虚拟观测量法

虚拟观测量法是指将INS输出的短时间位置信息写为与观测方程相同的形式,从而构建出“虚拟观测量方程”,进入原观测方程中与原方程进行联立,再利用最小二乘法求得模糊度浮点解[9]。

由惯导位置信息构建的虚拟观测方程可表示为

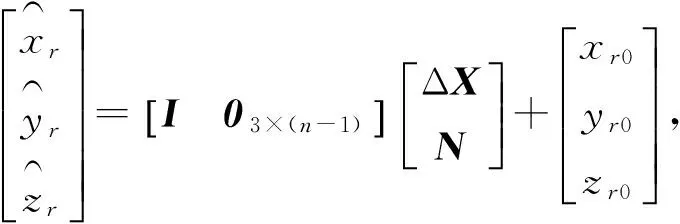
(10)

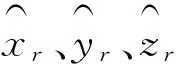
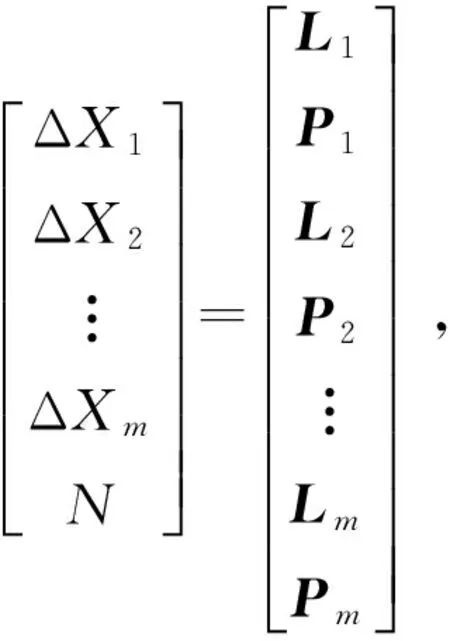
(11)

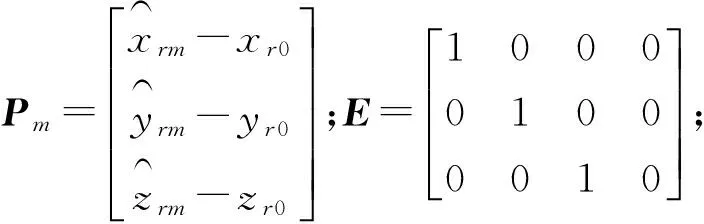
虚拟观测量法同样也可以提高模糊度浮点解的精度,下面对其进行理论推导,观察可以反映方程性质的法矩阵,即最小二乘解的协方差矩阵的逆。

位置辅助后,单历元方程GΔx=b的法矩阵为M=GTWTWG,其中W为观测量的权矩阵,则式(11)中的方程对应的法矩阵可以表示为

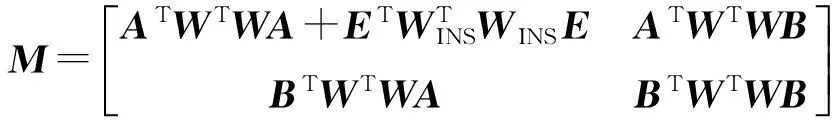
(12)

而未受辅助的式(6)中方程对应的法矩阵可以表示为

(13)

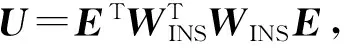
3 动态仿真场景的建立

本文采用Matlab仿真软件进行动态仿真场景的建立,生成一组动态的模拟观测量。

其中,精密星历文件为2016年4月15日真实的GPS精密星历文件。仿真参数设置为:仿真时间由2016年4月15日13点02分0秒开始,并设定历元的时间间隔为0.1 s,共1000个历元。流动站的初始坐标设定为东经116.15285494°、北纬39.81211940°、高程73.609 7 m.设流动站的初始加加速度、初始加速度、初始速度均为零,其中加加速度为加速度随时间的变化率,且流动站在东西方向运动并规定向东为正,向西为负。流动站在第0～1 s做10 m/s3的加加速运动,1～20 s内加加速度恢复为零,做匀加速运动,第20～21 s内再次做10 m/s3的加加速运动,21～30 s内加加速度恢复为零,第30～31 s内做-20 m/s3的加加速运动。第31 s后加加速度恢复为零,此后一直做匀速运动。

在生成动态模拟观测量时,卫星位置由真实精密星历进行计算,每个历元都根据接收机所在的流动站位置坐标计算其与各可视卫星之间的距离,并生成伪距观测量和载波相位观测量。添加观测量噪声时,可假设伪距和载波相位的观测量噪声均为均值为0的高斯白噪声,且伪距观测量的测量噪声标准差为0.6 m,载波相位观测量的测量噪声标准差为0.008 m.设定完毕后,生成为Rinex格式的观测文件以用于后续的算法仿真。

4 仿真分析

由文献[10]可以仿真得到:当陀螺常值偏移为[0.03°/h,0.04°/h,0.05°/h]、陀螺的白噪声均方差为0.015°/h、加速度计常值零偏为[30 μg,40 μg,50 μg]、加速度计白噪声均方差为0.25 μg时,INS在100 s内输出的三方向位置总误差在5 m以内。因此,首先取较为理想的情况进行仿真,设INS输出的位置信息误差是均值为0的高斯白噪声,且其在三个方向上的误差标准差均为0.5 m.由于仿真使用的观测量为模拟观测量,因此各历元中标准的流动站位置坐标已知,更加便于观察辅助效果。

对算法进行如2.1、2.2节所述的两种位置辅助方法的改进,改进后三种算法的位置估计结果与流动站位置之间在经度、纬度、高程三方向上的位置误差比较如图1～图3所示。

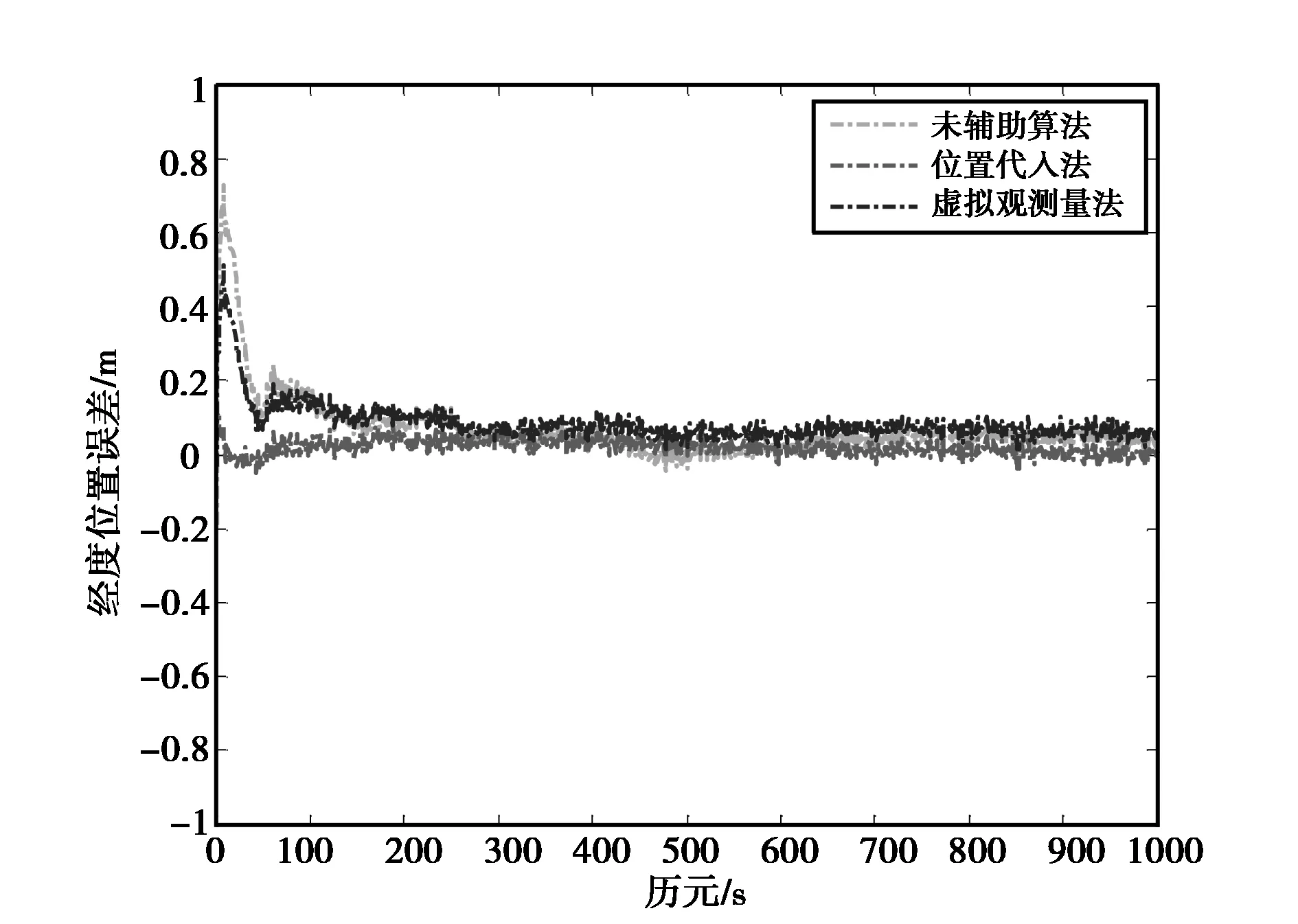
图1 经度误差比较

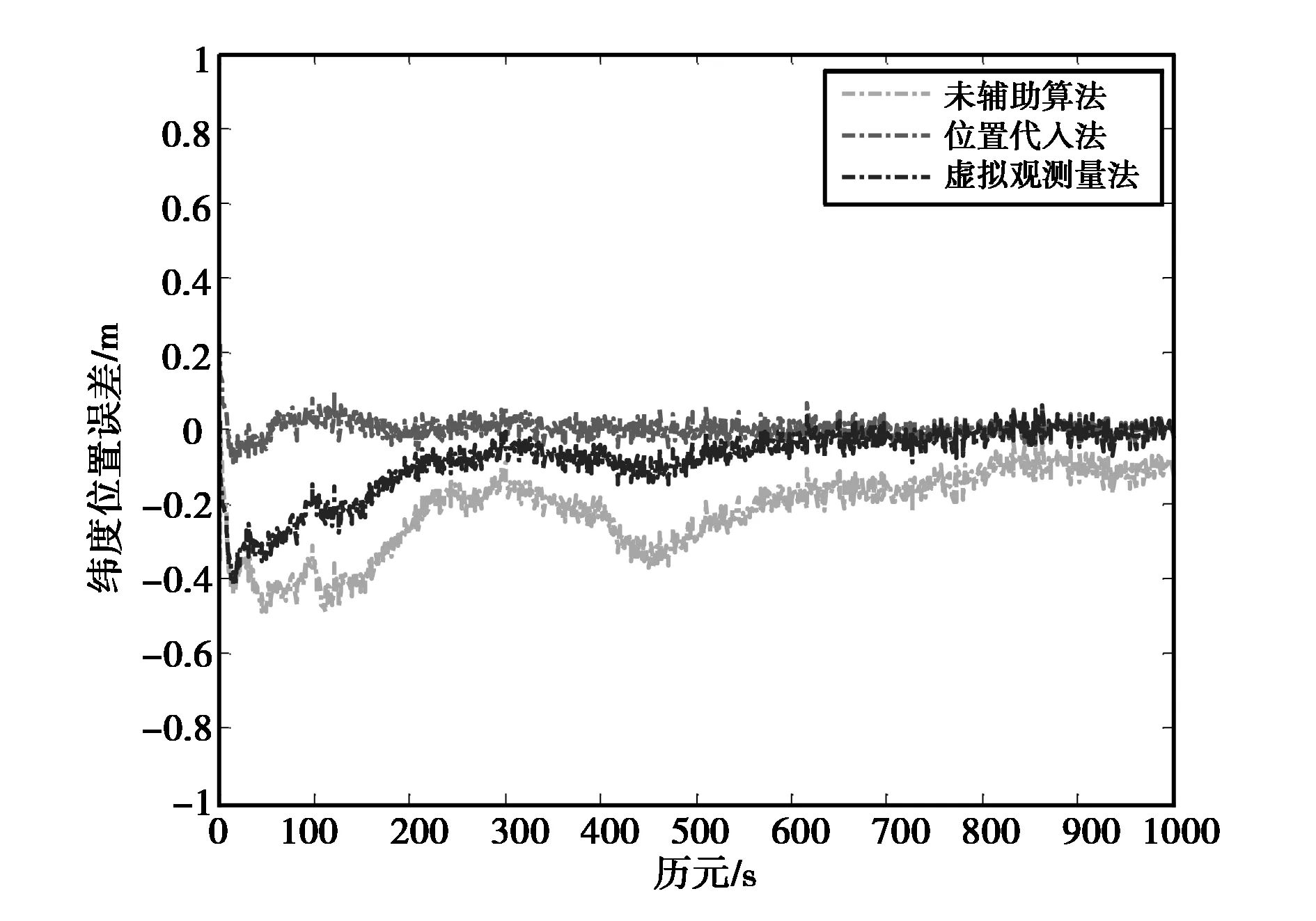
图2 纬度误差比较

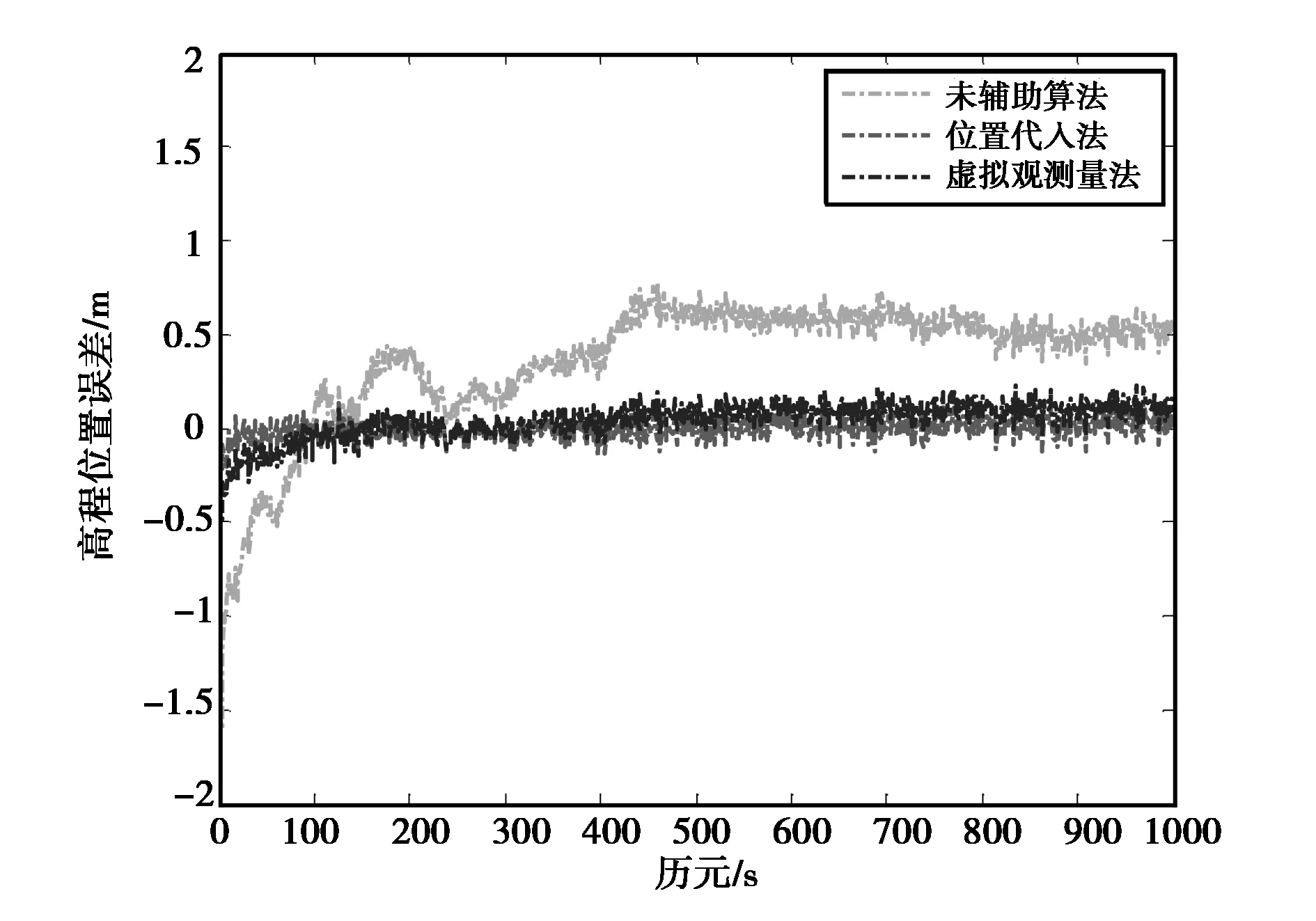
图3 高程误差比较

由图1～图3误差比较可以看出,前1 000个历元内,在位置估计精度方面,由于各历元模糊度均为此前所有历元的平均值,因此三方向上的误差均呈逐渐收敛的趋势。改进的两种算法在三方向上的位置误差较未辅助算法的位置误差均有分米级的改善作用,且位置代入法优于虚拟观测量法。在收敛速度方面,当流动站处于第0～310历元的加加速度运动状态或匀加速运动状态时,两种改进算法的位置误差收敛速度均快于未辅助算法,且位置代入法优于虚拟观测量法,可以在短时间内迅速收敛至厘米级,说明该算法更加适应于在动态场景下辅助模糊度的解算。当流动站做匀速运动时,三种算法的误差曲线均趋于平稳。

由前文可知,辅助算法能够改善定位精度,本质上是由于其提高了模糊度浮点解的精度。为了研究惯性位置误差标准差对模糊度浮点解误差标准差的影响,取INS的位置误差标准差分别为[0,0.25,0.5,0.75,1, 1.25,1.5, 1.75,2,2.25,2.5,2.75,3,3.25,3.5,3.75,4](单位: m)进行观察,三种算法在不同的惯导位置误差下的模糊度误差曲线如图4所示。

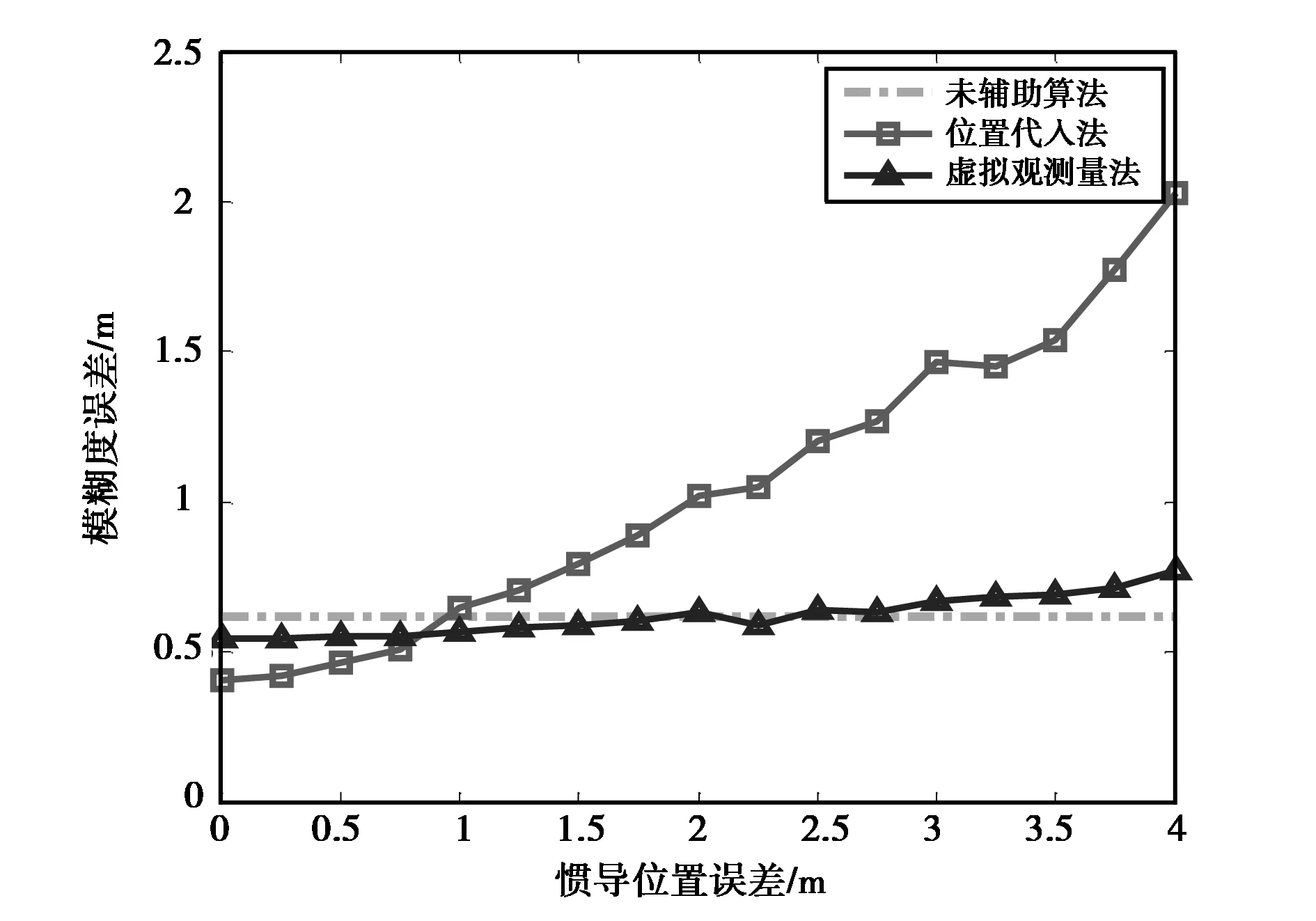
图4 惯导位置误差对模糊度误差的影响

图中,未辅助算法的模糊度误差标准差大小与惯导位置误差标准差无关,可以作为比较的基准。结合图4可以发现,当惯导位置误差标准差小于1 m时,两种改进算法所得到的模糊度误差均小于未辅助算法,能够有效提高模糊度浮点解的精度,且在位置误差标准差小于0.75 m时,位置代入法优于虚拟观测量法。当位置误差标准差大于1 m且不断增大时,位置代入法的辅助作用反而较未辅助时明显增大了模糊度浮点解的误差,且在位置误差标准差大于2.5 m后,虚拟观测量法也使得模糊度浮点解较未辅助时的精度降低,但不会使精度明显变差。总结后不难发现,当惯导位置信息误差大于伪距误差时,位置辅助的效果就会变差,即惯导对准精度越高,位置辅助的效果越明显。

5 结束语

本文充分利用了INS可在对准阶段完成后的短时间内保持较高位置精度的特点,研究了利用INS输出的位置信息对模糊度浮点解的解算进行辅助的两种最小二乘方法,分析了这两种辅助方式对模糊度浮点解求解的改善作用,并通过建立动态的仿真场景,观察了动态下两种算法的辅助效果。结果表明,两种方法各具特点。定位精度方面,位置代入法的辅助效果明显优于虚拟观测量法,可利用INS输出的短时间内高精度位置信息达到辅助模糊度准确解算、误差快速收敛的目的。惯导位置误差对模糊度误差的影响方面,虚拟观测量法优于位置代入法,能在更大的INS位置误差下依然起到辅助作用。

[1] 陈安京.GPS动态精密单点定位(PPP)研究[D].南京：东南大学,2007.

[2] 谢刚.GPS原理与接收机设计[M].北京:电子工业出版社,2012:201-202.

[3] 张晓安,何晓峰,王荔斌，等.惯性信息辅助的载波相位模糊度求解算法[J].计算机工程与设计,2010, 31(13): 3081-3083,3087.

[4] 刘景瑞.INS辅助差分GPS组合定位中的模糊度确定的理论研究及实现[D].青岛：山东科技大学,2013.

[5] 谢宏飞,郝金明,刘伟平，等.INS位置精度对GPS整周模糊度解算影响分析[J].全球定位系统, 2013, 38(1): 52-56.

[6] 赵兴旺,王胜利,刘超.GNSS精密单点定位理论与方法[M].合肥:中国科学技术大学出版社,2015:90-91.

[7] 叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学,2002.

[8] 谢宏飞.INS辅助GPS模糊度快速恢复与周跳探测技术研究[D].郑州：解放军信息工程大学,2013.

[9] 赵伟,万德钧,刘建业.一种用INS辅助GPS周跳检测和求解整周模糊度的方法[J].中国空间科学技术, 2004(2):13-18.

[10]王新龙.惯性导航基础[M].西安:西北工业大学出版社,2013.