基线长度和俯仰角约束条件下的模糊度浮点解求解及仿真实现

韩忠辉，张道成

(中国人民解放军91404部队,河北 秦皇岛 066000)

1 整周模糊度的基本概念

随着科学技术的不断发展,载波相位载体姿态的精确测量在军事、民用、商用等方面显得日益重要。我们在进行载波相位测量时,接收机实际上能测定的只是不足一整周的部分,因为载波是一种单纯的余弦波,不带有任何识别标志,所以我们无法确定正在测量的是第几个整周的小数部分,于是在载波相位测量中便出现了一个整周未知数,也叫整周模糊度。

2 整周模糊度浮点解求解技术的发展

随着GPS载波相位差分技术的深入研究,利用两个或多个接收机进行高精度的载体姿态测量成为可能。快速、准确、可靠地求解整周模糊度是载体姿态测量的关键问题之一。针对这个问题,国内外许多学者和研究人员做了大量的工作。安徽理工大学徐跃[1]针对短基线单历元解算考虑到GEO卫星模糊度较难固定问题,在宽巷模糊度固定的基础上约束固定出IGSO和MEO卫星的模糊度,然后再用IGSO和MEO卫星模糊度约束固定出GEO卫星模糊度,而固定宽巷模糊度时法方程的病态性则通过基于奇异值分解的正则化法来解决,在N、E、U方向定位精度达到厘米级。武汉大学沈明星[2]针对GNSS网络RTK参考站间三频模糊度确定进行相关研究,详细介绍了网络RTK技术中参考站间模糊度确定、误差改正数生成和流动站定位的相关理论和算法,开展了相关研究。武汉大学隋心[3]在任意GNSS系统之间、不同波长之间、不同基线长度条件下均可实现系统间双差模糊度构建和固定为目标,提出顾及系统间双差模糊度固定的多GNSS定位统一数学模型。

3 有约束条件的整周模糊度浮点解求解

在实际的姿态测量系统中,由于对实时性要求比较高,所以短时间模糊度的固定就显得非常重要,但是在较短的观测历元下,往往会出现以下几种情况:第一种情况是,由于各种噪声的影响,使模糊度浮点解精度很差,这样导致浮点解构成的模糊度搜索空间中并没有正确的整数解存在,从而导致求解失败;第二种情况是,即使模糊度真值在搜索空间中,但最后模糊度收敛值并非模糊度正确解,这时就必须利用后续历元的观测量进行计算和检验,这样就延长了模糊度固定时间;第三种情况是,由于短时间模糊度之间有非常强的相关性,使得模糊度搜索空间极其狭长,尽管Z变换后也如此,这时对于实时姿态输出系统,如何快速地搜索模糊度就显得尤其重要。

为了在短时间内得到高精度的浮点解,我们常常借助于一些额外的辅助措施[4-7],例如对于短基线姿态测量系统来说,通过事先接收机天线间的基线长度可以精确得知,一些低成本的惯性器件短时间内可以实时地给出姿态角的近似参考值,从而提高模糊度解算的成功率。在GPS短基线载波相位双差观测模型中,主要考虑两组未知数,分别是基线矢量和双差整周模糊度。为了在短时间内得到精确的姿态结果,必须利用模糊度的整数特性。LAMBDA(最小二乘降相关平差法)算法以其较好的性能和完备的理论体系得到越来越多的关注,下面给出了基于LAMBDA算法的基线长度和俯仰角约束的浮点解求解方法。

3.1 基线长度约束虚拟观测方程

在GPS定向解算算法中,固定长的基线可以提供可靠的观测信息。下面将基线长度信息融入双差方差中去。

S2=(ΔX0+dX)2+(ΔY0+dY)2+(ΔZ0+dZ)2

(1)

式中,X0等为初始基线坐标,它可以通过初始码定位或其他方法得到,S为基线长度;(dx,dy,dz)为基线的改正数向量,也是双差定位中的未知向量。展开上式有

2ΔX0dX+2ΔY0dY+2ΔZ0dZ

(2)

令dx2+dy2+dz2=K2,整理得:

(3)

其中,S0为初始基线向量的长度,K2为一大于0的变量,其精度与初始基线精度有关。将上式写成矩阵形式有

(4)

3.2 俯仰角约束虚拟观测方程

根据WGS-84坐标系与ENU坐标系的转换关系有

(5)

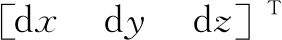
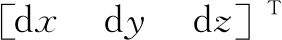
dz=S·(sin(p)-sin(p0))

(6)

式中,p0为初始基线矢量(ΔX0,ΔY0,ΔZ0)求解的初始俯仰角,p为当前估计的俯仰角,S为基线长度。所以,根据式(5)和式(6)有

S(sin(p)-sin(p0))=

(7)

3.3 浮点解方程的组建

为了提高模糊度浮点解的精度,采用载波相位、伪距、基线长度和俯仰角等信息来建立浮点解方程。具体如下

(8)

其中,A为GPS观测值的系数矩阵,AS为基线长度的系数阵,AP为俯仰角约束的系数阵,λ1为载波L1的波长,I为单位矩阵,b为未知基线向量,N为未知模糊度向量,νL1、νCA、νs、νp分别为观测值L1、CA基线长度和俯仰角的改正数;lL1、lCA为L1、CA观测值与几何距离之差;ls为基线长度与其初始值之差。

从式(8)可以看出,即使在单历元情况下,该方程也是满秩的,但是为了能够连续利用后续历元的信息,这里给出一种模糊度向量和基线向量分离的最小二乘求解方法。

假设未知向量b、N和观测值L组成的方程可以写成如下形式:

L=Ab+BN+VP

(9)

式中,A、B分别为基线向量和模糊度向量的系数矩阵,P为观测值的权矩阵。经过变换可得如下矩阵形式:

(10)

(11)

由此可见,式(11)只是关于模糊度的求解公式。在实现该模型时,由于伪距和载波相位精度有着数量级上的差距,导致载波相位观测量淹没在伪距观测量的噪声中,很难得到高精度的浮点解,所以必须合理地选取相位观测量与伪距观测量之间的权重比。另外,基线长度约束和俯仰角约束权矩阵的选择往往与先验精度有关,理论上基线矢量先验精度越高,为了在方程组中体现其作用,则对应的权重就应该越大。

4 仿真及实现

为了分析基线长度与俯仰角约束权矩阵对LAMBDA算法的影响,下面给出权的选取对模糊度成功率影响的仿真。图1中的俯仰角噪声的方差设为σ2(n)。

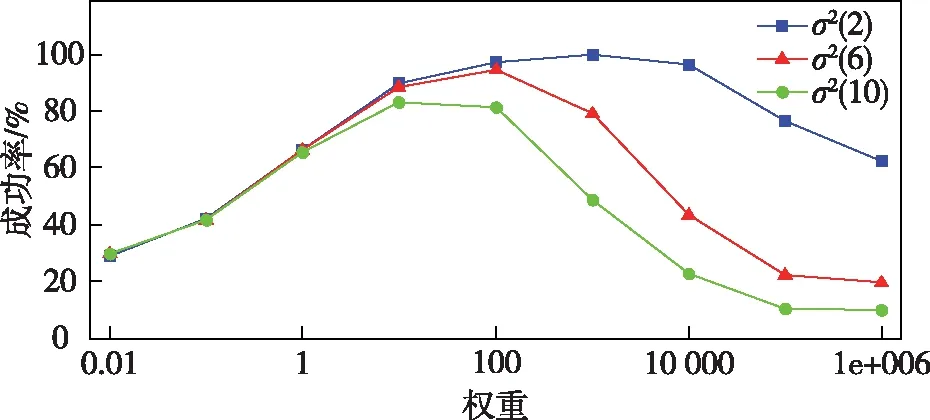
图1 基线长度与俯仰角约束权重对模糊度成功率的影响

从图1可以看出,权重的选取对模糊度的固定成功率有很大影响,对方差为2°的倾角约束误差来说,当权重取1 000左右效果最好;而且方差不同,最高成功率处的权重也不同,所以只有合理地选取约束值的权重才能使解算结果改善。

为了仿真约束条件下模糊度浮点解的精度,这里采用自编单基线GPS原始数据生成软件进行仿真。图2为单基线观测数据模拟图。仿真共用400个历元,共视的卫星ID为[1,5,6,11,12,20,21],其中主卫星采用高度角最高的1号卫星;基线长度设定为1.0 m;参与约束的俯仰角采用在俯仰角真值基础上加上方差为2°的误差,具体度数范围见图3;载波相位与伪距方差-协方差矩阵均采用单位阵模型,约束方程的载波相位、C/A码伪距、基线长度和俯仰角权重比为100 000∶2.5∶100∶100;整周模糊度真值采用全部历元解算,仿真中给出了单历元和递推历元两种解算模糊度的浮点解与模糊度真值的差值。仿真程序界面具体参见图4至图9。

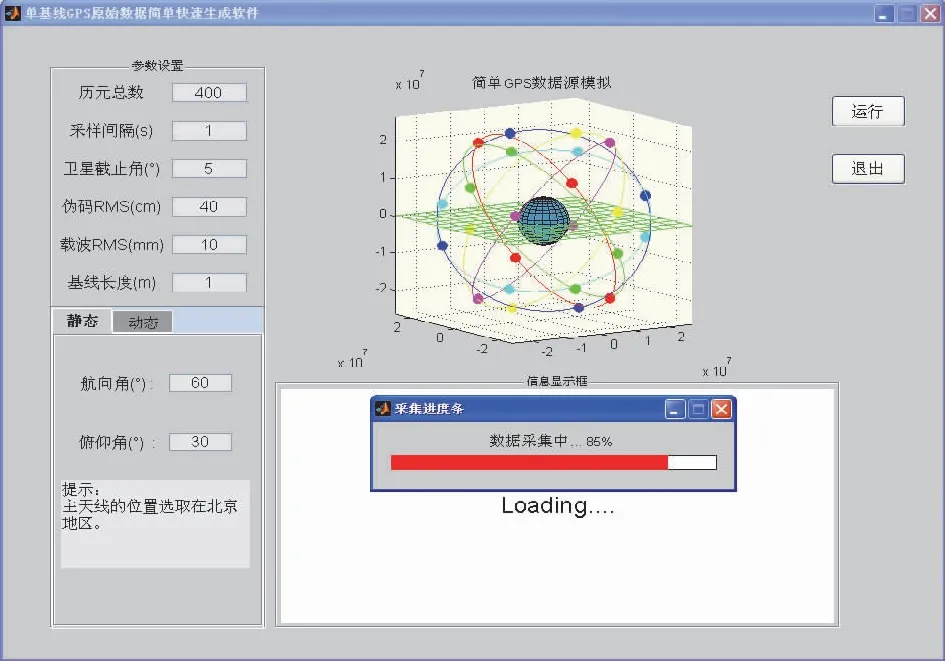
图2 单基线GPS原始数据生成软件

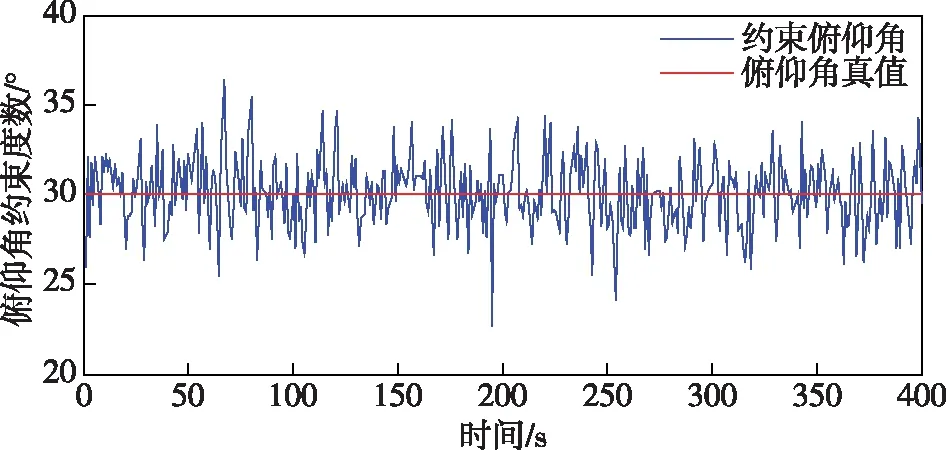
图3 约束俯仰角度数仿真图

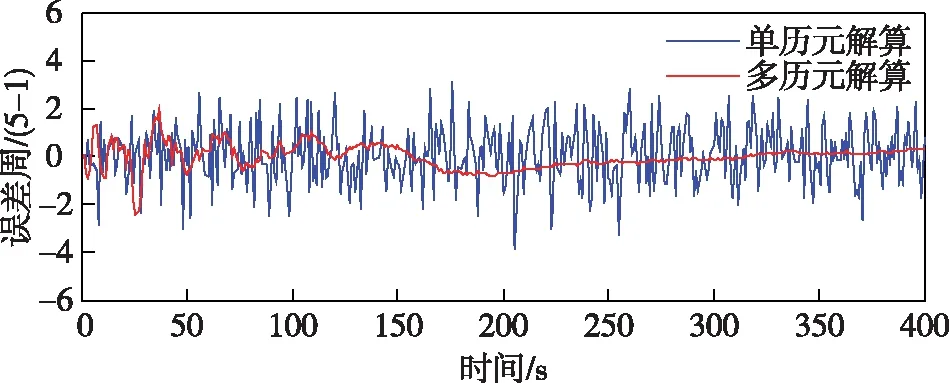
图4 卫星5-1模糊度浮点解误差图

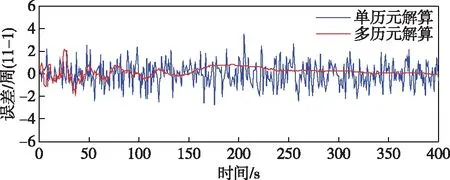
图5 卫星6-1模糊度浮点解误差图

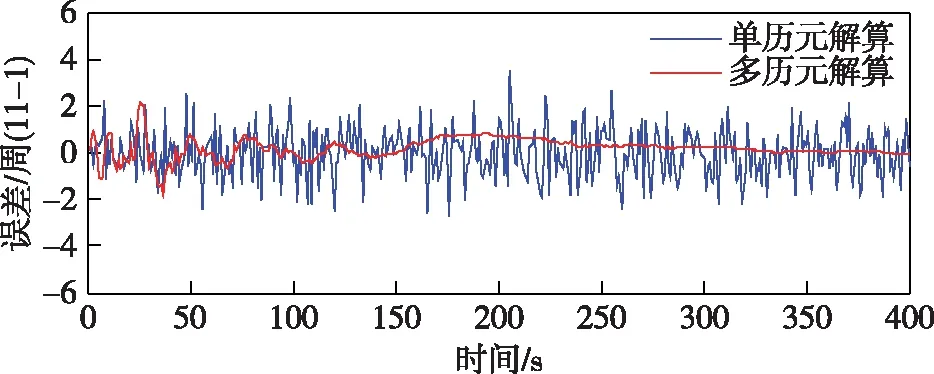
图6 卫星11-1模糊度浮点解误差图

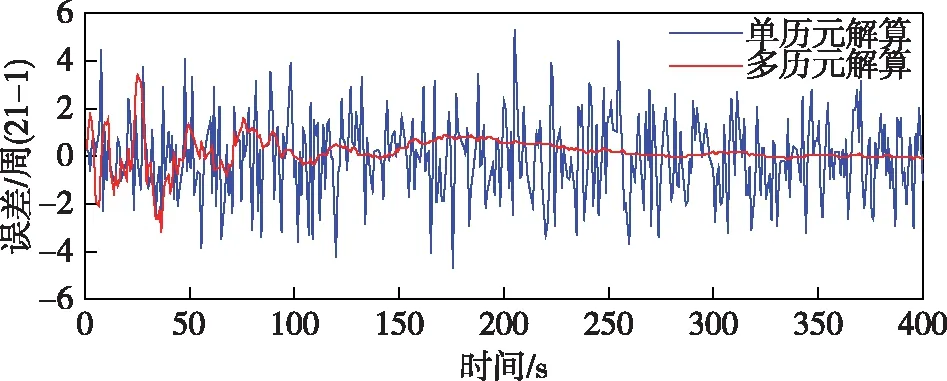
图7 卫星12-1模糊度浮点解误差图

图8 卫星20-1模糊度浮点解误差图

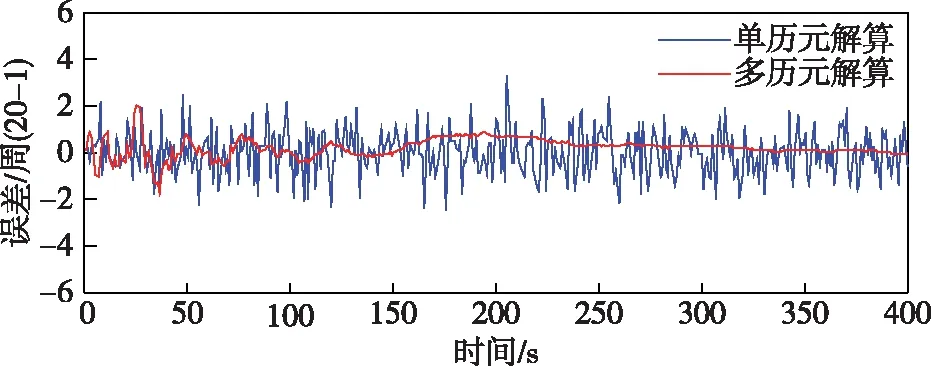
图9 卫星21-1模糊度浮点解误差图

从仿真图4到9中可以看出,无论是单历元的解算还是多历元的解算,卫星截止角分别为5、6、11时,并且浮点模糊度的浮点解精度没有太大的变化,变化不是很明显,当增加到12、20时,单历元的浮点模糊度的浮点解精度有了明显的增加,当变化为21时,浮点模糊度的浮点解精度变化不是特别明显。

但是无论截止角如何变化,当历元在0～290时,浮点的模糊值和实际的真值存在一定的差距,从模糊度浮点解误差图可以看出,单历元模糊度的浮点解糊度一般在真值±5周以内,而递推计算的模糊度浮点解精度则相对较高,它利用当前历元以及前面所有历元的观测值信息,可以看出当到300历元以后直至400历元,单历元模糊度的浮点解糊度的真值接近于0,也就是说基本上都接近模糊度固定解真值,此时可以直接对其取整即为正确的整周模糊度。

LAMBDA算法最后按照残差由小到大依次给出指定的多个候选值,前两个候选值代表“最优解”和“次优解”。如果浮点解精度足够高的话,那么第一个候选值就是真实的整周模糊度。然而,短时间内,真实的模糊度解往往不在第一个,通过对实测数据进行处理,这里进行了递推求解模糊度浮点解时的真实模糊度出现位置仿真,见图10。

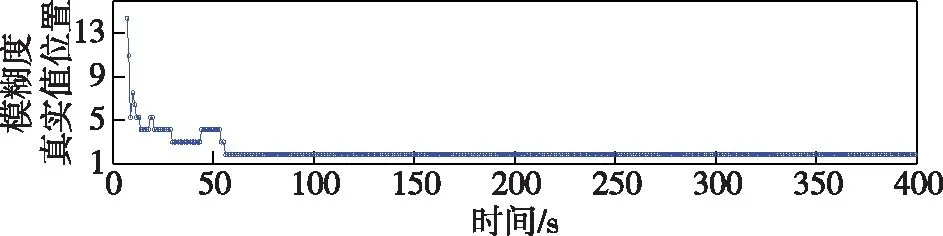
图10 递推历元下正确候选值出现的位置

从图10可以看出,模糊度真实解的位置随着时间的增加逐渐靠近“最优解”,这时因为模糊度浮点解的精度随着时间的增加而变高,所以可以通过模糊度浮点解的精度来动态的调整模糊度候选点数。当浮点解精度高于某一定值时,此时的最优解就是模糊度真实解。

5 结束语

求解整周模糊度时,依赖的浮点解精度要求很高,同时短历元求解的浮点解一般偏离真值很大,这时搜索的成功率很低。作者提出了基线长度和俯仰角约束的模糊度浮点解求解方法,并给出一种参数分离的最小二乘求解方法,该方法有利于多历元的递推解算。不难发现随着历元数的增加,浮点解的精度也逐渐增加。