高架桥在地震作用下的碰撞反应研究

鞠碧玉，秦建敏，王桂萱

（大连大学 土木工程技术研究与开发中心，辽宁 大连 116622）

0 引言

地震是一种会产生极大破坏的自然灾害，近年来地震灾害导致的人员伤亡和经济损失随着人口的增长和人员的集中变得更加惨重。在日趋发展的经济状态下，高架桥已经成为城市交通的关键部分，如果在地震中受到损坏而导致交通系统的瘫痪，将会给城市带来巨大的经济损失，也会阻碍震后人员的疏散以及抗震救灾工作的展开；另一方面，修复震后受损的桥梁这项工作也极为困难。

高架桥在地震作用下的破坏形式有很多种，其中碰撞导致的桥梁破坏占有很大比例[1]。高架桥在地震作用下的碰撞在拥挤的城市建筑中还有可能会放大结构的地震响应，并导致相邻结构的破坏，对城市建筑造成二次伤害[2]。因此，研究高架桥在地震作用下的碰撞反应及其防撞措施十分必要。

1 高架桥碰撞问题研究现状

高架桥的碰撞反应[2]主要是主梁与桥台、相邻跨的梁之间以及梁上相邻桥面板间的碰撞[3]。即地震作用下，高架桥的梁体纵向位移过大，超出了预留的伸缩缝宽度时，就会导致梁与梁之间的碰撞，从而产生梁体的损坏，这种瞬间的巨大碰撞力，还可能导致支座失效，更严重的可能会导致落梁震害。当梁体横向位移过大时，梁体与挡块或者桥台发生碰撞会导致挡块或桥台的破损[4]。

1985年墨西哥城地震之后，人们才对地震中建筑结构碰撞的问题有了广泛的关注。1992年，美国加州强震观测计划获得的多组完整的强地震作用记录是在一座位于南加利福尼亚的多跨曲线梁桥上，这组记录说明地震作用下，桥梁在伸缩缝处发生的碰撞是十分复杂的[5]。1994年的美国洛杉矶北岭大地震中，洲际5号公路大桥与震源相距14千米，仍有多处桥墩和伸缩缝发生了重大的碰撞损坏[6]。1995年的921台湾大地震中，有三十多座桥梁受损十分严重，其中一部分损坏就是碰撞导致的[7]。2008年5月12日我国汶川发生8.0级地震，有接近20座桥梁完全损坏，另有200多座桥梁受损，部分桥梁是由碰撞引发的损坏。

地震作用下碰撞给桥梁带来的严重灾害，引起众多国内外研究人员对高架桥碰撞反应的重视。R.Jankowski[8]在考虑桥梁碰撞的同时还考虑了横向运动的摩擦力和纵向的梁体间的轴力。由于横向的摩擦力可以忽略不计，因此只采用了高阻尼器来模拟横向粘结状态，同时采用包含弹簧和阻尼器的接触单元来模拟纵向的碰撞过程。Malhort[9]等人通过建立模型模拟碰撞过程，同时运用振动理论来研究直杆的杆端在碰撞过程中的碰撞时间、能量耗散和力学机理。该研究的结果显示，桥梁的碰撞过程包含两个部分：接触与分离。

国内对碰撞问题也有一些研究，邢誉锋[10]利用模态叠加法对有限长Timoshenko梁在受到质点碰撞冲击瞬间的动态响应特征进行了分析研究，探讨了纵波和剪切波对梁的影响；王东升[11]等人在建立模型时用碰撞弹簧来研究邻梁的碰撞问题，并分析了邻梁碰撞所涉及的弹簧刚度比、阻尼比等参数对碰撞过程的影响；王军文[12]等人针对地震作用下，连续梁桥的伸缩缝处的碰撞现象，在考虑墩柱弹塑性以及支座的非线性基础上创建了3自由度碰撞模型，并选用了非线性时程分析方法研究地震作用下（纵向）伸缩缝的碰撞反应以及相邻联的不同向振动；刘鹏[13]等人对地震作用下的桥梁碰撞分析方法进行了改进，并证明该方法比Hertz-damp模型和Hertz模型求解方法更合理；穆翠玲[14]等人针对地震作用下复杂的桥梁碰撞问题提出了一个简便的计算方法即等效位移阻尼法，并给出了公式，对比有限元分析验证了其准确性。李忠献[15]等人研究得出了地震作用下桥梁碰撞分析的Kelvin模型的参数确定方法，并确定该模型的碰撞刚度、相邻梁碰撞恢复系数对城市桥梁的合理取值范围应该分别为：3×105kN/m~6×105kN/m和0.7~0.95。

2 桥梁碰撞问题分析方法

地震作用下桥梁的碰撞是一个短暂又复杂的问题[16]。在这个短时的碰撞过程中，桥梁发生了横向摩擦、纵向碰撞带来的变形、开裂等一系列的力学行为。国外的学者首先对这一问题进行了分析研究，目前提出的方法主要是恢复系数法和接触单元法。

2.1 恢复系数法

恢复系数法是最为基础的一种方法。该方法主要依据动量守恒定律，假定两个质点的碰撞为质心碰撞且忽略其碰撞过程，并将碰撞之后两质点的相对分离速度与碰撞接触之前的相对接近速度的比值定义为恢复系数。碰撞后的速度是根据质点碰撞前的速度以及恢复系数得出。其公式为

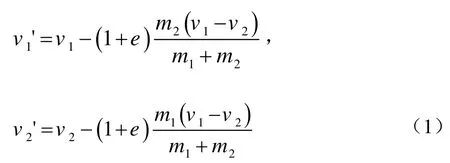
恢复系数法的原理简单易懂，其算法也比较简便[17]，通常被用来处理刚体之间的碰撞。由于恢复系数法忽略了碰撞时结构的压缩变形，因此对于刚度及弹性模量都比较大的碰撞问题，如果将其碰撞看作是瞬间完成的，那么不考虑碰撞的瞬时应力和结构变形就比较合理。但是当碰撞的结构质量较大而弹性模量较小时，如果碰撞时间长，那么结构就有可能发生比较大的变形，此时的瞬时应力和结构变形就不可忽略。此外，恢复系数法不是基于力的方法，与目前的结构分析软件难以结合。

2.2 接触单元法

接触单元是由弹簧或者弹簧和阻尼器构成的，接触单元的刚度通过弹簧来模拟，碰撞过程中的能量耗散通过阻尼器来模拟。接触单元法是通过两个点对点的接触单元来模拟相邻两节点之间的碰撞[18]。这种方法容易理解，算法比较简单，通常被用来模拟指定的两个节点之间的碰撞过程，现主要用于分析建筑结构和桥梁结构的碰撞。

（1）线性弹簧模型[19]。线性弹簧模型只由一个连接弹簧构成，是接触单元模型中最简单的模型，但是这种接触单元模型并没有考虑碰撞中能量的损耗。

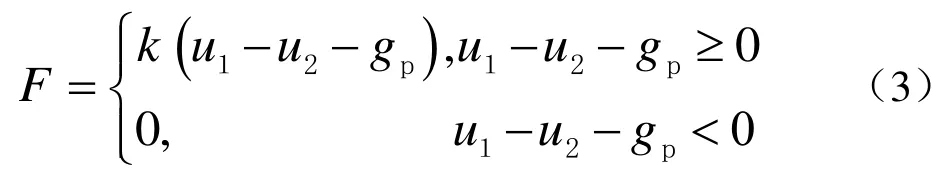
（2）Kelvin模型[8,20]。一个连接弹簧和阻尼器并联构成了 Kelvin模型，这种模型考虑到了地震作用下碰撞中能量的损耗。

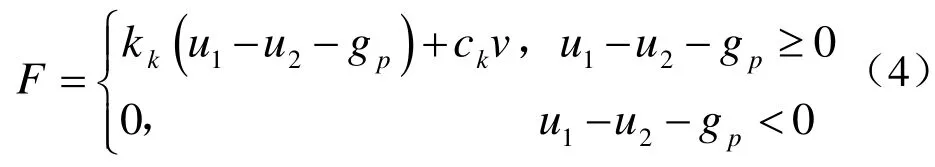
其中

（3）Hertz模型[21]。Hertz模型也是由一个连接弹簧构成，但其区别于线性弹簧模型的一点是其连接弹簧是非线性的，可以更真实地模拟碰撞过程中碰撞力与变形的关系，但是这种接触单元模型也没有将碰撞中的能量损耗考虑在内。

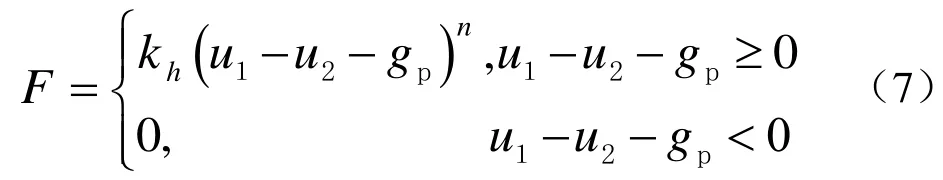
（4）Hertz-damp模型[22,23]。Hertz-damp模型将一个非线性阻尼器与Hertz模型的连接弹簧并联。此模型考虑了碰撞过程中的能量损耗。

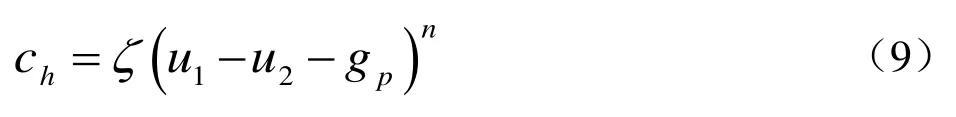
（5）三维接触－摩擦模型。以上的四种接触单元模型都没有考虑到地震碰撞时邻跨桥梁接触面上的摩擦现象，所以由此得出的地震碰撞反应的结果会存在一些误差。三维接触－摩擦模型建立在点面接触理论的基础上，同时考虑了边界渗透，可以模拟相邻梁体间的任意碰撞，但是需要耗费大量的时间来确定接触对，因此这种方法也没有得到更普遍的使用。

3 防撞措施

3.1 选取合理的邻梁间隙

在设计桥梁时，考虑到混凝土的收缩和徐变导致的桥梁上部结构的伸长或缩短，会在桥梁需要的部分设置伸缩缝。在地震作用下，梁体产生的位移在伸缩缝宽度内则避免了碰撞；若梁体的位移超过了伸缩缝宽度则会产生碰撞。所以在桥梁设计阶段，就应该充分的考虑到地震作用下梁体间产生的位移，选取合理的邻梁间隙，避免因为伸缩缝的间隙不足而引发的梁体碰撞情况。

研究表明[4]，当邻梁间隙比较小的时候，碰撞的几率会增大且碰撞的次数增多,但是碰撞力会不断减小；当邻梁间隙增大时，碰撞的几率会减少，碰撞力会增大。当间隙值增大到足以避免地震作用下桥梁碰撞时，梁体位移、墩底弯矩和剪力都会处于一个较稳定的状态，不再受碰撞的影响。但是伸缩缝如果取值过大，就会影响到桥上行车的稳定性，因此，邻梁间隙的取值应视实际情况而定。

3.2 使用耗能装置

在桥梁上安装耗能装置，可以有效的降低地震作用下高架桥的碰撞反应，从而减少桥梁的损伤。

3.2.1 缓冲装置

缓冲装置增加了梁体的阻尼，当相对位移达到缓冲装置的最大变形时，碰撞力完全由缓冲装置承受[4]。为了避免梁体间的直接碰撞和限制梁的纵向位移，桥梁抗震设计规范中明确规定了在 7度及其以上地区的梁之间、梁与桥台胸墙之间需要安装缓冲装置如橡胶垫或者其它弹性衬垫。

3.2.2 阻尼器装置

与阻尼器相比，缓冲装置成本较低，但是其随着时间老化的速度比较快。实验表明[20,24]，安装复合式金属阻尼器或粘滞阻尼器之后的桥梁碰撞力明显减小，支座的位移也大幅下降，桥梁的动力响应也随着降低。

4 结语

国内外已经有很多学者研究地震作用下高架桥的碰撞反应，并不断地改进模型和分析方法。但是，由于地震中桥梁的碰撞过程十分复杂，尤其是非线性地震反应分析更是涉及到诸多问题，在进行模拟时，往往会提出一些限制条件，这就影响了模拟计算的精度和准确性。因此，对于高架桥碰撞反应机理、模拟方法以及防撞措施还需要更深入的研究。另外，现阶段的模型还比较单一：一般为截面单一、墩柱高度相同并且形状较为规则的梁式桥，无法对城市现有的复杂高架桥进行分析。因此，需要对以往实际地震中大型高架桥碰撞反应进行更深入的分析，同时结合振动台试验及有限元分析软件，提高碰撞模型的计算精度。

[1]岳福青. 地震作用下隔震高架桥梁的碰撞反应及控制[D].天津大学, 2007.

[2]于海龙, 朱晞. 地震作用下简支梁桥梁间碰撞的反应性能[J]. 北方交通大学学报, 2004, 28(1): 43-46.

[3]王东升, 冯启民, 凌贤长, 等. 桥梁非线性地震反应分析若干问题研究现状[J]. 地震工程与工程振动, 2002(01): 61-66.

[4]郭磊. 强震作用下桥梁的碰撞效应及对应措施[D]. 湖南大学, 2010.

[5]Malbotra P K, Huang M J. and Shakal A F. Seismic interaction at separation joints of an instrumented concrete bridge[J]. Earthquake Engineering and Structural Dynamics,1995, 24(2): 1055-1067.

[6]Northridge earthquake reconnaissance report, Vol.1[R].Earthquake Engineering Research Institute (EERI), Oakland,Calif, 1995, Rep. No. 95-03.

[7]. Chi-Chi. Taiwan earthquake reconnaissance report[R].Earthquake Engineering Research Institute (EERI), Oakland,Calif, 2001, Rep. No. 01-04.

[8]Jankowski R, Wilde k, Fujino Y. Pounding of superstructure segments in isolated elevated bridge during earthquakes[J].Earthquake Engineering and Structural Dynamics, 1998,27(1): 487-502.

[9]Malhotra P K. Dynamics of seismic pounding at expansion joints of concrete bridges[J]. Journal of Engineering Mechanics, 1998, 7(1): 794-802.

[10]邢誉峰. 有限长Timoshenko梁弹性碰撞接触瞬间的动态特性[J]. 力学学报, 1999(01): 68-74.

[11]王东升, 冯启民, 王国新. 基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J]. 工程力学, 2004(02):157-166.

[12]王军文, 李建中, 范立础. 连续梁桥纵向地震碰撞反应参数研究[J]. 中国公路学报, 2005(04): 42-47.

[13]刘鹏, 郑凯锋, 杨雷. 地震作用下的桥梁碰撞分析改进求解方法[J]. 公路交通科技, 2011(03): 76-81.

[14]穆翠玲, 王文俊, Huimin Mu. 非线性地震荷载作用下桥梁碰撞的等效位移阻尼法[J]. 中山大学学报: 自然科学版,2006(05): 42-46.

[15]李忠献, 岳福青, 周莉. 地震时桥梁碰撞分析的等效Kelvin撞击模型[J]. 工程力学, 2008(04): 128-133.

[16]高玉峰, 李晓斌, 杨永清. 桥梁结构地震碰撞问题理论分析模型及试验研究进展[J]. 应用力学学报, 2010(04):809-816+858.

[17]顾月根. 桥梁碰撞问题的研究现状[J]. 价值工程, 2010,29(4): 160.

[18]李辉. 高墩桥梁地震碰撞效应研究[D]. 吉林大学, 2009.

[19]Maison B F, kasai K. Analysis for type of structural pounding[J]. Journal of Structural Engineering ASCE, 1990,116(04): 957-977. DOI: 10.1061/(ASCE)0733-9445(1990)116: 4(957).

[20]Anagnostopoulos S A. Pounding of buildings in series during earthquakes[J]. Earthquake Engineering & amp;Structural Dynamics, 1988, 16(03): 443-456.

[21]Pantelides C P, Ma X. Linear and nonlinear pounding of structural systems[J]. Computers & Structures. 1998, 66(1):79-92.

[22]Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. ASME, Journal of Applied Mechanics, 1975, 42(2): 440-445.

[23]Muthukumar S, DesRoches R. A Hertz contact model with non-linear damping for pounding simulation[J]. Earthquake Engineering and Structural Dynamics, 2006, 35(7): 811-828.

[24]李勇. 非一致地震激励下高架连续梁桥动力响应与控制研究[D]. 北京工业大学, 2012.