基于Hankel行列式的一类双和恒等式
宋旭霞
(呼伦贝尔学院数学统计学院 内蒙古 海拉尔 021008)
关于孤子理论中的双线性方程的研究,国际上一直非常活跃.尤其在双线性方程的群射 Lie代数的问题研究上,更为积极。事实上,应用群论的方法已经发现了许多新的孤子方程,但是这种方法需要比较高深的代数知识,应用起来也比较困难,而方程的求解过程与Hankel行列式的性质密切相关。为此,本文在已获得的Hankel行列式的双和恒等式的基础之上,研究Hankel行列式的双和恒等式的推广形式。
1.基础知识
1.1 如果行列式满足则称之为 Hankel行列式。显然,Hankel行列式满足 aij= aji的条件,因此 Hankel行列式是对称的,同时也满足条件所以它也是次对称的。
一般情况下,我们采用单后缀的方式来表示元素,令则有


1.2 若函数满足关系式则称函数关于其变量是s次齐次的;若函数满足关系式则称函数关于其变量的下标之和是s次齐次的。


1.4 已有性质
引理1[]]:关于Hankel行列式的凝聚余子式满足以下关系式:

引理2[1]:关于Hankel行列式有下列双和恒等式成立:

引理3[1]:欧拉定理:
(1)如果变量是相互独立的,函数对每一个变量都是可微的,且对于变量是s次齐次的,则有

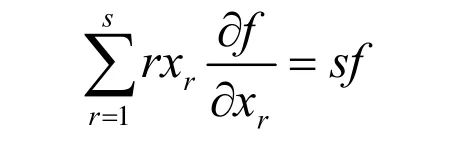
2.预备定理
Hankel行列式因其形式简洁美观、应用广泛而著称,在Hankel行列式性质研究的过程中,为了将已有Hankel行列式的双和性质顺利推广,作为基础,我们需要先行证明下列引理。
引理4:对于 Hankel行列式满足下列齐次性的而相关结论:
(1)的展开式中的每一项都是n次齐次的;的展开式中的每一项的下标之和都是 n ( n - 1 )次齐次的。
(2) Hankel行列式的代数余子式 Aij的展开式中的每一项都是 n - 1 次齐次的;它的展开式的每一项的下标之和都是次齐次的。
证明:(1) 因为 An的展开式中一共包含 n !项,每一项的形式均为这里为1,2…n的一个排列,显然展开式中的每一项都包含n个元素,从而 An是n次齐次的。
同时,通过观察展开式的每一项的形式,可以发现其下标之和为

所以,展开式中的每一项的下标之和都是 n ( n -1)次齐次的。
(2)因为 Aij是在 An中去掉了第i行和第 j列,其展开式中一共包含(n - 1 )!项,每一项的形式为
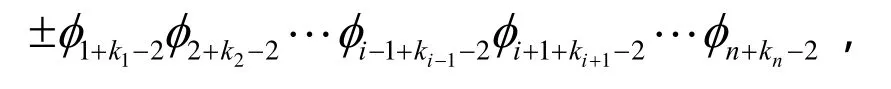
同时,可以发现每一项的下标之和为

所以,展开式中的每一项的下标之和都是次齐次的。
推论1:对于Hankel行列式的代数余子式 Aij,hk,可知 Aij,hk的展开式中的每一项都是 n - 2 次齐次的;Aij,hk的展开式中的每一项的下标之和都是次齐次的。
证明:因为 Aij,hk是在 An中去掉了第 i, j行和第 h , k列,其展开式中一共包含(n - 2 )!项,每一项的形式为

这里的一个排列,显然每一项都包含 n - 2 个元素,从而 An是 n - 2 次齐次的。同时,每一项的下标之和为

所以,展开式的每一项的下标之和都是次齐次的。


3.一类推广的Hankel行列式双和恒等式

有下列等式成立:




(2)令 m = r + s - 2 ,并且重新排列和式,则(1)式可以变形为

(4)令 m = r + s - 2 ,并且重新排列和式,则(2)式可以变形为




证明:(1) 由引理4可知 Aij的展开式的每一项都是 n - 1 次齐次的,利用Hankel行列式中对元素的偏导数的定义及欧拉定理可知

(2) 由引理4可知 Aij的展开式的每一项每一项的下标之和都是次齐次的,利用Hankel行列式中对元素的偏导数的定义及欧拉定理可知

(3)由引理4的推论1可知 Aij,hk的展开式的每一项都是 n - 2 次齐次的,利用Hankel行列式中对元素的偏导数的定义及欧拉定理可知

(4)由引理4的推论1可知 Aij,hk的展开式的每一项的下标之和都是次齐次的,利用Hankel行列式中对元素的偏导数的定义及欧拉定理可知

(5)利用Hankel行列式的性质,我们可知有


通过文中定理一和定理二的猜想与证明,我们得到了推广后的Hankel行列式双和恒等式的形式,解决了一类性质比较复杂的Hankel行列式所满足的双和关系的性质。它比Hankel行列式原有的应用空间更为广泛,不仅对于研究掺杂特殊元素的Hankel行列式的相关性质有所帮助,更为重要的是可以用它来解决Dale方程、Toda方程、Kay-Moses方程等一系列物理方程的求解问题[3-5],在可积系统的研究过程中具有非常重要的的应用价值。参考文献:
[1]Robert Vein,Paul Dale。Determinants and Their Applications in Mathematical Physics [M].Springer-verlag,1998.
[2]胡星标.孤子理论中的直接方法[M].北京:清华大学出版社,2008.
[3]荣赶丁. Cantor序列及其差分序列的Hankel行列式[D].华中科技大学,2013.
[4]文志雄,武文.Cantor序列的Hankel行列式[J].中国科学:数学,2014,(10):1059-1072.
[5]李彦君,杨胜良.加权Motzkin序列的Hankel行列式[J].纯粹数学与应用数学,2017,(01):26-36.
[6]李小飞.一类解析函数类的Hankel行列式的上界估计(英文)[J].数学理论与应用,2013,(04):23-28.

