不同权的Bloch型空间之间的加权复合算子再刻画

范海霞,席利华,张学军

(湖南师范大学数学与计算机科学学院,湖南长沙410006)

不同权的Bloch型空间之间的加权复合算子再刻画

范海霞,席利华,张学军

(湖南师范大学数学与计算机科学学院,湖南长沙410006)

本文研究了单位圆中从空间βL到βα的加权复合算子uCφ为有界算子和紧算子的条件.利用阶估计等方法,获得了有界性和紧性的简捷充要条件,推广了叶善力的相应结果.

有界性;紧性;加权复合算子;Bloch型空间;单位圆

1 问题的引进和定义

设D是单位圆,H(D)表示D上的解析函数全体,H∞表示D上的有界解析函数类,并赋以范数||f||∞=sup{|f(z)|:z∈D};dv为标准体测度,满足

设α＞0,α-Bloch型空间βα和对数权Bloch型空间βL分别定义如下:

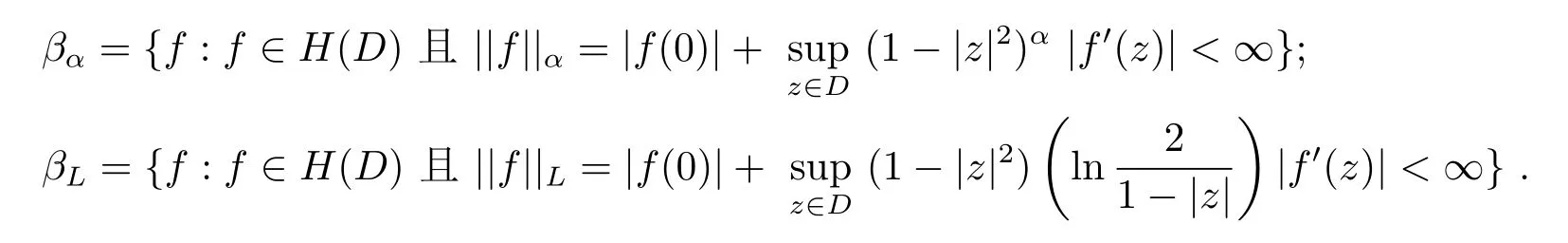
设γ＞-1和p＞0,D上加权Bergman空间定义如下:

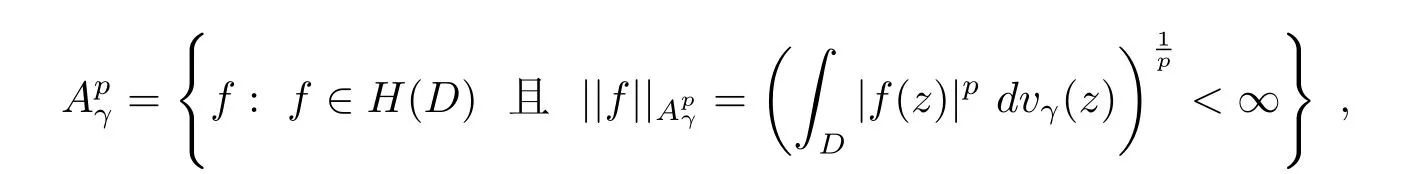
这里dvγ(z)=cγ(1-|z|2)γdv(z),常数cγ满足dvγ(z)=1.当γ=0时就是Bergman空间Ap.

设u∈H(D),φ为D上的解析自映射,X和Y为两个解析函数空间,则X到Y的加权复合算子uCϕ定义如下:

当u(z)=1时就是复合算子Cϕ;当φ(z)=z时就是乘子算子Mu.

在上世纪九十年代,Madigan和Matheson在文献[1]和[2]中研究了D上Lipschitz空间、Bloch空间和小Bloch空间上复合算子Cϕ的有界性和紧性问题,他们证明了Cϕ在Bloch空间上总是有界的和Cϕ在小Bloch空间上有界当且仅当φ在小Bloch空间中等结论;在2000年,史济怀先生和罗罗博士在文献[3]中将Bloch空间的结论推广到了Cn中的齐性域上;接下来在2001年,Ohno和赵如汉在文献[4]中就Bloch空间和小Bloch空间讨论了加权复合算子的有界性和紧性,给出了比较完整的结果;在2003年,张学军在文献[5]中讨论了p-Bloch空间和q-Bloch空间之间加权复合算子为有界算子和紧算子的条件,获得了较好的结果但尚不完整;在2007年,叶善力在文献[6]中探讨了单位圆中对数权Bloch型空间βL与α-Bloch型空间βα之间加权复合算子的问题,他给出了如下结果.

定理A设α＞0,u在单位圆D上解析,φ是D上的解析自映射,则uCϕ是βL到βα的有界算子之充要条件为

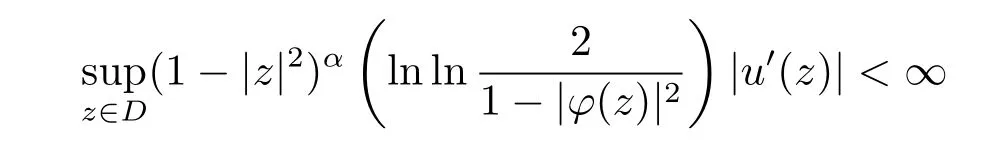
且

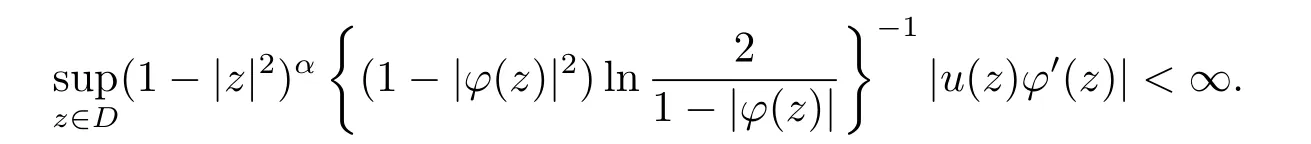
定理B设α＞0,u在单位圆D上解析,φ是D上的解析自映射,uCϕ是βL到βα的有界算子,则uCϕ是βL到βα的紧算子之充要条件为

且

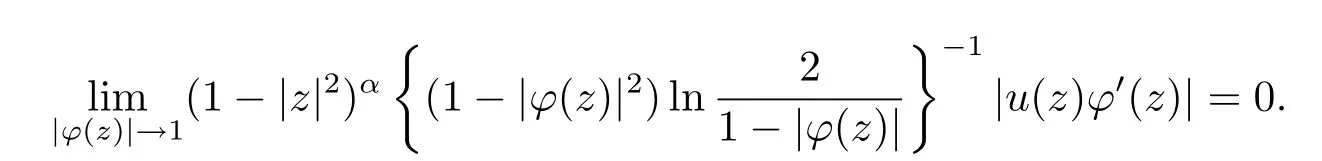
实际上,当α＜1时上述两定理讨论的是大空间到小空间的问题,若φ为D上的自同构,则u必须恒为0,真正意义较大的是α≥1时,在讨论中发现,当α＞1时定理A和定理B中的这两个条件不是独立的.另外,紧算子的确先是有界算子,但有界性也是要通过u和φ满足一定条件来刻画的,所以定理B中可以不必先给一个有界性的先决条件,而是通过u和φ直接进行刻画,如果||φ||∞＜1的话,定理B中后两个条件是不存在的,因而紧性条件可以视||φ||∞＜1和||φ||∞=1而定.本文的主要工作就是给出了α＞1时,定理A中较简捷的充要条件和定理B中不同的充要条件.

本文中c、c1、c2、c3等表示与变量z、w等无关的常数,为方便起见,不同的位置可以表示不同的数.

2 引理和主要结果

引理2.1设α＞1,u在D上解析,φ是D上的解析自映射.

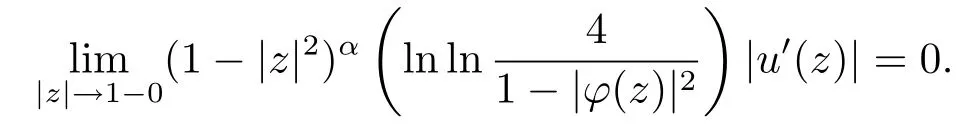
证(1)因为当0≤x＜1时,

且连续,又

这样就有

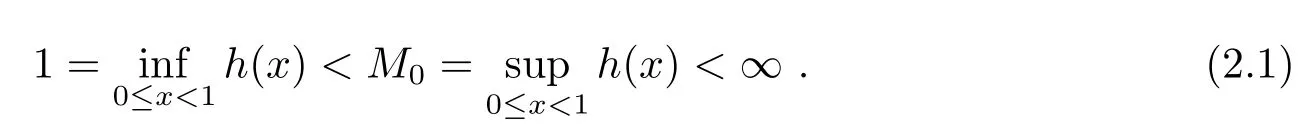
此外,对任何复数|ξ|≥1,就对数主支(ln1=0)有

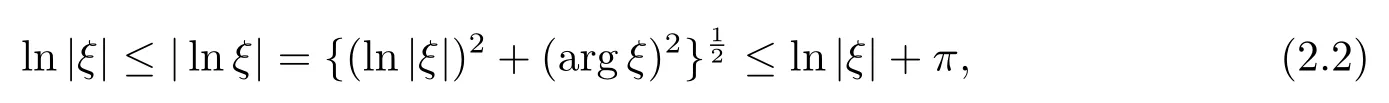
以及对任意z∈D和k≥2有

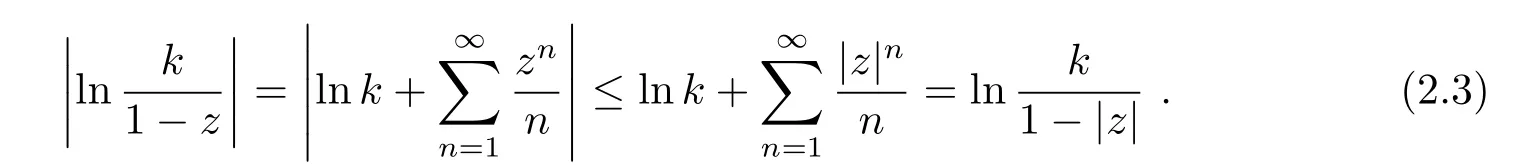
由上式和(2.1)–(2.3)式知

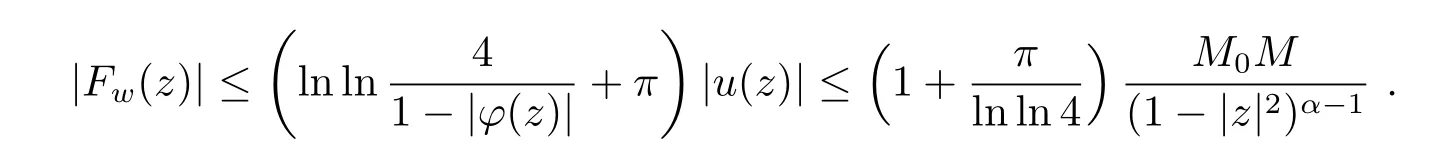
这样对一切γ＞α-2有Fw∈由文献[7]中的定理2.2(n=1的情形)知

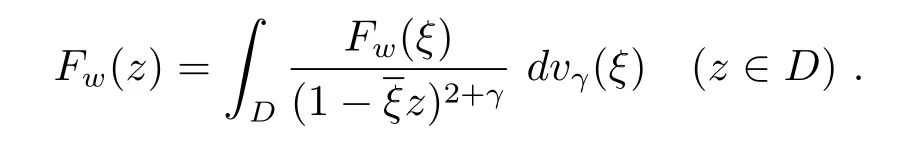
根据文献[8]中命题1.4.10(n=1的情形)可得

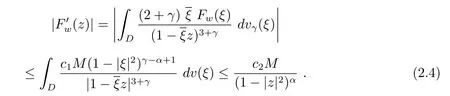
在(2.4)式中取z=w经过计算并结合Pick引理可得

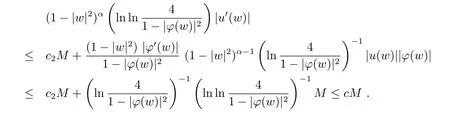
由w的任意性可知

当|ξ|≤r0时,由(2.2)–(2.3)式应用到(1)中的Fw可得

根据(2.6)–(2.7)式和文献[8]中命题1.4.10(n=1的情形)有

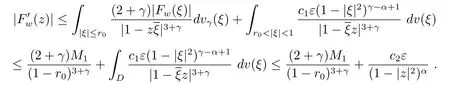
当r0＜|w|＜1时,在上式中取z=w经整理就有

从而

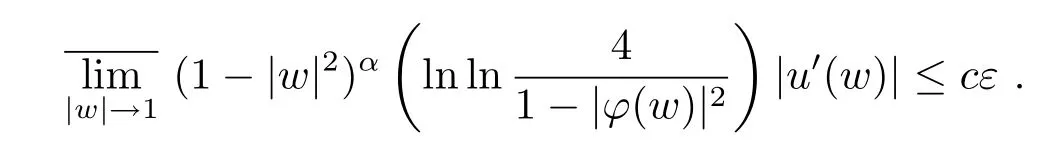
由ε的任意性可知

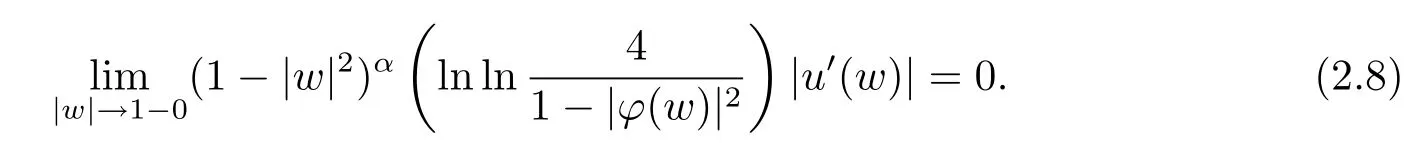
定理2.2设α＞1,u在单位圆D上解析,φ是D上的解析自映射,则uCϕ是βL到βα的有界算子之充要条件为

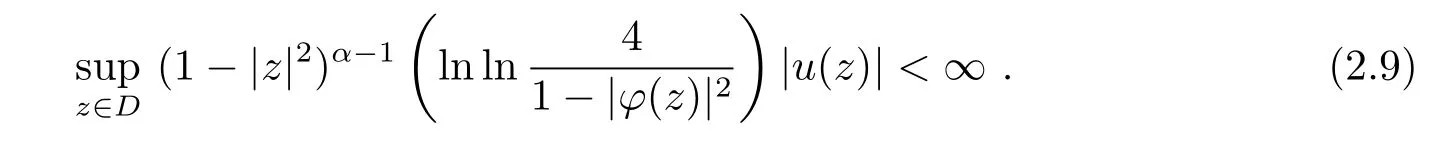
证若(2.9)式成立,设

对任意f∈βL,由文献[6]中的引理2.1、Pick引理以及(2.9)式和引理2.1中的(2.5)式可得

这样可得

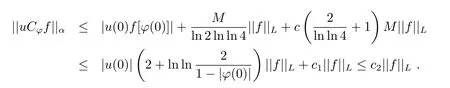
因此uCϕ是βL到βα的有界算子.反之,若uCϕ是βL到βα的有界算子,则||uCϕf||α≤||uCϕ||.||f||L对f∈βL成立.

对任意w∈D,取

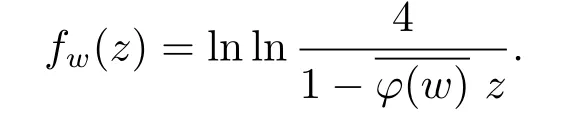
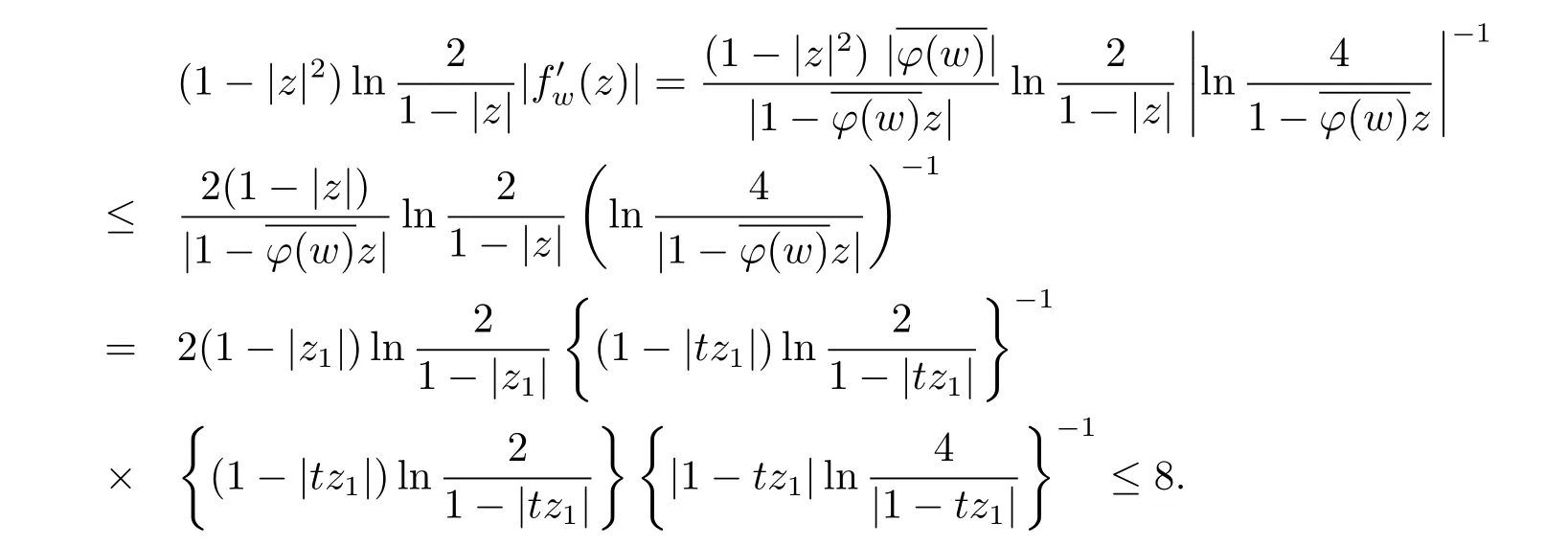
这样||fw||L≤8+lnln4.因此||uCϕfw||α≤(8+lnln4)||uCϕ||.再由文献[5]中引理2.3可得,对一切z∈D有

在(2.10)式中取z=w就有

根据w的任意性可知(2.9)式成立.

定理2.3设α＞1,u在单位圆D上解析,φ是D上的解析自映射,则uCϕ是βL到βα的紧算子之充要条件为:当||φ||∞＜1时u∈βα;当||φ||∞=1时u∈βα且

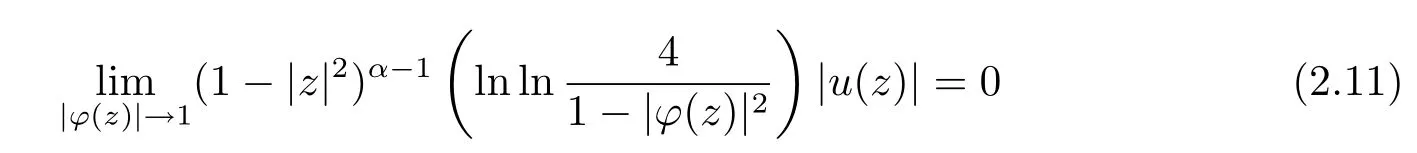
和

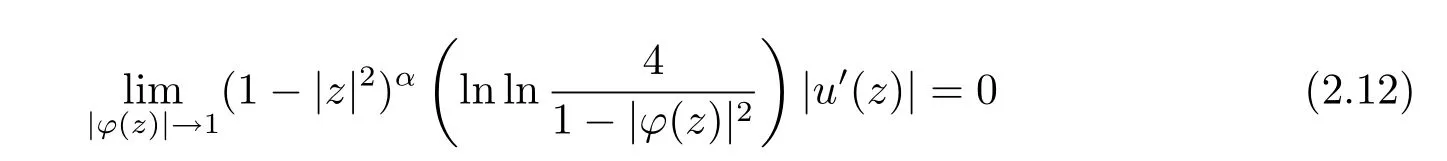
同时成立.

证若uCϕ是βL到βα的紧算子,取f=1∈βL,立即可得u∈βα.

当||φ||∞=1时,设{zn}⊂D是任意一个使得|φ(zn)|→1(n→∞)的序列,令

则{fn}在D的任一紧子集上一致收敛于0,且利用(2.1)–(2.3)式以及文献[6]中引理2.3–2.4经计算可得||fn||L≤16M0+lnln4,这样

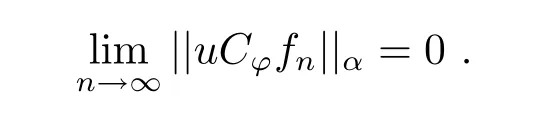
由文献[5]中引理2.3可得,对一切z∈D有

这表明(2.11)式成立.

另一方面,经计算且令z=zn并利用Pick引理及(2.11)式可得,当n→∞时,

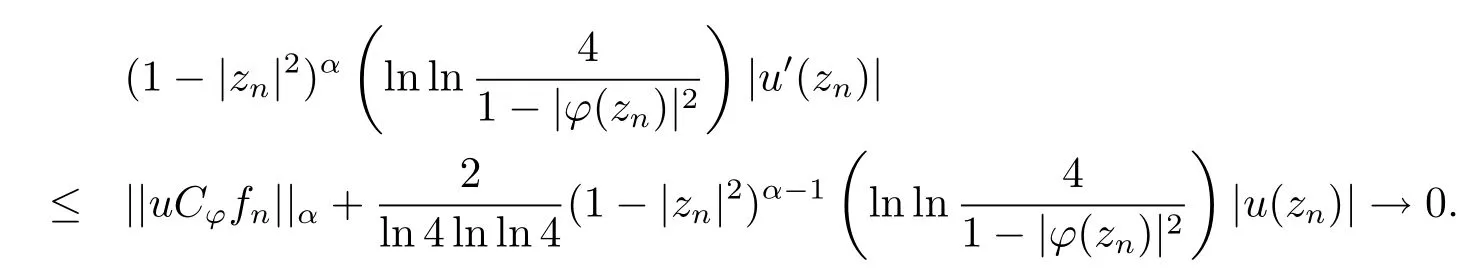
这表明(2.12)式成立.

反过来,若u∈βα,根据文献[5]中的引理2.3知(1-|z|2)α-1|u(z)|≤c||u||α,又由于φ∈H∞⊂β1,故(1-|z|2)|φ′(z)|≤||φ||1对一切z∈D成立.

设{fn}是βL中任一有界序列且在D的任一紧子集上一致收敛于0,则由Cauchy积分公式立即可得也在D的任一紧子集上一致收敛于0.当||φ||∞＜1时,若n→∞,则

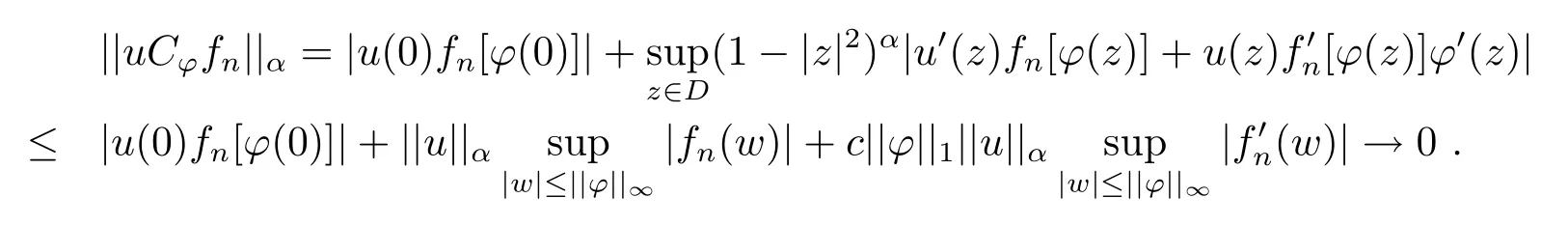
这意味着uCϕ是βL到βα的紧算子.

当||φ||∞=1时,若还有(2.11)–(2.12)式成立,故对任意ε＞0,存在0＜δ＜1,当δ＜|φ(z)|＜1时,

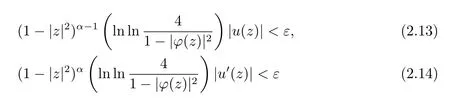
同时成立.

记K=sup||fn||L,则由文献[6]中的引理2.1、Pick引理以及(2.13)–(2.14)式可得

这样就有

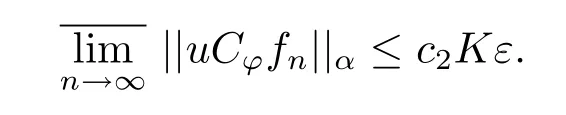
由ε的任意性知

这意味着uCϕ是βL到βα的紧算子.

[1]Madigan K,Matheson A.Compact composition operators on the Bloch Space[J].Trans.Amer. Math.Soc.,1995,347:2679–2687.

[2]Madigan K.Composition operators on analytic Lipschitz spaces[J].Pro.Amer.Math.Soc.,1993, 119(2):465–473.

[3]Shi J H,Luo L.Composition operators on the Bloch space of several complex variables[J].Acta. Math.Sin.(English Series),2000,16:85–98.

[4]Ohno S,Zhao R H.Weighted composition operators on the Bloch space[J].Bull.Austral.Math. Soc.,2001,63:177–185.

[5]张学军.p-Bloch空间上的复合算子和加权复合算子[J].数学年刊,2003,24A(6):711–720.

[6]叶善力.不同权的Bloch型空间之间的加权复合算子[J].数学学报,2007,50(4):927–942.

[7]Zhu K H.Spaces of holomorphic functions in the unit ball[M].New York:Springer-Verlag(GTM 226),2005.

[8]Rudin W.Function theory in the unit ball of Cn[M].New York:Springer-Verlag,1980.

[9]赵艳辉.单位球上F(p,q,s)空间到βL空间的加权Cesaro算子[J].数学杂志,2011,31(4):722–728.

CHARACTERIZATION OF WEIGHTED COMPOSITION OPERATORS BETWEEN DIFFERENT WEIGHTED BLOCH TYPE SPACES AGAIN

FAN Hai-xia,XI Li-hua,ZHANG Xue-jun
(College of Mathematics and Computer Science,Hunan Normal University,Changsha 410006,China)

In the paper,the authors discuss the conditions that the weighted composition operator uCφis a bounded operator or compact operator from the space βLto the space βαin the disc.By the way of order’s estimation,the briefly sufficient condition and necessary conditions are given,which extend Ye Shanli’s results.

boundedness;compactness;weighted composition operator;Bloch type space; unit disc

tion:30D45;47B38

O174.51;O177.2

A

0255-7797(2017)01-0169-08

2014-04-25接收日期:2015-02-11

湖南省自然科学基金资助(2015JJ2095).

范海霞(1989–),女,湖南衡阳,硕士,研究方向:函数空间和算子理论.