有限域上n元n次方程只有零解的充要条件

陈玺,屈龙江,李超,2

(1.国防科技大学理学院数学与系统科学系,湖南长沙410073)

(2.信息保障科学与技术实验室,北京100072)

有限域上n元n次方程只有零解的充要条件

陈玺1,屈龙江1,李超1,2

(1.国防科技大学理学院数学与系统科学系,湖南长沙410073)

(2.信息保障科学与技术实验室,北京100072)

本文研究了有限域上只有零解的n元n次方程的结构问题.利用对有限域上不可约多元多项式在其扩域中的分解特征的刻画,结合Chevalley定理,得到了有限域上n元n次方程只有零解的一个充要条件,并给出这类方程的一些新的具体构造.

有限域;方程只有零解;多元多项式分解;不可约多项式

1 引言

有限域上的多项式理论在编码密码、有限几何、组合设计等领域均有非常重要的应用,近年来得到了许多学者的关注和研究,详见文[1,2]及其中的参考文献.多元多项式方程解数的计算和估计是有限域上多项式理论的重要内容,在工程实际中应用广泛,如应用多项式理论构造密码系统、纠错码或者组合设计对象时,构造对象的参数计算问题往往可以转化为有限域上多项式方程解数的计算问题.然而,有限域上多元多项式方程的解的问题一直是困难的数学问题.Chevalley定理是该方面的一个重要结果:设f∈Fq[x1,···,xn]且满足f(0,···,0)=0,deg(f(x1,···,xn))＜n,则方程f(x1,···,xn)=0在Fq上有非平凡解,即存在

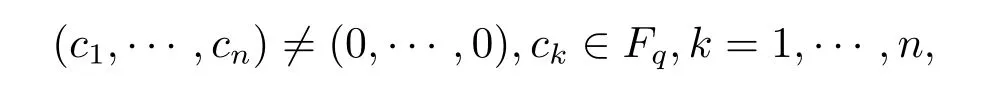
使得f(c1,···,cn)=0.但是当n=deg(f(x1,···,xn))时,上述结论并不成立.Dickson[3,4]给出了如下反例:设n∈Z+,{α1,···,αn}为Fqn在Fq上的一组基.令

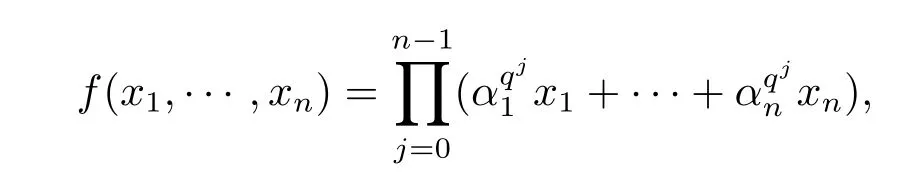
则f(x1,···,xn)为系数在Fq上的多项式,且方程f(x1,···,xn)=0在Fq上只有零解(0,···,0).该反例中的函数通常被称为具有范形式,一个自然的问题是:有限域上只有零解的n元n次方程应该具有什么样的特征呢?能否构造出更多这样的例子呢?Carlitz[5]证明了若q≥13,f∈Fq[x1,x2,x3]为一个齐三次多项式,且满足f在Fq上仅在(0,0,0)处为零,则f必然具有范形式.Terjanian[6]证明了若n次多项式f∈Fq[x1,···,xn]且在Fq上仅有零解,则对任意次数小于n的多项式g∈Fq[x1,···,xn],方程f(x1,···,xn)=g(x1,···,xn)在Fq上至少有一解.Carlitz[7],Felszeghy[8],Francis[9]等人先后给出了一些有限域上特殊的多元多项式方程的解的个数及解法.本文是对该问题的一个一般回答.首先给出了有限域上不可约多元多项式在其扩域中分解特性.在此基础上,结合Chevalley定理,得到了有限域上n元n次多项式方程f=0在Fq上只有零解的一个充要条件.该条件在f不是完全不可约的情形下,更为具体的描述了f必须具有范形式.

全文结构如下:第2节刻画了有限域上不可约多元多项式在其扩域中分解特征;第3节给出了有限域上n元n次多项式方程f=0在Fq上只有零解的充要条件,并给出了一些具体的构造实例;第4节总结并提出有待进一步研究的问题.

2 不可约多元多项式在其扩域中分解特征

为刻画有限域上不可约多元多项式在其扩域中分解特点,首先引进一些基本概念和相关性质.

定义1设f(x1,···,xn)=为有限域FqN上的n元多项式.令

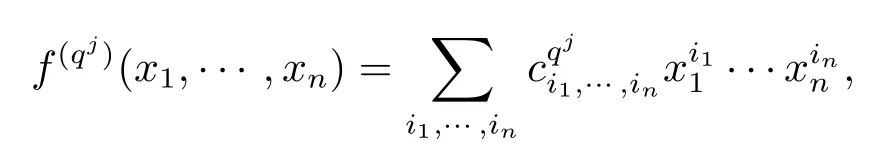
其中j≥0,即将多项式的每个系数都做qj次提升,称f(qj)(x1,···,xn)为f(x1,···,xn)的qj次提升.

由定义直接可得如下结论.

引理1(f1(x1,···,xn)f2(x1,···,xn))(q)=

引理2f(x1,···,xn)不可约当且仅当f(q)(x1,···,xn)不可约.

引理3设f(x1,···,xn)∈Fq[x1,···,xn],f1(x1,···,xn)∈FqN[x1,···,xn]且满足

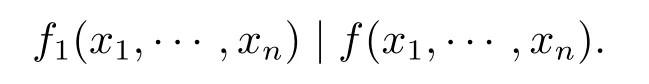
证设f(x1,···,xn)=f1(x1,···,xn)H(x1,···,xn),H(x1,···,xn)∈FqN[x1,···,xn].

于是,由引理1有

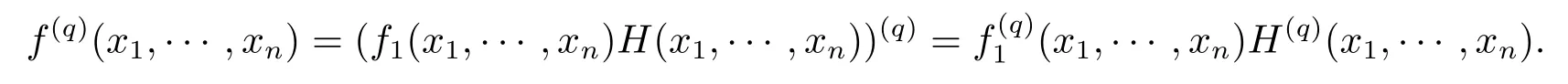
另一方面,由f(x1,···,xn)∈Fq[x1,···,xn]知f(x1,···,xn)=f(q)(x1,···,xn).结合两式,得进而对任意非负整数j(0≤j≤N-1),均有

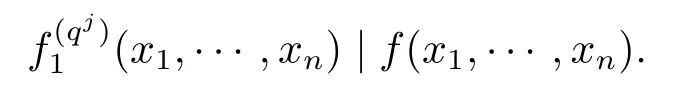
定理1设f(x1,···,xn)为Fq上n元M次不可约多项式,f1(x1,···,xn)为FqN上n元l次首一不可约多项式,且满足f1(x1,···,xn)|f(x1,···,xn).则有l|M,FqM/l为包含f1(x1,···,xn)系数的最小域,且

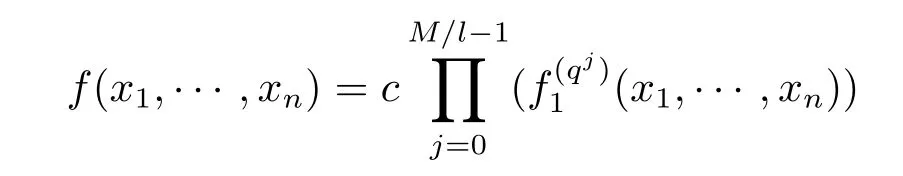
对某个c∈Fq成立.

证设t为使得=bf1(x1,···,xn)对某个b∈FqN成立的最小正整数.由f1(x1,···,xn)=知这样的t一定存在.又因为f1(x1,···,xn)是首一的,故b=1,即=f1(x1,···,xn).进一步,Fqt为包含f1(x1,···,xn)所有系数的最小域.

由引理2和f1(x1,···,xn)为FqN[x1,···,xn]中首一不可约多项式知,j=0,···,t-1均为FqN[x1,···,xn]中的首一不可约多项式,因此多项式

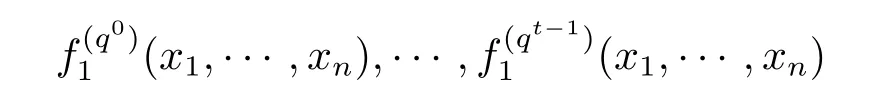
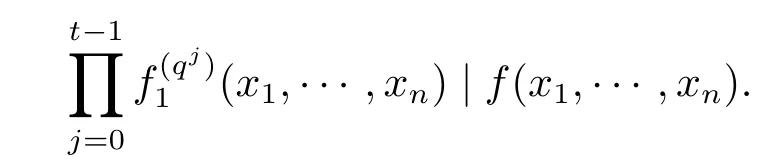
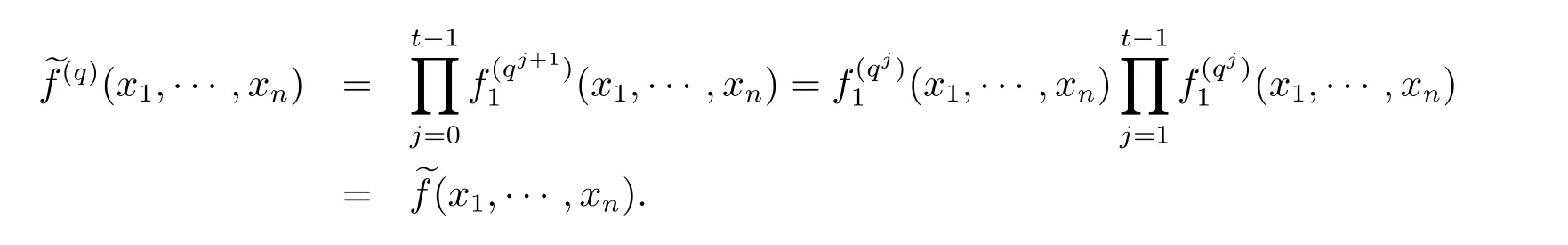
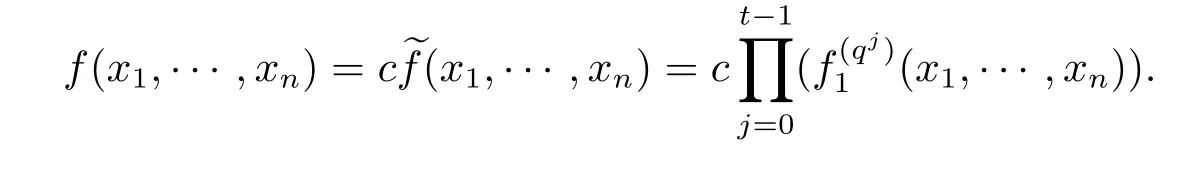
因此

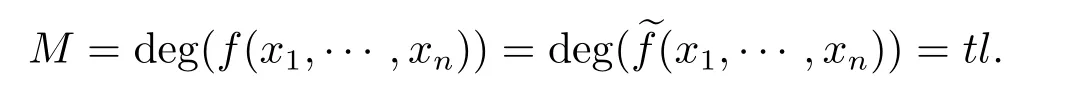
于是l|M,且t=M/l.由t的定义知,显然FqM/l为包含f1(x1,···,xn)系数的最小域.

3 主要结果

3.1 n元n次方程只有零解时的充要条件

引理4(见文[1,推论6.9])设f1(x1,···,xn),···,fm(x1,···,xn)∈Fq[x1,···,xn],对i=1,···,m,满足fi(0,···,0),且

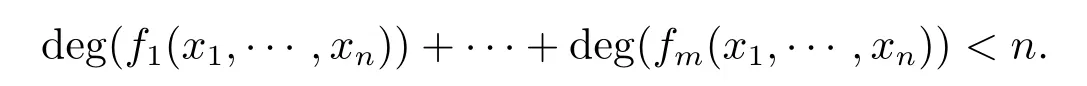
则存在(c1,···,cn)(0,···,0),ck∈Fq,k=1,···,n使得fi(c1,···,cn)=0对i= 1,···,m成立.

定理2设f(x1,···,xn)为Fq上n元n次多项式,则f(x1,···,xn)=0在Fq上只有零解当且仅当对n的某个正因子l,f可以表示为如下形式

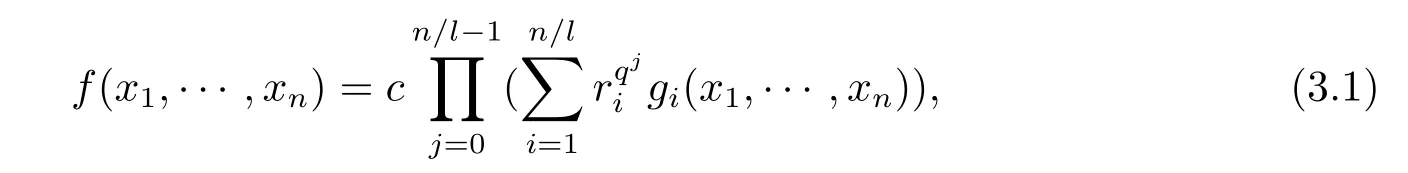
证(充分性)设f如(3.1)式表示.容易验证f(x1,···,xn)确为Fq上n元n次多项式.下面只需证f(x1,···,xn)=0在Fq上只有零解.设存在(c1,···,cn),其中ck∈Fq,k=1···n,使得f(c1,···,cn)=0.则由(3.1)式知,存在0≤r≤n/l-1,使得

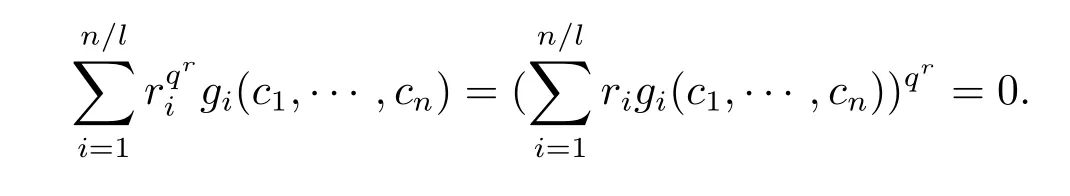
(必要性)设f(x1,···,xn)=0在Fq上只有零解,则由Chevalley定理知f(x1,···,xn)必在Fq上不可约.假若不然,设

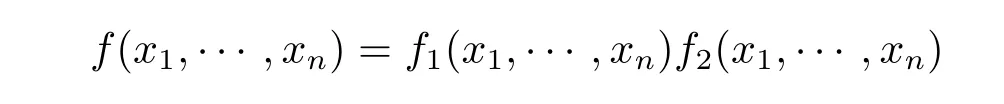
为f(x1,···,xn)在Fq上的一个非平凡分解,则有f1(0,···,0)=0或者f2(0,···,0)= 0.不妨设f1(0,···,0)=0.但由1≤degf1(x1,···,xn)≤n-1和Chevalley定理知f1(x1,···,xn)=0在Fq上必有非零解,从而f(x1,···,xn)=0在Fq上也有非零解,矛盾！从而f(x1,···,xn)必在Fq上不可约.

若f(x1,···,xn)完全不可约,即其在Fq的任何扩域上均不可约,则有l=n,令c=r1=1,g1=f.于是结论成立.

若f(x1,···,xn)不是完全不可约的,则存在Fq的某个扩域FqN上的l(1≤l＜n)次不可约多项式f1(x1,···,xn)满足f1(x1,···,xn)|f(x1,···,xn).由定理1得l|n,Fqn/l为包含f1(x1,···,xn)系数的最小域,且

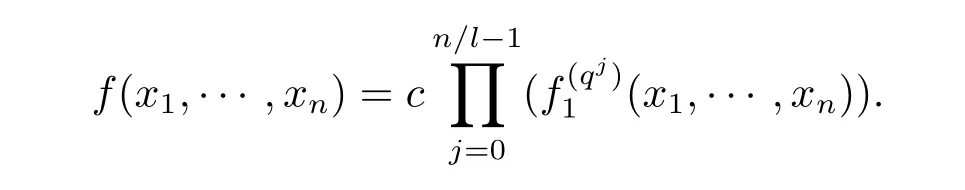
因为f1(x1,···,xn)是FqN上的l次多项式,所以存在r1,···,rm为Fqn/l中一组在Fq上线性无关的元素,g1(x1,···,xn),···,gm(x1,···,xn)为Fq上一组次数均不超过l的多项式,使

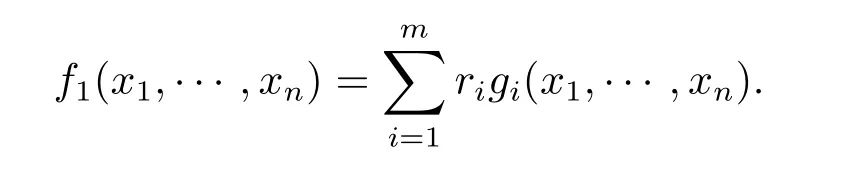
于是

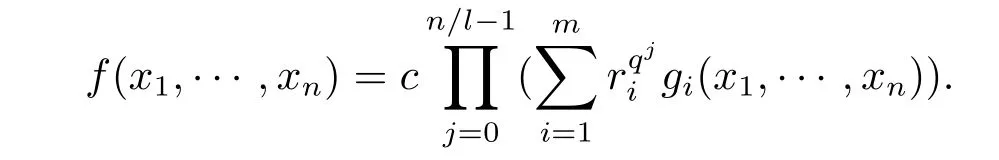
由f(x1,···,xn)=0在Fq上只有零解知f1(x1,···,xn)=0在Fq上只有零解,又因为r1,···,rm∈FqN在Fq上线性无关,所以方程组gi(x1,···,xn)=0,i=1,···,m在Fq上只有零解.

因为deg(gi(x1,···,xn))≤l,所以

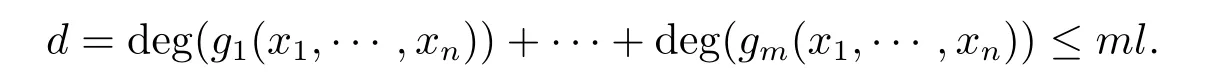
若d＜n,由引理4,方程组gi(x1,···,xn)=0,i=1,···,m在Fq上有非零解,矛盾！所以n≥d≥ml.

另一方面,由r1,···,rm∈Fqn/l在Fq上线性无关知n/l≥m.于是m=n/l,且等号当且仅当deg(g1(x1,···,xn))=···=deg(gm(x1,···,xn))=l时成立.

综上所述,此时

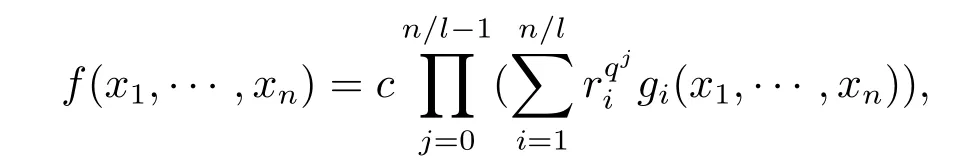
3.2 应用及举例

例1 F3上的4元4次多项式

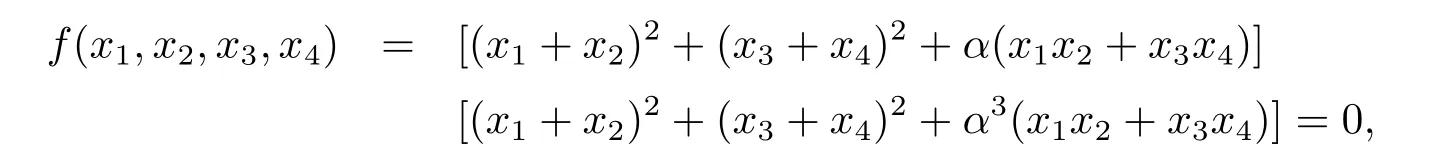
在F3上只有零解,其中α∈F32F3.

证显然f(x1,x2,x3,x4)是F3上的4元4次多项式.由于F32是F3的二次扩张, α∈F32F3,故1,α为F32在F3上的一组基.由定理2可得,f(x1,x2,x3,x4)=0在F3上只有零解当且仅当方程组

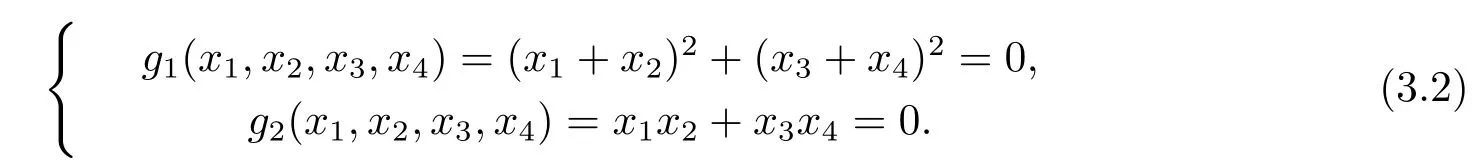
在F3上只有零解.注意到1是F3上的非平方元,g1=0当且仅当x1=-x2且x3=-x4,代入g2=0得-=0,从而x1=x3=0.进一步,x2=x4=0,即f(x1,x2,x3,x4)=0在F3上只有零解.

推论1设n为正整数,l为n的某个正因子,x1,···,xn为n个不同的变元,xi1,···,xil, 0≤i≤n/l-1为变元x1,···,xn的一个分划.设

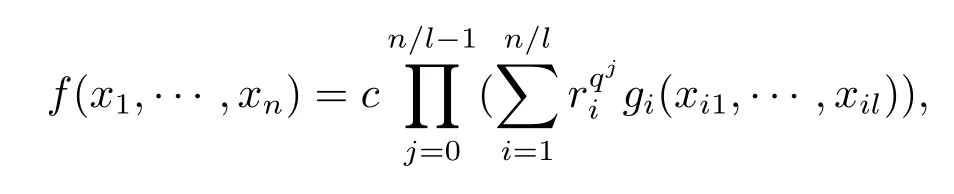
证因为每个方程gi(xi1,···,xil)=0,i=1···n/l限制在自身l个变元上时,在Fq上只有零解,所以方程组gi(x1,···,xn)=0,i=1···n/l在Fq上只有零解.由定理2,命题成立.

在上述推论中,令l=1;对i=1,···,n/l=n令gi(xi)=xi,则得到前文Dickson的实例.

在推论1中,每个方程gi(xi1,···,xil)=0,i=1···n/l限制在自身l个变元上时,可以看做l元l次多项式

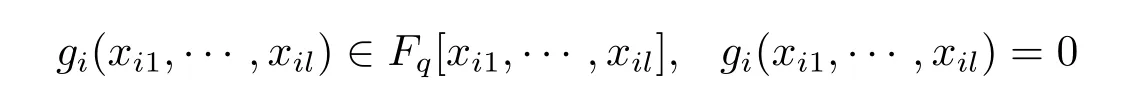
在Fq上只有零解.这表明可以用任意m个在Fq上只有零解的l元l次多项式,构造出在Fq上只有零解的ml元ml次多项式.下面是一个具体的例子.

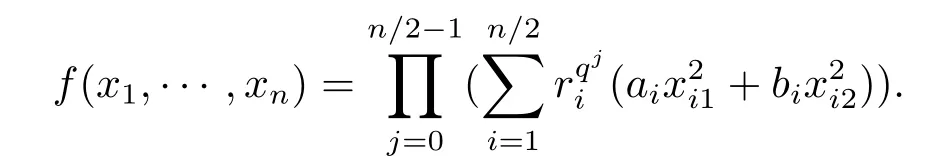
则n元n次方程f=0在Fq上只有零解.

注意到例2中的f没有交叉项,利用反证法容易证明f不含一次因式,因此是与Dickson实例不同构的只有零解的n元n次方程.例2利用n/2个限制在自身两个变元上在Fq上只有零解的2次方程,构造出了高次的只有零解的方程.

从定理2的证明可以看出,若f(x1,···,xn)完全不可约,则得到对应定理2的l=n的平凡情形.但对于给定的有限域Fq和正整数n,这种平凡情形可能发生,也可能不能发生.如文[5]中表明对于给定有限域Fq,q≥13和正整数n=3,l=3时,定理2中的平凡情形是不存在的.

例3设F3上的4元4次多项式

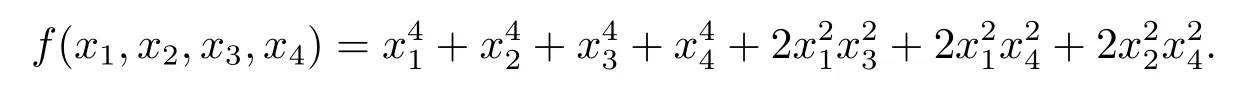
容易验证f(x1,x2,x3,x4)在F3上只有零解,且其在F3的任何扩域上均不可约.此时对应定理2中l=n的平凡情形.

4 总结与展望

本文首先刻画了有限域上不可约多元多项式在其扩域中分解特征,然后结合Chevalley定理,得到了有限域上n元n次多项式方程f=0在Fq上只有零解的充要条件,并进一步构造了一些具体实例.该条件在f不是完全不可约的情形下,更为具体的描述了f必须具有范形式.进一步也可以考虑给出更多具体的例子.例3表明了当f完全不可约时,定理2是平凡的,因此如何刻画有限域上完全不可约的n元n次方程只有零解的条件依旧是一个值得研究的方向.

[1]Lidl R,Niederreiter H.Finite fields[M].Cambridge:Cambridge University Press,1997.

[2]Gary L Mullen,Daniel Panario.Handbook of finite fields[M].Boca Raton:CRC Press,2013.

[3]Dickson L E.On triple algebras and ternary cubic forms[J].Bulletin of the American Math.Soc., 1908,14(4):160–169.

[4]Dickson L E.On the representation of numbers by modular forms[J].Bulletin of the American Math. Soc.,1909,15(7):338–347.

[5]Carlitz L.A theorem of Dickson on nonvanishing cubic forms in a finite field[J].Proc.American Math.Soc.,1957,8(5):975–977.

[6]Terjanian,Guy.Sur les corps finis[J].C.R.Acad.Sci.Paris Sr.,1966,262:A167–A169.

[7]Carlitz L.Solvability of certain equations in a finite field[J].Acta Arith.,1961,7:389–397.

[9]Francis N Castro.On systems of linear and diagonal equation of degree pi+1 over finite fields of characteristic p[J].Finite Fields Appl.,2008,14(3):648–657.

THE STRUCTURE OF THE EQUATION OVER FINITE FIELDS WITH n UNKNOWNS AND WITH DEGREE n WHICH VANISH ONLY AT ZERO

CHEN Xi1,QU Long-jiang1,LI Chao1,2
(1.Departement of Mathematics and System Science,National University of Defense Technology, Changsha 410073,China)
(2.Information Assurance Science and Technology Laboratory,Beijing 100072,China)

In this paper,we investigate the structure of the equation over finite fields with n unknowns and with degree n which vanish only at zero.By using the factorization of the irreducible multivariable polynomial in some extension field and with the Chevalley Theorem, a sufficient and necessary condition of the equation with n unknowns and with degree n which vanish only at zero is obtained.Furthermore,we construct some explicit equations of this class.

finite field;equation which vanish only at zero;multivariate polynomial factorization;irreducible polynomial

tion:12E12;12E20

O153.4

A

0255-7797(2017)01-0138-07

2014-03-25接收日期:2014-09-09

国家自然科学基金资助(61272484);信息保障科学技术实验室开放基金资助(KJ-12-02).

陈玺(1990–),男,辽宁大连,硕士,主要研究方向:编码密码理论及其应用.