向量范数的积分不等式与应用
沈进中, 邓留保
(1.安徽理工大学电气与信息工程学院,安徽淮南232001; 2.安徽财经大学金融学院,安徽蚌埠233030)
向量范数的积分不等式与应用
沈进中1, 邓留保2
(1.安徽理工大学电气与信息工程学院,安徽淮南232001; 2.安徽财经大学金融学院,安徽蚌埠233030)
证明了2-范数积分不等式,进一步将其推广到一般范数的积分不等式.作为该结果的一个应用,本文在最后一部分给出一个实例说明采用一般的向量范数也可以证明微分方程解的唯一性,从而扩展了微分方程理论分析的思维方法.
向量范数; 积分不等式; Lebesgue零测度集; 非自治系统
1 引 言
常微分方程理论不仅广泛应用于工业,农业,生物工程,航空航天,系统工程等领域,而且是系统理论研究的重要工具.在涉及向量长度时,文献[1-2]中采用的是2-范数.当前,几乎所有的常微分方程专著[3-5]的理论分析中都是采用1-范数[6],而没有采用其他的向量范数或矩阵范数,这是笔者在学习常微分方程时一直存在的一个疑问.一般而言,最能直观体现一个n维向量的长度的范数是2-范数,即是欧氏范数.笔者曾尝在解的存在性和唯一性证明过程中用2-范数代替1-范数,但是发现一个最大的问题就是无法得到一个范数积分不等式,带着这个问题,经过深入研究,最终解决此问题,并将结果作了进一步推广.
2 预备知识
P-范数:x=(x1,x2,…xn)∈n, ‖∞.
1-范数:x=(x1,x2,…xn)∈n, ‖
2-范数:x=(x1,x2,…xn)∈n, ‖
引理1[7]复数值函数w(t)=u(t)+iv(t)在[a,b]上可积,则成立

引理2[6]有限维线性空间上的不同范数等价.
3 主要结果
定理3.1单变量向量值函数x(t)=(x1(t),x2(t),…xn(t))∈n,若对每个分量xi(t)均在[a,b]可积,则
(1)
证采用数学归纳法.
当n=1时, x(t)=x1(t)∈1,根据定积分不等式,显然结论(1)成立.
当n=2时,根据引理1可知,结论(1)成立.
假设n=k时,结论(1)成立,即
(2)
那么,若x(t)=(x1(t),x2(t),…xk+1(t))∈k+1每个分量xi(t)均在[a,b]可积,根据黎曼可积的充要条件,则在[a,b]可积.应用引理1,有

化简,得

(3)
再根据假设条件(2)式,有
(4)
应用(3)和(4),立即可得
(5)
即

注3.1 定理3.1表明当向量的范数取为2-范数时,积分不等式(1)成立.在文献[4-7]中的向量范数是1-范数,此范数结构简单,易于验证积分不等式
成立,但1-范数缺点是对点的长度刻画不够直观.既然1-范数和2-范数都满足积分不等式,是否所有的向量范数都满足积分不等式呢?这个难以回答,究其原因,范数实质是一个定义在线性空间上的,且满足非负性、齐次性、三件不等式的任何一个实数值函数,可见范数的形式有无穷多个.没有具体的范数表达式去分析就会显得比较困难,这里给出一个弱一点的结果.
定理3.2设‖·‖a是Rn中向量范数,则存在常数c>0使得
(6)
其中x(t)=(x1(t),x2(t),…xn(t))∈n,且对每个分量xi(t)均在[a,b]可积.
证首先需说明的是,‖x(t)‖a在[a,b]上可积.根据范数满足三角不等式,有
‖x(t+Δt)-x(t)‖a≤ |x1(t+Δt)-x1(t)|·‖e1‖a+…+|x1(t+Δt)-x1(t)|·‖en‖a,


再根据定理3.1的结论,得
这就证明了定理3.2.
注3.2 从定理3.2可以看出,定理3.1是定理3.2的中c=1时的特例.
对于P-范数,是否有类似于(1)式的积分不等式呢?这里给出一个充分条件
定理3.3正常数p≥1,若对于在[a,b]上可积任意实函数x(t),y(t),总成立
则
其中‖·‖p为P-范数,x(t)=(x1(t),x2(t),…xn(t))∈n且每个分量xi(t)均在[a,b]可积.
证采用数学归纳法,仿照定理3.1的证明过程,完成是容易的,不再赘述.
4 应 用
用结论2来证明非自治微分方程解的唯一性.一个非自治微分方程(非自治系统)初值问题可以描述为
(7)
命题4.1若非自治微分方程(7)有唯一解,且满足Lipschitz条件,则解是唯一的.
证任取一种n中向量范数‖·‖a.设(7)有两个解φ(t),φ(t),则

由于φ(t),φ(t) 在t∈I上连续,因此
‖φ(s)-φ(s)‖a≤A, ∀t∈I.
(8)
根据Lipschitz条件, 有
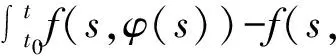
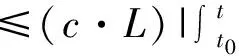
(9)
如此下去,采用数学归纳法,容易得到
(10)
其中m为任意正整数,从(10)式右端可知‖φ(s)-φ(s)‖a=0,即得φ(s)=φ(s).
注意上述证明过程有一些细节并未说明,而是默认其成立,但证明的思路是正确的.之所以这么做,主要是说明在微分方程解的唯一性定理证明过程中是可以采用任意一种向量范数的,而不仅仅是1-范数,因此没有在细节上考究,毕竟证明的思想在许多文献中都有[2-5].
5 结 语
本文主要研究了2-范数积分不等式,并给出了严格数学证明.然后对一般的范数的积分不等式也做出了证明,分别以定理3.1和定理3.2的形式给出,并对P-范数的积分不等式成立给出了一个充分条件,事实上也是必要条件.这些结果在常用的常微分方程参考书中暂未发现[2-5,9].在本文第4部分举出了一个例子说明在证明唯一性的过程中,选取的范数可以是任何一个向量范数.本文结果可以扩大分析问题的思维方式.值得注意的是定理3.2中的(6)式里面的常数c是否等于1上不知道,这需要进一步的研究.
[1] 邬弘毅,潘卫,王春生.有关解线性方程组的一些思考[J].大学数学, 2010,26(6): 174-177.
[2] 刘莉,王伟.矩阵方程AXAT+BYBT=C的双对称最小二乘解及其最佳逼近[J].大学数学, 2012, 28(6): 67-73.
[3] 丁同仁,李承治.常微分方程教程[M].北京:高等教育出版社,2004,170-171.
[4] 王高雄,周之铭,朱思铭,等.常微分方程[M].3版.北京:高等教育出版社, 2006,195-196.
[5] 袁荣.常微分方程[M].北京:高等教育出版社,2012,161-170.
[6] 方保镕,周继东,李医民.矩阵论[M].北京: 清华大学出版社,2004:160-170.
[7] Brown J W,Churchill R V, Lapidus M.Complex variables and applications[M].New York: McGraw-Hill,1996.
[8] 徐森林,薛春华.实变函数论[M].北京: 清华大学出版社,2009.
[9] 楼红卫,林伟.常微分方程[M].上海: 复旦大学出版社,2007.
The Integral Inequality of Vector Norms and its Application
SHENJin-zhong1,DENGLiu-bao2
(1.College of Electrical and Information Engineering, Anhui University of Science and Technology, Huainan Anhui 232001, China;2.School of Finance, Anhui University of Financial and Economics, Bengbu Anhui 233030, China)
This paper proves the integral inequality of 2-norm, furthermore, this result is extended to common vector norms.As an application,there is an example to illustrate the uniqueness of the solution of the differential equation can be proved by applying a common vector norm in the last part, which can extend more thoughts in theoretical analysis of ordinary differential equation.
vector norms; integral inequality; set of Lebesgue measure zero; nonautonomous system
2016-07-12; [修改日期]2016-09-30
安徽理工大学硕博基金(ZY022);安徽高校自然科学研究重点项目(KJ2015A076)
沈进中(1985-),男,博士,讲师,从事非线性系统研究.Email:jzshen009@163.com
O172.2
C
1672-1454(2016)06-0083-04

