L2,1范数正则化的广义核判别分析及其人脸识别*

傅俊鹏，陈秀宏，葛骁倩

江南大学 数字媒体学院，江苏 无锡 214122

L2,1范数正则化的广义核判别分析及其人脸识别*

傅俊鹏+，陈秀宏，葛骁倩

江南大学 数字媒体学院，江苏 无锡 214122

FU Junpeng,CHEN Xiuhong,GE Xiaoqian.Face recognition by generalized kernel discriminant analysis viaL2,1-norm regularization.Journal of Frontiers of Computer Science and Technology,2017,11(1)：124-133.

特征选取和子空间学习是人脸识别的关键问题。为更准确选取人脸中丰富的非线性特征，并解决小样本问题，提出了一种新的L2,1范数正则化的广义核判别分析（generalized kernel discriminant analysis based onL2,1-norm regularization，L21GKDA）。利用核函数将原始样本隐式地映射到高维特征空间中，得到广义核Fisher鉴别准则，再利用一种有效变换将该非线性模型转化为线性回归模型；为了能使特征选取和子空间学习同时进行，在模型中加入了一种L2,1范数惩罚项，并给出该正则化方法的求解算法。因为方法借助于L2,1范数惩罚项的特征选取能力，所以它能有效地提高识别率。在ORL、AR和PIE人脸库上的实验结果表明，新算法能有效选取人脸的非线性特征，提高判别能力。

人脸识别；特征选取；子空间学习；L2,1范数；核判别分析

1 引言

近几十年来，人脸识别技术得到了很大的发展，子空间学习是人脸识别中的关键步骤，其中最具代表性的无监督算法和有监督算法分别为主成分分析（principal component analysis，PCA）[1]和线性判别分析（linear discriminant analysis，LDA）[2]。

3.由于招标代理机构对有关政策规定把握不住，业务能力不强引起的不规范行为。一是招标采购文件存在以不合理的条件对供应商实行差别待遇或者歧视待遇条款。二是采购文件未体现政府采购促进中小微企业发展之政策。三是采购公告内容信息不完整。四是采用综合评分法时评审标准中的分值未与评审因素的量化指标相对应。五是采购需求中的技术要求指向特定产品。六是采购文件将非进口投标产品生产厂家授权函原件及售后服务承诺函原件作为资格条件。

PCA以重构为目的，将训练样本投影到低维的子空间中，使投影后样本的方差最大，最大程度地去除噪声和冗余，达到降维的目的。LDA以分类为目的，基于Fisher准则寻找一组最佳鉴别矢量，将高维样本投影到低维空间中，使投影后样本的类内离散度趋于最小，而类间离散度趋于最大。对于人脸识别问题，LDA方法更为有效。然而，Fisher准则经常会遇到小样本问题[2]，即训练样本过少，导致类内离散度矩阵奇异。

为更准确选取特征，并解决小样本问题，许多LDA相关的方法被提出。这些方法大致分为两类：特征选取和子空间学习。特征选取，指的是在样本的原始特征中选取一组最具代表性或者区分度的特征。子空间学习，指的是通过学习得到投影矩阵，将高维数据投影到低维子空间中。子空间学习中较具代表性的有主成分分析[1]、线性判别分析[2]、局部保持投影（locality preserving projections，LPP）[3]、不相关判别分析（uncorrelated linear discriminant analysis，ULDA）[4-5]等。然而，上述方法得到的低维特征是基于所有原始特征的，未能区分各个特征的重要程度。因此，一些稀疏子空间学习算法被提出来，如稀疏判别分析（sparse discriminant analysis，SDA）[6]、稀疏张量判别分析（sparse tensor discriminant analysis， STDA）[7]和稀疏主成分分析（sparse principal component analysis，SPCA）[8]等。然而，这些稀疏子空间学习算法，其子空间的各个维度所选取的特征均不相同。

假设一投影矩阵，它的每一行对应着选取样本某一特征的权重，每一列为子空间的一个基底。将样本投影到该子空间，希望抛弃原始样本中无用的特征，保留重要的特征。由此，需要算法能学习到一个行稀疏的投影矩阵，把这些无用的特征对应的权重置为0，使特征选取和子空间学习同时进行。

信息化管理是以信息化带动业务产业链上的每一个工作流程，通过信息技术的引进管理，实现企业管理现代化的过程，有利于重新整合企业内外部资源，提高企业效率和效益、增强企业竞争力的过程，对于周转材料租赁业务，有利于集中管理优势，主要体现在以下几点。

考虑到在人脸识别问题中，由于表情、姿态、光照等的变化，导致人脸图像分布是非线性的，因此线性算法在进行人脸等图像识别时，通常不能取得令人满意的效果。Mika等人[13]利用核方法将LDA扩展到了非线性的情况，提出了核判别分析（kernel discriminant analysis，KDA）。随后，Yang[14]又提出了Kernel Eigenfaces和Kernel Fisherfaces，然而KDA同样面临着小样本问题。

基于上述问题的启发，考虑到联合特征选取和子空间学习方法以及核技术的优越性，提出了一种新的L2,1范数正则化的广义核判别分析（generalized kernel discriminant analysis based onL2,1-norm regularization，L21GKDA)。该方法首先利用核函数将样本映射到高维特征空间中，将求解广义核Fisher鉴别准则的问题转化为求解线性回归的问题；再加入L2,1范数惩罚项，并对该优化问题进行求解，从而在高维特征空间中进行联合特征选取和子空间学习，同时也解决了小样本问题。最后在ORL、AR和PIE人脸库上进行实验，验证了算法的有效性。

2 核判别分析

3 L2,1范数正则化的广义核判别分析

对于矩阵A∈RN×(C-1)，将样本投影到C-1维的子空间中。若将它的第i行、第j列分别记为ai和aj，则它的L2,1范数定义为，即所有行向量的二范数之和。

假设非线性映射φ:x→φ(x)将样本映射到高维空间，并得到核矩阵K=φ(X)Tφ(X)，是一个半正定对称矩阵。基于广义核Fisher鉴别准则函数[15]，经推导可得：

其中，E=diag(E1,E2,…,EC)∈RN×N，是一个块对角矩阵。矩阵中的所有元素值为1/Ni。

2.3 虫种变化 原清远县历史为以间日疟为主、恶性疟和三日疟高度混合流行［1］。20世纪90年代流行虫种间日疟占99.60%（2 250/2 259），恶性疟占0.13%（3/2 259），其他占0.27%（6/2 259）；2006年以来共报告输入病例13例，其中恶性疟占69.23%（9/13）、间日疟占23.08%（3/13）、其他占7.69（1/13）。

令y=Ka，有：

那么使J(a)最大化的问题可转化为，先求使J(y)最大化的一组最佳鉴别矢量，再通过y=Ka求解a。对J(y)按变量y求导并使之为0得：

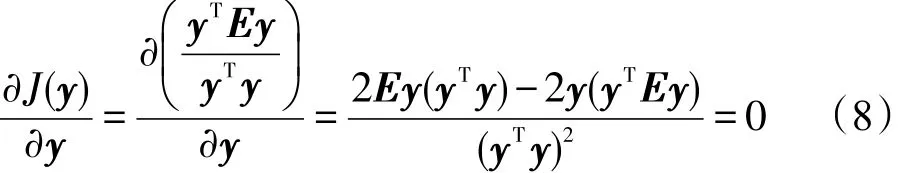
进而得到：

令J(y)=λ，则：

[6]Clemmensen L,Hastie T,Witten D,et al.Sparse discriminant analysis[J].Technometrics,2011,53(4):406-413.

船舶仪表设备在安装中通常应用橡胶减振器进行安装操作，具体分析主要的应用原因为：橡胶减振器在应用弹性模量较之金属减振器较小，可在较大的振动力下保持稳定，有利于保障设备运行中的安全稳定性。仪表设备在应用中其控制船舶的动力装置，因此对于仪表装置的稳定性要求较高。一般情况下在实际落实仪表设备安装中，主要通过安装固定模块，以及结合橡胶减振器的方式进行安装应用，以此保障设备安装应用质量的合格性，并且提升设备的实际应用效果。

其中，d=1,2,…,C。

由于1是E的重复特征值，需要在yd所限定的空间内，提取另外C个相互正交的向量作为特征向量。很明显，e=[1,1,…,1]T∈RN处在该空间内，可令e作为E的第一个特征向量，对剩下的特征向量进行斯密特正交化，使它们两两正交，最后移除e，得到C-1个特征向量，表示为：

求得向量组Y=[y1,y2,…,yC-1]后，接下来就是求解投影矩阵A=[a1,a2,…,aC-1]。然而，K是一个半正定对称矩阵，可能是奇异的，即小样本问题。为解决该问题，对于方程Y=KA，通常用最小二乘法来求解：

同时，为提高系统鲁棒性，常用的一种方法是加入惩罚项（正则化），对模型参数添加先验信息进行约束，使最终的解倾向于符合先验知识。那么对式（13）加入惩罚项μΩ(A)，其中μ为正则化参数，则该优化问题变为：

通常，的部分元素（也就是特征）和yd没有关系或不提供特征信息。将样本投影到子空间的表达式为KA，为了特征选取，A中某些行的所有元素应尽可能约等于0（即行稀疏），以便投影后去除样本中无用的特征；同时为了降维，需要选取一组最具判别性的基（最佳鉴别矢量），即同时进行特征选取和子空间学习。

加入L2,1范数惩罚项能够实现投影矩阵行稀疏，使其具有特征组选取能力。因为矩阵的L2,1范数是其所有行向量的二范数之和，最小化目标函数，能使投影矩阵行稀疏，即使解倾向于符合先验知识，满足特征选取与子空间学习同时进行的需求。

将式（14）中的Ω(A)替换为||A||2,1，得：

2011年3月，《中共贵州省委 贵州省人民政府关于加快水利改革发展的意见》（黔党发 〔2011〕2 号）提出：从土地出让收益中提取12%用于农田水利建设，省级统筹比例为20%，合理调整水资源费征收标准，扩大征收范围，水利建设基金征收年限延长到2020年，力争今后10年全社会水利投入年平均比2010年高出一倍。

对上式求关于A的偏导数，且令它为0得：

其中，G是一个对角矩阵，它的对角元素为：

当gii=0时，矩阵G奇异，此时可对gii增加一个小的扰动ε使之非奇异。

为了便于求解，应用Woodbury公式将式（16）表示为：

为了能直观地给出特征选取的作用，图3分别选取了L21GKDA、KDA和SDA算法得到的部分投影矩阵。其中列为子空间的基，即子空间的一个维度；行对应着选取特征的权重，即特征选取。

综上所述，求解该问题的算法表述如下：

算法1L21GKDA算法

4 实验与结果分析

为了验证L21GKDA算法的有效性，分别在ORL、AR和PIE人脸库上进行仿真实验，并将其结果与KDA[13]、SDA[6]及Fisherfaces[2]进行比较。此外，为了便于说明L21GKDA算法的优越性，也将其与L21FLDA算法[12]的实验结果进行比较。实验中将L21GKDA和L21FLDA的最大迭代次数设为50。算法中的核函数均采用多项式核函数k(x,x′)=(xTx′+1)b，此处的x,x′∈X，为使效果最佳，通过实验验证，将参数b取为2。Fisherfaces在PCA预降维阶段将类内离散度矩阵降到N-C维，而当N-C大于样本维数时则不采用PCA进行预降维。本文所有实验均独立随机地进行50次，采用最近欧氏距离分类器进行分类，计算其人脸识别率，取平均值。运行环境为Windows 7，Pentium®Dual-Core E6700 3.20 GHz CPU，内存为2 GB，编程环境为Matlab R2012b，以识别率作为主要的性能评价标准。

4.1 人脸库

（1）ORL人脸库（http://www.cl.cam.ac.uk/research/dtg/ attarchive/facedatabase.html），包含了40人的400幅面部图像，每人10幅。图像均在不同时间拍摄，人的面部细节和表情有不同程度的变化（如戴不戴眼镜、眼睛的睁闭、笑或严肃等)；人脸尺度最高可达10%的变化；人脸的姿态也有很大的变化，平面旋转或深度旋转最高可达20°。

（2）AR人脸库[16]，采集了126人的4 000多幅人脸图像。这些图像分两次采集（间隔两周以上），包含了人脸正面不同表情、不同光照和不同遮挡等变化。在本文的实验中，使用了其中120人的图像，每人26张，共3 120张。

（3）PIE人脸库[17]，包含了68人的41 368幅不同光照、表情、姿态下的图像。从中选取了包括光照、表情、姿态变化的5个子集（C05，C07，C09，C27，C29）的正面人脸图像共68人，每人170幅。

实验中，所有图像均压缩成32×32大小的灰度图，将其每列相连构成大小为1 024维的向量，并做归一化处理。3种人脸库的示例图像如图1所示。

Fig.1 Samples from ORL,AR and PIE face databases图1 ORL、AR、PIE人脸库的示例图像

4.2 实验结果

4.2.1 正则化参数μ对实验的影响

为研究联合特征选取和子空间学习中正则化参数μ对L21GKDA算法识别性能的影响，分别在3个人脸库上进行实验，并用L21FLDA算法作为对比。其中在ORL人脸库上每人随机取5幅图像作为训练样本，AR人脸库上每人取9幅，PIE人脸库上每人取20幅，余下图像作为测试，特征维数均保留C-1维（识别性能最佳的特征维数一般为C-1）。实验得到的平均识别率与正则化参数μ的关系如图2所示。

从图2可知，L21GKDA算法的识别率在大多情况下均高于L21FLDA，且效果更稳定。当μ=0时，识别率并不是最高的，随着正则化参数μ的增加，识别率有不同程度的增加。当μ=0.01时，从总体上看，两种算法的识别率达到最高，然后开始下降。这是因为，μ用于控制投影矩阵行稀疏的程度，取到合适的值时，能有效选取特征，提高识别率。而μ取值过大，矩阵会过于稀疏，对应于联合特征选取和子空间学习方法所选取到的特征过少，抛弃了部分对分类有用的特征，导致识别率下降。为更好地比较算法性能，以下实验均取μ=0.01。

Fig.2 Relationship between average recognition accuracy andμ图2 平均识别率与正则化参数μ的关系图

Fig.3 Examples of projection matrixes learned by L21GKDA,KDAand SDA图3 L21GKDA、KDA和SDA的投影矩阵实例图

4.2.2 特征选取的作用

叶建春：2011年，太湖局将贯彻落实中央1号文件、中央水利工作会议精神作为工作重点，按照水利部的部署，制定并印发了《太湖局贯彻落实中央1号文件任务分工实施方案》，提出了加强河湖管理、依法履职的各项举措，明确了加快推进流域水利改革发展的目标任务、质量要求和时间节点，并把实施方案作为开展流域水利工作的重要依据。2011年流域水利工作成效显著，为《条例》实施创造了有利局面。

其中，I为单位矩阵。

（7）利用好所有现有的自然景观，按照公路美学以及和周围自然环境相协调的原则进行设计，保证公路能够和自然环境融为一体。

当巷道达到极限平衡时，滑移面GF与水平线的夹角是(45°+φ/2)，滑动面EF与水平线的夹角是(45°-φ/2)，φ为松散岩体的折算摩擦角，φ=arctan (σc/10)，其中：σc为岩体的单轴抗压强度。五阳煤矿巷道底板煤层强度9 MPa，得出φ=40.1°。

从图3可知，图（a）第3、4行的权重约等于0（该两行的其他元素在完整的矩阵中也约等于0）。将样本投影到该子空间的表达式为KA，那么样本的第3、4两个特征没有被选取，即这两个特征自动被丢弃。而图（b）得到的低维特征是基于所有原始特征的，没有进行特征选取。图（c）完整的投影矩阵中，每行的元素并不全为0，各个维度上所选取的特征均不相同，未能区分样本的哪些特征应该选取，哪些特征该丢弃，实际应用中不一定能达到理想效果。由此可见，加入L2,1范数惩罚项能使特征选取和子空间学习同时进行，自动选取有用的特征，从而提高识别性能。

4.2.3 算法的收敛性实验及分析

为研究L21GKDA算法的收敛性，在ORL、AR和PIE人脸库上进行实验，并与L21FLDA算法进行对比。实验在ORL人脸库上每人随机取5幅图像作为训练样本，AR人脸库上每人取9幅，PIE人脸库上每人取20幅，研究目标函数式（15）的值与迭代次数的关系，实验结果如图4所示。其中，横坐标表示迭代次数，纵坐标表示目标函数的值。为了便于比较，图中目标函数的值已进行了归一化处理。最大迭代次数设为50。

由图4可知，得益于联合特征选取和子空间学习方法的收敛性[10]，两种算法均能快速地收敛到均衡点。图中也可以看出，L21GKDA算法的收敛速度快于L21FLDA，这是因为L21GKDA应用了核方法，将数据映射到新的特征空间，数据在该高维空间中的分布更加规则，使算法收敛更快。某种程度上也体现了L21GKDA算法的效率比L21FLDA的高。当迭代次数大于10时，目标函数的值在图中趋于平稳，已不再有明显的变化。

本节通过实验讨论训练样本数对识别率的影响。在ORL人脸库中，每人随机选取3、4、5、6、7幅图像进行训练；在AR人脸库中，每人随机选取3、6、9、12、15幅图像进行训练；在PIE人脸库中，每人随机选取5、10、20、30、40幅图像进行训练。特征维数均保留C-1维，余下的图像作为测试样本。表2～表4给出了3个人脸库上的平均识别率、标准差以及计算最佳鉴别矢量集所消耗的时间。

实验计算最近两次迭代中，两个目标函数值的差值，若该差值的绝对值小于0.01，则判定为收敛，结束迭代，并记录迭代次数。表1给出了不同人脸库中算法迭代次数的均值。

由表1可知，L21GKDA算法的平均迭代次数要少于L21FLDA算法，L21GKDA算法的收敛速度更快。另外，从实验中观察到，实验在同一人脸库不同训练样本数时，算法的迭代次数差异不大。也就是说，表中的平均迭代次数能基本反映算法的收敛速度，即L21GKDA算法收敛速度比L21FLDA的快，进一步反映了L21GKDA算法的优越性。

Table 1 Average number of iterations表1 平均迭代次数

4.2.4 训练样本数对实验的影响

为更全面地分析算法的收敛性，在每种人脸库上取5种不同的训练样本数进行实验。每次实验均独立随机地进行50次。

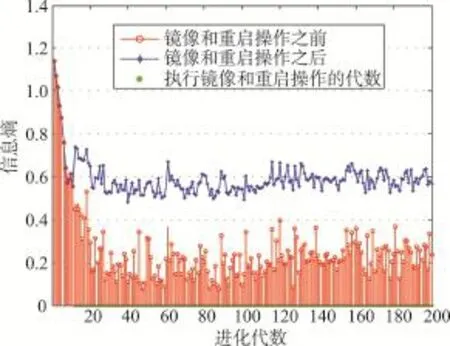
Fig.4 Relationship between the value of object function and iteration number图4 目标函数的值与迭代次数的关系图

从表2～表4可以看出，总体上看，L21GKDA算法的识别率最高且整体上相对稳定。基于L2,1范数正则化方法的识别率优于对应的未正则化方法，因为加入了L2,1范数惩罚项，使得到的投影矩阵行稀疏，自动抛弃了一些对分类没用的特征，有利于特征的选取，同时也能防止过拟合问题，提升模泛化能力。如L21GKDA算法的识别率在多数情况下明显高于KDA，L21FLDA算法的识别率明显高于Fisherfaces，这都得益于L2,1范数正则化方法。而SDA算法，由于在子空间的各个维度上所选取的特征均不相同，故识别效果并不理想。

从表2～表4中也可以看出，非线性方法的识别率优于线性方法，因为非线性方法能发现图像高阶非线性信息，所以识别率较高。如L21GKDA与L21FLDA相比，也就是非线性方法与线性方法相比，核方法有效提高了算法性能，并且核方法中核矩阵的维数等于训练样本总数，当训练样本总数小于原始样本特征维数时，算法中特征分解所用时间也大大减少。

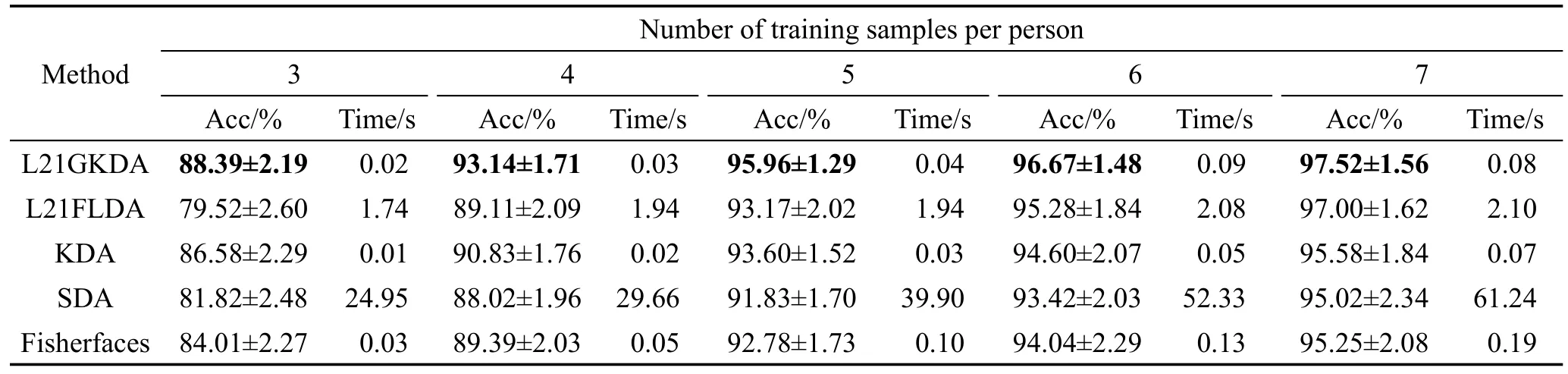
Table 2 Average recognition accuracies,standard deviations and running time on ORL face database表2 ORL人脸库上各算法的平均识别率、标准差和时间

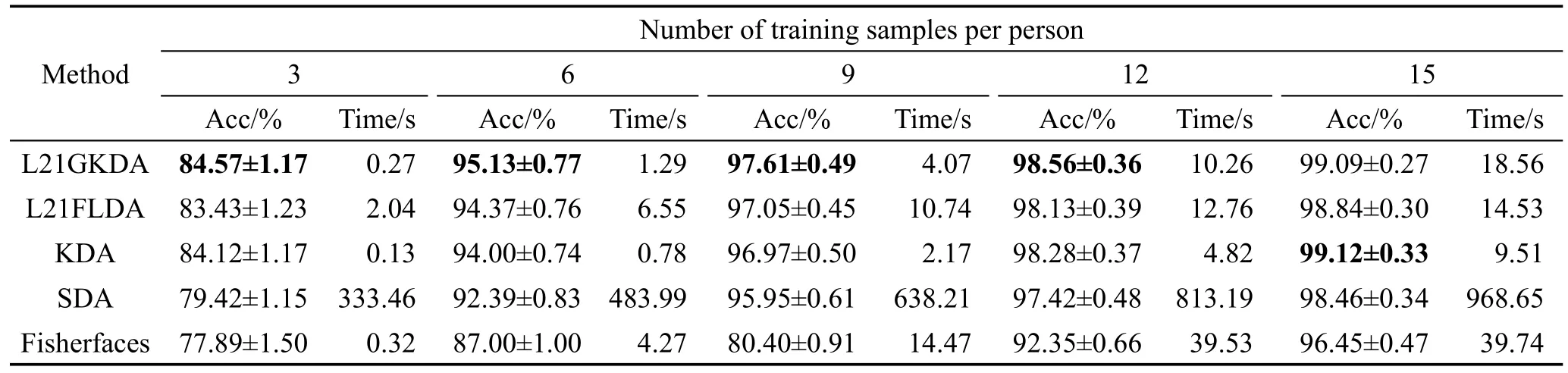
Table 3 Average recognition accuracies,standard deviations and running time onAR face database表3 AR人脸库上各算法的平均识别率、标准差和时间

Table 4 Average recognition accuracies,standard deviations and running time on PIE face database表4 PIE人脸库上各算法的平均识别率、标准差和时间

4.2.5 特征维数对实验的影响

目前，国内普遍采用预处理+生化处理+膜深度处理工艺处理垃圾渗沥液。其中，生化处理一般采用硝化-反硝化+MBR工艺，以保证脱氨效果。生物处理反硝化单元中主要为异养菌，异养菌脱氮过程主要是针对硝化过程中产生的硝氮进行反硝化脱氮。整个过程中典型的硝化反应过程如公式（1）所示，氨氮在自养菌作用下硝化形成硝氮，硝氮在异养菌作用下反硝化形成氮气，如公式（2）所示，从而完成脱氮。反硝化过程需要消耗有机物［1］，因此，需要保证废水中有足够的有机碳源。

该小节通过实验讨论特征维数与平均识别率的关系。其中在ORL人脸库上每人随机取5幅图像作为训练样本，AR人脸库上每人取9幅，PIE人脸库上每人取20幅，余下图像作为测试样本。特征维数从1取到C-1维，其关系如图5所示。

Fig.5 Relationship between average recognition accuracy and dimensions图5 平均识别率与特征维数的关系图

由图5可知，算法的识别率均随着特征维数的增加而增加，加入L2,1范数惩罚项的算法识别率增加较快，在较低特征维数时就能达到良好的识别效果。如L21GKDA与KDA相比，在绝大多数维度下，L21GKDA算法的识别率比KDA高；同样，L21FLDA算法的识别率在取不同维度时也比Fisherfaces高。且当维度取到C-1时，L21GKDA算法识别率最高，这说明联合特征选取和子空间学习方法能有效选取特征，提高算法的识别率。同时，也可以看出，基于核方法的算法相对于线性方法在处理人脸识别问题上显得更为有效。

5 结束语

[1]Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.

本文提出了L2,1范数正则化的广义核判别分析，首先给出了核方法的原理及KDA的求解方法，然后针对如何加入L2,1范数惩罚项，使特征选取和子空间学习同时进行，给出了具体的解决方法，同时也解决了KDA算法的奇异性问题。最后在标准人脸库上的实验结果表明，当人脸的表情、姿态、光照等发生变化时，本文算法具有良好的识别性能，从而说明该算法既能有效地对高维数据降维，消除冗余信息，又能选取数据的有用特征，提高鉴别能力。将联合特征选取和子空间学习方法应用于其他具有代表性的判别分析算法中，如直接线性判别分析，值得进一步的研究。

[2]Belhumeur P N,Hespanha J P,Kriegman D.Eigenfaces vs. Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[3]He Xiaofei,Niyogi P.Locality preserving projections[J]. Advances in Neural Information Processing Systems,2005, 45(1):186-197.

机器学习中常用正则化方法来约束模型的特性，而加入不同的惩罚项带来的特性也不同。例如，加入L1范数能使模型稀疏，加入L2范数能避免出现过拟合问题，提升模型的泛化能力。文献[9]提出了一种联合特征选取和子空间学习的方法，通过加入L2,1范数惩罚项，使学习到的投影矩阵行稀疏。文献[10]证明了该算法的收敛性。文献[11]给出了一个提高人脸判别能力的框架。随后，Shi等人[12]首次将其应用于Fisher判别分析，一定程度上提高了人脸识别的性能。

[4]Jin Zhong,Yang Jingyu,Hu Zhongshan,et al.Face recognition based on the uncorrelated discriminant transformation [J].Pattern Recognition,2001,34(7):1405-1416.

[5]Jin Zhong,Yang Jingyu,Tang Zhenmin,et al.A theorem on the uncorrelated optimal discriminant vectors[J].Pattern Recognition,2001,34(10):2041-2047.

下面对Ey=λy进行特征分解。通过特征分解的基本知识可以得到，矩阵E是块对角矩阵，那么它的特征值和特征向量由其对应对角块的特征值和特征向量组成。可以发现，对角块的特征值1所对应的特征向量为，并且rank(Ei)= 1，即Ei只有唯一的非零特征值1。最终得到E有C个特征向量，其特征值均为1。这些特征向量yd如下所示：

[7]Lai Zhihui,Xu Yong,Yang Jian,et al.Sparse tensor discriminant analysis[J].IEEE Transactions on Image Processing, 2013,22(10):3904-3915.

三是学校排课更轻松。传统会计教学模式下，由于受班级数量、学生人数、学习地点、上课时间等限制，以及任课教师数量、能力、精力等影响，学校在编排课表时煞费苦心、焦头烂额，也不一定能达到预期目的。在网络课堂情况下，这些问题都不复存在，迎刃而解，不但大大节省了学校办学成本，还解放了一部分会计专业教师，使他们有更多精力从事更深入的教学研究或教学实践活动，以进一步提高会计教学质量，增强学生就业能力。

[8]Zou Hui,Hastie T,Tibshirani R.Sparse principal component analysis[J].Journal of Computational and Graphical Statistics,2006,15(2):265-286.

[9]Obozinski G,Taskar B,Jordan M I.Joint covariate selection and joint subspace selection for multiple classification problems[J].Statistics and Computing,2010,20(2):231-252. [10]Nie Feiping,Huang Heng,Cai Xiao,et al.Efficient and robust feature selection via joint ℓ 2,1-norms minimization [C]//Advances in Neural Information Processing Systems 23:Proceedings of the 24th Annual Conference on NeuralInformation Processing Systems,Vancouver,Canada,Dec 6-9,2010.Vancouver,Canada:Curran Associates,2010: 1813-1821.

[11]Gu Quanquan,Li Zhenhui,Han Jiawei.Joint feature selection and subspace learning[C]//Proceedings of the 22nd International Joint Conference on Artificial Intelligence,Barcelona,Spain,Jul 16-22,2011.Menlo Park,USA:AAAI, 2011:1294-1299.

[12]Shi Xiaoshuang,Yang Yujiu,Guo Zhenhua,et al.Face recognition by sparse discriminant analysis via joint L2,1-norm minimization[J].Pattern Recognition,2014,47(7):2447-2453.

1.2.2.2 溶栓过程中的护理[4] 。患者病发3 h内需尽快进行静脉溶栓治疗，需注意阿替普酶不能使用葡萄糖、灭菌注射用水进行稀释和混合。治疗过程中需安排专业的护师对患者生命体征和病情变化进行监测，维持血压稳定，若血压过高需配合医生进行降压治疗。若患者出现口舌、喉头、血管源性水肿症状，以及呼吸困难、烦躁不安、发绀时，需立即停止用药，并给予抗过敏治疗，同时准备好呼吸机和气管切开工具，给予面罩大流量吸氧。此外，还需注意患者意识状态和肢体障碍、新发生的恶心、头痛、呕吐、颅内出血等症状。

[13]Mika S,Ratsch G,Weston J,et al.Fisher discriminant analysis with kernels[C]//Proceedings of the 1999 IEEE Signal Processing Society Workshop,Neural Networks for Signal Processing IX,Madison,USA,Aug 25,1999.Piscataway, USA:IEEE,1999:41-48.

常见抗病毒治疗药物因为其药物代谢途径、毒副作用等特点，与很多其他种类药物产生药物相互作用。临床中要密切关注患者合并用药情况，并参考其他相关指南或药物说明书及时调整药物方案或调整药物剂量。

[14]Yang M H.Kernel eigenfaces vs.kernel fisherfaces:face recognition using kernel methods[C]//Proceedings of the 5th IEEE International Conference on Automatic Face and Gesture Recognition,Washington,May 21-21,2002.Piscataway,USA:IEEE,2002:215-220.

[15]Baudat G,Anouar F.Generalized discriminant analysis using a kernel approach[J].Neural Computation,2000,12(10): 2385-2404.

[16]Martinez AM,Benavente R.The AR face database,CVC technical report 24[R].1998.

[17]Sim T,Baker S,Bsat M,The CMU pose,illumination,and expression database[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(12):1615-1618.

辅导班是另一种学习方法，它是在学习书本知识之后进行的课后辅导，一般通过老师的讲解，自己的多次练习去学习，对掌握的知识进行再次巩固。这种现象也最常见在我们的学生当中，学生们从刚开始上学就开始被安排上各种辅导班，有学舞蹈，有学画画，到了大学毕业后，通过各种专业的考研辅导、国家公务员考试等辅导班，来强化各种能力。尤其在现在的社会中竞争激烈，辅导班的学习也逐渐成为潮流。

FU Junpeng was born in 1991.He is an M.S.candidate at Jiangnan University.His research interests include image processing and pattern recognition,etc.

傅俊鹏（1991—），男，浙江义乌人，江南大学硕士研究生，主要研究领域为数字图像处理，模式识别等。

CHEN Xiuhong was born in 1964.He received the Ph.D.degree from East China University of Science and Technology in 2000.Now he is a professor and M.S.supervisor at Jiangnan University,and the member of CCF.His research interests include image processing and pattern recognition,etc.

陈秀宏（1964—），男，江苏泰州人，2000年于华东理工大学获得博士学位，现为江南大学教授、硕士生导师，CCF会员，主要研究领域为数字图像处理，模式识别等。发表学术论文100余篇，先后参加国家自然科学基金3项、江苏省自然科学基金1项，主持省部级研究项目3项，省博士后基金1项等。

GE Xiaoqian was born in 1990.She is an M.S.candidate at Jiangnan University.Her research interests include image processing and pattern recognition,etc.

葛骁倩（1990—），女，江苏南通人，江南大学硕士研究生，主要研究领域为数字图像处理，模式识别等。

Face Recognition by Generalized Kernel Discriminant Analysis viaL2,1-Norm Regularization*

FU Junpeng+,CHEN Xiuhong,GE Xiaoqian
School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:fujunpeng2@163.com

Feature selection and subspace learning are two key problems in face recognition.To select the rich nonlinear features more accurately in face image and solve the small sample size problem,this paper proposes a new generalized kernel discriminant analysis based onL2,1-norm regularization(L21GKDA).The proposed method implicitly maps the original samples into feature space by using kernel function,and obtains the generalized kernel Fisher criterion. Then it presents an efficient transformation,transforming its nonlinear model into linear regression model.In order to perform feature selection and subspace learning simultaneously,anL2,1-norm penalty term is added to the objective function,and the solution algorithm of the regularization method is also obtained.Due to the feature selection capability ofL2,1-norm penalty term,the recognition performance is greatly improved.Experiments on ORL,AR,PIE standard face databases illustrate that the new method can effectively select the nonlinear features of the face data,and improve the discriminant ability.

face recognition;feature selection;subspace learning;L2,1-norm;kernel discriminant analysis

A

：TP391

10.3778/j.issn.1673-9418.1510052

*The National Natural Science Foundation of China under Grant No.61373055(国家自然科学基金).

Received 2015-10,Accepted 2016-01.

CNKI网络优先出版:2016-01-13,http://www.cnki.net/kcms/detail/11.5602.TP.20160113.0933.002.html