IPOWA算子及其在正态随机多准则决策中的应用*

任 剑，成鹏飞，周向红

1.湖南大学 工商管理学院，长沙 410082

2.湖南商学院 湖南省移动电子商务协同创新中心，长沙 410205

3.湖南科技大学 管理学院，湖南 湘潭 411201

IPOWA算子及其在正态随机多准则决策中的应用*

任 剑1,2，成鹏飞3+，周向红3

1.湖南大学 工商管理学院，长沙 410082

2.湖南商学院 湖南省移动电子商务协同创新中心，长沙 410205

3.湖南科技大学 管理学院，湖南 湘潭 411201

REN Jian,CHENG Pengfei,ZHOU Xianghong.IPOWA operator and its application in normal stochastic multi-criterion decision-making.Journal of Frontiers of Computer Science and Technology,2017,11(1):155-162.

现实中，很多现象近似服从正态分布。为了解决准则值为正态随机变量且决策者风险态度不确定的多准则决策问题，提出了一种基于区间可能有序加权平均（interval possible ordered weighted averaging，IPOWA）算子与可能性系数的方法。通过正态随机变量的线性组合方法，算出各方案的线性加权正态随机变量。根据正态随机变量的3σ原则，将线性加权正态随机变量转化为随机区间数。对随机区间数进行两两比较，得到可能度矩阵，利用区间可能有序加权平均算子，集结可能度矩阵中每行元素的值。采用风险态度的可能性系数，计算各方案的综合评价值，进而确定各方案的最终排序。最后，通过两个算例的对比分析，表明所提方法具有排序结果稳定，支持信息充分等特点。

多准则决策；正态随机变量；区间可能有序加权平均算子；可能度矩阵；风险态度的可能性系数

1 引言

正态随机变量的概率密度函数总体上呈现“两头低，中间高”的特征，在数学、物理及工程等领域有着很重要的理论价值和应用价值。中心极限定理指出：大多数独立同分布的随机事件，整体上服从正态分布。在实际随机多准则决策中，若缺乏对准则值随机性的深入了解以及无法获取充足决策信息，则随机准则值的概率或概率密度函数难以确定。此时，可将大多数随机准则值近似为服从正态分布。由于这种方式在处理随机不确定性上更具灵活性和实用性，引起众多学者的关注。

在正态随机多准则决策领域，主要有以下研究方法：（1）仿真法。刘琳等人采用模糊随机仿真法得到正态分布区间属性值的综合评估值[1]。（2）算子法。王坚强等人提出一种基于方案贴近度与加权连续区间有序加权平均（weighted continuous-intervalargument ordered weighted averaging，WC-OWA）算子的正态随机多准则决策方法[2]。汪新凡等人定义了正态分布区间数的加权算术平均（weighted arithmetic averaging，WAA）算子、有序加权平均（ordered weighted averaging，OWA）算子和混合加权平均（hybrid weighted averaging，HWA）算子，求解正态分布区间多准则群决策问题[3]。（3）Outranking法。姜广田等人先后运用PROMETHEE法、随机占优关系与ELECTREⅢ法求解正态随机多准则决策问题[4-5]。（4）可能度法。徐改丽等人根据离差最大化原理确定准则权重，利用可能度法对正态分布区间数进行排序[6]。（5）行为决策法。陈振颂等人基于前景均值-方差准则，求解正态三角模糊随机多属性决策问题[7]。上述方法大多数结合区间数或模糊数的性质，处理正态分布的准则值，且考虑了准则权重不完全确定或未知情形，较好解决了正态随机多准则决策问题。然而，对于决策者的风险态度由于情绪、环境等变化可能导致的不确定性，没有深入探讨。

连续型信息集结算子可有效处理正态分布的准则值，且考虑了决策者风险偏好、风险中立、风险规避等类型，在正态随机多准则决策领域有着很好的应用前景。最常见的是连续区间有序加权平均（continuous-interval-argument ordered weighted averaging, C-OWA）算子及其拓展形式。Yager为了集结区间数，提出C-OWA算子[8]。徐泽水基于此，定义了加权C-OWA（WC-OWA）算子，用来处理两个以上区间的数据集结[9]。Yager等人定义了（continuous ordered weighted geometric,C-OWG）算子，应用于具有区间乘性偏好关系的决策中[10]。Zarghamia等人提出模糊随机修正OWA算子进行不确定性多准则决策，并应用于流域管理中[11]。Zhou等人定义了连续泛型OWA算子、加权连续泛型OWA算子、有序加权连续泛型OWA算子、组合连续泛型OWA算子、组合连续泛型丘奎特积分集结（combined continuous generalized Choquet integral aggregation,CC-GCIA）算子，并利用这些拓展的连续泛型OWA算子进行有区间数的群决策[12]。Zeng等人定义了不确定概率有序加权平均距离（uncertain probabilistic ordered weighted averaging distance,UPOWAD）算子，应用于区间多准则群决策问题中[13]。上述算子已经成功应用于区间数决策问题中。鉴于正态随机变量可近似转化为区间数，本文定义了区间可能有序加权平均（interval possible ordered weighted averaging，IPOWA）算子，考虑决策者的不同风险偏好类型及其可能性系数，构建相应的正态随机多准则决策方法，并应用于城市雨涝灾害风险承受能力综合评估问题和多指标电力零售商选择问题中进行算例分析。

2 正态随机变量

2.1 正态随机变量的线性组合方法

定理1[14]若有n个相互独立的正态随机变量，则服从正态分布。

定理2[14]若有n个相互独立的正态随机变量，则服从正态分布。

2.2 正态随机变量的3σ原则

在准则值为正态随机变量的多准则决策中，若决策者无法获得更多准则的取值信息，则可将正态随机变量近似为有限区间上服从均匀分布的随机变量，可用区间数α=[αL,αR]表示这样的随机有限区间，满足下列条件[2]：

3 IPOWA算子

4 风险态度的可能性系数

通常，决策者的风险态度会根据不同的决策情景表现出不确定性。例如：当股市低迷时，大多数中小股民减少股票投资；当股市趋好时，大多数中小股民加大股票投资。因此，引入风险态度的可能性系数。

定义4设α为风险偏好的可能性系数，β为风险中立的可能性系数，γ为风险规避的可能性系数，其中α，β，γ∈[0 ,1]，且α+β+γ=1。

风险态度的可能性系数可以根据历史数据统计、行为实验设计、主观概率估计等方式获得。

基于风险态度的可能性系数，方案ai的综合评价值为(i∈M)：

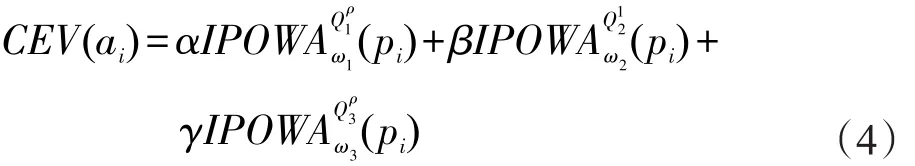
5 IPOWA算子在正态随机多准则决策中的应用

5.1 问题描述

在某一个多准则决策问题中，设有m个备选方案，记为A={a1,a2,…,am}；n个相互独立的评价准则，记为C={C1,C2,…,Cn}；W=(w1,w2,…,wn)表示准则权重向量，wj是准则Cj的权重(j∈N)，0≤wj≤1且；正态随机决策矩阵记为NSDM=(xij)m×n，xi(i∈M)是正态随机变量集，表示方案ai在准则集C下的优劣表现，xij(i∈M,j∈N)是正态随机变量，表示方案ai在准则Cj下的优劣表现；确定方案集A的排序。

5.2 决策步骤

步骤1根据正态随机变量的线性组合方法，利用定理2，求得方案ai在准则集C下的线性加权正态随机变量yi服从正态分布。

步骤2根据正态随机变量的3σ原则，利用式（1）和式（2），将线性加权正态随机变量yi转化为随机区间数。

步骤3利用定义2，对随机区间数αi进行两两比较(i∈M)，得到可能度矩阵P=(pij)m×m。

步骤4利用定义3，求得、。

步骤5确定风险态度的可能性系数α、β、γ，利用式（4），计算方案ai的综合评价值CEV(ai)(i∈M)。

步骤6根据CEV(ai)(i∈M)的大小，对方案集A进行排序。

Table 1 Normal stochastic decision-making matrix表1 正态随机决策矩阵

6 算例分析

6.1 城市雨涝灾害风险承受能力综合评估的算例分析

近年来，由于极端气候及我国城市“摊大饼式”建设等原因，导致城市雨涝灾害频发，造成严重的财产损失，危及人民生命安全，城市雨涝灾害风险承受能力评估已成为亟待破解的新难题。某市水务管理部门决策者对本市3个城市片区A={a1,a2,a3}的雨涝灾害风险承受能力进行综合评估。基于成灾模式分析，确定评估雨涝灾害风险承受能力的指标体系C= {C1,C2,…,C6}：渗水能力C1、蓄水能力C2、排水能力C3、用水能力C4、救援能力C5、治水能力C6。指标权重向量W=(0.12,0.15,0.18,0.25,0.20,0.10)。正态随机决策矩阵如表1所示。试评估各城市片区的雨涝灾害风险承受能力。

利用定理2，求得方案ai在准则集C下的线性加权正态随机变量yi(i∈M={1,2,3})如表2所示。

Table 2 Linear weighted normal stochastic variablesyi(i∈M)表2 线性加权正态随机变量yi(i∈M)

利用式（1）和式（2），将线性加权正态随机变量yi转化为随机区间数αi(i∈M)如表3所示。

Table 3 Stochastic interval numbersαi(i∈M)表3 随机区间数αi(i∈M)

得到可能度矩阵P=(pij)3×3如表4所示。

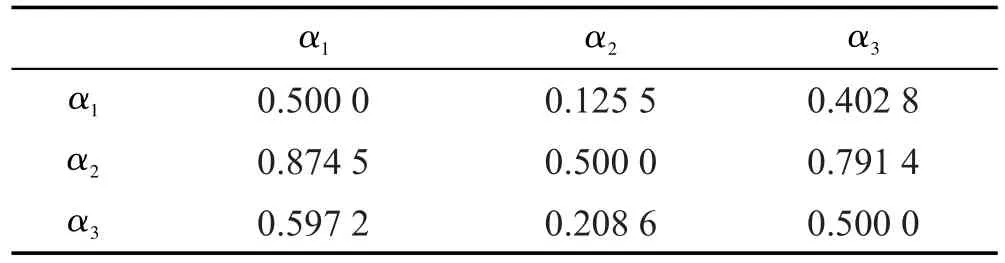
Table 4 Possible degree matrixP表4 可能度矩阵P

根据决策者不同的风险偏好进行处理：当决策者为风险偏好型时，取Q1(x)=x12，ω1≈(0.577 4,0.239 1, 0.183 5)；当决策者为风险中立型时，取Q2(x)=x，ω2≈(0.333 3,0.333 3,0.333 3)；当决策者为风险规避型时，取Q3(x)=x2，ω3≈(0.111 1,0.333 3,0.555 6)。

Table 5 Result by interval possible ordered weighted averaging operator表5 区间可能有序加权平均算子的计算结果

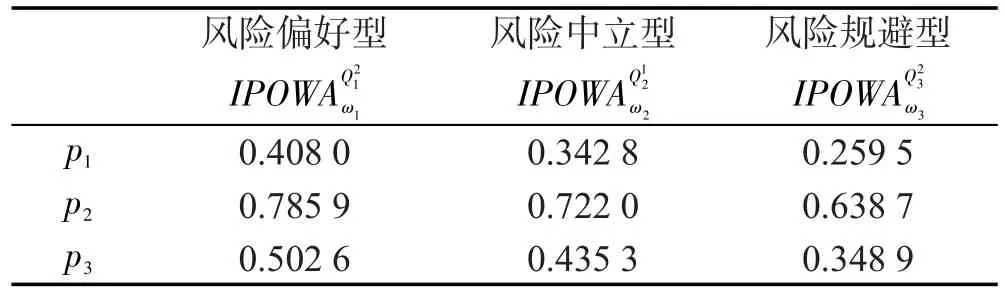
Table 5 Result by interval possible ordered weighted averaging operator表5 区间可能有序加权平均算子的计算结果

风险偏好型IPOWAQ21 2 3ω1风险中立型IPOWAQ1ω2风险规避型IPOWAQ2ω3p1p2p3 0.408 0 0.785 9 0.502 6 0.342 8 0.722 0 0.435 3 0.259 5 0.638 7 0.348 9

利用本文方法获得方案ai(i∈M)的排序结果，如表6所示。

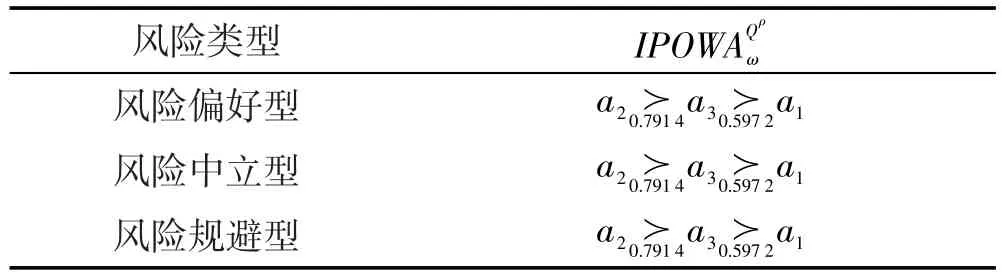
Table 6 Ranking result of alternatives by IPOWAoperator表6 IPOWA算子得到的方案排序结果

Table 7 Comprehensive evaluation value表7 综合评价值

方案集A的排序结果为：。

下面对本算例进行比较分析。

随机模拟法是最常用的处理随机变量的方法。文献[16]提出一种云加权算术平均（cloud weighted arithmetic averaging，CWAA）算子集结云模型，并利用随机模拟法处理集结云模型。云模型是一种泛型的正态随机变量。根据类似思路，对表2中的线性加权正态随机变量yi，以10为增量，随机模拟10次到1 000次，并计算每回的均值，可得结果如图1所示。从图1中不难发现：y1、y2、y3的模拟结果较为稳定，即a2≻a3≻a1。

Fig.1 Result of stochastic simulation method图1 随机模拟法的结果

区间数可能度矩阵的排序向量法是较常用的比较区间数优劣的方法[6]。

可能度矩阵P=(pij)m×m的排序公式为：

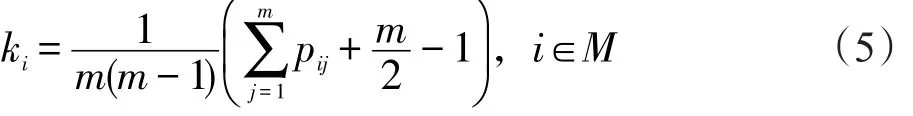
利用式（5）可得排序向量K=(k1,k2,…,km)，比较ki(i∈M)的大小可得区间数的排序。

根据上述方法，求得表4中可能度矩阵P的排序向量K=(0.254 7,0.444 3,0.301 0)，并得到方案的排序结果：。

比较随机模拟法、排序向量法、IPOWA算子法的排序情况，可得以下结论：

（1）三者得到了较一致的排序结果；

（2）随机模拟法只考虑了决策者风险中立的情形，且没有指示排序可能性大小的辅助信息；

（3）排序向量法具有指示排序可能性大小的辅助信息，但没有考虑决策者的风险态度；

（4）IPOWA算子法既有指示排序可能性大小的辅助信息，也考虑了决策者的不同风险态度及其动态变化，另外所得排序结果的离差较大，对方案的区分度较好。

6.2 多指标电力零售商选择的算例分析

为了更进一步检验本文方法的性能，下面利用文献[5]中的算例数据进行对比分析。

当决策者为风险偏好型时，取Q′1(x)=x13，ω′1≈(0.480 7,0.125 0,0.087 7,0.069 8,0.058 9,0.051 5,0.046 1, 0.041 9,0.038 5)；当决策者为风险中立型时，取Q′2(x)=x,ω′2≈(0.1111,0.1111,0.1111,0.1111,0.1111,0.111 1, 0.111 1,0.111 1,0.111 1)；当决策者为风险规避型时，取Q′3(x)=x3，ω′3≈(0.001 4,0.009 6,0.026 1,0.050 8, 0.083 7,0.124 8,0.174 2,0.231 8,0.297 7)。

利用本文方法获得方案ai(i∈M)的排序结果为：

（1）若决策者为风险偏好型

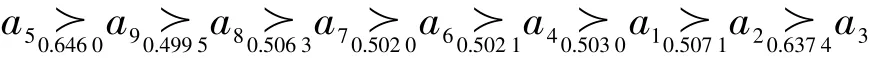
（2）若决策者为风险中立型

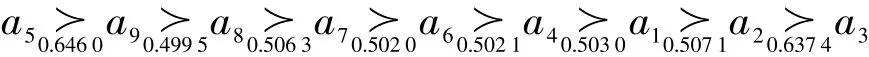
Table 8 Result by interval possible ordered weighted averaging operator表8 区间可能有序加权平均算子的计算结果

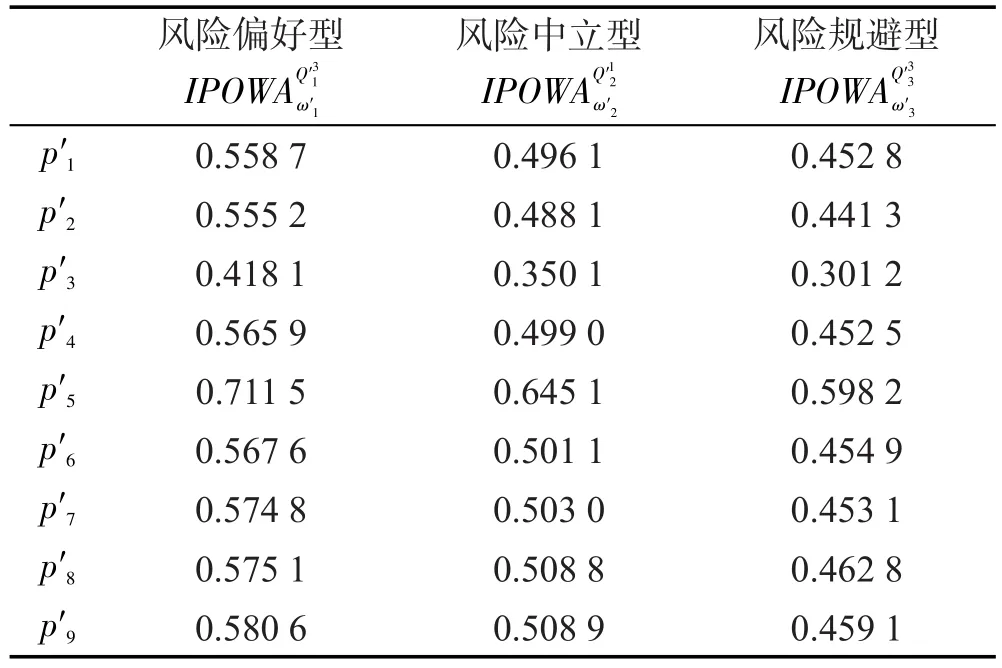
Table 8 Result by interval possible ordered weighted averaging operator表8 区间可能有序加权平均算子的计算结果

风险偏好型IPOWAQ′31 2 3ω′1风险中立型IPOWAQ′1ω′2风险规避型IPOWAQ′3ω′3p′1p′2p′3p′4p′5p′6p′7p′8p′9 0.558 7 0.555 2 0.418 1 0.565 9 0.711 5 0.567 6 0.574 8 0.575 1 0.580 6 0.496 1 0.488 1 0.350 1 0.499 0 0.645 1 0.501 1 0.503 0 0.508 8 0.508 9 0.452 8 0.441 3 0.301 2 0.452 5 0.598 2 0.454 9 0.453 1 0.462 8 0.459 1

（3）若决策者为风险规避型

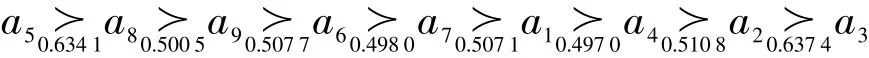
在各种风险偏好情况下：决策者为风险偏好型和风险中立型时，排序结果完全一致；决策者为风险规避型时，排序结果与前两种情况总体相近。在a8与a9、a6与a7、a1与a4三对方案上，的优劣顺序相同，但三对方案内出现逆序，比较三对方案内两个方案间的排序可能度，均非常接近0.5，因此三对方案内两个方案间优劣相当。

当综合三种情况时，可得方案集排序结果为：

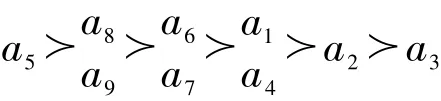
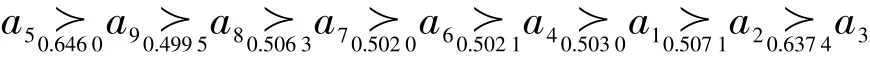
通过本文方法与文献[5]的排序结果对比可知：两者排序结果总体相近，本文方法不需要准则阈值等辅助决策信息，计算步骤清晰，过程简便。在a7与a8、a4与a6、a1与a2三对方案上，的优劣顺序相同，但三对方案内出现逆序，比较三对方案内两个方案间的排序可能度，均非常接近0.5，因此三对方案内两个方案间优劣相当。

综上分析，本文方法比传统方法具有更好的排序结果和分析手段，性能优良。

7 结束语

本文介绍了正态随机变量的线性组合方法和3σ原则，在分析有序加权平均算子的性质后，定义了IPOWA算子与风险态度的可能性系数，并提出了一种基于IPOWA算子与可能性系数的正态随机多准则决策方法。最后通过两个算例的对比分析，显示本文方法具有以下优点：（1）将OWA算子引入区间数排序的可能度方法中，考虑决策者风险偏好、风险中立、风险规避三种风险态度；（2）引入风险态度的可能性系数，考虑不同决策情景引起决策者风险态度不确定的情形；（3）排序结果稳定性较高，且有更多决策支持信息，如排序可能度，可进行决策结果分析。

[1]Liu Lin,Chen Yunxiang,Ge Zhihao.Probability measure of interval-number based on normal distribution and multiattribute decision making[J].Systems Engineering and Electronics,2008,30(4):652-654.

[2]Wang Jianqiang,Ren Jian.Stochastic multi-criteria decisionmaking method based on WC-OWA operator[J].Control and Decision,2007,22(12):1429-1432.

[3]Wang Xinfan,Xiao Mansheng.Approach of group decision making based on normal distribution interval number with incomplete information[J].Control and Decision,2010,25(10): 1494-1498.

[4]Jiang Guangtian,Fan Zhiping,Liu Yang,et al.Method for multiple attribute decision making with normal random variables[J].Control and Decision,2009,24(8):1187-1197.

[5]Jiang Guangtian,Fan Zhiping.A method for MADM with normal random variables[J].Control and Decision,2012,32 (7):1517-1524.

[6]Xu Gaili,Lv Yuejin.Approach of multi-attribute decisionmaking based on normal distribution interval number[J]. Systems Engineering,2011,29(9):120-123.

[7]Chen Zhensong,Li Yanlai.Approach for normal triangular fuzzy stochastic multiple attribute decision making based on prospect mean-variance rule[J].Control and Decision, 2014,29(7):1239-1248.

[8]Yager R R.OWAaggregation over a continuous interval argument with applications to decision making[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B,2004,34 (5):1952-1963.

[9]Xu Zeshui.Extended C-OWA operators and their use in uncertain multi-attribute decision making[J].Systems Engineering-Theory&Practice,2005,25(11):7-13.

[10]Yager R R,Xu Zeshui.The continuous ordered weighted geometric operator and its application to decision making [J].Fuzzy Sets and Systems,2006,157(10):1393-1402.

[11]Zarghamia M,Szidarovszky F.Revising the OWA operator for multi criteria decision making problems under uncertainty[J].European Journal of Operational Research,2009, 198(1):259-265.

[12]Zhou Ligang,Chen Huayou.Continuous generalized OWA operator and its application to decision making[J].Fuzzy Sets and Systems,2011,168(1):18-34.

[13]Zeng Shouzhen,Merigó J M,Su Weihua.The uncertain probabilistic OWA distance operator and its application in group decision making[J].Applied Mathematical Modelling, 2013,37(9):6266-6275.

[14]Shen Hengfan.A course in probability theory and mathematical statistics[M].Beijing:Higher Education Press,1995: 145.

[15]Wan Shuping,Dong Jiuying.A possibility degree method for interval-valued intuitionistic fuzzy multi-attribute group decision making[J].Journal of Computer and System Sciences,2014,80(1):237-256. [16]Wang Jianqiang,Peng Lu,Zhang Hongyu,et al.Method of multi-criteria group decision-making based on cloud aggregation operators with linguistic information[J].Information Sciences,2014,274(8):177-191.

附中文参考文献：

[1]刘琳,陈云翔,葛志浩.基于正态分布区间数的概率测度及多属性决策[J].系统工程与电子技术,2008,30(4):652-654.

[2]王坚强,任剑.基于WC-OWA算子的随机多准则决策方法[J].控制与决策,2007,22(12):1429-1432.

[3]汪新凡,肖满生.基于正态分布区间数的信息不完全的群决策方法[J].控制与决策,2010,25(10):1494-1498.

[4]姜广田,樊治平,刘洋,等.一种具有正态随机变量的多属性决策方法[J].控制与决策,2009,24(8):1187-1197.

[5]姜广田,樊治平.属性值为正态随机变量的多属性决策方法[J].控制与决策,2012,32(7):1517-1524.

[6]徐改丽,吕跃进.基于正态分布区间数的多属性决策方法[J].系统工程,2011,29(9):120-123.

[7]陈振颂,李延来.基于前景M-V准则的正态三角模糊随机多属性决策方法[J].控制与决策,2014,29(7):1239-1248.

[9]徐泽水.拓展的C-OWA算子及其在不确定多属性决策中的应用[J].系统工程理论与实践,2005,25(11):7-13.

[14]沈恒范.概率论与数理统计教程[M].北京:高等教育出版社,1995:145.

REN Jian was born in 1979.He received the Ph.D.degree in management science and engineering from Central South University in 2010.Now he is an associate professor and M.S.supervisor at Hunan University of Commerce. His research interests include electronic commerce,decision theory and method,etc.

任剑（1979—），男，湖南岳阳人，2010年于中南大学管理科学与工程专业获得博士学位，目前在湖南大学从事博士后研究工作，湖南商学院副教授、硕士生导师，主要研究领域为电子商务，决策理论与方法等。

CHENG Pengfei was born in 1969.He received the Ph.D.degree in management science and engineering from Central South University in 2008.Now he is a professor and M.S.supervisor at Hunan University of Science and Technology.His research interests include electronic commerce,decision theory and method,etc.

成鹏飞（1969—），男，湖南湘乡人，2008年于中南大学管理科学与工程专业获得博士学位，现为湖南科技大学教授、硕士生导师，主要研究领域为电子商务，决策理论与方法等。

ZHOU Xianghong was born in 1981.He received the Ph.D.degree in management science and engineering from Central South University in 2015.Now he is a lecturer at Hunan University of Science and Technology.His research interests include electronic commerce,decision theory and method,etc.

周向红（1981—），男，湖南新邵人，2015年于中南大学管理科学与工程专业获得博士学位，现为湖南科技大学讲师，主要研究领域为电子商务，决策理论与方法等。

IPOWAOperator and ItsApplication in Normal Stochastic Multi-Criterion Decision-Making*

REN Jian1,2,CHENG Pengfei3+,ZHOU Xianghong3
1.School of Business,Hunan University,Changsha 410082,China
2.Mobile E-business Collaborative Innovation Center of Hunan Province,Hunan University of Commerce,Changsha 410205,China
3.School of Management,Hunan University of Science and Technology,Xiangtan,Hunan 411201,China
+Corresponding author:E-mail:chengpengfei69@126.com

In reality,most of the phenomena can approximately obey the normal distribution.In order to solve multicriterion decision-making problems with normal stochastic criterion evaluations and uncertain risk attitude of decision makers,this paper proposes a method based on interval possible ordered weighted averaging(IPOWA)operatorand possibility coefficients.Firstly,by the linear combination method of normal stochastic variables,the linear weighted normal stochastic variables of alternatives are gotten.Then,according to the3σprinciple of normal stochastic variables,the linear weighted normal stochastic variables are transformed into stochastic interval numbers. Furthermore,through the comparison of stochastic interval numbers,the possible degree matrix is attained.After that,using the IPOWA operator,the items of each row are integrated in the matrix.Accordingly,via the possibility coefficients of risk attitudes,the comprehensive evaluation values of alternatives are calculated.Moreover,the ranking order comes out.Finally,the comparative analysis of two illustrative examples shows the method has some features such as stable ranking result,sufficient support information and so on.

multi-criterion decision-making;normal stochastic variable;interval possible ordered weighted averaging operator;possible degree matrix;possibility coefficient of risk attitude

A

：C934

10.3778/j.issn.1673-9418.1604038

*The National Social Science Foundation of China under Grant No.15BJY163(国家社会科学基金);the Humanities and Social Science Foundation for Youth of Ministry of Education of China under Grant No.13YJCZH145(教育部人文社会科学研究青年基金); the Postdoctoral Science Foundation of China under Grant No.2013M531784(中国博士后科学基金);the Philosophy and Social Science Foundation of Hunan Province under Grant No.15JD21(湖南省哲学社会科学基金);the Major Project of the Social Science Achievement Evaluation Committee of Hunan Province under Grant No.XSP2016040508(湖南省社会科学成果评审委员会重大课题);the Scientific Research Project for the Outstanding Youth of Department of Education of Hunan Province under Grant No. 15B129(湖南省教育厅科学研究优秀青年项目).

Received 2016-04,Accepted 2016-08.

CNKI网络优先出版:2016-08-15,http://www.cnki.net/kcms/detail/11.5602.TP.20160815.1659.018.html