光电跟瞄平台稳定控制器设计*

刘珊中，李燕凡，刘永斌，屈秀敏

（河南科技大学信息工程学院，河南洛阳471023）

光电跟瞄平台稳定控制器设计*

刘珊中，李燕凡，刘永斌，屈秀敏

（河南科技大学信息工程学院，河南洛阳471023）

以考虑光电跟瞄平台三轴环架间的耦合所建立的数学模型为基础，对光电跟瞄平台的稳定回路分别设计了基于线性矩阵不等式（LMI）的状态反馈H∞控制器和多输入系统极点配置控制器；分别建立基于所设计两种控制器的跟瞄平台稳定控制系统，并对其控制效果进行对比研究，结果表明，二者皆能实现对光电跟瞄平台的稳定控制，都具有一定的鲁棒性能。其中H∞控制器的设计更简单，超调更小且达到稳定的时间短，更适合于光电跟瞄平台的稳定控制。

光电跟瞄平台，状态反馈H∞控制，极点配置，鲁棒性

0 引言

光电跟瞄平台三轴环架间存在复杂的耦合关系，在机载环境下又易受到各种扰动影响。为了实现精确地跟踪指定目标，设计鲁棒性好和抗干扰能力强的稳定控制器是光电跟瞄平台控制系统设计的关键。国内外学者对此进行了很多研究，其中以目前最常用的不考虑环架间耦合建立的数学模型为研究对象，见文献［1-4］。

H∞控制是为多输入多输出（MIMO）且具有模型摄动的系统，提供的一种频域的鲁棒控制器设计方法，其最大特点是鲁棒性好［5］。文献［6-8］中通过求解Riccati方程或线性矩阵不等式的不同方法得到系统的状态反馈H∞鲁棒控制器，仿真研究表明，在系统模型不确定及外界扰动作用下，无论模型参数摄动与否，H∞控制器不仅能使系统有很好的鲁棒性，且有很强的抗干扰能力。

为提高光电跟瞄平台的性能，本文采用考虑三轴环架之间的耦合得到的更接近于实际的数学模型作为研究对象，分别设计基于线性矩阵不等式（LMI）的状态反馈H∞控制器和多输入极点配置稳定控制器，以期找到更好的光电跟瞄平台稳定控制设计方法。

1 三轴跟瞄平台数学模型的建立

光电跟瞄平台三轴环架由内到外依次是方位环、俯仰环和横滚环，如图1所示。

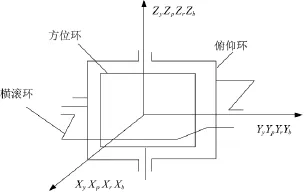
图1 三轴环架结构图

方位环通过方位轴与俯仰环相连，方位环可以绕方位轴相对于俯仰环转动。俯仰环通过俯仰轴与横滚环相连，俯仰环可以绕俯仰轴相对于横滚环转动。横滚环通过横滚轴与基座相连，并可以绕横滚轴相对于基座运动。基座固连在飞机上。伺服电机的电磁转矩直接作用在各环的转轴上，驱动各环转动，调整视轴指向。

考虑环架间的耦合，忽略环架的弹性形变，假设各个环架都是刚体，并假设各环的转轴共点且相邻两轴是严格正交的。据此，以某型跟瞄平台为对象建立坐标系：O-XaYaZa表示惯性坐标系；O-XbYbZb表示与基座固连的坐标系；O-XyYyZy，O-XpYpZp，OXrYrZr分别表示与方位环、俯仰环及横滚环固连的坐标系；定义以下参数：方位环、俯仰环和横滚环的转动角依次为：α、β、γ，三轴转动时，分析得到基座到横滚环，横滚环到俯仰环及俯仰环到方位环的转换矩阵分别为Tbr、Trp和Tpy：

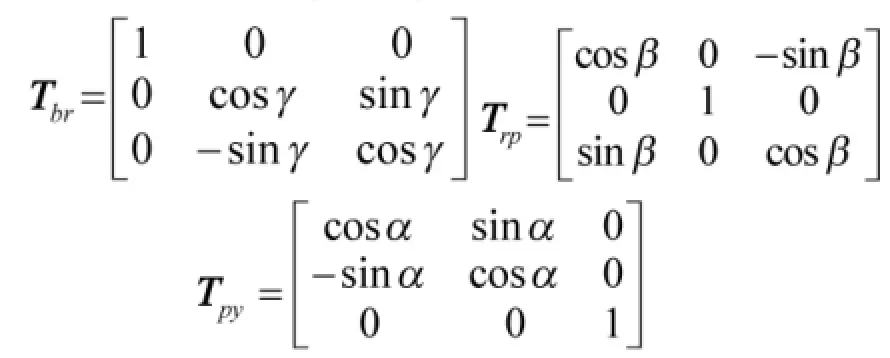
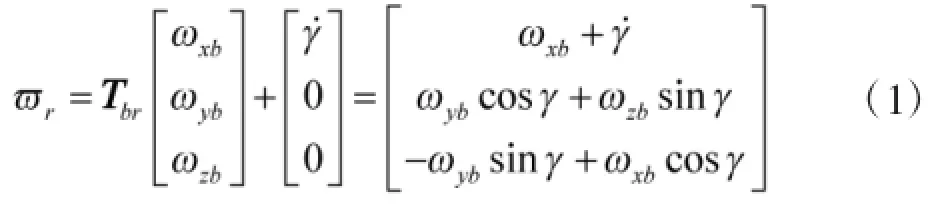
分别为加在方位、俯仰和横滚框架上的外M加力矩。方位环、俯仰环和横滚环的转动惯量在3个坐标轴的分量依次为：JxyJxyJxy，JxpJxpJxp和JxrJxrJxr。

因为方位和俯仰框架是正方形，有Jxy=Jxy=Jxy，Jxp=Jxp=Jxp。依据动量矩定理，得到3个框架的动力学方程分别为：

Mx外是加在横滚框架转动轴上的转动力矩，它等于方位框架、俯仰框架上的转矩在横滚转轴上的投影与横滚框架上外加转矩之和；My中是作用在俯仰框架转动轴上的外加力矩，它等于作用在方位框架的力矩在俯仰轴上的投影与作用在俯仰框架上的外加力矩之和；Mz内为加在方位框架转动轴上的转动力矩，即：

方位环绕自身轴的转角α≤6°，可近似等价于，sinα=α，cosα=1进而可得到环架的动力学方程分别为：

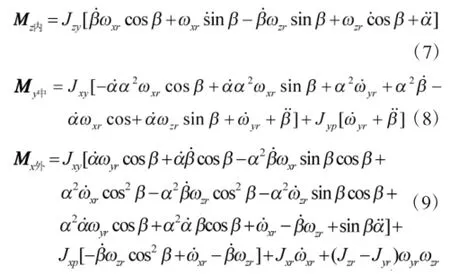
式（7）～式（9）给出的三轴环架数学模型，其方程复杂且是非线性的，不便于控制器的设计和研究，需进行简化和线性化处理。由方位环绕自身轴的转角φ≤6°=0.105 rad为较小量，忽略含有高次较小量的项，在平衡点α=β=γ=0，α.=β.=γ.=0处进行线性化，最后将动力学方程写成矩阵的形式，求得其状态空间方程为：

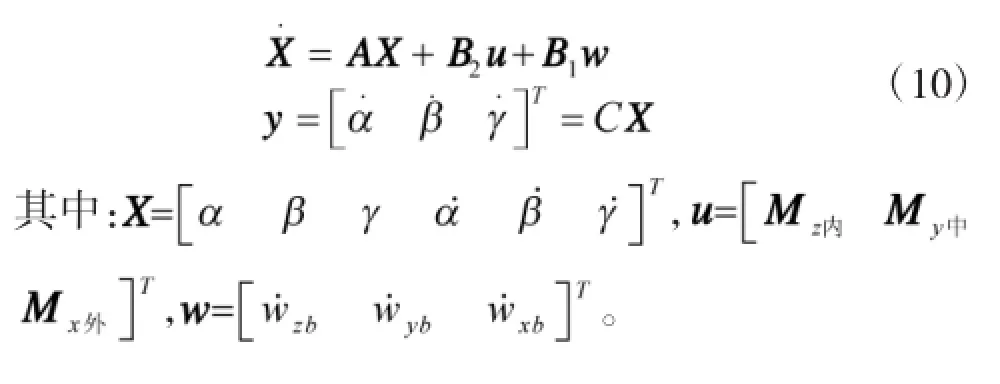
2 状态反馈H∞稳定控制器的设计

光电跟瞄平台的增广被控对象为式（11）：

其中x∈Rn是状态向量，u∈Rm为控制输入，y∈Rp为测量输出，z∈Rr为被控输出，w∈Rq为外部扰动。

设计静态状态反馈控制器u=kx使得相应的闭环系统（12）是渐进稳定的：

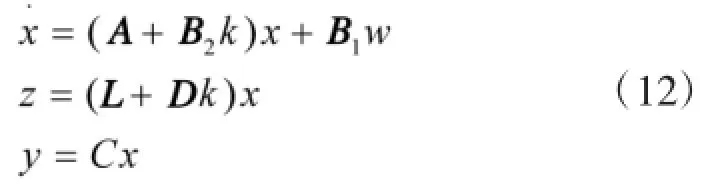
定理［9］：对于系统（11），存在一个状态反馈H∞控制器，当且仅当存在一个对称正定矩阵X和W，使得式（13）的矩阵不等式：

成立，进而，如果矩阵不等式（13）存在一个可行解X和W，那么u=W*X-1x是系统（11）的一个状态反馈H∞控制器。

定义干扰抑制性能指标，令：

利用MATLAB软件包求得可行解X和W，进而得到状态反馈H∞控制器为：

3 极点配置稳定控制器的设计

对式（10）所示的数学模型，不考虑干扰得到光电跟瞄平台的状态空间方程为：

其中B=B2。对式（14）所示系统验证其能控性，可知系统是完全能控的。

从Qc选取6个线性无关向量构造一个线性变换矩阵S-1，将线性系统（14）通过线性变换化为龙伯格能控规范型为：

其中：

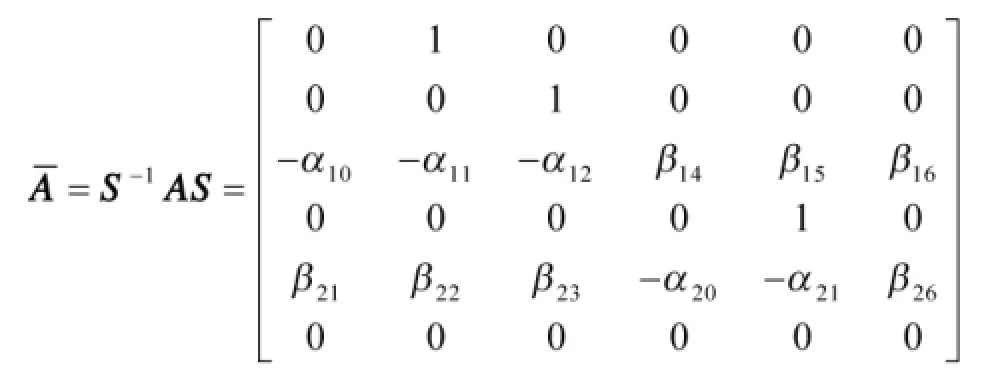
3.1 期望闭环特征根的确定：

综合工程型性能指标，超调量σ=0.4%，上升时间tr=0.6，可得阻尼系数ζ=0.87，时间常数T=0.28，并基此构成一对共轭复数根作为主导极点：

其余4个极点在s左半平面远离主导极点区域选取，具体为：s3=-12，s4，5=-15±j，s6=-14。

将给定的闭环系统期望特征值按照A的对角块阵个数和维数μi（μi为能控性指数，且有（μ1+μ2+…+μi=n，μ1=3，μ2=2，μ1=1））计算相应的特征多项式：

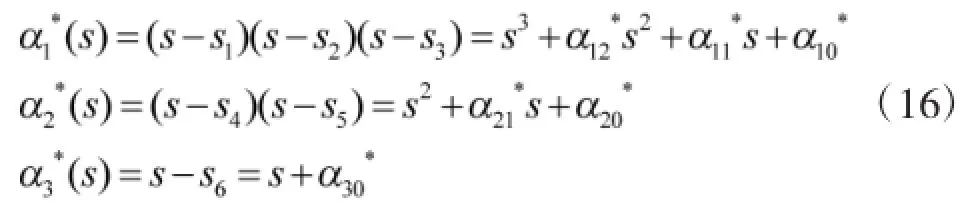
3.2 计算状态反馈矩阵K

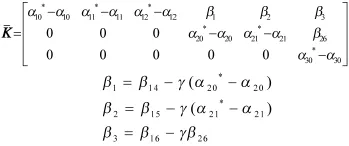
编写MATLAB程序，简化计算，求解得到跟瞄平台稳定控制器。

4 仿真研究

①根据所设计的状态反馈H∞控制器，构造跟瞄平台的稳定控制系统。在方位框架、俯仰框架和横滚框架上分别加幅值为0.05，0.02，0.1的阶跃扰动作为基座角加速度干扰信号，如图2所示。

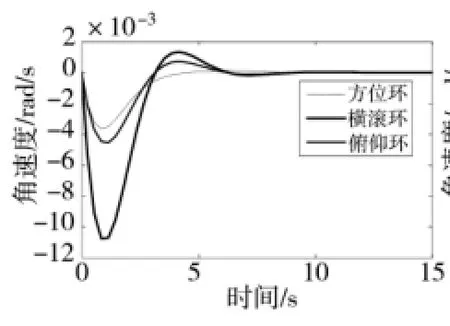
图2 H∞状态反馈稳定控制阶跃扰动响应曲线

图3 极点配置稳定控制阶跃扰动响应曲线

②根据极点配置算法得到的稳定控制器，通过MATLAB编程，构造跟瞄平台的稳定控制系统。加入与①中一样的阶跃扰动，如图3所示。

5 结论

考虑光电跟瞄平台三轴环架间的耦合，建立更接近于实际的数学模型，以此作为研究对象，设计了状态反馈H∞稳定控制器和龙伯格能控规范型极点配置算法稳定控制器。分别构造了两种控制器控制的三轴跟瞄平台稳定控制系统，加入相同条件的阶跃扰动信号，仿真结果显示：二者皆能实现对光电跟瞄平台的稳定控制，都具有一定的鲁棒性能，但H∞控制的超调更小且达到稳定的时间短。同时在设计过程中，基于LMI的状态反馈H∞稳定控制器对系统模型无过多的限制条件，通过求解线性矩阵不等式即可得到控制器；而龙伯格能控规范型极点配置算法较为繁琐，特别对于多输入系统，转化为Loburger规范型的过程更为麻烦。因此，状态反馈H∞控制器更适合于光电跟瞄平台的稳定控制。

［1］卢广山.机载光电跟瞄平台稳定与跟踪控制方法研究［J］.飞机设计，2003，9（3）：38-42.

［2］王连明，葛文奇，谢慕君.陀螺稳定平台速度环的一种神经网络自适应控制［J］.光电工程，2001，28（4）：9-12.

［3］刘珊中，孙隆和.H∞控制在机载光电跟瞄系统中的应用［J］.火力与指挥控制，2007，32（12）：114-117.

［4］MICHELIN J M，COUSTAL P.Control of a sight system flexible structure H∞design［J］.IEEE Proceedings of Decision and control conference，1991，12（4）：1640-1644.

［5］付兴建，童朝南，孙一康，等.H∞控制理论的发展及研究现状［J］.计算技术与自动化，2004，23（1）：25-30.

［6］YANG X B，GAO H J，SHI P，et al.Robust H∞control for a class of uncertain mechanical systems［J］.International Journal of Control，2010，83（7）：1303-1324.

［7］TIAN E G，YUE D，GU Z.Robust H∞control for nonlinear systems over network：A piecewise analysis method［J］.Fuzzy Sets and Systems，2010，161（21）：2731-2745.

［8］GERSHON E，SHAKED U，YESHI.H∞control and filtering of discrete-time sochastic bilinear system［J］.Automation，2001，37（3）：409-417.

［9］俞立.线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.

Stability Controller Design of Electro-optical Tracking and Pointing Platform

LIU Shan-zhong，LI Yan-fan，LIU Yong-bin，QU Xiu-min
（School of Information Engineering，Henan University of Science and Technology，Luoyang 471023，China）

This article is based on the mathematical model which is applying to the design of controller，considering coupling of three-axis frame，respectively design state feedback H∞control based on linear matrix inequality（LMI）and pole assignment stability controller.Set up the two kinds of stability control system of tracking-pointing platform based on the designed controllers，then，the control effect is compared，results showed that，both design could realize stability control，have some robustness. Especially，H∞controller design is much simpler and has a smaller overshoot，time achieving stable is short，witch is more suitable for the stabilization control of electro-optical tracking and pointing system.

electro-optical tracking and pointing system，state feedback H∞control，pole assignment，robustness

V271.4；TP273

A

1002-0640（2016）12-0142-04

2015-10-15

2015-12-26

国家自然科学基金（61203047）；河南省教育厅自然科学研究项目（12A120004）

刘珊中（1968-），女，河南郑州人，博士，教授。研究方向：控制理论与控制工程。