基于加权双曲线定位的DV-Hop改进算法
易仁杰,余剑,吴标,龚阳
(电子工程学院,合肥230037)
基于加权双曲线定位的DV-Hop改进算法
易仁杰,余剑,吴标,龚阳
(电子工程学院,合肥230037)
针对基于双曲线定位的DV-Hop算法中误差项的异方差性引起的定位误差大的问题,提出了一种基于加权双曲线定位的DV-Hop改进算法。算法分析了基于双曲线定位的DV-Hop算法模型中误差项的异方差性,用加权最小二乘法对异方差性进行纠正,对加权最小二乘法中的权值矩阵进行了理论推导并得到与跳数相关的最佳权值矩阵,使得误差项满足同方差性,所得估计值接近最佳线性无偏估计。仿真结果表明,所提算法在定位精度上较目前常见的基于双曲线定位的DV-Hop算法都有一定提高。
异方差,双曲线定位,DV-Hop,加权最小二乘法
0 引言
无线传感器网络[1]是一种由大量的传感节点通过自组织的方式构成的网络,各传感节点集成电源、通信、处理和传感模块,以单跳或多跳的方式进行无线通信,利用自身的存储和计算能力完成整个区域中的信息采集与数据处理。伴随无线通信技术与微机电技术的革新,无线传感器网络技术迅速发展,并被广泛应用到军事、医疗、环境监测、空间探测等领域,深刻地影响着人们的生活[2]。由于节点的位置信息往往至关重要,各国学者针对节点定位技术展开了持续深入的研究。
目前的研究将定位算法分为基于测距[3]和非测距[4]两类。与基于测距的定位算法相比,非测距的定位算法无需直接测距,硬件构成简单,能量消耗低,抗干扰能力较强,同时可以达到一定的精度要求[5]。在基于非测距的定位算法中,DV-Hop[6]算法原理简单、计算量小,硬件实现简单,在节点分布均匀、各向同性的密集型网络中具有较好的定位精度[7],其应用最为成功和广泛。目前针对DV-Hop算法的改进主要集中在待定位节点到锚节点之间距离的求精和根据该距离精确求解待定位节点的位置坐标两方面。针对精确求解待定位节点的位置坐标,文献[8]指出由极大似然估计法所求得的估计值并没有真正满足各误差项的平方和最小,而是各误差项之差的平方和最小,定位精度与参考方程精度有关;对于极大似然估计法存在的不足,文献[9]引入双曲线定位算法,提高了定位精度,但是没有考虑模型中误差项存在的异方差性对最小二乘估计精度的影响;文献[10]在双曲线定位算法的基础上提出加权双曲线定位算法,权值矩阵为待定位节点到锚节点最小跳数的倒数构成的对角阵,在一定程度上消除了模型中误差项的异方差性,降低了定位误差,但是文中未指明该权值矩阵是否为最佳权值矩阵且未见对该权值矩阵进行理论分析。
本文在上述研究的基础上,提出了一种加权双曲线定位的DV-Hop改进算法。算法分析了基于双曲线定位的DV-Hop算法模型中误差项的异方差性,采用加权最小二乘法对异方差性进行纠正,对加权最小二乘法中的最佳权值矩阵进行了理论推导,并根据模型中误差求得与跳数相关的最佳权值矩阵,较好地克服了由误差项的异方差性带来的定位误差大的问题,提高了节点定位精度。
1 DV-Hop算法简介
1.1 算法基本原理
DV-Hop算法的基本原理为:根据网络中节点之间的最小跳数以及锚节点的已知位置信息确定节点的平均每跳距离,之后由跳数与平均每跳距离确定待定位节点与各锚节点之间的距离,最后利用距离信息联立方程求取待定位节点位置坐标。过程如下:
①使用距离矢量交换协议[11],通过各节点间的信息交换求取任意两节点之间的最小跳数。
②计算待定位节点到锚节点的距离。
锚节点的平均每跳距离为:
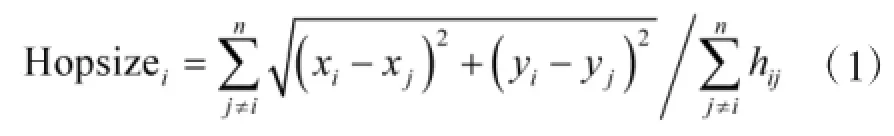
Hopsizei表示锚节点i的平均每跳距离,(xi,yi)表示锚节点i的坐标,(xj,yj)表示锚节点j的坐标,n表示锚节点数目,hij表示锚节点i与j之间的最小跳数。待定位节点u到锚节点i的距离为:

其中dui表示待定位节点u到锚节点i的距离,Hopsizeu表示距离u最近的锚节点的平均每跳距离,hui表示待定位节点u与锚节点i之间的最小跳数。
③三边或多边定位算法定位
根据待定位节点到锚节点的距离可以得到如下方程:
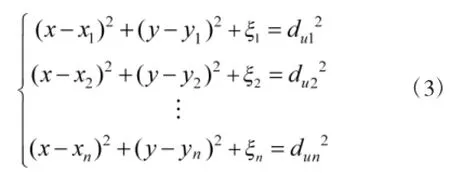
其中(x,y)表示待定位节点坐标,(xi,yi)表示锚节点坐标,ξi表示各距离坐标方程中的观测误差。三边定位算法有针对性地选择3个锚节点进行定位,多边定位算法则利用多个锚节点进行定位,比三边定位算法具有更高的可靠性。目前常见的多边定位采用极大似然估计法,式(3)中各方程通过减去参考方程(此处选择第n个方程作为参考方程)得到线性方程组如下所示:
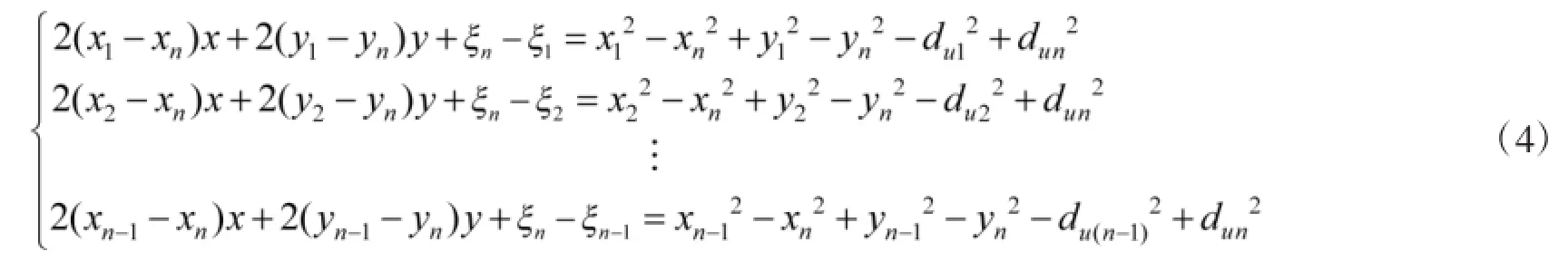
对式(4)采用最小二乘法进行求解定位。然而当ξn较大时,参考方程的精度较低,定位误差明显加大。
1.2 双曲线定位算法
1.2.1 算法基本原理
双曲线定位算法是一种通过将待定位节点定位在以锚节点为焦点、两锚节点之间距离为焦距的双曲线上,根据各双曲线之间的交点确定待定位节点坐标的多边定位算法。文献[9]将双曲线定位用于DV-Hop算法中,获得了比极大似然估计法更高的定位精度,其定位原理如下:
待定位节点u与锚节点i之间的距离为:

假设u到锚节点i的距离与到锚节点j的距离之差为rij,则有rij=dui-duj,u位于以锚节点i和j(j≠i)为焦点、到焦点距离差值为rij的双曲线上。由式(5)可得:
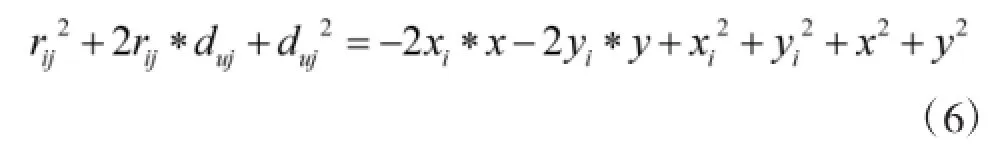
令K=x2+y2,带入误差项后由式(6)可得:
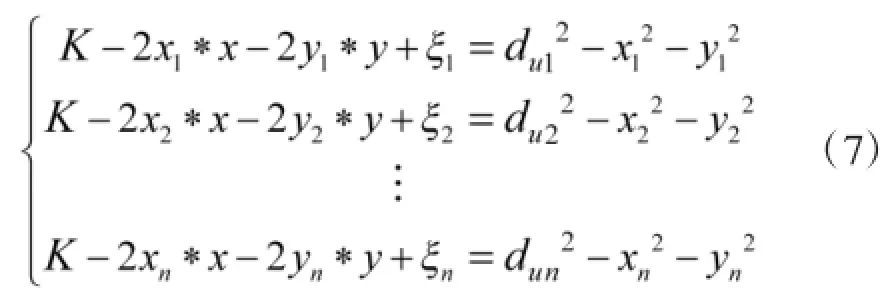
将K、x和y看作未知数,式(7)写成线性方程的形式为:A·c=b,其中:
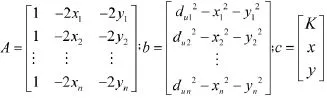
由最小二乘法解得:

待定位节点坐标由式(8)可得:
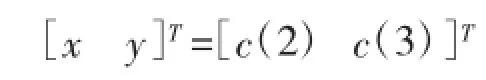
其中c(2)表示列向量c的第2项,c(2)表示列向量c的第3项。
1.2.2 误差项分析
在传感器节点随机均匀分布、忽略环境影响的条件下,可认为观测误差仅与待定位节点和锚节点之间的距离误差有关。假设待定位节点u与锚节点i之间的估计距离与实际距离的误差为Δdui,则Δdui等于u与i最短路径上所有相邻两节点之间的距离在u与i直线方向上的投影与平均每跳距离的误差之和。假设最短路径上相邻两节点之间的距离在该直线方向上的投影与平均每跳距离的误差相互独立且服从零均值同方差的高斯分布,则Δdui均值为零且方差与u、i之间的最小跳数成正比。

由式(9)可知ξi具备零均值、异方差的特性。高斯马尔柯夫定理[12]指出,在给定经典线性回归模型[13]的假定下,最小二乘估计是最佳线性无偏估计。然而误差ξi不满足同方差性,此时经典线性回归模型不成立,最小二乘估计不满足最佳线性无偏估计,需要对误差ξi的异方差性进行纠正,使估计接近最佳线性无偏估计,从而提高定位精度。
2 改进算法
普通的最小二乘法认为每项误差对总体回归直线的偏离程度全部相同,等价于权值都赋为1,各方程可信度[14]相同。然而由于模型中误差项存在异方差性,每项误差对总体回归直线的偏离程度不同,此时普通最小二乘法无法确定各锚节点参与定位的可信度,得到的估计值不满足最优估计,因此,引入加权最小二乘法。
加权最小二乘法的思想是对原模型进行加权,对误差项方差较大的观测值赋予较小的权值,而对误差项方差较小的观测值赋予较大的权值,使之成为一个新的不存在异方差性的模型。根据式(8),加权最小二乘估计的性能指标为:
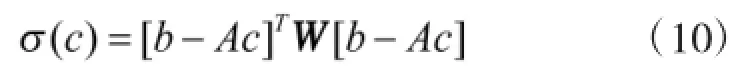
其中σ(c)表示离差平方和,W为正定的权值矩阵。式(10)最小时求得的cLSW为加权最小二乘估计量,此时估计值满足最佳线性无偏估计,对c求偏导得到:
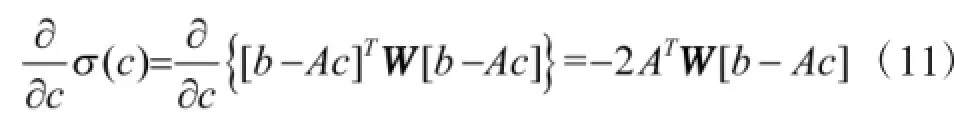
令式(11)为零,得到取极值时坐标:
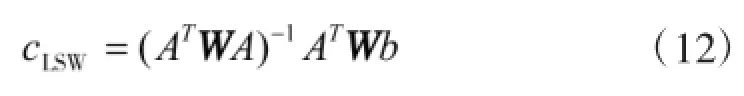
此时估计误差为:

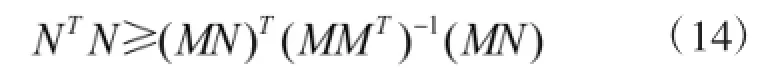
当且仅当存在一个矩阵Q使得N=MTQ时,等式成立。将M和N带入式(14)可得:


当待定位节点u与锚节点i、j不在同一直线上时,u、i之间距离误差Δdui与u、j之间距离误差Δduj相互独立,因此,E{ξiξj}=0。当u与i、j在同一直线上时,由于任意相邻两节点之间的距离在该直线方向上的投影与平均每跳距离的误差相互独立并且方差相同,因此,E{ξiξj}与u、i之间的最短路径跟u、j之间的最短路径的重合段数成正比。而根据网络分布特性可知,u与i、j共线概率极小,认为该重合路径段数在绝大多数情况下为零,因此,忽略B可得:
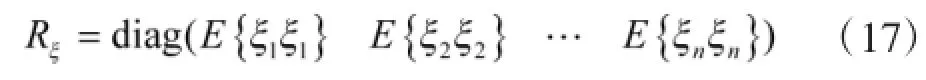
由式(9)可得,
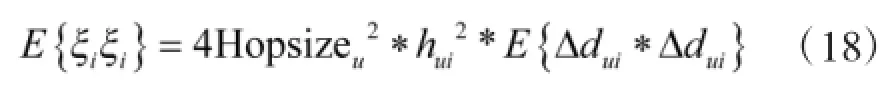
假设相邻节点之间的距离误差的方差为σ2,由于最短路径上任意相邻两节点之间的距离误差相互独立,所以:
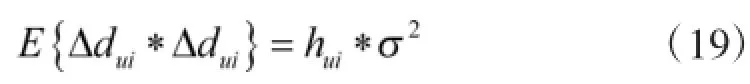
式(8)代入式(19)后,由式(17)可得:
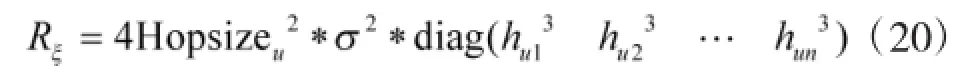
所以权值矩阵化简后为:

将式(21)代入式(12)可求出估计坐标。引入权值矩阵W后,离差平方和为:

其中wi为误差项ξi的权系数,对应于权值矩阵W中对角线上第i个元素,则有:
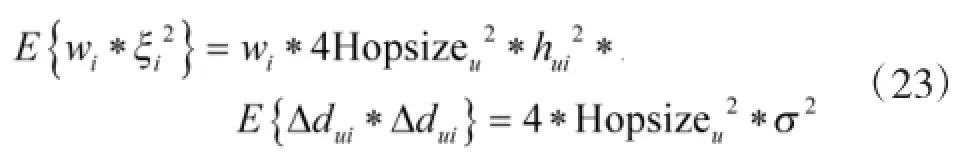
由式(23)可知,引入权值矩阵后,误差项ξi的方差与对应权系数的乘积为与i无关的常数,各误差项在离差平方和中作用相同,方差大的误差项不再具备更高的拟合程度,各误差项对应的拟合程度相当。与文献[10]提出的加权双曲线定位算法相比,权值矩阵不再为待定位节点到锚节点最小跳数的倒数构成的对角阵,而是最小跳数倒数的三次方构成的对角阵,此时异方差性得到明显改善,近似满足最佳线性无偏估计。同时,由于仅增加了待定位节点与锚节点之间最小跳数的立方运算,计算复杂度基本持平。
3 仿真分析
为了对本文提出的算法进行验证,分别对基于双曲线定位的DV-Hop算法、文献[10]提出的加权双曲线算法以及本文所提的改进算法进行仿真。考虑到随机性带来的定位误差,仿真结果取自100次蒙特卡洛[15]仿真的平均值。网络定位误差采用归一化之后的误差,表达式为:
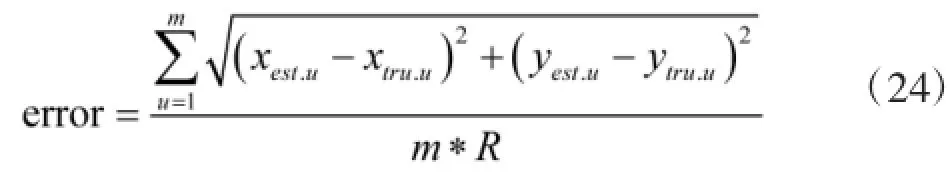
其中m表示未知节点数量,R表示节点通信半径,(xest.u,yest.u)表示待定位节点u的估计坐标,(xtru.u,ytru.u)表示待定位节点的实际坐标。
仿真在Matlab中进行,无线传感器网络环境为:节点随机均匀地分布在边长为100的正方形区域中,节点的通信半径为25,锚节点和待定位节点随机产生,满足均匀分布,其中节点总数、锚节点的比例随着仿真的具体要求而改变。当节点总数为100、锚节点密度为20%时,无线传感器网络节点分布如图1所示,其中“*”表示锚节点,实心圆点表示待定位节点。

图1 节点分布示意图
实验1特定情况下算法的定位性能比较
在节点总数为100、锚节点密度为20%的条件下进行仿真,基于双曲线定位的DV-Hop算法、文献[10]中的算法以及本文改进算法的定位效果分别如图2(a)、图2(b)、图2(c)所示,其中空心圆点表示待定位节点的估计坐标。未知节点的实际位置与估计位置由线段连接,线段越长表示定位误差越大。图2(d)为100次蒙特卡洛仿真取均值求得3种算法的定位效果对比图,横坐标表示待定位节点标号,纵坐标表示相应的待定位节点的平均定位误差。从图2(d)中可以看出,基于双曲线定位的DV-Hop算法、文献[10]提出的改进算法以及本文改进算法的定位误差依次为30%、26%、23%,本文算法的定位误差较前两种算法均有所降低。
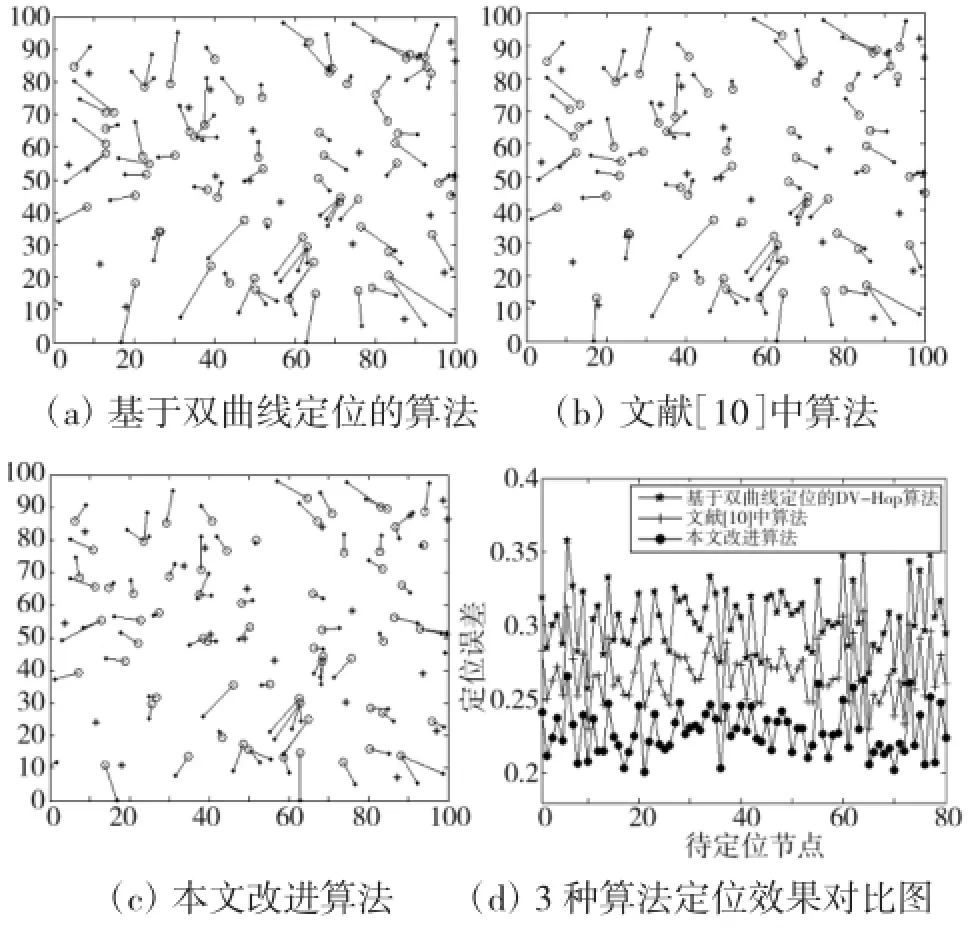
图2 算法定位效果图
实验2不同节点数量情况下算法的定位性能比较
假设锚节点密度为20%,在节点总数不同的情况下分别比较本文改进算法与传统双曲线定位算法以及文献[10]中算法之间的定位性能,得到仿真结果如图3所示。图中横坐标表示网络中节点总数,纵坐标表示归一化之后的网络定位误差。随着网络中节点总数的增加,网络的连通性增强,锚节点平均每跳距离更加精确,未知节点与锚节点之间的距离估算值更加接近真实值,3种算法定位误差均减小并最终趋于稳定。由于克服了模型中误差项的异方差性对定位的影响,在相同条件下本文改进算法的网络定位误差比基于双曲线定位的DV-Hop算法降低约7%,比文献[10]中的算法降低约4%。
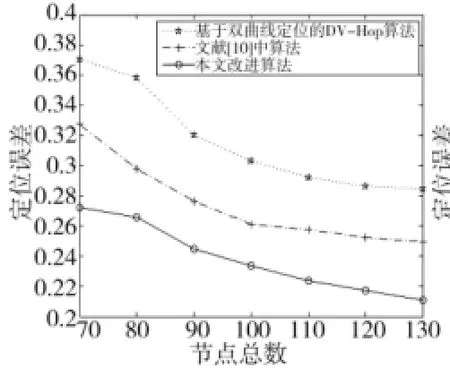
图3 节点数量与定位误差的关系
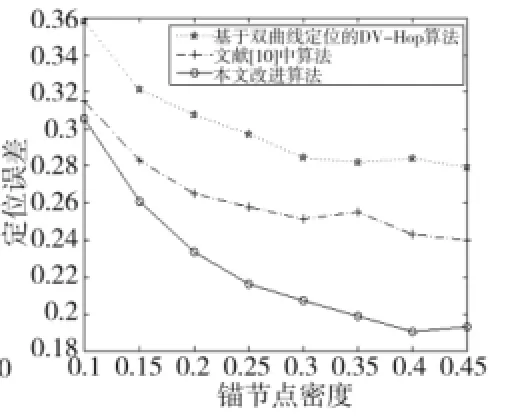
图4 锚节点密度与定位误差的关系
实验3不同锚节点密度情况下算法的定位性能比较
假设节点总数为100,在锚节点密度不同的情况下分别比较本文改进算法与传统双曲线定位算法以及文献[10]中算法之间的定位性能,得到仿真结果如图4所示。图中横坐标表示网络中锚节点密度,纵坐标表示归一化之后的网络定位误差。在节点总数保持不变的情况下,随着锚节点密度的增加,参与定位的锚节点数量增加,3种算法的定位误差逐渐降低,本文所提算法定位误差逐渐降低并最终趋于稳定。在锚节点密度为45%时,本文改进算法网络定位误差为19.3%,比基于双曲线定位的DV-Hop算法降低大约8.6%,比文献[10]中改进算法降低约4.7%。
4 结论
本文介绍了传统的基于双曲线定位的DV-Hop算法并分析了误差项的异方差性,针对由异方差性引起的定位误差大的问题,提出了一种基于加权双曲线定位的DV-Hop改进算法。算法根据网络中节点间距离误差与跳数之间的关系,对最佳权值矩阵进行了理论推导,得到了仅与节点间跳数相关的权值矩阵,纠正了传统算法中误差项的异方差性,使改进之后的加权最小二乘估计接近最佳线性无偏估计。仿真结果表明,与传统的基于双曲线定位的DV-Hop算法及文献[10]中的算法相比,本文改进算法具有更高的定位精度。
[1]AKYILDIZ I F,SU W,SANKARASU Y,et al.Wireless sensor networks:a survey[J].Computer Networks,2002,38(4):393-422.
[2]ARAMPATZIS T,LYGEROS J,MANESIS S.A survey of applications of wireless sensors and wireless sensor networks[C]//Intelligent Control,2005.Proceedings of the 2005 IEEE InternationalSymposiumon,MediterreanConferenceon Control and Automation.IEEE,2005:719-724.
[3]BOUSHABA M,HAFID A,BENSLIMANE A.High accuracy localization method using AoA in sensor networks[J].Computer Networks,2009,53(18):3076-3088.
[4]CHEN M X,WANG Y D.An efficient location tracking structure for wireless sensor networks[J].Computer Communications,2009,32(13):1495-1504.
[5]JIAN L,HE P L.A new weighted centroid localization algorithm in coal mine wireless sensor networks[C]//Computer Research and Development(ICCRD),2011 3rd International Conference on.IEEE,2011,3:106-109.
[6]NICULESCU D,NATH B.DV based positioning in ad hoc networks[J].Telecommunication Systems,2003,22(4):267-280.
[7]邱奉美,游晓鹏,李怀忠.几种无需测距定位算法定位性能仿真研究[J].计算机仿真,2014,31(4):285-289.
[8]钟丽鸿,胡成全,金京姬.基于RSSI极大似然估计定位算法的分析与实现[J].吉林大学学报(理学版),2014,52(3):556-560.
[9]CHEN H,SEZAKI K,DENG P,et al.An improved DV-Hop localization algorithm for wireless sensor networks[C]//Industrial Electronics and Applications,2008.ICIEA 2008.3rd IEEE Conference on.IEEE,2008:1557-1561.
[10]吴玉成,李江雯.基于最优节点通信半径的改进DV-Hop定位算法[J].华南理工大学学报(自然科学版),2012,40(6):35-42.
[11]BULUSU N,HEIDEMANN J,ESTRIN D.GPS-less lowcost out-door localization for very small devices[T].IEEE Personal Communications,2000,7(5):28-34.
[12]倪伟才.高斯马尔柯夫定理的拉格朗日证明方法[J].统计与决策,2009,25(2):153-153.
[13]何晓群,刘文卿.浅谈加权最小二乘法及其残差图——兼答孙小素副教授[J].统计研究,2006,23(4),53-57.
[14]CHUAN X.Research on improved DV-HOP localization algorithm based on weighted least square method[C]//Knowledge Acquisition and Modeling Workshop,2008.KAM Workshop 2008.IEEE International Symposium on.IEEE,2008:773-776.
[15]邵伟.蒙特卡洛方法及在一些统计模型中的应用[D].济南:山东大学,2012.
An Improved DV-Hop Algorithm Based on Weighted Hyperbolic Positioning
YI Ren-jie,YU Jian,WU Biao,GONG Yang
(Electronic Engineering Institute,Hefei 230037,China)
Aiming at solving the problem that the heteroscedasticity of observation errors leads to low locating accuracy in DV-Hop algorithm which is based on hyperbolic positioning,this paper proposes an improved DV-Hop algorithm which is based on weighted hyperbolic positioning.The algorithm analyzes the heteroscedasticity of the error term in the model and takes advantage of weighted least square method which corrects heteroscedasticity straightforwardly.Then,the weight matrix that is related to least hops between nodes is deduced,the estimators thus obtained are more close to the best linear unbiased estimator.The simulation results show that the localization performance of the improved algorithm is better than the current DV-Hop algorithm.
heteroscedasticity,hyperbolic positioning,DV-Hop,weighted least square method
TP212
A
1002-0640(2016)12-0096-05
2015-10-11
2015-12-19
易仁杰(1990-),男,湖北随州人,硕士研究生。研究方向:无线传感器网络。

